Revisiting Heterophily For Graph Neural Networks
概
介绍了一种新的 graph homophily metrics.
符号说明
- \(\mathcal{G} = (\mathcal{V}, \mathcal{E}, A)\), graph;
- \(|\mathcal{V}| = N\);
- \(A \in \mathbb{R}^{N \times N}\), adjacency matrix;
- \(\mathcal{N}_i = \{j: e_{ij} \in \mathcal{E}\}\), neighborhood set;
- \(X \in \mathbb{R}^{N \times F}\), feature matrix;
- \(Z \in \mathbb{R}^{N \times C}\), label encoding matrix, 每一行是一个 ont-hot 向量.
Homophily metrics
-
Edge homophily: 每条边两端的结点的类别的一致性,
\[ H_{edge}(\mathcal{G}) = \frac{ |\{ e_{uv} | e_{uv} \in \mathcal{E}, Z_{u,:} = Z_{v,:} \}| }{ |\mathcal{E}| }. \] -
Node homophily: 每个结点和它的邻居结点的类别的一致性 (使用最多的一个指标),
\[ H_{node}(\mathcal{G}) = \frac{1}{|\mathcal{V}|} \sum_{v \in \mathcal{V}} H_{node}^v, \quad H_{node}^v = \frac{ |\{ u| u \in \mathcal{N}_v, Z_{u,:} = Z_{v,:} \}| }{ d_{v} }. \]其中 \(d_v = |\mathcal{N}_v|\).
-
Class homophily: 它主要是用于解决 imbalanced classes 之前的 metrics 可能会过大的问题,
\[ H_{class}(\mathcal{G}) = \frac{1}{C-1} \sum_{k=1}^C \bigg[ h_k - \frac{ |\{v| Z_{v, k} = 1\} }{N} \bigg]_+, \\ h_k = \frac{ \sum_{v \in \mathcal{V}} | \{ u|Z_{v, k} = 1, u \in \mathcal{N}_v, Z_{u,:} = Z_{v,:} \} | }{ \sum_{v \in \{v|Z_{v,k}=1\}} d_{v} }, \]其中 \([a]_+ := \max(a, 0)\).
-
上述的 metrics 的取值范围都为 [0, 1], 越大表明越强的 homophily. 但是作者认为, 这些指标难以准确的显示一个图的可判别性, 如下图所示的简单的二部图的情况:
-
这种情况下, 它们的 homohily metrics 都是 0, 但是即便如此, 应该 Aggregation 后, 它们依旧能够无碍地进行区分. 换言之, 上述地 homohily metrics 和图结点的可判别性并不是直接挂钩的. 作者希望用一个更加合适的 metric 来替代.
Post-aggregation node similarity matrix
-
让我们首先考虑用 SGC 来进行结点预测的方式:
\[ Y = \text{softmax}(Y') = \text{softmax}(\hat{A}XW), \]其中 \(W\) 是通过如下的损失进行训练的:
\[ \mathcal{L} = -\text{Tr}(Z^T \log Y). \] -
作者证明, 倘若采用学习率为 \(\gamma\) 的一般的梯度下降训练, 有
\[\Delta Y' = \hat{AX \Delta W} = \gamma \hat{A}X \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} W} \propto \hat{A}X \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} W} = \underbrace{\hat{A}XX^T\hat{A}^T}_{=: S(\hat{A}, X)} (Z - Y). \]
注: 作者证明的时候把 softmax 转换为:
然后进行矩阵推导的方式挺巧妙的. 但是在推导的时候,
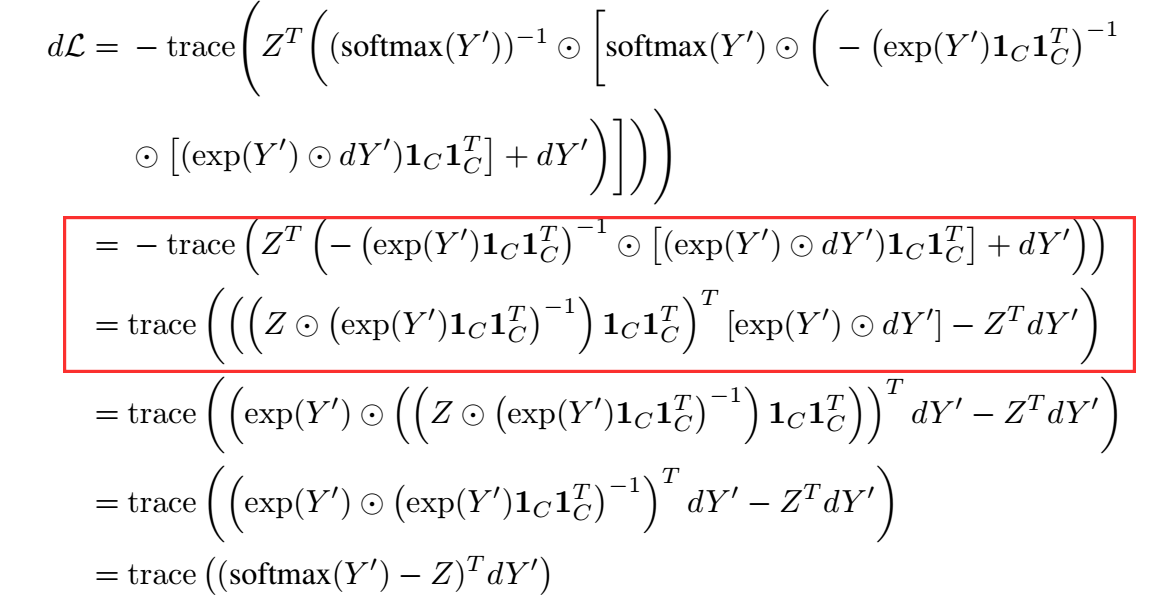
红色框出的部分, 我不知道是怎么来的. 无论是手推还是用数值计算得出的结果都是不等的. 不知道是我理解错了, 还是作者的证明有些瑕疵.
-
总而言之, 作者认为 \(S(\hat{A}, X)\) 能够更好地反映 aggregation 后的 heterophily, 进一步, 作者定义 aggregation similarity score:
\[S_{agg}(S(\hat{A}, X)) = \frac{1}{|\mathcal{V}|} \bigg| \bigg\{ v| \text{Mean}( \{ S(\hat{A}, X)_{v, u} | Z_{u,:} = Z_{v,:} \ge S(\hat{A}, X)_{v, u} | Z_{u,:} \not= Z_{v,:} \} ) \bigg\} \bigg|. \] -
这种情况下得到的指标往往是 \(\ge 0.5\) 的, 为了和上面的指标保持一致, 作者又稍微做了一些改进
\[ S_{agg}^M (S(\hat{A}, X)) = [ 2 S_{agg}(S(\hat{A}, X)) - 1 ]_+. \]
代码
[official]
