Coding

目录

Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition)

Coding Redundancy

假设一个图片\(f(x, y)\)其大小为\(M \times N\), 我们可以估计其密度函数:

\[p_r (r_k) = \frac{n_k}{MN}, \quad k=0, 1, 2,\cdots, L-1, \]

即一个像素点为\(r_k\)的概率为\(p_r(r_k)\).
若对于每个\(r_k\)我们采用\(l(r_k)\)bits来表示, 则平均每个像素点需要:

\[L_{\mathrm{avg}} = \sum_{k=0}^{L-1} l(r_k)p_r(r_k). \]

最普通的, 如果\(L=256\), \(l(r_k)=8\), 即我们采用8bits的量来表示. 为什么对不同的\(r_k\)采取不同的表示, 这是由于我们往往可以找到一个编码使得可以采用更少的空间来表示实现数据压缩(无损或者有损).

Huffman Coding

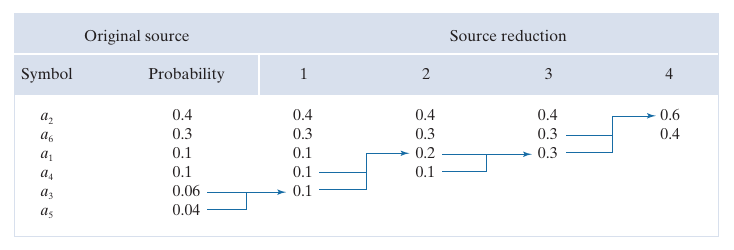
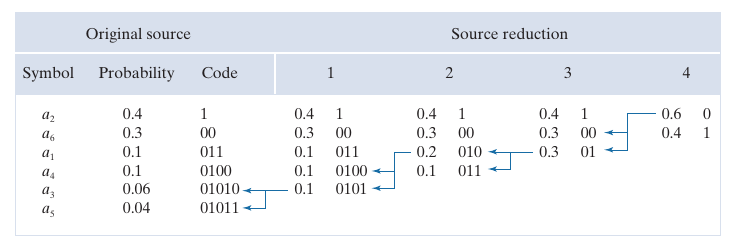
如上图所示, 假设共有\(a_1, a_2,\cdots, a_6\)这六种密度值, 按照概率从高到低排列. 首先从低到高, 逐步合并最低的两项直到只剩下两项(0.6, 0.4). 分别赋予\(0, 1\), 由于\(0.6\)是由前面的\(0.3, 0.3\)合并而成, 对其分裂, 在其原有编码的基础上分裂出\(00, 01\), 重复进行.

from bitarray import bitarray

def huffman(dist: dict):
    items = sorted(dist.items(), key=lambda t: (t[1], t[0]), reverse=True)
    assert len(items) != 0, "Empty data received ..."
    if len(items) <= 2:
        lt = dict(items)
        lt[items[0][0]] = bitarray('0')
        try:
            lt[items[1][0]] = bitarray('1')
        except KeyError:
            pass
    else:
        dist_reduced = dict(items[:-2])
        dist_reduced[items[-2][0]] = items[-2][1] + items[-1][1]
        lt = huffman(dist_reduced)
        lt[items[-1][0]] = lt[items[-2][0]]
        lt[items[-2][0]] += bitarray('0')
        lt[items[-1][0]] += bitarray('1')
    return lt

显然, 通过这种方式, 我们可以用更少的空间保存数据, 但是需要注意的是, 这种方式有额外的开销, 我们需要建立一个由 新编码 到 symbol 之间的一个映射关系.

另外, 可能会有疑问, 如果用:

\[\tag{x} 0, 1, 00, 01, 10, 11 \]

这种方式编码不是更简单? 实际上, 在实际保存的时候, 是一连串的编码, 如:

\[010100111100, \]

按照上面, 实际上是

\[a_3a_1a_2a_2a_6, \]

但是(x)的编码是不能区分的, 比如\(00\)无法区分是两个\(0\)还是一个单纯的\(00\), 但是可以发现, huffman编码在这种情况下依旧是能够唯一确定的.

Golomb Coding

记\(\lceil x \rceil\)为大于等于\(x\)的最小整数, \(\lfloor x \rfloor\)为小于等于\(x\)的最大整数, 非负整数\(n\)的编码\(G_m(n)\)为:

  1. \(k = \lfloor n/m \rfloor\), 则其unary code定义为:

\[\underbrace{11\cdots11}_{k} 0; \]

  1. \(k = \lceil \log_2 m \rceil\), \(c=2^k - m, r=n\: \mathrm{mod}\: m\), 计算:

\[r' = \left \{ \begin{array}{cc} r \: \text{truncated to} \: k-1 \: \text{bits} & 0 \le r < c \\ r + c \: \text{truncated to} \: k \: \text{bits} & \text{otherwise} \end{array} \right . \]

  1. 将上面两步所得首尾相连.

举个例子, \(G_4(9)\), 第一步算出来为:

\[110, \]

第二步\(k=2, c=0, r=1\), 故\(r+c=1=(0001)_2\),

\[r' = (01)_2. \]

故

\[G_4(9) = 11001. \]

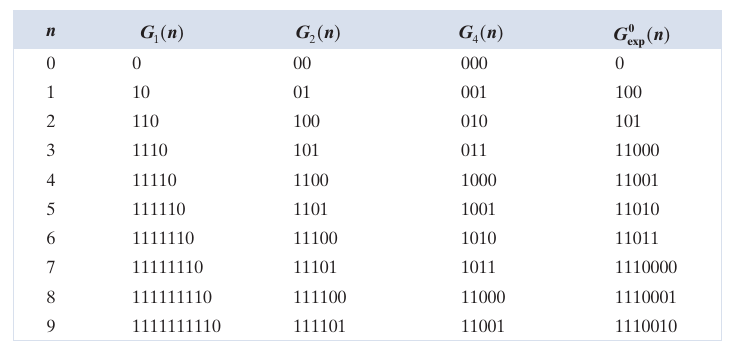
如上图所示, 还有一种特殊的\(G_{\mathrm{exp}}^k(n)\)的编码, 其是一种更具广泛性的编码, 具体步骤如下:

  1. 找到\(i\)满足:

\[\sum_{j=0}^{i-1} 2^{j+k} \le n < \sum_{j=0}^i 2^{j+k}, \]

计算\(i\)的unary code;
2. 将

\[n - \sum_{j=0}^{i-1}2^{j+k} \]

截断为\(k+i\)bits.
3. 连接上面两步的结果.

比如\(G_{\exp}^0(8)\), \(k=0\), 则\(i=3\), 其unary code为\(1110\), \(8-\sum_{j=0}^{2}2^{j+0}=8-7=(0001)_2\), 保留为\((001)_2\), 故最后结果为:

\[(1110001)_2. \]

import math
from bitarray import bitarray

def golomb(n: int, m: int):
    """
    >>> golomb(9, 4)
    bitarray('11001')
    """
    assert n >= 0, "Postive interger required ..."
    part1 = bitarray('1' * (n // m) + '0')
    k = math.ceil(math.log(m, 2))
    c = 2 ** k - m
    r = n % m
    if r < c:
        part2 =  bitarray('0') * k + bitarray(bin(r)[2:])
        part2 = part2[-k+1:]
    else:
        part2 = bitarray('0') * k + bitarray(bin(r+c)[2:])
        part2 = part2[-k:]
    return part1 + part2


def golomb_exp(n: int, k: int = 0):
    """
    >>> golomb_exp(8)
    bitarray('1110001')
    """
    i = math.floor(math.log(n * 2 ** (-k) + 1, 2))
    part1 = bitarray('1' * i + '0')
    part2 = bitarray('0') * (k + i) \
            + bitarray(bin(n - 2 ** k * (2 ** i - 1))[2:])
    part2 = part2[-k-i:]
    return part1 + part2

Arithmetic Coding

就是用一个有限小数来表示一个序列, 比如序列\(a_1a_2a_3a_3a_4\), 有四个symbol, 首先计算四个symbol对于的概率(频率), 分别是

\[0.2, 0.2, 0.4, 0.2, \]

则定义各自的初始区间为:

然后按照下列流程划分:

首先, 由于第一个symbol是\(a_1\), 故最后的编码的结果是落在\([0, 0.2)\)中的, 再将\([0, 0.2)\)按照上面的情况类似的划分, 又由于第二个symbol是\(a_2\), 最后编码的结果是落在第二个区间\([0.04, 0.08)\). 重复进行, 知道最后一个symbol, 发现最后编码的结果落在\([0.06752, 0.0688)\), 此时我们选取此区间中任意一个数来表示整个序列, 当然最好是位数少这样转成二进制所消耗的存储空间也会小一点, 比如这里可以选择\(0.068\).

from typing import List
import numpy as np

def arithmetic(seq: List) -> float:
    indices = {key: idx for idx, key in enumerate(set(seq))}
    marks = np.cumsum([0] + [seq.count(key) for key in indices.keys()]) / len(seq)
    l, r = 0, 1
    for item in seq:
        idx = indices[item]
        l, r = l + (r - l) * marks[idx], l + (r - l) * marks[idx + 1]
    return (l + r) / 2

想要decode, 我们需要一个额外的字典, 记录symbol和对应的区间(序)以及总共的长度, 每一次我们需要判断数落在哪个区间, 以判断是哪个symbol.

# s
def half_split(x, arr):
    l, r = 0, len(arr)
    while l < r:
        m = (l + r) // 2
        item = arr[m]
        if x <= item:
            r = m
        else:
            l = m + 1
    return l


def iarithmetic(code: float, length: int, keys: List, marks: List):
    l, r = 0, 1
    seq = []
    for _ in range(length):
        idx = half_split((code - l) / (r - l), marks) - 1
        seq.append(keys[idx])
        l, r = l + (r - l) * marks[idx], l + (r - l) * marks[idx + 1]
    return seq

# print(
#     iarithmetic(
#         0.068,
#         5,
#         [1, 2, 3, 4],
#         marks=[0, 0.2, 0.4, 0.8, 1]
#     )
# )
# output: [1, 2, 3, 3, 4]

LZW Coding

Lempel-Ziv-Welch coding: GIF, TIFF, PDF.

  1. 首先构建一基本的字典, 比如key: 0-255 对应symbol\(a_0, a_1, \cdots, a_{255}\);
  2. 欲编码序列\(c_0c_1\cdots\);
  3. 从\(c_0\)开始, 倘若\(c_0\)在基本的字典中, 则令\(P=c_0\), 否则扩展字典, 比如令256表示\(c_0\)以及输出编码256. 若\(c_0\)在基本的字典中, 下一步到\(c_1\), 此时考察\(c_0c_1\), 若其不在基本的字典中, 则扩展字典并输出\(c_0\)对应的key.
  4. 如此往复

感觉代码写的不是很清楚, 还是来一个实际的例子比较好:

\[39, 39, 126, 126, \\ 39, 39, 126, 126, \\ 39, 39, 126, 126, \\ 39, 39, 126, 126. \]

假设要对上面的序列进行编码, 步骤如下:

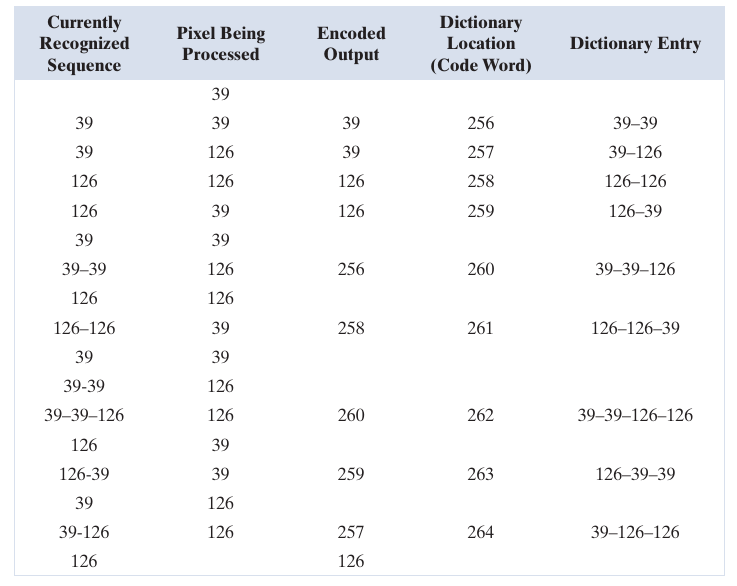
首先我们定义基本的字典\(d\), 且\(d[k] = k, k=0,1,\cdots, 255\), 即预定义\(0-255\)对应的值. 由于第一个值是\(39\), 其属于基本的字典中, 故令\(P=39\), 下一步要考察39-39, 显然不在字典中, 故令\(d[256] = \text{39-39}\), 并输出第一个编码\(39\)代表第一个39被编码为39, 现在\(P=39\). 此时考察39-126, 同样地, 因为其不属于字典, 故\(d[257] = \text{39-126}\)并输出39. 实际上对于头四个数字, 其编码为\(39, 39, 126, 126\), 且需要额外扩充字典

\[d[256] = \text{39-39} \\ d[257] = \text{39-126} \\ d[258] = \text{126-126} \\ d[259] = \text{126-39}, \]

此时\(P=\text{39}\), 此时需要处理39-39, 但是由于39-39已经在字典中了, 故\(P=\text{39-39}\), 此时考察39-39-126, 由于其不在字典中, 扩充字典

\[d[260] = \text{39-39-126}, \]

并输出39-39的编码256, 并令\(P=126\).
不断重复.

一个好处是, 我们不需要记录扩展的表, 通过基本的表我们就可以解码, 具体论述会比较麻烦, 还是用例子来说明比较好. [39, 39, 126, 126, 39, 39, 126, 126]编码后为[39, 39, 126, 126, 256, 258].

解码过程:

  1. 39在字典中, 故解码出的结果为39, 记录\(P=39\);
  2. 39在字典中, 故解码出的结果为39, 同时39-39不在字典中, 扩展字典\(d[256] = \text{39-39}\), 且\(P=39\);
  3. 对于126, 126一样, 记录\(d[257] = \text{39-126}, d[258] = \text{126-126}\);
  4. 现在\(P=126\), 需要处理256， 其编码结果为39-39, 判断\(\text{P-39}\)是否在字典中, 不在, 故扩展\(d[259]=\text{126-39}\), 令\(P=\text{39-39}\);
  5. 处理\(258\), 其编码结果为126-126, 此时需要判断\(\text{P-126}\)是否在字典中, 不在, 故扩展$d[260] = \text{39-39-126}.
  6. ...

显然这就是一个便解码便扩展字典的过程, 具体代码可以参考下面, 会发现解码的部分会稍显复杂, 因为解码的时候还需要考虑一种额外的特殊情况.

from typing import Iterable, Optional, Tuple, Union, List

class LZW:

    def __init__(self, basic: Optional[List] = None):

        if basic is None:
            basic = list(range(255))
        self.basic = basic

     
    def forward(self, seq: Iterable):
        keys = list(map(str, self.basic))
        codebook = {keys[k]:k for k in range(len(keys))}
        P = ''
        encoded = []
        for item in seq:
            item = str(item)
            if P + item in keys:
                P = P + item
            else:
                encoded.append(codebook[P])
                keys.append(P + item)
                codebook[P + item] = len(keys)
                P = item
        encoded.append(codebook[P])
        return encoded

    def backward(self, seq: Iterable):
        keys = list(map(str, self.basic))
        codebook = {k:[keys[k]] for k in range(len(keys))}
        P = []
        decoded = []
        for code in seq:
            print(P, code)
            try:
                first = codebook[code][0]
            except KeyError:
                first = P[0]
            condition = ''.join(P + [first])
            if condition not in keys:
                keys.append(condition)
                codebook[len(keys)] = P + [first]
            item = codebook[code]
            P = item
            decoded += item
        return decoded

Run-Length Coding

CCITT, JBIG2, JPEG, M-JPEG, MPEG-1,2,4, BMP.

图片等序列元素间往往存在关联, 呈现间断连续的情况, 如\(3, 3, 3, 3, 5, 5, 5\), 此时我们可以用\((3, 4), (5, 3)\)来表示. 这种编码方式在binary序列中格外有效, 因为比如\(0, 0, 0, 0, 1, 1, 1\), 可以编码为\(4, 3\)(假设首项目为\(0\), 否则\(0, 4, 3\)).

书上还有关于CCITT的介绍, 但是这部分内容, 即为什么这个编码方式能够奏效不是很理解, 这里就不记录了.


from typing import List, Iterable

class RunLength:

    def __init__(self, first: int = 0):
        self.first = first
    
    def forward(self, seq: Iterable) -> List:
        P = self.first
        count = 0
        encoded = []
        for item in seq:
            if item is not P:
                encoded.append(count)
                P = item
                count = 1
            else:
                count += 1
        encoded.append(count)
        return encoded
    
    def backward(self, seq: Iterable) -> List:
        def generation(first):
            p = 1 - first
            while True:
                p = 1 - p
                yield p

        P = generation(self.first)
        decoded = []
        for code in seq:
            decoded += [next(P)] * code
        return decoded

Symbol-Based Coding

JBIG2

首先, 通过构建一些常用的symbols, 对于序列, 利用

\[\{(x_1, y_1, t_1), (x_2, y_2, t_2), \cdots\} \]

来表示. 其中, \((x_i, y_i)\)表示symbol在序列中的位置, 而\(t_i\)表示是symbol在字典中的位置.

如:

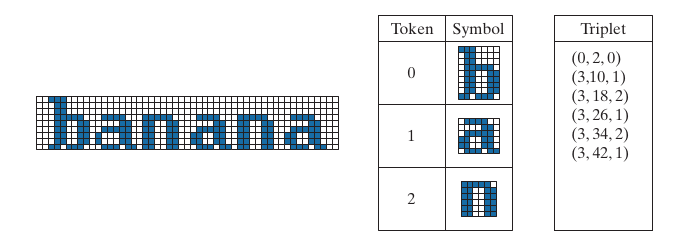
将'b', 'a', 'n'作为symbols, 而\((x_i, y_i)\)记录了每个symbol左上角元素的位置. 显然当symbols的重复利用率比较高的时候, 这种方式是非常节约空间的, 这种编码方式在文档存储中会有比较大的利用空间.

Bit-Plane Coding

JBIG2, JPEG-2000.

之前提到的多种方法都是适用于binary元素的, 那么如RGB图片, 采用8bits的如何利用先前的方法呢? 注意到, 我们可以将任意的mbits (0-\(2^m-1\)), 转换成:

\[a_{m-1}2^{m-1} + a_{m-2}2^{m-2} + \cdots + a_12 + a_02^0. \]

\(a_i \in \{0, 1\}\), 故对于每一个bit plane (共m个bit plane), 我们可以利用先前的方法进行压缩.

Block Transform Coding

JPEG, M-JPEG, MPEG-1,2,4, H.261, H.262, DV, HDV, VC-1.

这是将原图切割成不重叠的子图, 然后分块处理的编码方式, 具体流程如下:

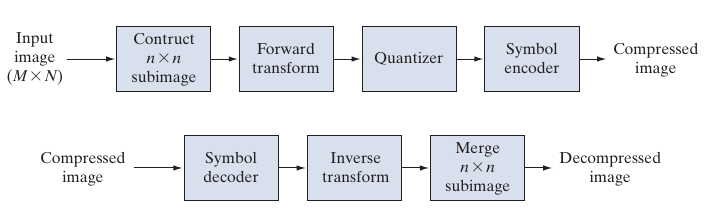
Transform Selection

之前提到过的, DFT, WHT, DCT等都可以, 其中DCT较为常用(因为其连续性).一般使用DCT.

Subimage Size Selection

好的size, 需要保证Subimages之间的关联性不是很强, 通常的选择是\(8\times 8, 16 \times 16\).

Bit Allocation

为了更好地分配bits的使用, 有zonal coding 和 thresholding coding.

假设\(I_k\)为第\(k\)个子图, 而\(\sigma_n^2\)表示通过\(I_k, k=0,1,\cdots\)计算的第\(n\)各元素的方差, 通常, 方差越大表示该位置的信息表示越复杂, 故该位置的信息愈要保留下来.

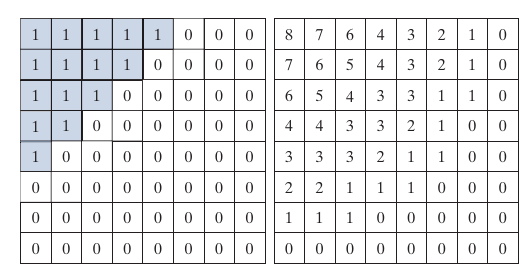
如上图所示, 左图表示zonal mask, 1表示该位置的信息保留, 右边是bits的分配, 如8表示用8bits来表示.

threshold coding则更为简单粗暴:

  1. 所有子图的小于某个值的元素都归0;
  2. 对每个子图设定不同的阈值;
  3. 阈值是不同位置不同子图的函数.

第三种, 通常如下:

\[\hat{T}(u, v) = \mathrm{round}[\frac{T(u, v)}{z(u, v)}], \]

这里\(Z\)是给定的用于量化的值. 显然这种方式能够让\(\hat{T}\)的值进一步趋同.

通过上图可以发现, mask后的值通常沿着对角线趋于0, 故实际通常采用zigzag的排列方式对二维序列重排, 是的有更长的0元.

JPEG

JPEG的流程如下(8bits):

  1. 每个元素减去\(2^7\);
  2. DCT;
  3. 通过量表量化:

\[\hat{T}(u, v) = \mathrm{round}[\frac{T(u, v)}{Z(u, v)}]. \]

  1. 对零处进行处理分组, 并根据标准码表编码, 以及用哈夫曼编码零的统计数字.

Arvin_JIN 的博客里讲得很清楚, 区别是\(-2^7\)变成了转成YCbCr格式.

Predictive Coding

对于序列\(f(n)\), 实际上编码

\[e(n) = f(n) - \hat{f}(n), \\ \hat{f}(n) = \mathrm{round}[\sum_{i=1}^m \alpha_i f(n-i)]. \]

为什么这种方式能够更易编码, 比如, 常见的:

\[\hat{f}(n) = f(n-1), \]

则

\[e(n) = f(n) - f(n-1), \]

我们知道, 序列的前后往往具有相关性, 甚至是相同的, 这就会导致\(e(n)\)会出现大量重复的元素, 从而能够更好地编码. 当然, 我们需要额外编码\(f(0)\)作为起点.

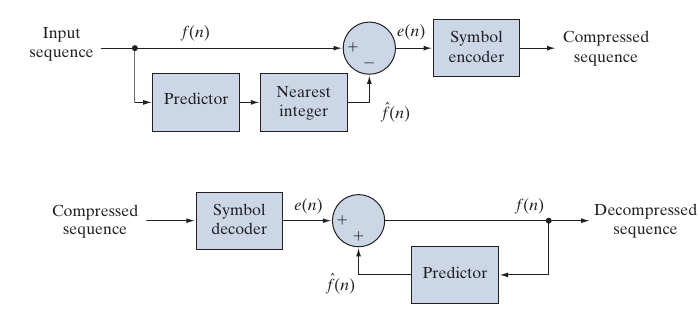
2D, 3D是类似地:

\[\hat{f}(x, y) = \mathrm{round} [\sum_{i=1}^m] \alpha_i f(x, y-i), \\ \hat{f}(x, y, t) = \mathrm{round} [\sum_{i=1}^m] \alpha_i f(x, y, t-i). \\ \]

还有一种有损的编码, 通过某种方式, 将\(e(n)\)映射为自由度更小的\(\dot{e}(n)\), 比如:

\[\dot{e}(n) = \left \{ \begin{array}{ll} +\xi & \text{for} \: e(n) > 0, \\ -\xi & \text{otherwise}. \end{array} \right . \]

在通过\(\dot{e}(n)\)解码的时候,

\[\hat{f}(n) = \alpha \dot{f}(n-1), \\ \dot{f}(n) = \dot{e}(n) + \hat{f}(n), \]

并输出\(\dot{f}(n)\).

下表就是一个例子, 其中\(\xi=6.5\).

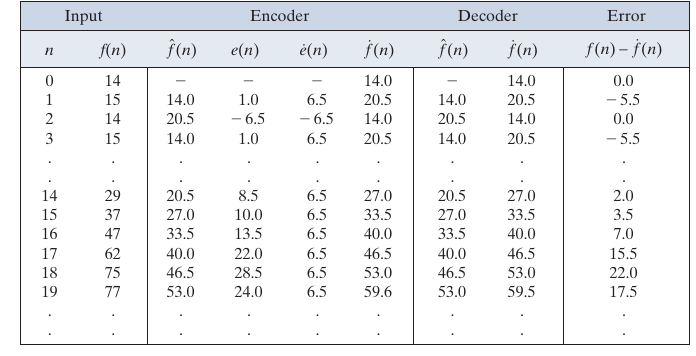
Optimal Predictors

即:

\[\min_{\alpha} E[f(n) - \hat{f}(n)]^2 \\ \mathrm{s.t.} \quad \hat{f}(n) = \sum_{i=1}^m \alpha_i f(n-i). \]

最优解为:

\[\alpha = R^{-1}r, \\ R_{i, j} = E[f(n-i)f(n-j)], \\ r_{k} = E[f(n)f(n-k)]. \\ \]

Optimal Quantization

\[\min_{s, t} \sum_{i=1}^{(\frac{L}-1)/2}\int_{s_{i-1}}^{i} (s - t_i) p(s) \mathrm{d}s. \]

KKT条件为:

\[\int_{s_{i-1}}^{s_i}a(s-t_i)p(s) \mathrm{d}s = 0, \quad i=1, 2, \cdots, \frac{L}{2}, \\ s_i = \left \{ \begin{array}{ll} 0 & i=0, \\ \frac{t_i + t_{i+1}}{2} & i=1, 2, \cdots, \frac{L}{2} - 1, \\ \infty & i = \frac{L}{2}. \end{array} \right . \]

具体的解见Lloyd-Max quantizers (p613).

Wavelet Coding

JPEG-2000.

即对每个Block采取小波变换, 如下图所示, 通常除了左上角, 其余元素值很低, 通过设定阈值, 可以导致稀疏化.

posted @ 2021-08-18 17:23  馒头and花卷  阅读(239)  评论(0)  编辑  收藏  举报