概率与期望
继数论和组合之后的第3大数学巨坑
基本概念和符号表述
该部分可参考必修二(人教版)最后一章,本质上是使用集合描述概率
-
随机事件:满足下列条件的现象
- 可以在相同的条件下重复进行
- 实验结果不止一个,且所有结果可以事先预知
- 实验前不确定出现什么结果
-
样本空间 \(\Omega\): 随机试验所有可能结果组成的集合
-
样本点:\(\Omega\)中的元素,即一个结果就是一个样本点
-
随机事件(集合下):\(\Omega\)的子集
-
\(A\)事件发生:\(A\)事件包含的样本点中有一个样本点出现(成为实验后的结果)
-
事件类型:在某条件下根据发生情况分类,具体包括:
- 基本事件:由一个样本点组成的单个元素的集合
- 必然事件:在某条件下必然发生,叫做相对于该条件的必然事件
- 不可能事件:在某条件下不可能发生,叫做相对于该条件的不可能事件
- 随机事件:在某条件下可能发生,也可能不发生,叫做相对于该条件的随机事件
-
频数和频率:在相同条件下重复\(n\)次实验,事件\(A\)发生的次数\(n_A\)叫做事件\(A\)的频数 \(f = \frac{n_A}{n}\)叫做事件\(A\)出现的频率
-
概率:事件\(A\)的频率的稳定值(看似随意,实则是大数定律)
-
事件的关系与运算:运用集合运算进行事件转化和概率计算
关系 定义 描述 包含 如果事件\(A\)发生,那么事件\(B\)一定发生 \(A \subseteq B\) 相等 \(B \subseteq A,A\subseteq B\) \(A = B\) 和(并)事件 \(A\)和\(B\)的和事件发生,当且仅当事件\(A\)发生或者事件\(B\)发生 \(A \bigcup B(A + B)\) 积(交)事件(同时发生) \(A\)和\(B\)的积事件发生,当且仅当\(A\)发生且\(B\)发生 \(A \bigcap B(AB)\) 互斥事件 \(A \bigcap B\)为不可能事件 \(A \bigcap B = \emptyset\) 对立事件 不是发生\(A\),就是发生\(B\) \(A \bigcap B = \emptyset,A \bigcup B = \Omega\),此时\(P(A \bigcup B) = P(A) + P(B) = 1\) -
古典概型:实验结果可推知,无需任何统计试验,通常满足:
- 样本空间有限
- 每个结果出现的可能性相同
- 每个现象发生的事件互不相容
-
概率性质
- \(P(A \cup B) = P(A)+P(B) - P(A\cap B)\)
- \(A \cap B = \emptyset \to P(A\cup B) = P(A) + P(B)\)
- 若\(A_1 \sim A_n\)均互斥,那么
\[P(\bigcup\limits_{i = 1}^nA_i) = \sum\limits_{i = 1}^nP(A_i) \]- 有\(n\)个独立事件(自己是否发生不影响其他事件是否发生),那么
\[P(\bigcap\limits_{i = 1}^nA_i) = \prod\limits_{i = 1}^nP(A_i) \]
下列知识参考选修部分
-
条件概率 \(P(B|A)\):表示在\(A\)已经发生的条件下,\(B\)发生的概率,本质上是把\(B\)的样本空间换成了\(A\)集合
\[P(B|A) = \frac{n(AB)}{n(A)} = \frac{P(AB)}{P(A)} \]该种概率下有一些推论
- 若\(A,B\)互为独立事件,那么\(P(B|A) = P(B)\)
- \(P(AB) = P(B|A)P(A)\)
- \(P(\Omega|A) = 1\)
- 若\(B\cap C = \emptyset\),那么\(P(B\cup C|A) = P(B|A)+P(C|A)\)
- \(P(\complement_\Omega B|A) = 1 - P(B|A)\)
-
全概率公式
设\(A_1\sim A_n\)两两互斥,\(\bigcup\limits_{i = 1}^nA_i = \Omega\),且\(P(A_i) > 0\),那么对\(\forall B \subseteq \Omega\),有\[P(B) = \sum\limits_{i = 1}^nP(A_i)P(B|A_i) \]简单理解:事件\(B\)有多种发生因素,那么事件\(B\)发生的概率等于每个因素导致\(B\)发生的概率之和
-
贝叶斯公式
设\(A_1\sim A_n\)两两互斥,\(\bigcup\limits_{i = 1}^nA_i = \Omega\),且\(P(A_i) > 0\),那么对\(\forall B \subseteq \Omega\),\(P(B)>0\),有\[P(A_i|B) = \frac{P(A_i)P(B|A_i)}{P(B)}=\frac{P(A_i)P(B|A_i)}{\sum\limits_{k = 1}^{n}[P(A_k)P(B|A_k)]}(分子也可写成P(A_iB)) \]简单理解:事件\(B\)有多种发生因素,现在事件\(B\)已经发生,那么该式子可求得\(B\)发生的原因是某一个因素的概率
-
期望 \(E(x)\) :事件\(A\)有多种结果,记其结果为\(x\),那么\(x\)的期望值表示事件\(A\)结果的平均大小
竞赛中,大多数是求一个离散型随机变量\(X\)的期望,如果\(X\)的输出值为\(x_i\),对应概率为\(P_i\),那么
\[E(X) = \sum\limits P_ix_i \]性质:
- \(E(x + c) = E(x) + c\)
- \(E(cx) = cE(x)\)
- 线性性质:记两个事件的结果为\(x,y\),那么\(E(x + y) = E(x) + E(y)\) ,\(E(xy) = E(x)E(y)\)(这个式子成立要求\(x,y\)相互独立)
应用
概率与期望常常和其他算法一起使用 (比如dp)
概率的一般套路就是
期望的一般套路就是根据定义:
注意这里的\(val\)可能是\(dp\)数组
Bag of mice
上来就\(dp\)
定义\(dp_{i,j}\)表示袋子里有\(i\)只白鼠,\(j\)只黑鼠时公主赢的概率
分类讨论转移
- 公主抓到白鼠,公主直接赢
- 公主抓到黑鼠,该龙了
但龙不能赢,所以龙抓到黑鼠
这两个事件相互独立,所以同时发生的概率是\(P(AB)=\frac{j}{i + j}\times \frac{j - 1}{i + j - 1}\)
接下来会有老鼠跑掉- 跑出白鼠,也就相当于抓一只白鼠放生
\[P(ABC_1) = P(AB)P(C_1|AB) = \frac{j}{i + j}\times \frac{j - 1}{i + j - 1}\times \frac{i}{i + j - 2} \]那么该事件发生后此时公主赢的概率就是老鼠抓完和跑掉后剩余老鼠对应情况的赢的概率,所以\[dp_{i,j} += P(ABC_1)\times dp_{i - 1,j - 2} \]- 跑掉黑鼠,同理
\[dp_{i,j}+= P(ABC_2)\times dp_{i,j - 3} = \frac{j}{i + j}\times \frac{j - 1}{i + j - 1}\times \frac{j - 2}{i + j - 2} \]
初始化:全是白鼠时公主必赢,没白鼠是龙只要等抓完了就能赢
for(int i = 1;i <= w;i++) dp[i][0] = 1;
for(int i = 1;i <= b;i++) dp[0][i] = 0;
for(int i = 1;i <= w;i++)
{
for(int j = 1;j <= b;j++)
{
dp[i][j] += (double) i / (i + j);
if(j >= 3)//防止越界
dp[i][j] += (double)dp[i][j - 3] * j / (i + j) * (j - 1) / (i + j - 1) * (j - 2) / (i + j - 2);
if(i >= 1 && j >= 2)
dp[i][j] += (double) dp[i - 1][j - 2] * j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2) ;
}
}
printf("%.9lf",dp[w][b]);
Jon and Orbs
翻译又是依托答辩
意思就是有\(k\)种物品,问什么时候取遍每种物品的概率符合题意(有些天可能抽到同一种物品)
设\(dp_{i,j}\)表示过了\(i\)天,取了\(i\)件,取遍了\(j\)种的概率
要从前一天转来,考虑第\(i\)天取的东西的种类
- 取的物品种类先前已出现,\(P = \frac{j}{k}\)
- 取得东西种类先前未出现,那么前\(i - 1\)天只取遍了\(j - 1\)种,新种类有\(k - (j - 1)\)种,\(P = \frac{n - j + 1}{k}\)
初始化:\(dp_{0,0} = 1\)
\(dp\)完后按要求找答案即可
dp[0][0] = 1;
for(int i = 1;i <= 10005;i++)//也不知道是第几天,多弄点
{
for(int j = 1;j <= x;j++)
{
dp[i][j] += (double) j / x * dp[i - 1][j];
dp[i][j] += (double) (x - j + 1) / x * dp[i - 1][j - 1];
}
}
P1365 WJMZBMR打osu! / Easy
还是\(dp\),一道期望\(dp\)
考虑到啊期望的计算还和连续\(o\)的长度有关,所以需要再开一个数组记录长度(的期望)
设\(f_i\)表示到了第\(i\)位的总期望,\(g_i\)表示到了第\(i\)位的期望长度
对于长度为\(k\)的连击序列,如果下一位还是\(o\),那么该位的贡献就是\((k + 1)^2 - k^2 = 2k + 1\)
为了方便,我们规定在\(g\)中,每一位的贡献是\(1\)
如果第\(i\)位能和前面连起来,说明第\(i\)位是\(o\)的概率为\(1\),那就是
转移:
- \(s_i == x\),说明对于这一位,贡献为\(0\)的概率为\(1\),和前面的连击连起来,即\(g_{i-1}+1\)的概率是\(0\),那么\[g_i=E(i) = 0 \times 1 + 0 \times (g_{i - 1}+ 1) = 0 \]此时\[f_i = E(i) + E(i - 1) = 0 \times (2g_{i - 1} + 1) + f_{i - 1} = f_{i - 1} \]
- \(s_i = o\),类比上面的计算,发现贡献\(E(i)\)中乘的概率是\(1\),所以得到\[f_i = f_{i - 1} + 2g_{i - 1} + 1,g_i = g_{i - 1} + 1 \]
- \(s_i = ?\),乘的概率变为\(0.5\)
答案:\(f_n\)
for(int i = 1;i <= n;i++)
{
if(s[i] == 'x')
{
f[i] = f[i - 1];
g[i] = 0;
}
if(s[i] == 'o')
{
f[i] = f[i - 1] + 2 * g[i - 1] + 1;
g[i] = g[i - 1] + 1;
}
if(s[i] == '?')
{
f[i] = 0.5 * (2 * g[i - 1] + 1) + f[i - 1];
g[i] = 0.5 * (g[i - 1] + 1);
}
}
printf("%.4lf",f[n]);
来看看他的兄弟:
P1654 OSU!
这里的单点贡献变成了\((x+1)^3-x^2=3x^2+3x+1\),每次乘的概率变成了\(p_i\)
其中,\(3x^2\)这一部分可以利用上一道题的结论维护
int n;
double a[N];
double f[N],g[N],h[N];
// g:x^2 h:x
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%lf",&a[i]);
for(int i = 1;i <= n;i++)
{
double u = 3 * g[i - 1] + 3 * h[i - 1] + 1;//单点贡献
f[i] = a[i] * u + f[i - 1];
g[i] = a[i] * (g[i - 1] + 2 * h[i - 1] + 1);//上一题结论
h[i] = a[i] * (h[i - 1] + 1);//x的维护
}
printf("%.1lf",f[n]);
return 0;
}
那能不能不用上一题的结论呢
double u = 3 * h[i - 1] * h[i - 1] + 3 * h[i - 1] + 1;//单点贡献
f[i] = a[i] * u + f[i - 1];
h[i] = a[i] * (h[i - 1] + 1);//x的维护
很遗憾,这样是错的
简单理解就是:期望的转移只满足线性性质(类似一次函数),多次方的运算对期望来说是不成立的
或者说,期望相乘需要满足事件相互独立,能相互独立的肯定不是同一件事件,所以不支持幂运算
P4316 绿豆蛙的归宿
这道题拉开了期望\(dp\)的经典套路:倒推
\(dp_i\)表示\(i\)点的期望
这道题就是通过\(dfs\)把答案汇总到\(dp_1\),末节的\(dp_n\)就是\(0\)
转移:
意即每次累加走到\(v\)的贡献\(\times\) 对应概率,即除以\(i\)的出度数
但为什么样例都过不了还能\(A\)呀?!?!
不同之处就在于给点打不打\(vis\),我本人觉得这是没必要的操作,因为题目也没规定,要是纯按概率走也会出现重复经过点的情况
就挺奇妙
void dfs(int x)
{
if(x == n)
{
dp[n] = 0;
return;
}
//if(vis[x]) return;
//vis[x] = 1;
for(int i = head[x];i;i = e[i].next)
{
int k = e[i].to;
dfs(k);
dp[x] += (dp[k] + 1.0 * e[i].val) / out[x];
}
}
P1297 [国家集训队] 单选错位
规定每个选择做对的贡献都是\(1\)
题意即为第\(i\)道题的正确答案飞到了第\(i+1\)道题上求作对概率和(期望每次的累加就是\(\frac{1}{k}\),相当于概率和),此时第\(i+1\)题上的答案范围就是\([1,a_i]\)
那么,在这种情况下做对第\(i+1\)题当且仅当两道题答案一样
一样的结果有\(\min(a_i,a_{i+1})\)种,总结果有\(a_i\times a_{i+1}\)种,因此
坑点:还有\(a_1,a_n\)要比较
double ans = 0;
for(int i = 2;i <= n;i++) ans += (double)1.0 * 1 / (max(a[i],a[i - 1]));
ans += (double) 1 / (max(a[1],a[n]));//不能忘
printf("%lf",ans);
[bzoj1419]Red is good
设\(dp_{i,j}\)表示当前剩下\(i\)张红牌,\(j\)张黑牌时的期望
-
不翻,获得分数的概率为\(0\),\(dp_{i,j} = 0\)
-
翻,那么就是翻到红牌的期望和翻到黑牌的期望之和
此时翻到红,黑牌的概率\(P_r = \frac{i}{i + j},P_b = \frac{j}{i + j}\),贡献题目有说,是\(1/-1\)
此时\[dp_{i,j} = dp_{i-1,j}\times P_r + dp_{i,j - 1} \times P_b \]
上述两种情况取\(\max\)即可
卡空间的话滚动一下就好
初始化:\(dp_{i,0} = i\),因为这时咋抓都是得分,故此时的期望就是\(\sum\limits_{l = 1}^i(1 \times P_r(=1))=i\)
坑点:保留时不四舍五入,要利用整型“断尾”特点来搞
double init(double x)
{
int u = x * 1000000;
return u * 1.0 / 1000000;
}
for(int i = 1;i <= r;i++)
{
dp[i % 2][0] = 1;
for(int j = 1;j <= b;j++)
{
//dp[i][j] += dp[i - 1][j - 1];
dp[i % 2][j] = max((d)(dp[i % 2][j - 1] - 1.0) * j / (i + j) + (dp[(i - 1) % 2][j] + 1.0) * i / (i + j),0.0);
}
}
答案:dp[r][b]
或者还可以定义为拿了\(i,j\)张牌,这时就是倒推,但原理相同
for(int i = x;i >= 0;i--)
{
dp[i % 2][y + 1] = r - i;
for(int j = y;j >= 0;j--)
{
dp[i % 2][j] = max(0.0,(dp[(i + 1) % 2][j] + 1) * 1.0 * (r - i) / (r + b - i - j) + (dp[i % 2][j + 1] - 1) * 1.0 * (b - j) / (r + b - i - j));
}
}
答案:dp[0][0]
[bzoj2720][Violet 5]列队春游
为了方便,可以先对数据排序,方便获得有多少人比他高/矮
对于第\(i\)个人,我们尝试计算他的贡献及对应的概率
假设现在求第\(i\)个学生(枚举的是数值不是位置)的视野(自身和比他矮的,算上自身是为了乘贡献时方便)为\(k\),那么\(k \in [1,n]\)
再设身高不低于第\(i\)个学生的人数为\(H(i)\)
那么,达到贡献\(k\)有两种方法
-
第一个比他高的是老师
这时\(1\sim k - 1(不算自己)\)的人都比第\(i\)个人要矮,排列方案有\(A_{n - H_i - 1}^{k - 1}\),总数为\(A_{n}^k\)\[ans += k \times \frac{A_{n - H_i - 1}^{k - 1}}{A_{n}^k} \] -
第一个比他高的是同学
这时要求\(k \leqslant n - 1\),因为\(k=n\)时只能是老师比他高那么这就要满足
- \(i - k + 1\sim i - 1(区间长为k - 1,同样不计本人)\) 都比他矮
- \(i-k\)处的人身高不低于他
实现第一个限制的方案数为\(A_{n - H_i-1}^{k - 1}\),实现第二个方案的方案数是\(H_i\),这时涉及到的区间长度是\(i - (i-k)+1 = k + 1\),所以总情况是\(A_{n}^{k + 1}\)
又因为这个长度为\(k + 1\)的区间可以左右移动,每一个不同的位置都是一个上述情况,而\(n\)中一共有\(n - (k + 1) + 1 = n - k\)个这样的区间,所以还要乘一个\(n - k\)
\[ans += k \times (n - k) \times H_i\times \frac{A_{n - H_i-1}^{k - 1}}{A_{n}^{k + 1}},k \in [1,n - 1] \]枚举\(i,k\)统计答案即可
double ans = 0;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
ans += j * A[n - h[i] - 1][j - 1] / A[n][j];//老师贡献
if(j <= n - 1)
ans += (double)j * (n - j) * h[i] * A[n - h[i] - 1][j - 1] * 1.0 / A[n][j + 1];//学生贡献
}
}
//上面的码子会输出-nan,得用一种叫long double的东西
//由于本蒟蒻不知道对应的printf类型,还得用神秘setpresicion(2)
\(O(n^2)\) 开开科技卡精度防-nan能过
法二:\(O(n)\)法
好像是能把一个\(i\)的期望和变成所有可能的\(k\)对应的概率之和
意思就是
但我不会,想不到\(E(i)\)里面乘的权值是怎么省略的
\(\cdots\)
烦了,直接暴力一下
法一可写成
注意到前面的\(\sum\)中若\(j = n\),只有当\(H_i=0\)时结果为\(1\),其余均为\(0\),而\(H_i=0\)也只能有一个(最高且没有相同身高的人),单拎出来该情况,后续处理
所以接下来所有\(H_i\geqslant 1\),\(j=n\)时就是\(0\)
那么写成
化简(式中\(H_i\geqslant 1\))
接下来对于\(\sum\limits_{j = 1}^{n - 1} jC_{n-j}^{H_i}\)
考虑到\(j=n\)时\(H_i\geqslant 1,C_{0}^{H_i}=0\),所以
\(\sum\limits_{j = 1}^{n - 1} jC_{n-j}^{H_i} = \sum\limits_{j = 1}^{n} jC_{n-j}^{H_i}\)
这时想起
求\(T_n = \sum\limits_{i = 1}^n(if_i)\)
这时矩阵里的trick,这里可以类比使用
定义\(S_i = \sum\limits_{k = 1}^{i}C_{n - k}^{H_i}\)
那么原式子就是\(nS_n-\sum\limits_{i= 1}^{n - 1}S_i\)
现在化简\(S_i\)
考虑公式
上式末尾是一个\(C_{n - i}^{H_i}\),补一个\(+C_{n-i}^{H_i+1}-C_{n-i}^{H_i+1}\),合并得到
带入:
所以
一般情况化简完毕,考虑\(H_i = 0\)
首先期望的表达式要补\(1\)
其次,组合化简时\(nC_{0}^{0} = n\),所以
其他一致,带入
同样符合结论
至此总结,可以得到
\(O(n)\)算法得证
暴力算完之后又把直接推出的方法看了看
先前计算贡献为\(k\)时的期望,相当于限定了区间长\(L\)只能是\(k\),并且这\(k\)个人紧挨着\(i\)
而实际上连续的\(k\)个人也能在\(L\geqslant k\)时产生贡献,此时他们不一定连着\(i\),可能只是长为\(L\)的视野中的一部分,那么这样就相当于把原来要乘的贡献拆成了一个一个小段,每个小段的权值都是\(1\),那么就变成了
这里,由于\(k\)个人不一定连着\(i\),概率的计算方式要改变
不变的是 这\(k\)个人和\(i\)的相对关系
考虑到沿用先前的定义,这里把\(k\)重定义为\(k\)个比\(i\)高的人,那么\(k\)就是\(H_i\)
这\(k\)个人和\(i\)自由排列方案是\(A_{n}^{k+1}\)
考虑到相对关系不变,即那\(k\)个人只能在\(i\)后面,即\(n-i\)个位置,方案\(A_{n-i}^{k}\)
又因为 \(i\)不一定连着\(k\),所以放置位置为\([0,n-i]\)(把老师也算进去),有\(n-i+1\)种选择
所以
化简从略,肯定比上面简单些,但结果是一样的
[bzoj2969]矩形粉刷
首先每次选的矩形的尺寸不好把握,再结合期望的线性,可以计算单个方格的期望,又因为一个方格的贡献就是\(1\)(面积为一,且只会产生一次贡献,即被刷上之后不再产生贡献),所以就是概率和
但正是因为一个格子只会被上一次色,我们难以得知这一次是\(k\)次中的哪一次,所以不妨求得该格子\(k\)次都不会被刷到的概率,拿\(1\)减一下就好了
设格子坐标为\((x,y)\)
那么就要保证该点不在选择的两点确定的矩形中,因此选的两点在该点的同侧(上,下,左,右)
看图
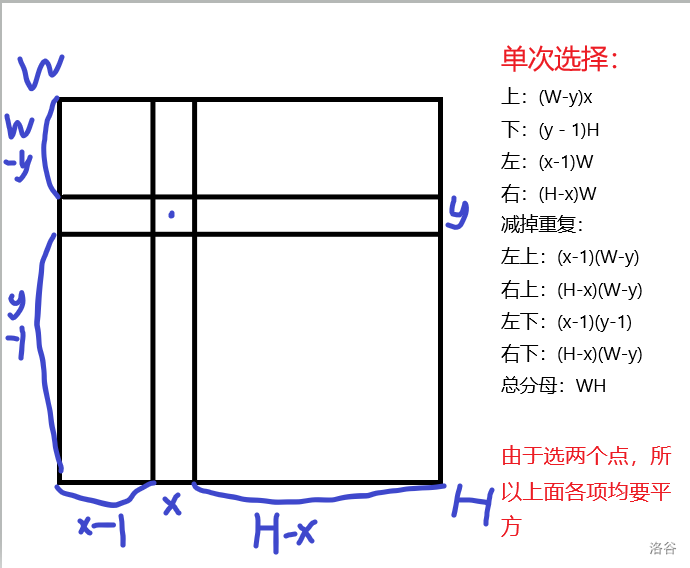
设算出的概率为\(P\),那么
又因为连续选\(k\)次,上面算的还是未刷上,所以一个点的贡献是\(1-P^k\)
求和即可,\(\sum(1-P^k)\)
坑点包括:
- 把\(double\)写成\(int\)
- 不考虑平方偷懒合并上面的项(比如前四项并成\((W-1)H+(H-1)W\))
- 算成\(\sum(1-P)^k,(1-\sum P)^k\),\(1-\sum P^k\)等
double init(double x)//这里也是double哦
{
return x * x;
}
int main()
{
int k,w,h;
scanf("%d%d%d",&k,&w,&h);
double ans = 0;
for(int i = 1;i <= w;i++)
{
for(int j = 1;j <= h;j++)
{
int x = j,y = i;
double kk = ((init((w - y) * h) + init((y - 1) * h) + init((x - 1) * w) + init((h - x) * w) - init((x - 1) * (w - y)) - init((h - x) * (w - y)) - init((x - 1) * (y - 1)) - init((h - x) * (y - 1))) * 1.0 / init((w * h)));//图中算法
//cout << kk << endl;
ans += 1 - pow(kk,k);
}
}
printf("%.0lf",ans);
return 0;
}
守卫者的挑战
应该是\(dp\),按照囊括要素\(N,L,k\)的方法定义
定义\(dp_{i,j,k}\)表示挑战了\(i\)场,成功了\(j\)次,当前背包容量为\(k\)
如果这一次失败了,继承上一次状态
如果成功了,那就是
这个方程对\(a_i=-1\)也同样适用
看到第三维会有一个问题:负数是否成立
回到题目
只需要完成所有\(N\)项挑战后背包容量足够容纳地图残片即可
也就是说,只要求终末状态的背包容量不为负数,中间转移时装不下了不要紧,可以等新背包出现
那么就要防止越界,启动学校食堂 (不是饿了是那道状压题)
有一个小问题:\(k \leqslant 2000,a_i\leqslant 1000\),好像开不下
但事实上最多得到\(n\)块碎片,也就是说有用的空间最多只有\(n\),防越界的话都加上一个\(n\)即可
那么,原先的负数域对应的就是\([0,n - 1]\),非负数对应的就是\([n,2n]\)
考虑到\(dp\)式中有\(l-a_i\),但\(a_i\)可能过大不好操控,因此把\(dp\)式写成\(i\to i +1\)的形式,,转移时求\(\min\)舍掉冗余空间即可
答案就是\(\sum dp_{n,l\sim n,n \sim 2n}\)
初始化:\(dp_{0,0,k+n} = 1\)
坑点:写成\(i\to i + 1\)形式后答案第一维会变成\(n+1\)
卡空间的话滚动即可
k = min(k,n);//舍掉冗余
dp[0][0][n + k] = 1;
for(int i = 0;i <= n;i++)
{
for(int j = 0;j <= n;j++)
{
for(int l = 0;l <= n * 2;l++)
dp[(i + 1) % 2][j][l] = dp[i % 2][j][l] * 1.0 * (1 - p[i]);
}
for(int j = 0;j <= n;j++)
{
for(int l = 1;l <= n * 2;l++)
{
int kk = min(l + a[i],2 * n);//舍掉冗余
dp[(i + 1) % 2][j + 1][kk] += dp[i % 2][j][l] * 1.0 * p[i];
}
}
}
double ans = 0;
for(int i = l;i <= n;i++)
{
for(int j = 0;j <= n;j++)
{
ans += dp[(n + 1) % 2][i][j + n];//第一维变成n + 1
}
}
printf("%.6lf",ans);
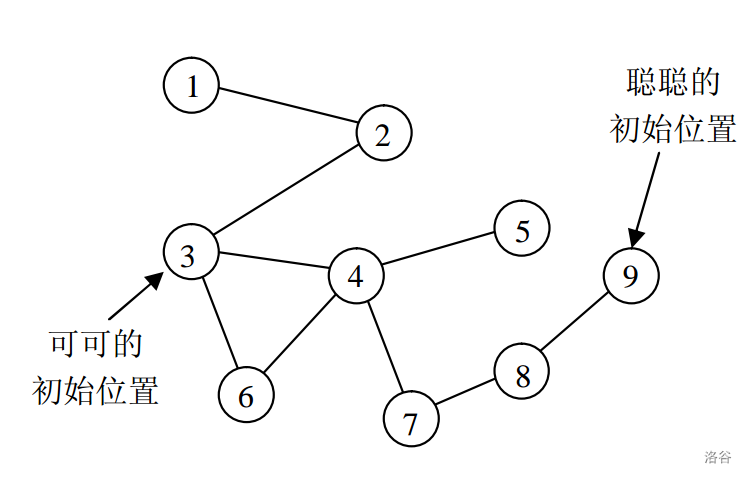
P4206 [NOI2005] 聪聪与可可
题目的关键是这两步其实算一个时刻,而题目更确切的是在求时刻的期望
对于样例
解析:
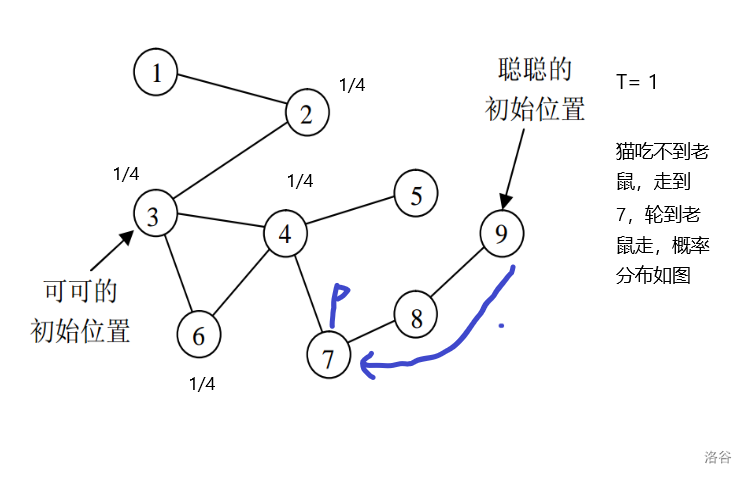
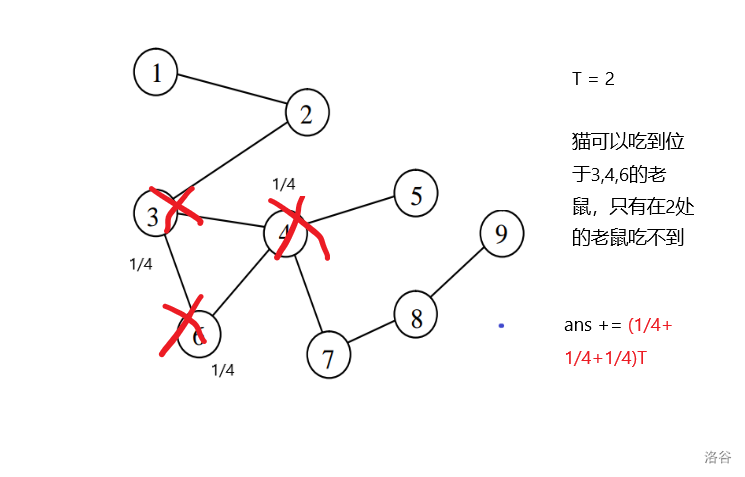
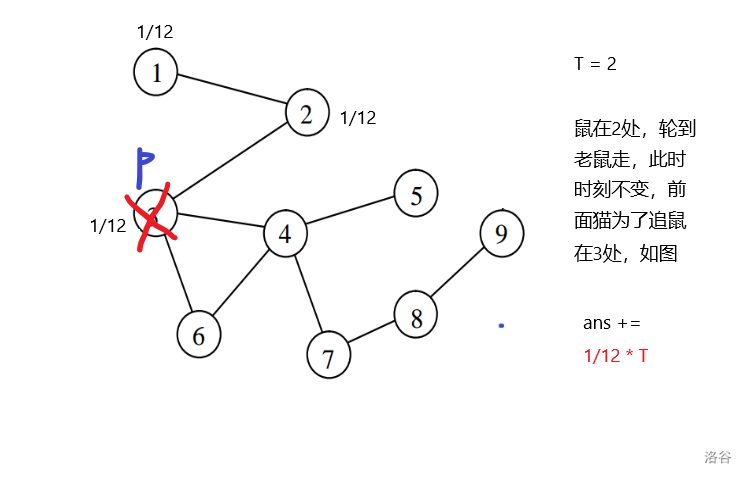
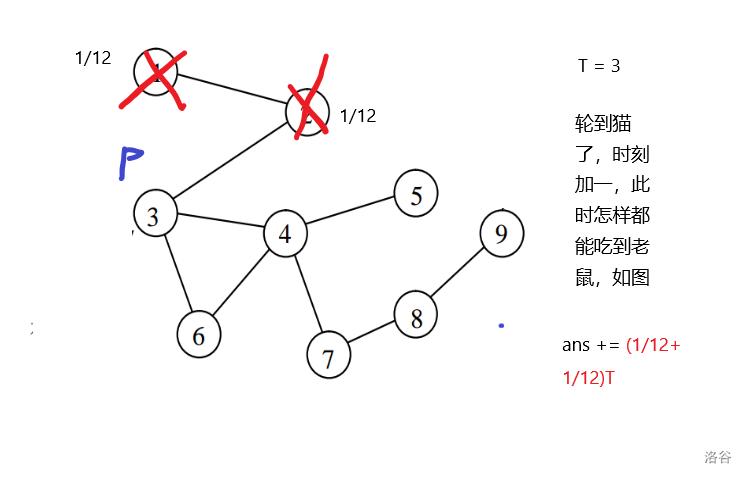
结果就是\(\frac{3}{4}\times 2 + \frac{1}{12}\times 2 + \frac{2}{12} \times 3 = 2 + \frac{1}{6} = 2.167\)
首先猫所谓的“离老鼠最近的景点”应该涉及到最短路,可以预处理
void init()
{
for(int i = 1;i <= n;i++)for(int j = 1;j <= n;j++) d[i][j] = 2005;
for(int i = 1;i <= n;i++)
{
dijkstra(i);
for(int j = 1;j <= n;j++) dt[i][j] = dt[j][i] = dis[j].w;
dt[i][i] = 0;
}//处理出任意两点间的最短路
for(int i = 1;i <= n;i++)
{//枚举老鼠
for(int j = 1;j <= n;j++)//枚举猫
{
for(int u = 0;u < e[j].size();u++)//枚举猫可能的下一步
{
int v = e[j][u];
if(dt[v][i] == dt[j][i] + 1)//如果枚举的落脚点在i,j间的最短路上
{
d[v][i] = min(d[v][i],j);//还要注意标号最小
}
}
}
}
}
定义\(d_{i,j}\)表示当前猫在\(i\)点,老鼠在\(j\)点时猫的选择
那么如果同一时刻内猫要走两步,下一步就是\(d_{d_{i,j},j}\)
定义\(dp_{i,j}\)表示猫在\(i\),老鼠在\(j\)处时的期望步数
那么,猫鼠在同一个点时\(dp_{i,j} = 0\)
答案的累加考虑使用\(dfs\)的回溯实现
规定猫走一个时刻的权值为\(1\)
分类讨论:
-
猫能在自己的回合内吃到老鼠
即\(d_{i,j} = j\)或\(d_{d_{i,j},j} = j\),那么\(dp_{i,j} = 1\)(百分之百抓到老鼠)
-
猫不能吃到
设\(d_{d_{i,j},j} = k,k \neq j\)
那么此时轮到老鼠走了,设老鼠:\(j \to l\),那么新情况就是\(dp_{k,l}\),概率是\(\frac{1}{out_j}\),可以使用\(dfs\)累加,即
\[dp_{i,j} = \sum\limits_{j \to l}(dp_{k,l}\times \frac{1}{out_j}) \]注意这里\(l\)还能是\(j\)
写出代码
double dfs(int mao,int shu)
{
if(mao == shu) return (dp[mao][shu] = 0);
int s1 = d[mao][shu];
int s2 = d[s1][shu];
if(s1 == shu) return (dp[s1][shu] = 1);
if(s2 == shu) return (dp[s2][shu] = 1);
for(int i = 0;i < e[shu].size();i++)
{
int k = e[shu][i];
dp[mao][shu] += dfs(s2,k) * 1.0 / (out[shu] + 1);
}
dp[mao][shu] += dfs(s2,shu) / (out[shu] + 1);
return dp[mao][shu];
}
发现又\(WA\)又\(TLE\)
\(WA\)是因为没谈到初始化状物
对于初始化,\(dfs\)中的两个连续的\(if\)就是在模拟猫走的过程,那么\(if\)完了之后猫就走过了,此时权值要加\(1\),
对于\(TLE\),可以使用记忆化思想,给走过的点打\(vis\),如果访问过了直接\(return\)即可
double dfs(int mao,int shu)
{
if(ifvis[mao][shu]) return dp[mao][shu];//走过了直接return省时间
if(mao == shu) return (dp[mao][shu] = 0);
int s1 = d[mao][shu];
int s2 = d[s1][shu];
if(s1 == shu) return (dp[s1][shu] = 1);
if(s2 == shu) return (dp[s2][shu] = 1);//模拟猫的走法
dp[mao][shu] += 1;//猫走完了
for(int i = 0;i < e[shu].size();i++)
{
int k = e[shu][i];
dp[mao][shu] += dfs(s2,k) * 1.0 / (out[shu] + 1);
}//累加老鼠的走法
dp[mao][shu] += dfs(s2,shu) / (out[shu] + 1);//别忘了还可能留在原地
ifvis[mao][shu] = 1;//打标记
return dp[mao][shu];//返回答案
}
P2059 [JLOI2013] 卡牌游戏
只有一个人的时候最简单,百分之百赢
如果有两个人,那获胜概率就是奇数/偶数的占比,这取决于谁坐庄。
如果有三个人,可以通过让一个人毙业进入只有两个人的状态,这启示我们可以尝试使用\(dp\)
先设\(dp_{i}\)表示当前剩了\(i\)个人,方向是\(i-1\to i\)
考虑到题目要求所有人的胜率,所以还得加一维枚举人头
再定义\(dp_{i,j}\)表示场上有\(i\)个人,第\(j\)个人的胜率
这里要注意的是由于人毙业后其他人的相对位置会改变,所以这里的第\(j\)个表示从新庄家开始数第\(j\)个人,为了方便,后面的第..个均是从庄家开始数
假如抽到了\(a\),那么毙业的就是第\(a \%i\)个人,设为\(k\)
那么此时\(k+1\)变为庄家,则对于原先第\(j\)个人,如果\(k < j\),那么他的新位置就是\(j - (k + 1) + 1 = j - k\) ,否则就是\(i -k+j\)。这样做是为了保证一个人的胜率转移是连续的
一共有\(m\)种抽牌情况,那么每次毙业的概率就是\(\frac{1}{m}\),所以得到
最后每个人的胜率就是\(dp_{n,i}\)
初始化:最前面提到的百分百获胜:\(dp_{1,1} = 1\)
dp[1][1] = 1;
for(int i = 2;i <= n;i++)
{
for(int j = 1;j <= i;j++)
{
for(int l = 1;l <= m;l++)
{
int k = a[l] % i;
if(k < j) dp[i][j] += dp[i - 1][j - k] * 1.0 / m;
if(k > j) dp[i][j] += dp[i - 1][i - k + j] * 1.0 / m;
}
}
}
P1850 [NOIP2016 提高组] 换教室
最短路什么的预处理就好了的说
for(int k = 1;k <= v;k++)
for(int i = 1;i <= v;i++)
for(int j = 1;j <= v;j++)
dis[i][j] = min(dis[i][j],dis[i][k] + dis[k][j]);//floyd的矩阵存图方便后期dp式的表示
囊括要素定义\(dp\):设\(dp_{i,j,1/0}\)表示当前在时刻\(i\),申请了\(j\)次,第\(i\)个时段有/没有申请(因为题目说了甚至可以一次也不申请)时的期望
根据期望定义,\(新期望 = 旧期望+权值 \times 概率\)
大力分类讨论
- 没申请第\(i\)课时
- 没申请第\(i-1\)课时,那么前后两次百分之百是在原来的教室,即\(c_i,c_{i-1}\)\[dp_{i,j,0} = dp_{i-1,j,0} + dis(c_i,c_{i-1}) \]
- 申请了第\(i-1\)课时,但是不一定能申请成功,要乘概率的,申请成功的概率为\(p_{i-1}\),不成功的话拿\(1\)减一下就好了\[dp_{i,j,0} = dp_{i-1,j,1} + p_{i-1} \times dis(c_i,d_{i-1}) + (1-p_{i-1})dis(c_i,c_{i-1}) \]
- 没申请第\(i-1\)课时,那么前后两次百分之百是在原来的教室,即\(c_i,c_{i-1}\)
上述情况比个\(\min\)
- 申请了第\(i\)课时
- 没申请第\(i-1\)课时,那么只可能是\(c_i\to d_i\)\[dp_{i,j,1} = dp_{i-1,j -1,0} + p_i \times dis(d_i,c_{i-1}) + (1 - p_i)dis(c_i,c_{i-1}) \]
- 申请了第\(i - 1\)课时,共计四种情况
- 均成功\[val_1 = p_i \times p_{i-1}\times dis(d_i,d_{i-1}) \]
- 只成功一个,要么前成后不成,要么前不成后成\[val_2 = (1 - p_i)p_{i-1} \times dis(c_i,d_{i-1}) \]\[val_3 = p_i(1 - p_{i-1})dis(d_i,c_{i-1}) \]
- 均不成功\[val_4 = (1 - p_i)(1 - p_{i-1})dis(c_i,c_{i-1}) \]
\[dp_{i,j,1} = dp_{i-1,j-1,1} + val_1 + val_2 + val_3 + val_4 \] - 均成功
- 没申请第\(i-1\)课时,那么只可能是\(c_i\to d_i\)
上述情况取\(\min\)
初始化:\(dp_{i,0,0} = dp_{i-1,0,0} + dis(c_i,c_{i-1})\),就是申请前的最短路
坑点:
- \(dp_{i,0,1}\)并不存在,这种情况就没必要(也不能)做第二大情况的转移(不写的话\(44pts\))
- 可能一次也不申请才是最优解(不写的话\(76pts\))
- 不能用memset(写了的话\(20pts\))
for(int i = 1;i <= n;i++) for(int j = 1;j <= m;j++) dp[i][j][0] = dp[i][j][1] = inf;// No memseting
for(int i = 1;i <= n;i++) dp[i][0][0] = dp[i - 1][0][0] + dis[c[i]][c[i - 1]];//初始化
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= i;j++)
{
int c1 = c[i],c2 = c[i - 1],d1 = d[i],d2 = d[i - 1];
dp[i][j][0] = min(dp[i][j][0],dp[i - 1][j][0] + dis[c1][c2]);
dp[i][j][0] = min(dp[i][j][0],dp[i - 1][j][1] + 1.0 * p[i - 1] * dis[c1][d2] + 1.0 * (1 - p[i - 1]) * dis[c1][c2]);
dp[i][j][1] = min(dp[i][j][1],dp[i - 1][j - 1][0] + 1.0 * p[i] * dis[d1][c2] + 1.0 * (1 - p[i]) * dis[c1][c2]);
if(j == 1) continue;//卡掉没必要申请的情况
double num1 = 1.0 * p[i] * p[i - 1] * dis[d1][d2];
double num2 = 1.0 * p[i] * (1 - p[i - 1]) * dis[d1][c2];
double num3 = 1.0 * (1 - p[i]) * p[i - 1] * dis[c1][d2];
double num4 = 1.0 * (1 - p[i]) * (1 - p[i - 1]) * dis[c1][c2];
dp[i][j][1] = min(dp[i][j][1],dp[i - 1][j - 1][1] + num1 + num2 + num3 + num4);
}
}
double ans = inf;
ans = min(ans,dp[n][0][0]);//没申请
for(int i = 1;i <= m;i++)
{
ans = min(ans,min(dp[n][i][0],dp[n][i][1]));
}
printf("%.2lf",ans);
P2473 [SCOI2008] 奖励关
\(n \leqslant 15\),状压(CaO)
套路的先写出\(dp_{i,S,1/0}\),表示当前是第\(i\)次吃宝物,此时吃的宝物种类状态是\(S\)(每一位表示吃没吃过),这一次吃还是不吃
处理每个宝物的前置状态不消说
然后发现要吃的话如果不满足前置状态也吃不了,相当于没吃,好像第三维没什么卵用,也就是说吃还是不吃只在能吃的情况下抉择,不是统一情况,这种东西放到比\(\max\)里实现
如果第\(i\)次吃了宝物\(j\),那么
这里启示我们可以使用倒序,即
如果放弃吃,那么两次状态一样
如果要吃,那就选择吃不吃
枚举\(i,S_i,j\),复杂度\(O(k2^nn)\)在承受范围内
写出代码:
for(int i = k;i >= 0;i--)
{
for(int s = 0;s <= (1 << n) - 1;s++)
{
if(check(s) > i) continue;//保证吃到的种类数不超过抽奖次数
for(int j = 1;j <= n;j++)
{
int news = 1 << (j - 1);
if(check(s | news) > i + 1) continue;
if((s & a[j]) != a[j]) dp[i][s] += dp[i + 1][s];
else dp[i][s] += max(dp[i + 1][s],dp[i + 1][s | news] + 1.0 * P * val[j]);//上面的式子
}
}
}
printf("%.6lf",dp[0][0]);
发现错得离谱
想了想发现道理也不复杂:抽到物品\(j\)的概率是\(P\),也就是说继承对应的期望的概率也是\(P\),这表明\(dp\)数组也得乘以概率,和上面题目中\(dfs\)的累加十分相似
for(int i = k - 1;i >= 0;i--)//细节:0~ k是k + 1次,要实现k次是0~k-1
{
for(int s = 0;s <= (1 << n) - 1;s++)
{
for(int j = 1;j <= n;j++)
{
int news = 1 << (j - 1);
if((s & a[j]) != a[j]) dp[i][s] += dp[i + 1][s] * P;
else dp[i][s] += max(dp[i + 1][s] * P,dp[i + 1][s | news] * P + 1.0 * P * val[j]);//全部乘以概率
}
}
}
//这里原先的check会带小常数增加TLE风险,其实卡掉的那一部分不影响dp,所以可以删掉
答案就是\(dp_{0,0}\),无需初始化
那么想一想,什么时候\(dp\)数组也要乘以概率?期望应该是只有新增的权值才乘以概率的呀?
很简单:条件概率模型
也就是说,只有当获得新权值的情况成为继承期望的“前提”时才要给期望乘以概率,此时继承期望就是“在该条件下发生的事件”
这样一来前面的都说的通了
\(dfs\)式期望很显然前一步是后一步的前提,比如猫抓老鼠中累加某点期望的前提就是老鼠走到那个点,所以一般都要乘以概率
而换教室之类就不一样,当前一步换不换教室和继承上一步的期望没有任何关联,是独立的,此时期望不乘以\(P\)
P4284 [SHOI2014] 概率充电器
(煞笔吧充电还看脸)
树形的,新品种
规定一个元件充上电的权值为\(1\),那么期望就是每个节点充上电的概率的和
设\(dp_i\)表示\(i\)点亮的概率
一个点充上电有三种可能:
- 自己充
- 被父亲充
- 被儿子充
第一条的实现就是初始化
后面两条如果同时考虑会很混乱(父亲充儿子不充,儿子充父亲不充,俩一块儿充,俩都不充...,而且这中间还可能相互重叠),所以考虑\(dfs\)两遍
由于一个点只能有一个父亲,但可能有一堆儿子,而且儿子之间相互独立。所以我们考虑先把儿子充的概率累计后在计算父亲充的概率
使用公式
对于节点\(x\)和他的一个儿子\(son\),由公式可得
就是
现在的\(dp\)数组存的是在\(x\)及其所有儿子的共同努力下\(x\)亮的概率(注意,是所有),也就是式中的\(P_x\),不妨记为\(dp^1_i\)
考虑父亲,把更新后的数组(答案)记为\(dp^2\)
还是利用公式:
这里有个小细节:如果要靠父亲充\(x\),那么父亲亮就不能靠\(x\),只能靠自己和其他儿子,把刨掉\(x\)后的\(dp_{fa}\)记作\(dp^x\)
即
接下来要想办法求解\(dp^x\)
我们回到汇总儿子充的计算式中,当\(x\)是\(fa\)的儿子时,套用上式并结合\(dp\)数组含义可得:
可以解得
回带入答案式\(dfs\)即可
坑点见代码
void dfs(int x,int fa)//汇总儿子的答案
{
for(int i = head[x];i;i = e[i].next)
{
int k = e[i].to;
if(k == fa) continue;
db num = e[i].w;
dfs(k,x);
dp[x] = (dp[x] + dp[k] * num - dp[x] * dp[k] * num);
}
}
void getans(int x,int fa)//此时存的都是dp1
{
for(int i = head[x];i;i = e[i].next)
{
int k = e[i].to;
db num = e[i].w;
if(k == fa) continue;
if(fabs(1 - dp[k] * num) > 1e-7)//坑1:不能除以0(极小值)
{
db dp_x = (dp[x] - dp[k] * num) * 1.0 / (1 - dp[k] * num);//求解dp_x
dp[k] = dp[k] + dp_x * num - dp[k] * dp_x * num;
}
getans(k,x);//坑2:别手滑写成dfs(doge)
}
}
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n - 1;i++)
{
int u,v;
db s;
scanf("%d%d%lf",&u,&v,&s);
add(u,v,s / 100.0);
add(v,u,s / 100.0);//坑3:记得化成小数
}
for(int i = 1;i <= n;i++)
{
int y;
scanf("%d",&y);
dp[i] = val[i] = 1.0 * y / 100.0;//初始化为点亮自己的概率
}
dfs(1,0);
getans(1,0);
db ans = 0;
for(int i = 1;i <= n;i++) ans += dp[i];
printf("%.6lf",ans);
return 0;
}
P3232 [HNOI2013] 游走
想到Piggies(巧了也是概率)
可以得到
对于计算\(P_e\),就是与之相连的点\(i\)花\(\frac{1}{out_i}\)的概率经过它,再考虑到可能经过多次,所以是点的期望经过次数和概率的乘积
接下来考虑计算点的经过次数(期望),结合联想到的题目和前面的概率题,可知使用\(n\)元一次方程组和\(Gaussian\) \(Elimination\)
设点\(i\)的期望经过次数为\(x_i\),仿照Piggies可知
考虑特殊点:
对于点\(1\),由于是起点,所以多一次经过
对于点\(n\),由于百分百到\(n\)并且不会由\(n\)走向其他点,所以上述方程中均不考虑\(n\)点
那么对于一条边,要么从左端点过来,要么从右端点过来
排序,让最小的概率乘最大的编号并累加即可
注:从概念上来说\(edgeP\)指的是一条边的期望经过次数,但是由于经过一次的贡献只有\(1\),所以数值上等于概率和
//前面有n--
a[1][n + 1] = -1;
for(int i = 1;i <= n;i++)
{
a[i][i] = -1;
if(vis[1][i]) a[1][i] = 1.0 / out[i];
}
for(int i = 2;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
if(i == j) continue;
if(vis[i][j]) a[i][j] = 1.0 / out[j];
}
}//弄系数矩阵
gauss();//Elimination
for(int i = 1;i <= m;i++)
{
int u = e[i].from;
int v = e[i].to;
e[i].Ex = a[u][n + 1] * 1.0 / out[u] + a[v][n + 1] * 1.0 / out[v];
}//求边的概率
sort(e + 1,e + m + 1,cmp);//从大到小排序
double ans = 0;
for(int i = 1;i <= m;i++) ans += i * e[i].Ex;//小编号*大概率
然而\(70pts\)
又看了看参考题目发现是\(eps\)精度不够,得开\(1e^{-10}\)及以下
6
P3211 [HNOI2011] XOR和路径
让我先捋捋重边和自环什么鬼
好像不影响
这应该是个异或方程组
发现这式子没法解,需要分离\(\oplus\)和\(+\)的操作
加减换成异或不太科学,考虑用加减模拟异或
那么这里就有了一个骚操作:把数拆成一位一位来搞,加减\(0/1\),因为位运算的各个位是互不影响的
那么改变\(x_i\)的含义:从\(i\)点出发走到\(n\)点,使得第\(i\)位为\(1\)的概率,对应的,\(edgeVal\in \{0,1\}\),此时他代表边权的第\(i\)位
还有一点就是
接下来考虑如何模拟
由于现在存的是位,那么除法不好实现,先乘过去
下面用\(val_s\)表示\(edgeVal(i,s)\)
结合位运算的性质,可得
但是为了使用高斯消元需要把这种式子写成方程的形式
当\(val_s = 0\)时,只有\(x_s=1\)才能贡献\(1\),那么累加的话可以直接累上去(反正\(+0\)没影响),那么当只有\(x_s=0\)时才贡献\(1\),就可以用\(1\)减一下
进一步变形就是
注:两个\(\sum\)是\(if-else\)的关系
那么如何汇总答案呢
根据\(x_i\)的定义,可知答案就都存在\(x_1\)里,那么
P3750 [六省联考 2017] 分手是祝愿
首先这种开关灯的题还是有些基本套路的
- 操作有周期性,每个灯操作一遍就行了
这道题的限制多了一个尿性:
- 操作\(i\)号灯时,只有编号\(\leqslant i\)的灯才会受到影响
这就表明:把右边大编号区间搞掉后就只用管左边小区间了
要实现这个,最直接的就是从右往左,遇到亮的就按一下,这样走到\(i\)时\(i\)后面的肯定都灭了
有了这个策略以后就可以得到部分分:\(k=n\)时哪怕就按照上述操作硬搞,最坏也是每个灯按一下,操作次数\(=n\leqslant k\)成立,不用随机 ,模拟就行 (竟然\(80pts\))
int main()
{
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
for(int i = n;i >= 1;i--)
{
if(a[i])//亮了按一下
{
ans++;
int u = i;
for(int j = 1;j <= sqrt(u) + 0.5;j++)//更新后面灯的状态
{
if(u % j == 0)
{
int h = u / j;
if(j != h) a[j] = !a[j],a[h] = !a[h];
else a[j] = !a[j];
}
}
}
}
for(int i = 1;i<= n;i++) ans = (ans * i) % mod;//按题目说的来
printf("%lld",ans);
return 0;
}
从上面的一点我们大胆猜测:操作次数\(\leqslant k\)(不再随机)的区间就是左边的\([1,k]\)(但里面的灯的状态可能不是初始态),而此时使用的操作次数最小的方案,就是上面用的那个
接下来考虑一般情况,那就要把随机的部分处理掉
这时就要思考随机操作对前后产生的影响
这时结合性质\(1\):随到亮的时是好方案,没随到就浪费了
从这一点想,可以得到如果不小心把灭的按亮了,肯定要花费一定的步数给他摁回去
那么,如果现在有\(i\)盏灯亮着,就会有\(\frac{i}{n}\)的概率按到亮的,变成\(i-1\)盏亮,有\(\frac{n-i}{n}\)的概率按到灭的,如果按到灭的,就变成\(i+1\)盏亮着,这时要先变回\(i\)盏灯亮的情况,再重复上述过程
这种重复可能无休止在前面遇到过,用的是高斯消元
设\(x_i\)表示当前亮了\(i\)盏,要按灭一盏到亮\(i-1\)时的期望步数,那么
发现每个方程的未知数不像上面图论那样乱重叠,呈现一定的线性。线性加上没乱重叠(无后效性),这个东西“退化”成了\(dp\)
化简
处理完了随机,还有一点:什么时候跳出随机?
考虑到\(dp\)没有使用区间相关物,如果按照上面的猜测,我们无法得知\(dp\)何时就进入了\([1,k]\)
那我们不妨再大胆一些:当场上就剩下\(k\)盏灯时就可以进行从右到左的扫荡,花费\(k\)次 (感觉很离谱对吧,但猜测就不管那么多了)
这样的话到\(dp_{k+1}\)就行了,最后加个\(k\)
这里会出现一个小细节:浮点数没法求余,所以边乘边求余不行了
这里可以使用逆元替换\(dp\)中的除法
接下来是\(dp\)对应细节:
- 全亮的时候肯定按到亮的,所以
- 结合\(dp\)数组含义,可知:\(dp_i\)表示的是\(i \to i - 1\)而不是全局答案,就像吃四个馒头吃饱了,让你饱的是四个馒头不是最后一个馒头,所以
最后还有一点:有可能初始态就是可进行最优解态,所以上面的代码留下,\(ans\)就是操作次数,如果\(ans \leqslant k\),就直接输出\(ans\)
v[1] = 1;
for(int i = 2;i <= n;i++) v[i] = (ll)(mod - mod / i) * v[mod % i] % mod;
for(int i = n;i >= 1;i--)
{
if(a[i])
{
sum++;
int u = i;
for(int j = 1;j <= sqrt(u) + 0.5;j++)
{
if(u % j == 0)
{
int h = u / j;
if(j != h) a[j] = !a[j],a[h] = !a[h];
else a[j] = !a[j];
}
}
}
}
dp[n] = 1;
for(int i = n - 1;i >= k;i--) dp[i] = (ll)(n + (n - i) * 1.0 * dp[i + 1]) * v[i] % mod;
if(sum <= k) ans = sum;
else
{
for(int i = k + 1;i <= n;i++) ans = (ans + dp[i]) % mod;
ans = (ans + k) % mod;
}
for(int i = 1;i <= n;i++) ans = (ans * i) % mod;
printf("%lld",(ans % mod + mod) % mod);
然鹅还是\(80pts\)
其中的原因在于 吃的馒头数量不对 累计\(dp_i\)的范围不对,我们不需要从\(n\)个灯亮的情况开搞,事实上,\(ans\)所代表的暴力法应当是理论上的最多操作次数,所以上限就是\(ans\)
for(int i = k + 1;i <= ans;i++) ans = (ans + dp[i]) % mod;
ps:关于从右往左扫,做题时还只是一个猜想,详细的论证见证明
「SDOI2017」硬币游戏
惯性思维干碎一地
看范围知高斯消元
或者认为可能会出现所有人一直都赢不了的无穷态,需要用到高斯消元
设第\(i\)个同学赢的概率是\(x_i\)
先从两个同学的情况入手
设人为\(A,B\),对应串为\(S_A,S_B\),游戏未结束时摇出来的是\(S\),长度为\(len_S,len_B,len_A\),摇出\(S_A,S_B,S\)的概率为\(P_A,P_B,P_S\)
比如\(S_A = THT\),\(S_B = TTH\)
很显然,游戏必然结束时就是\(S \to SS_A/SS_B\),但中间可能会提前结束
换句话说,我们不妨计算一下 \(S\to SS_A/SS_B\)的概率和\(A,B\)获胜的概率的关系(不考虑中断)
事实上,再换句话说:\(A,B\)的胜率其实是字符串达到某一特定状态的概率
也就是说,我们获得了两种角度来描述字符串的变化:一种是纯摇出来,一种是不断达到\(A,B\)要求的特定态,而由于描述的是同一变化,所以可以列含\(P_A,P_B\)的若干方程,从而解得\(P_A,P_B\)
不妨先说\(S\to SS_A\),从纯摇的角度来看达到这一状态的概率是\(P_S \times \frac{1}{len_A}\),例子中就是\(P_S\times \frac{1}{2^3}\),\(SS_A = STHT\)
接下来从\(A,B\)的特殊态角度看:
-
\(S\)以\(TH\)结尾,那么加上个\(T\)就结束了,概率是\(P_A\),根据上面说法 就是\(S \to ST\)的概率是\(P_A\)。此时想要达到\(SS_A\)还得加上两个相应字符,概率是\(P_A \times \frac{1}{2^2}\)
-
\(S\)以\(T\)结尾,那么加上\(TH\),\(B\)获胜,概率\(P_B\),但是要达到终末态还得再补一个,概率就是\(P_B\times \frac{1}{2}\)
-
其他(比如以\(H\)结尾),那就加上一个\(S_A\),概率是\(P_A\)
而结合两个角度描述同一变化,我们可以得到
同理,\(S \to SS_B\)还有一个方程
但是一共有三个未知数,还差一个方程
这时候再结合题意可知获胜是互斥的,所以
即可求解
接下来我们尝试用字母一般化方程
左边好办,就是多了一个\(\frac{1}{\large2^{len_A}}\),结合题意得到左边都是
对于右边,比如是达到\(A\)必胜状态的话,我们发现,这与\(S\)的后缀能与\(S_A\)的前缀匹配多少的问题,如果匹配了\(a\)长度,那么\(P_A\)的系数就是\(\frac{1}{2^{m-a}}\),但是对于\(S\)的后缀并不好求,那该如何呢?
这里,我们可以借助\(B\)来“枚举”\(S\)的后缀,大不了就是第三种情况,所以就变成了\(B\)的前缀和\(A\)的后缀能匹配多少的问题了,同理可用\(A\)枚举后缀,用什么枚举,就是对应的\(P\)的系数
设\(qian(S,l)\)表示字符串\(S\)的前\(l\)位,\(hou(S,L)\)表示字符串\(S\)的后\(l\)位,那么,第一个方程式右边可以写成
有了这个思路,就能扩展了
对于\(x_i\),我们就用所有猜的串枚举后缀,根据匹配情况决定系数,匹配的就是\(qian(x_i,a)\)
所以第\(i\)个方程长
再有一个
就能解决了
\(n+1\)个方程,\(n + 1\)个未知数(\(x_1 \sim x_n,P_S\))
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++)
{
scanf("%s",s + 1);
for(int j = 1;j <= m;j++)
{
qian[i][j] = qian[i][j - 1] * base + s[j] - 'A';//第i个串的前j位
}
ll o = 1;
for(int j = 1;j <= m;j++)
{
hou[i][j] = hou[i][j - 1] + (s[m - j + 1] - 'A') * o;//第i个串的后j位
o *= base;//这里因为是后缀所以后遍历到的对应的幂次反而大
}
}
twopow[0] = 1; // 1 / (2^k)
for(int i = 1;i <= m;i++) twopow[i] = twopow[i - 1] * 0.5;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
for(int l = 1;l <= m;l++)
{
if(qian[i][l] == hou[j][l]) a[i][j] += twopow[m - l];//处理系数
}
}
a[i][n + 1] = -1.0 * twopow[m];//把P_S移项
a[n + 1][i] = 1;//最后一个方程各未知数(除了P_S)系数均为1
}
a[n + 1][n + 2] = 1;
n++;//n+1个方程
gauss();
for(int i = 2;i <= n;i++) printf("%.10lf\n",a[i][n + 1]);//这个范围是我输出了所有未知数的值后才得到的范围:[2,n+1]
return 0;
}
太tm牛逼了直接给我neng死了
[ABC263E] Sugoroku 3
设\(dp_i\)表示\(i \to n\)的期望
假设摇到了\(j \in [0,A_i]\)
不管\(j\)是多少,次数百分百会\(+1\)
又因为\(i + j\)都可以是目标点
那么可得
化简
后面的\(\sum\)用后缀和来维护
记得疯狂取模,不然会得到\(66 \sim 86\)不等
for(int i = n - 1;i >= 1;i--)
{
dp[i] = ((A[i] + 1) * inv(A[i]) % mod + (sum[i + 1] - sum[i + A[i] + 1]) * inv(A[i]) % mod) % mod;
sum[i] = (sum[i + 1] + dp[i]) % mod;
}
printf("%lld",(dp[1] % mod + mod) % mod);
ABC323E Playlist
\(dp\)
设\(dp_{i,j}\)表示在第\(i\)时刻恰好放完第\(j\)首歌的概率
那么要让第一首歌覆盖\(x + 0.5\)这个点,那么时长这个区间的后端点最小是\(x + 1\),最大是\(x + A_1\)(此时前段正好是\(x\),刚刚盖上)
所以答案是\(\sum\limits_{i=x + 1}^{x + A_1}dp_{i,1}\)
然后剩下的前面的空区间就用其他歌去填满就行了
一开始想了半天,后来才发现是个完全背包
后面的求和拿前缀和维护就行了
[cf261B]Maxim and Restaurant
和上一道题很像,也是用背包,这里是用背包求出方案数在乘以权值搞期望
定义\(dp_{i,j,k}\)表示前\(i\)个人进去了\(j\)个,占据的空间为\(k\)
那么,对于第\(i\)个人,她可能在店内,也可能在店外,两种情况的方案和就是总方案
但背包只是在拿大小说话,没有考虑排列,那么真正的方案数应当是\(dp_{i,j,k} \times j! \times (n - j - 1)!\)
为什么减一呢?这里就是另一个关键——对人进行排列的时候,堵门的人肯定不能动,不然后面的可能换到了门口就能进去了,和\(dp\)数组是不对应的
那么实际上,每一个\(dp\)都对应了一个堵门的人,这个人需要枚举,只有当枚举的这个人在该\(dp\)下能堵住门,即\(a_{du} + k > p\),该\(dp\)和对应的系数这个整体才是答案的一部分


 浙公网安备 33010602011771号
浙公网安备 33010602011771号