1514. 概率最大的路径(最大堆+dijkstral)

1514. 概率最大的路径

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

 

示例 1：

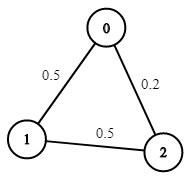
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2：

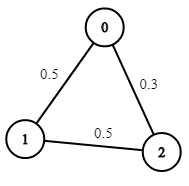
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000

示例 3：

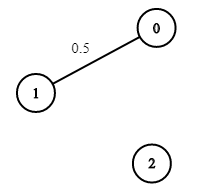
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

 

提示：

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• 每两个节点之间最多有一条边

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        // 1、采用邻接表构建无向图
        vector<vector<std::pair<int, double>>> graph(n); // pair对(终点,起点到终点成功概率值)
        for (unsigned int i = 0; i < edges.size(); i++) {
            auto &edge = edges[i];
            graph[edge[0]].emplace_back(edge[1], succProb[i]);
            graph[edge[1]].emplace_back(edge[0], succProb[i]);
        }
        // 2、采用优先队列保存pair对(起点到终点成功概率值,终点)
        vector<double> prob(n, 0.0); // 存储起点到各点的成功概率值,初始化概率为最小值
        prob[start] = 1.0; // 初始化起点到起点的成功率为1
        priority_queue<std::pair<int, double>> q; // 默认采用最大堆
        q.emplace(start, 1.0); // 起点入队
        while (!q.empty()) {
            auto [curNode, curProb] = q.top(); // 当前节点信息[顶点, 边]->[当前节点, 起点到该节点的成功概率]
            q.pop();
            if (curProb < prob[curNode]) { /* 如果存储的概率已经大于当前概率, 跳过节点 */
                continue;
            }
            /* 从curNode更新相邻节点nextNode的最大概率 */
            for (auto [nextNode, nextProb] : graph[curNode] ) {
                if (prob[nextNode] < prob[curNode] * nextProb) {
                    prob[nextNode] = prob[curNode] * nextProb;
                    q.emplace(nextNode, prob[nextNode]);
                }
            }    
        }
        return prob[end];
    }
};