310. 最小高度树（拓扑+BFS）

310. 最小高度树

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

 

示例 1：

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

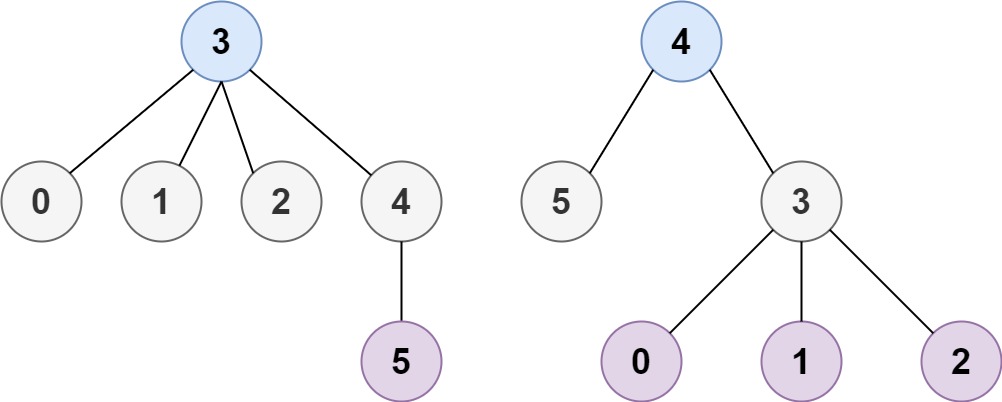
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

 

提示：

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• 所有 (ai, bi) 互不相同
• 给定的输入 保证 是一棵树，并且 不会有重复的边

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        vector<int> res;
        if (n == 1) {
            return {0};
        }
        // 构建图和节点度
        vector<int> degree(n, 0);
        vector<vector<int>> graph(n);
        for (auto &edge : edges) {
            degree[edge[0]]++;
            degree[edge[1]]++;
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        queue<int> q;
        // 叶子节点入队
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1) {
                q.push(i);
            }
        }
        // BFS从各个叶子节点出发
        while (!q.empty()) {
            int size = q.size();
            res.clear();
            for (int i = 0; i < size; i++) {
                int curNode = q.front();
                q.pop();
                res.push_back(curNode);
                // 剪枝
                degree[curNode]--;
                // 找出与当前节点相邻节点,如果相邻节点度为1表示该相邻节点为新的叶子节点并入队
                for (auto &node : graph[curNode]) {
                    degree[node]--;
                    if (degree[node] == 1) {
                        q.push(node);
                    }
                }
            }
        }
        return res;
    }
};