题解 luogu.P2675 《瞿葩的数字游戏》T3-三角圣地

题目

luogu.P2675 《瞿葩的数字游戏》T3-三角圣地

题意建模

一道比较隐晦，但是很有价值的好题，融合了贪心思想的最优化构造以及组合数学的计数。我们主要是讨论一下这道题的贪心具体的细节。因为笔者恰好就是卡在了贪心的构造和证明上。

算法分析

拿到题面，一看就是杨辉三角。我们手搓几个样例：

当 \(n=5\) 时：按照直观感受，可以有如下样例。

当然，交换一下两边，还是 \(61\)，答案是不变的。还有没有其它情况呢？假设这个最大数不在中间呢？又有如下样例：

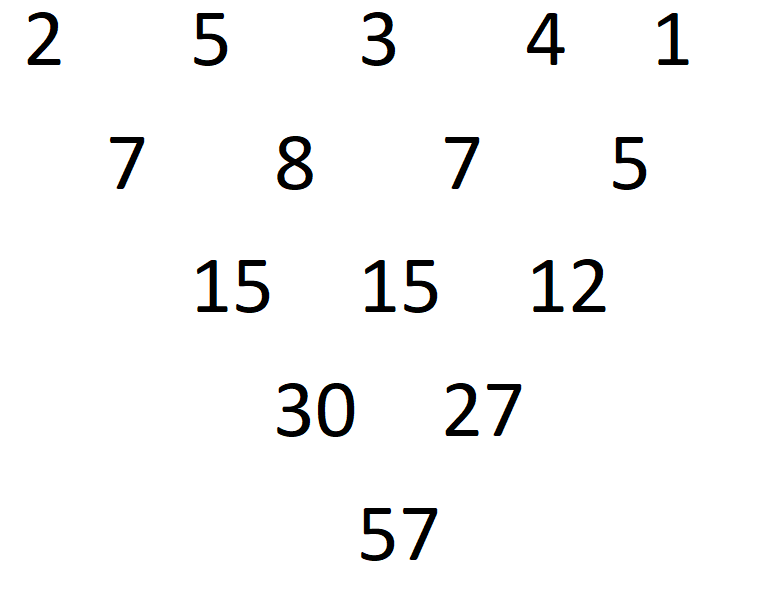
欸，似乎答案变小了。这说明什么？说明我们的直观感受可能是正确的。现在回过头来，我们想一想这个贪心策略是什么？

贪心策略：将一个 \(n\) 的全排列中最大的数放到尽可能靠中间的位置。如果 \(n=2k+1,k \in Z\)，那么肯定就是在最中间；如果 \(n=2k,k \in Z\)，那么就是最大数和次大数放在 $ \lfloor n/2 \rfloor$ 到 \(\lceil n/2 \rceil\) 之间。

为啥这样是对的？首先一个不证自明的基本事实是：越大的数被运算累加的次数越多，贡献越大。然后，可以有杨辉三角得出结论：对于 \(1≤i≤n，val_{i}= C(n-i,i-1)\)

现在的难点就是如何构造这种最优解的情况。用什么数据结构呢？最好是有单调性的，并且是可以模拟这个大数在中间，小数在两边，并且近似对称分布的一种结构。

有了！栈和双端队列的结合！为啥？

• 栈，满足 FILO 的性质，可以使大数在上；

• 双端队列，两边都可以插入元素，这样先插进的元素来自于栈顶，较大，所以较为在中间。

刚好满足特性！

开始编码！

参考代码

#include<iostream>
#include<deque>
#include<stack>
#define rei register int
using namespace std;
using ll=long long;
const int N=1e6+5,mod=10007;
stack<int> s;
deque<int> q;
int fac[N];
ll ans;
ll fpow(ll x,ll y,int p)
{
	ll res=1;
	while(y)
	{
		if(y&1) (res*=x)%=p;
		(x*=x)%=p;
		y>>=1;
	}
	return res;
}
ll C(ll n,ll m,int p)
{
	if(n<m) return 0;
	if(m>n-m) m=n-m;
	/*ll f=1,g=1;
	for(int i=1;i<=m;i++)
	{
		(f*=n-i+1)%=p;
		(g*=i)%=p;
	}
	return f*fpow(g,p-2,p)%p;*/
	return fac[n]*fpow(fac[n-m],p-2,p)%p*fpow(fac[m],p-2,p)%p;
}
ll lucas(int n,int m,int p)
{
	if(m==0) return 1;
	return C(n%p,m%p,p)*lucas(n/p,m/p,p)%p;
}
int main()
{
	int n; cin>>n;
	for(rei i=1;i<=n;i++) s.push(i);
	fac[0]=1;
	for(rei i=1;i<=n;i++)
		fac[i]=fac[i-1]*i%mod;
	while(s.size())
	{
		q.push_back(s.top());
		s.pop();
		if(s.size())
		{
			q.push_front(s.top());
			s.pop();
		}
	}
	for(int i=1;i<=n;i++)
	{
		(ans+=lucas(n-1,i-1,mod)*q.front())%=mod;
		q.pop_front();
	}
	cout<<ans<<endl;
	return 0;
}

细节实现

还好，细节不多，我们也没有讨论组合计数的内容。的确，确实是一个比较综合的题目。

笔者的重点还是放在了贪心上，以及基本的数据结构。

总结归纳

再接再厉！