题解 luogu.P4388 付公主的矩形

题目

luogu.P4388 付公主的矩形

一道好题。思维含量比较大。

题意建模

关于本题，是考察 \(\gcd\) 的。但是，遗憾的是，我没有看出来。

算法分析

初步理解

首先，很显然的，我不知道如何去找这个题矩形和 GCD 的关系。恰恰是本题的难点。

想着仔细分析一下样例吧，如图所示：

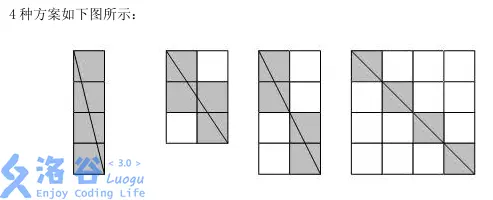
似乎有什么性质，但是没有挖掘出来。。定睛一看：好像是有这么一条性质吧？

\[\gcd(n,m)=1 \Leftrightarrow \text{对角线不经过格点} \]

感觉看到了曙光。继续分析，再画几个图分析一下。好像的确如此。为甚？这个留到细节研讨的时候我去证明。现在先按下不表。

继续分析：既然有了这么一条性质，下步要干啥呢？

参考代码

#include<iostream>
#include<cstring>
#define rei register int
using namespace std;
const int N=1e6+5;
int pri[N/5],phi[N],idx;
bool is_pri[N];
int ans;
void get_phi(int n)
{
	memset(is_pri,true,sizeof(is_pri));
	is_pri[0]=is_pri[1]=false;
	phi[1]=1;
	for(int i=2;i<=n;++i)
	{
		if(is_pri[i]) pri[++idx]=i,phi[i]=i-1;
		for(int j=1;i*pri[j]<=n;++j)
		{
			int temp=i*pri[j];
			is_pri[temp]=false;
			if(i%pri[j]==0) 
			{
				phi[temp]=phi[i]*pri[j];
				break;
			}
			else phi[temp]=phi[i]*(pri[j]-1);
		}
	}
}
int main()
{
	int n; cin>>n;
	get_phi(n+1);
	for(int i=2;i<=n;i++)
		if(!(n%i)) ans+=(phi[i+1]>>1);
	cout<<++ans<<endl;
	return 0;
}

细节实现

关于上述结论正确性的讨论。

命题

\[\gcd(n,m)=1 \Leftrightarrow \text{对角线不经过格点} \]

证明

引理1

相似形的边对应成比例。

引理2

相似矩形的对角线在重合顶点时，是重合的。

引理属于平凡的结论，初等几何中是涉及到了的，这里不再赘述。主要解释一下什么叫“重合顶点”。这个概念是笔者引入的，可以参见下面任意一图中有细线勾勒成的小矩形。这可以知道答案。

下证：

充分性

考虑使用反证法。假设 \(\gcd(n,m)\neq 1\)，那么设 \(d=gcd(n,m)\)，那么也就是很显然有：

\[d\mid n,d\mid m \]

由引理及上述假设知，一定存在一个相似形（这里是矩形），那么两个矩形的对角线是必定重合的（这个结论是平凡的）。由假设，矛盾，故而充分性成立；

必要性

原命题右边部分的等价的表述是：

至少存在一个顶点被矩形的对角线所经过

考虑使用解析几何的工具。建立笛卡尔坐标系，使大矩形的边与横纵坐标轴平行。向该格点作坐标轴的铅垂线，那么，易知存在相似图形。剩余论述同上，下面给出参考图：

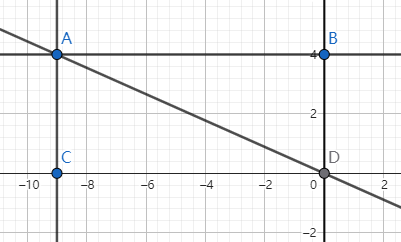
图1：这是没有经过格点的矩形；

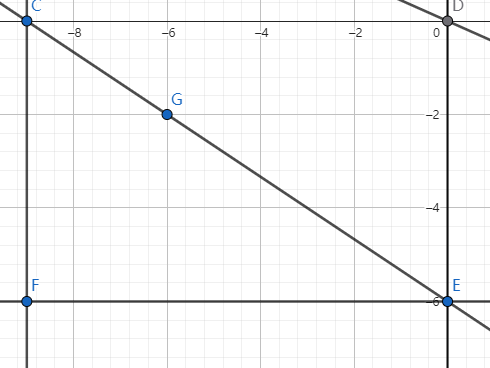
图2：这是经过了格点（\(G\)）的矩形。

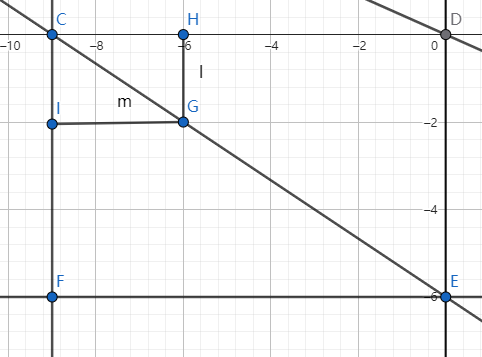
图3：更进一步地，显然有 $ \text{矩形}CHGI\sim \text{矩形}CDEF$ 。

总结归纳

由于做法笔者没有完全摸清，先放着，正思考中。