题解 luogu.P2290 [HNOI2004] 树的计数

题目

luogu.P2290 [HNOI2004] 树的计数

本题可看作是 Prüfer 序列的一道模板题。

题意建模

首先来介绍一下什么是 Prüfer 序列。

定义

标号树的 Prüfer 序列是由树唯一地产生的序列。更具体地，Prüfer 序列可以将一个带标号 \(n\) 个节点的无根树用 \([1,n]\) 中的 \(n−2\) 个整数表示。

建立

每次选择一个编号最小的叶节点并删掉它，然后在序列中记录它连接到的那个节点，重复 \(n−2\) 次后就只剩下两个节点，就结束了。

下面是一个样例的模拟过程。

例如，这是一棵 7 个结点的树的 Prüfer 序列构建过程：

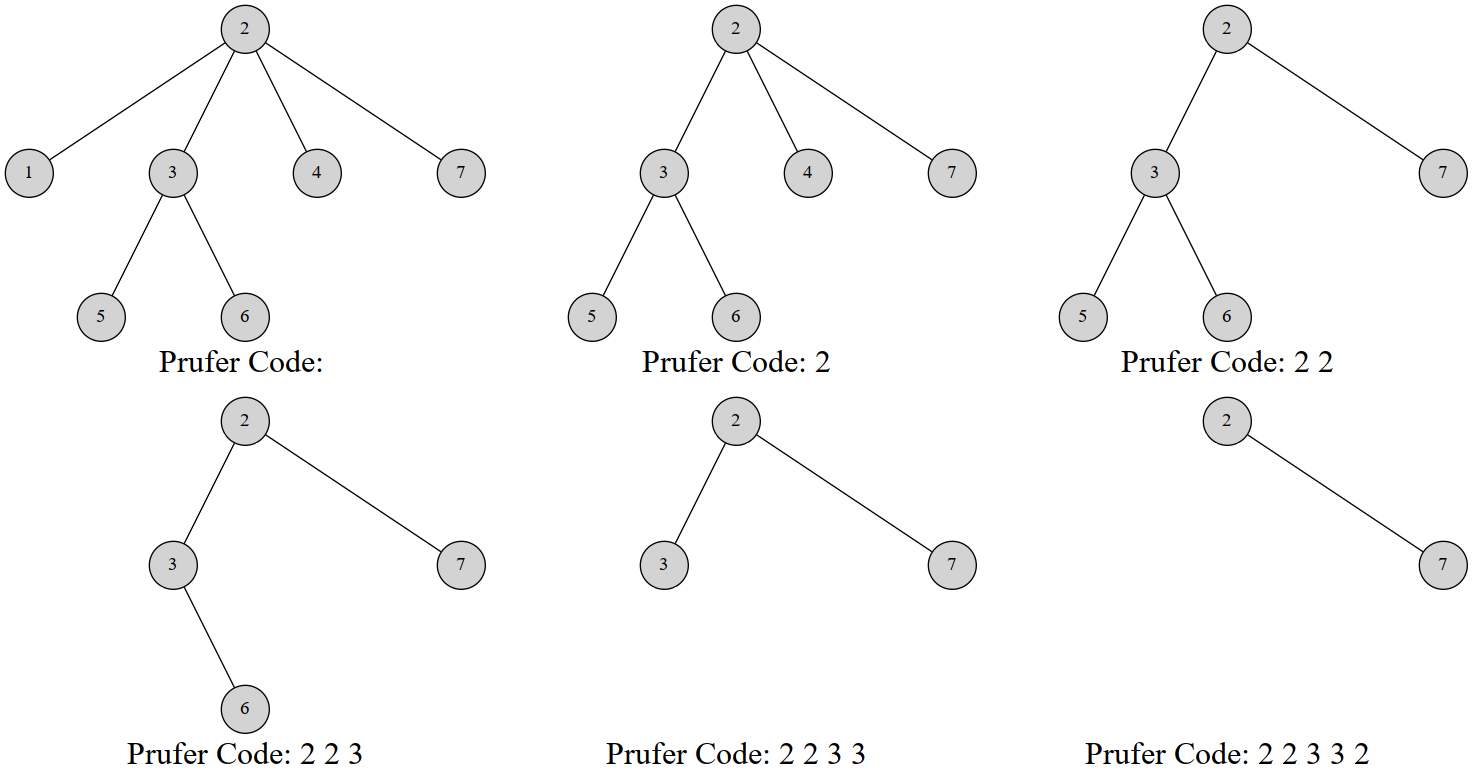
最终的序列就是 \(2,2,3,3,2\)。

当然，也有一个线性的构造算法。不过我们不过多讨论。

性质

由于这里是组合数学的应用，笔者不会过多介绍这个 Prüfer 序列在图论当中的应用，而只会说明该序列在组合计数中的运用。

• 一棵树的序列明显是确定的，而且长为 \(n − 2\)；

• 每个节点在序列中出现的次数是其度数减 \(1\)。

知道了这些结论，本题就是一个模板题了。

算法分析

我们给出答案：

设节点 \(i\) 的度数为 \(d_{i}\)，那么本题总的数量应为：

\[\frac{(n-2)!}{\prod_{i=1}^{n}(d_{i}-1)!} \]

首先，我们先前介绍了性质 \(1\)，\(2\)。这两条性质其实提示我们，这是一个可重复集合的排列。所以有可重集排列的定理推得以上公式。

至于具体的代码实现，这里就不是很难了。就变成一个数论问题，分解质因数然后约分即可。

参考代码

#include<iostream>
#define rei register int
using namespace std;
using ll=long long;
const int N=200;//i!'s factor j,which oucurs times 
int idx,factor[N][N],degree[N];
ll ans,tot;
void get_fac(int n)
{
	int temp=n;
	for(int i=2;i<=n/i;i++)
		if(n%i==0)
		{
			factor[temp][i]++;
			n/=i;
			while(n%i==0) n/=i,factor[temp][i]++;
		}
	if(n>1) factor[temp][n]++;
}
int main()
{
	int n; cin>>n;
	if(n==1)
	{
		cin>>degree[1];
		cout<<(degree[1]?0:1)<<endl;
		return 0;	 
	}
	
	for(rei i=1;i<=n;++i)
	{
		cin>>degree[i];
		tot+=degree[i];
		if(!degree[i]) return cout<<0<<endl,0;
	}
	if(tot!=2*n-2) return cout<<0<<endl,0;
	for(rei i=1;i<=n;++i)
	{
		get_fac(i);
		for(rei j=1;j<=n;j++) 
			factor[i][j]+=factor[i-1][j];
	}
	
	for(rei i=1;i<=n;++i)
		for(rei j=1;j<=n;++j)
			factor[n-2][j]-=factor[degree[i]-1][j];
	
	ans=1;
	for(rei i=1;i<=n;++i)
		if(factor[n-2][i])
			for(ll j=1;j<=factor[n-2][i];j++)
				ans*=i;
	
	cout<<ans<<endl;
	return 0;
}

细节实现

但是这里有一些细节。

• 节点数量问题。
  通常，我们不考虑含有 \(1\) 个结点的树。但是本题显然会出现这种数据。所以需要做出特判。代码中有体现：如果这一个节点的度数为 \(0\)，那么答案为 \(1\)。否则为 \(0\)。

• 解的存在问题。
  当 $\sum_{i=1}^{n}d_{i} \neq 2n-2 $ 时，没有可行解。

总结归纳

初步介绍 Prüfer 序列的一些性质及应用。

参考资料：OI Wiki 、百度百科。