[数据结构] AVL树
AVL树的基本概念
AVL树的定义
AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis。
AVL树本质上是一颗二叉搜索树,并且本身带有平衡的条件,即每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
AVL树可以始终将其高度控制在 ,从而保证AVL树的平衡。
平衡因子
平衡因子(balance factor)指的是一个节点的左右子树的高度差。在AVL树中,任意一个节点的平衡因子绝对值不会超过 1 。
一般情况下,我们将单个节点的高度初始化为1,所以空树高度即为0,而树中叶子节点的高度就为1。在进行节点插入操作后,也将对树的高度进行调整。左右子树的高度是判断当前树是否满足AVL树的标准,所以,在AVL树的节点结构体中,我们还需要加入高度参数 height,同时也需要相对于的取高度函数,这样更加方便。
typedef struct BiNode{
int val;
int height; //需记录每个节点的高度
struct BiNode *left, *right;
}BiNode, *BinaryTree;
//返回节点的高度
int GetHeight(BinaryTree root){
return root ? root->height : 0;
}
失衡与重平衡
在AVL树中插入和删除的操作是根据二叉搜索树的性质来实现的,这样的话可能会导致二叉树高度的变化,从而可能导致节点的左右子树高度差的绝对值大于1,使得不再满足AVL树的性质。我们需要找到最小不平衡子树,然后进行旋转调整,使之再次满足AVL树的性质。
AVL树的旋转方式主要分为单旋和双旋,其中单旋分为 LL型 和 RR型,双旋 分为 LR型 和 RL型 。
在进行完旋转操作之后,还需要对当前最小不平衡子树的根节点的高度进行调整。
AVL树的插入操作时的调整
LL型 右旋
LL型旋转
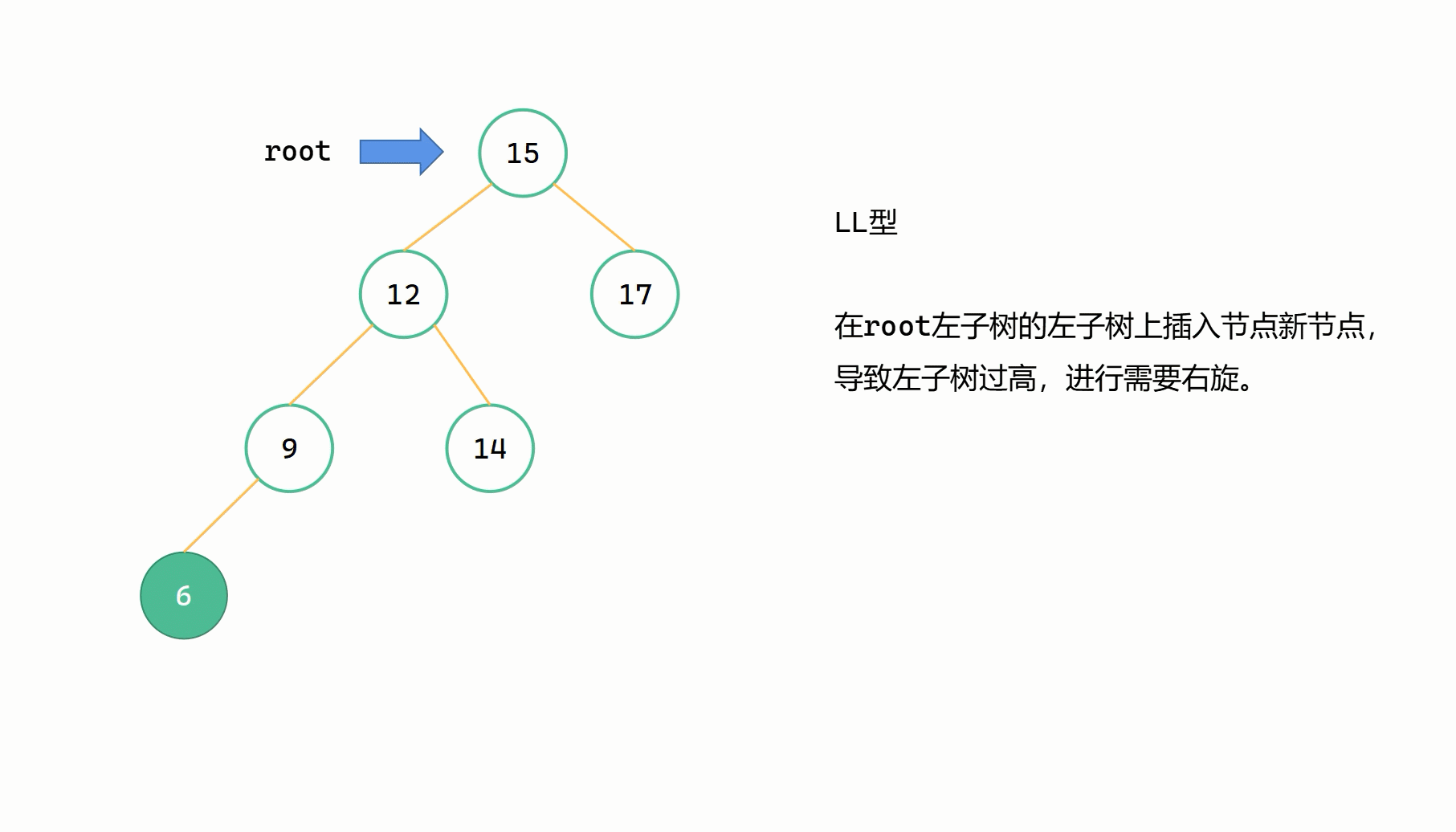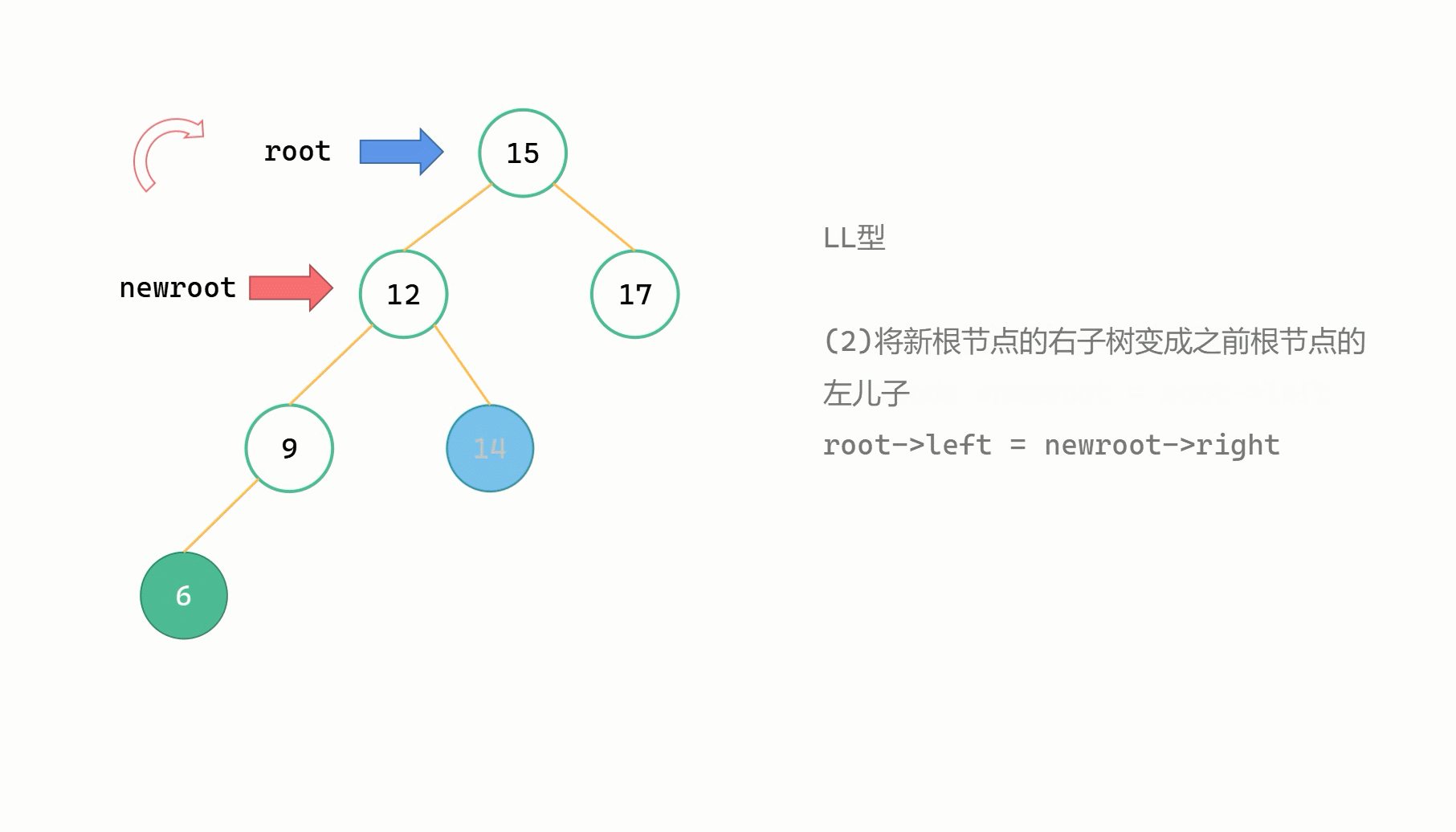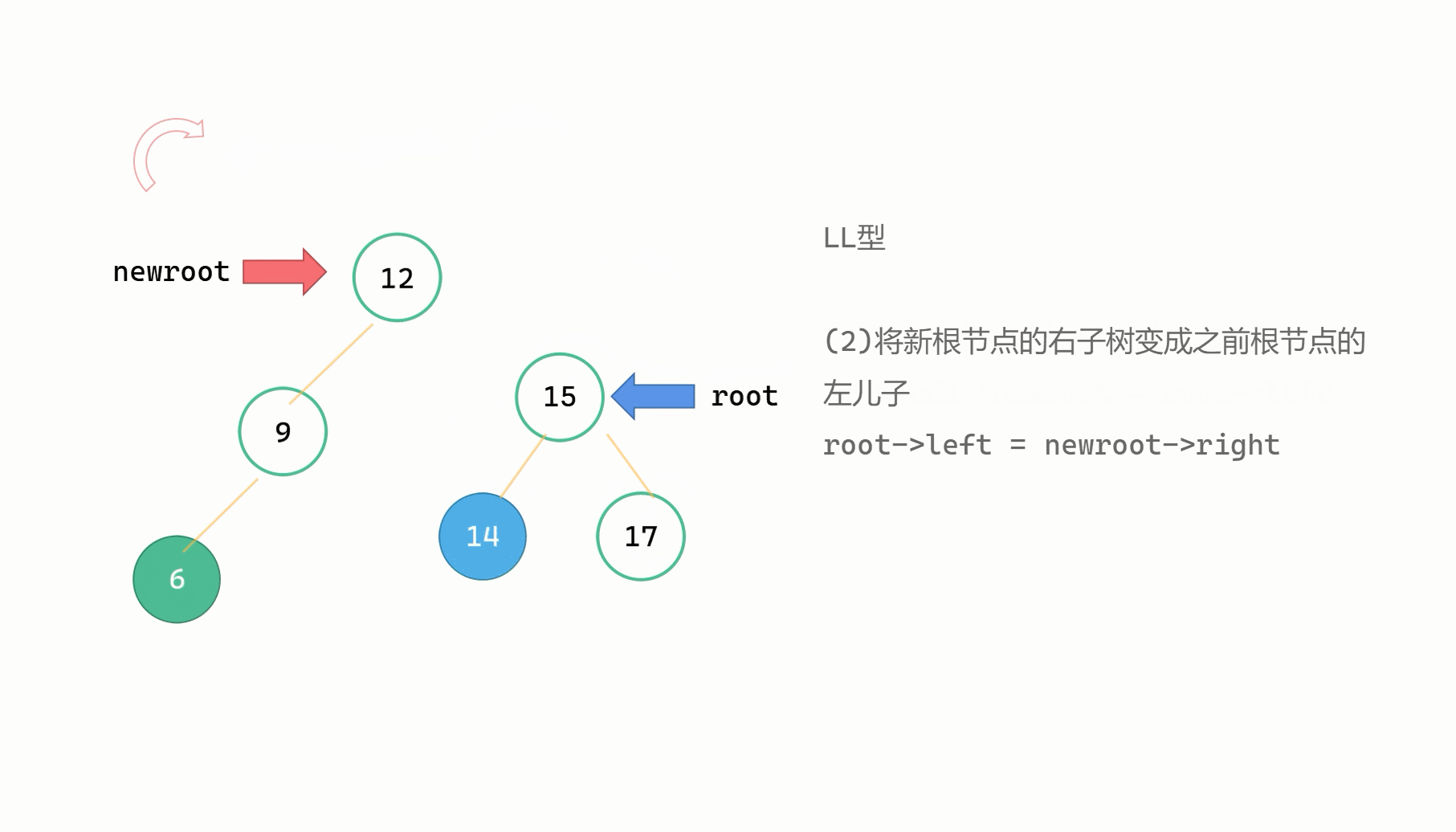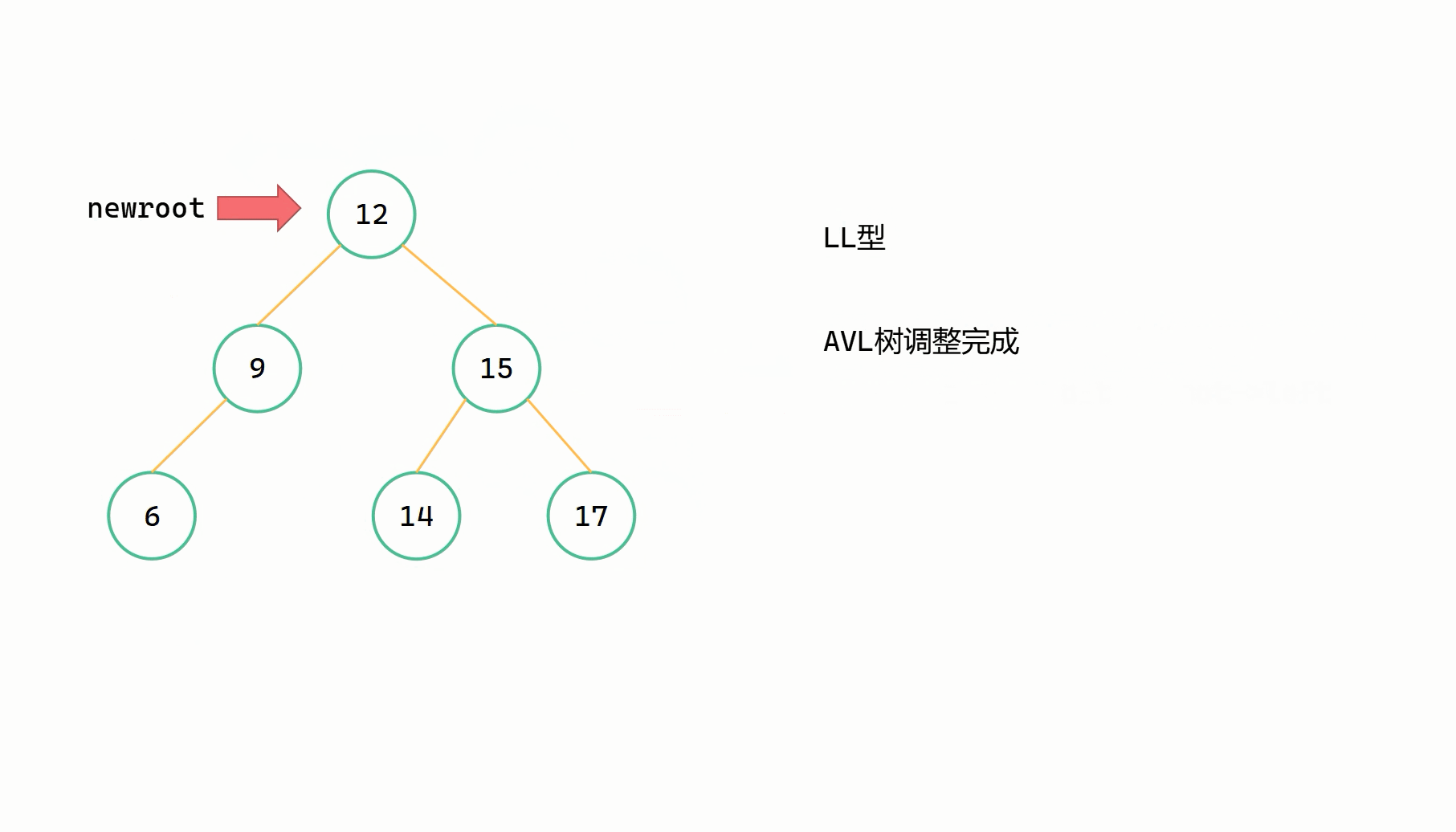
LL型指的是,新插入的节点位于最小不平衡子树的左子树的左子树上的情况,此时因为左子树过高而导致不平衡。此时需要进行右旋,使得子树平衡。
最小不平衡子树的根节点为 root,我们需要将其左儿子作为新的根节点 newroot,并将 root 变成 newroot 的右子树根节点。观感上就是顺时针旋转或者向右旋转,这样可以使得最小不平衡子树的左子树的高度减小,右子树的高度增加,从而达到平衡。
但是,如果说左子树存在右子树,那么在将 root 变成 newroot 的右子树根节点之前,需要将这个右子树先继承给 root ,变成其左子树。这样一定是合法的,因为当前 newroot 后来会变成新的根节点,不再作为 root 的左子树,而且 newroot 的右子树所有节点值满足小于 root 的节点值。故我们可以把 newroot->right 先变成 root->left,再将 root 变成 newroot->right。
大致步骤为:
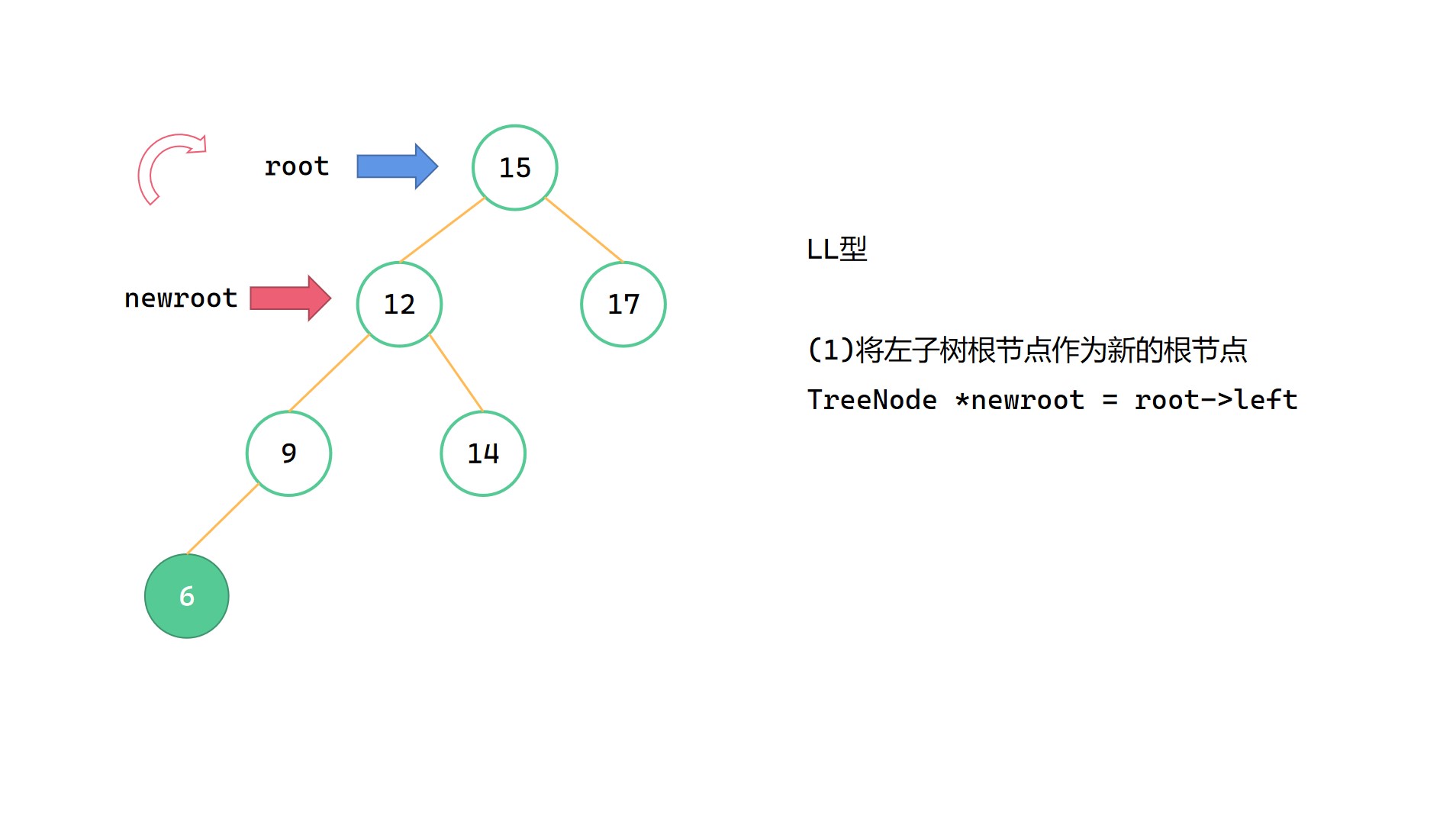
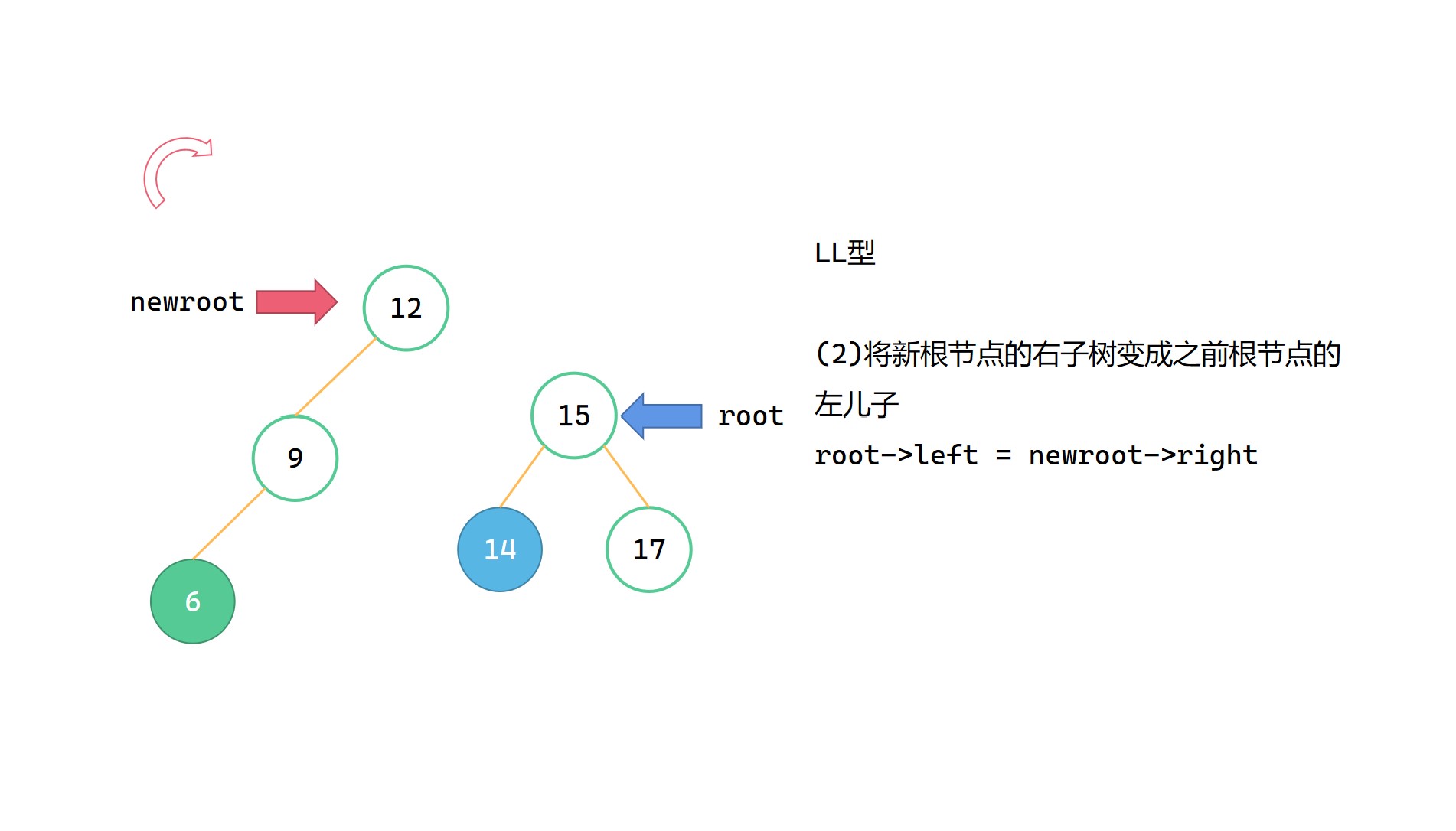
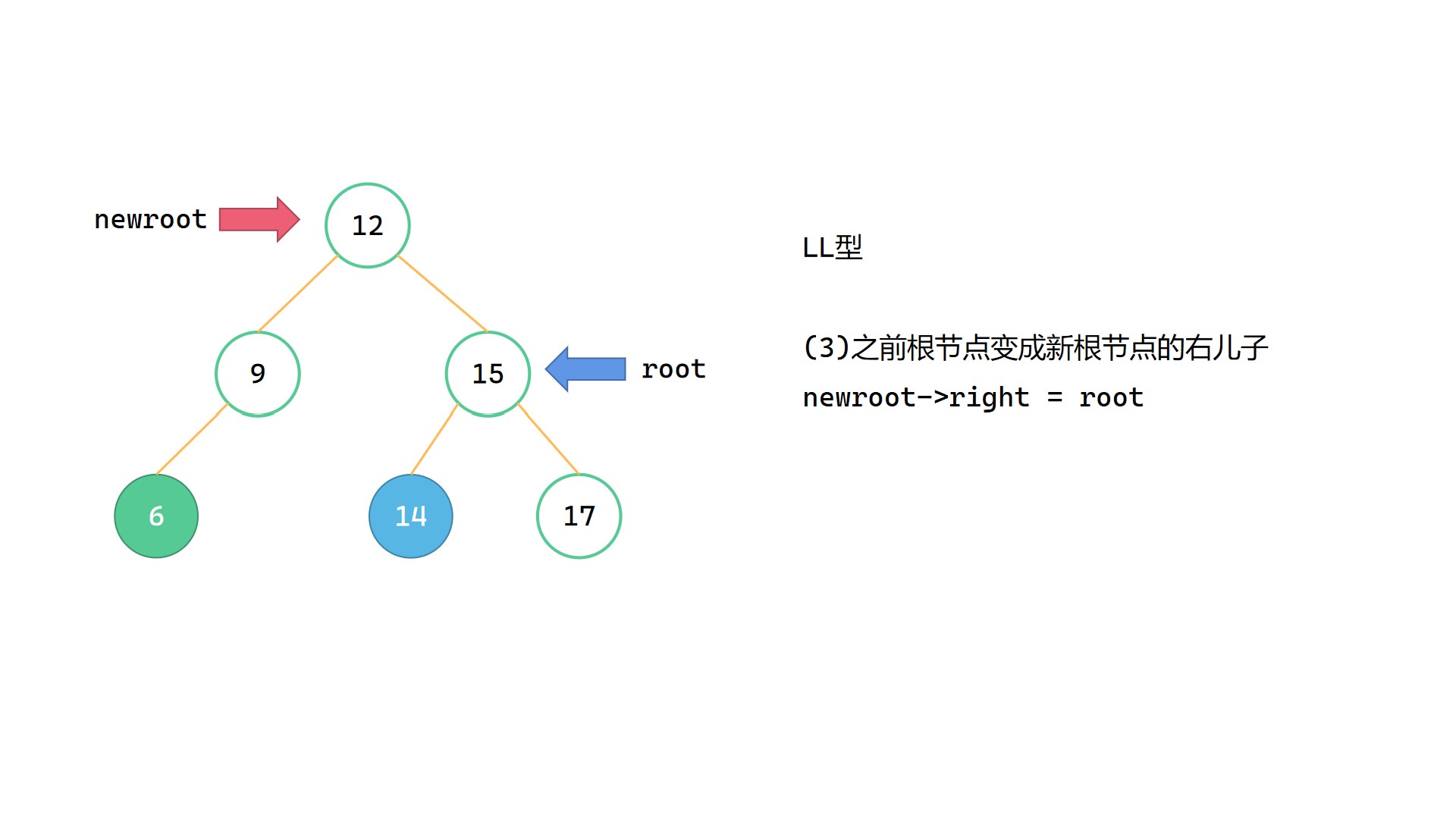
(1)Node newroot = root->left
(2)root->left = newroot->right
(3)newroot->right = root
(4)调整 root, newroot 高度
调整高度只需要更新成取节点左右子树中较大的高度,然后再 +1 就可以了,节点的左右子树高度本质上是没有改变的(此时暂且忽略新插入的节点)。
LL型旋转 图解
动画演示
逐帧图解
(1)

(2)
(3)

(4)
(5)
(6)

LL型旋转 代码
//插入节点位于最小不平衡子树根节点的左儿子的左子树上 LL 进行右旋
BinaryTree LL_rotate(BinaryTree &root){
BinaryTree newroot = root->left; //右旋,左儿子成为新的根节点
root->left = newroot->right; //左儿子的右子树成为根节点的左子树
newroot->right = root; //之前根节点成为新根节点的右子树
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
newroot->height = std::max(GetHeight(newroot->left), GetHeight(newroot->right)) + 1;
return newroot;
}
RR型 左旋
RR型旋转
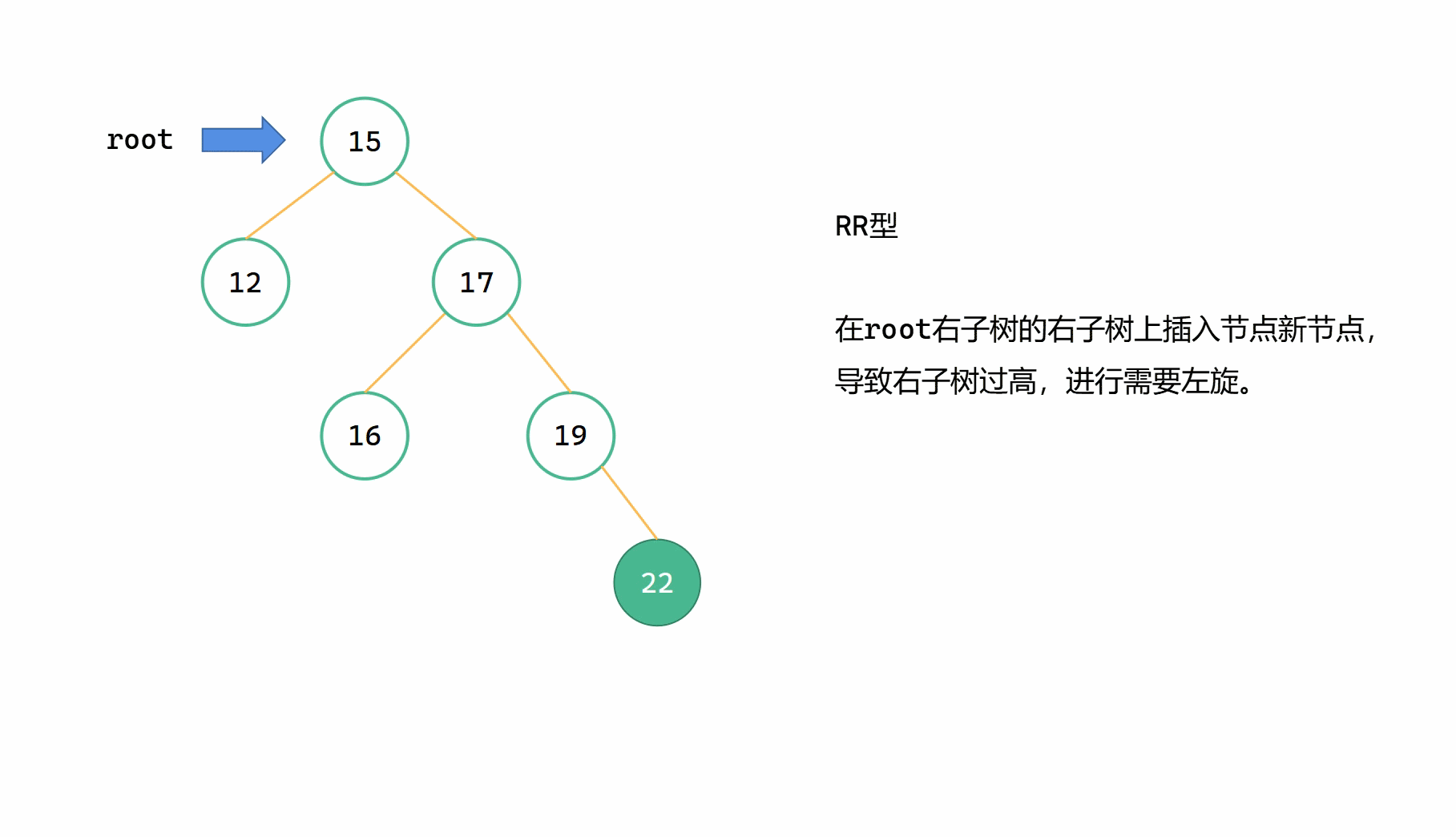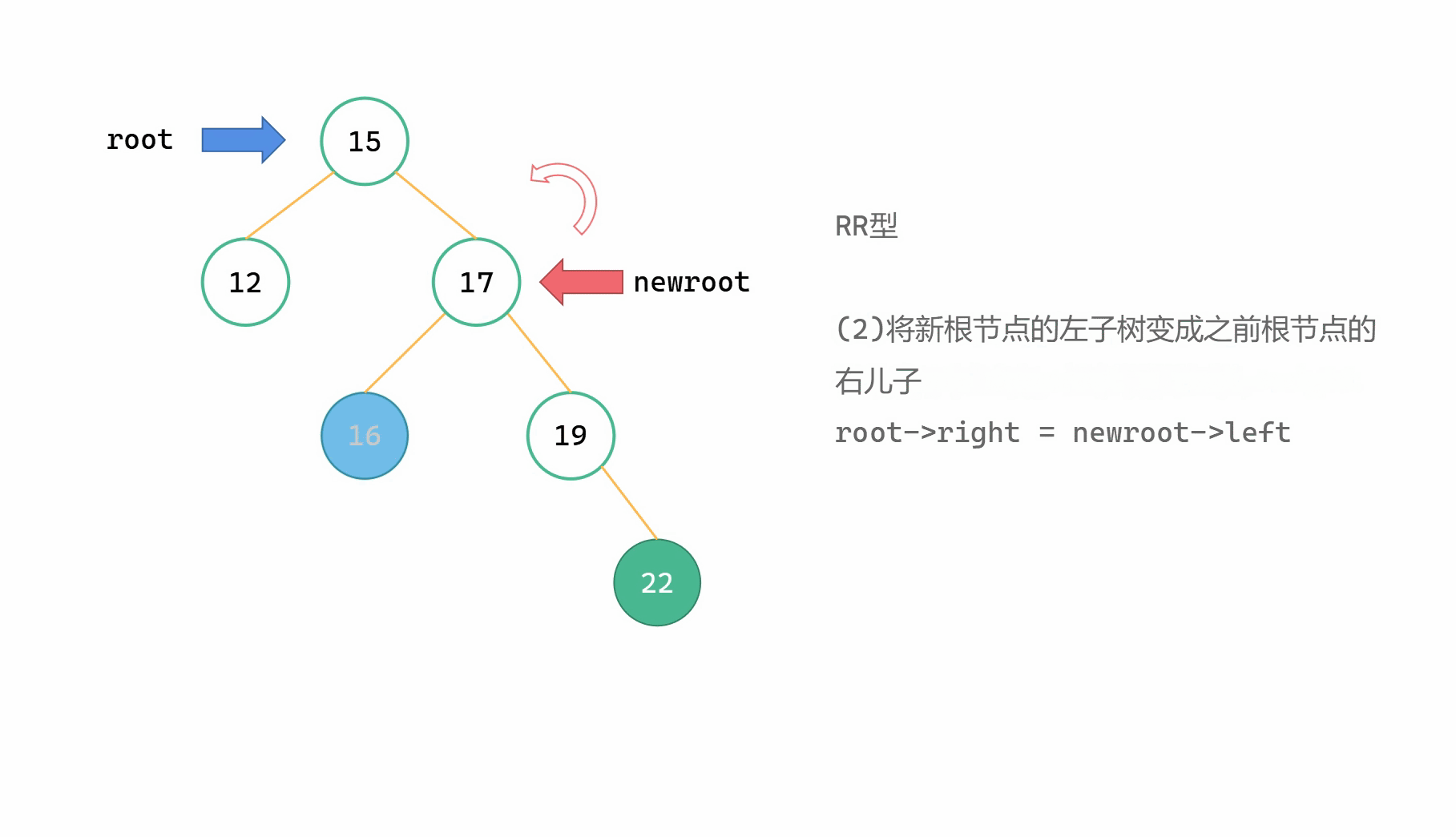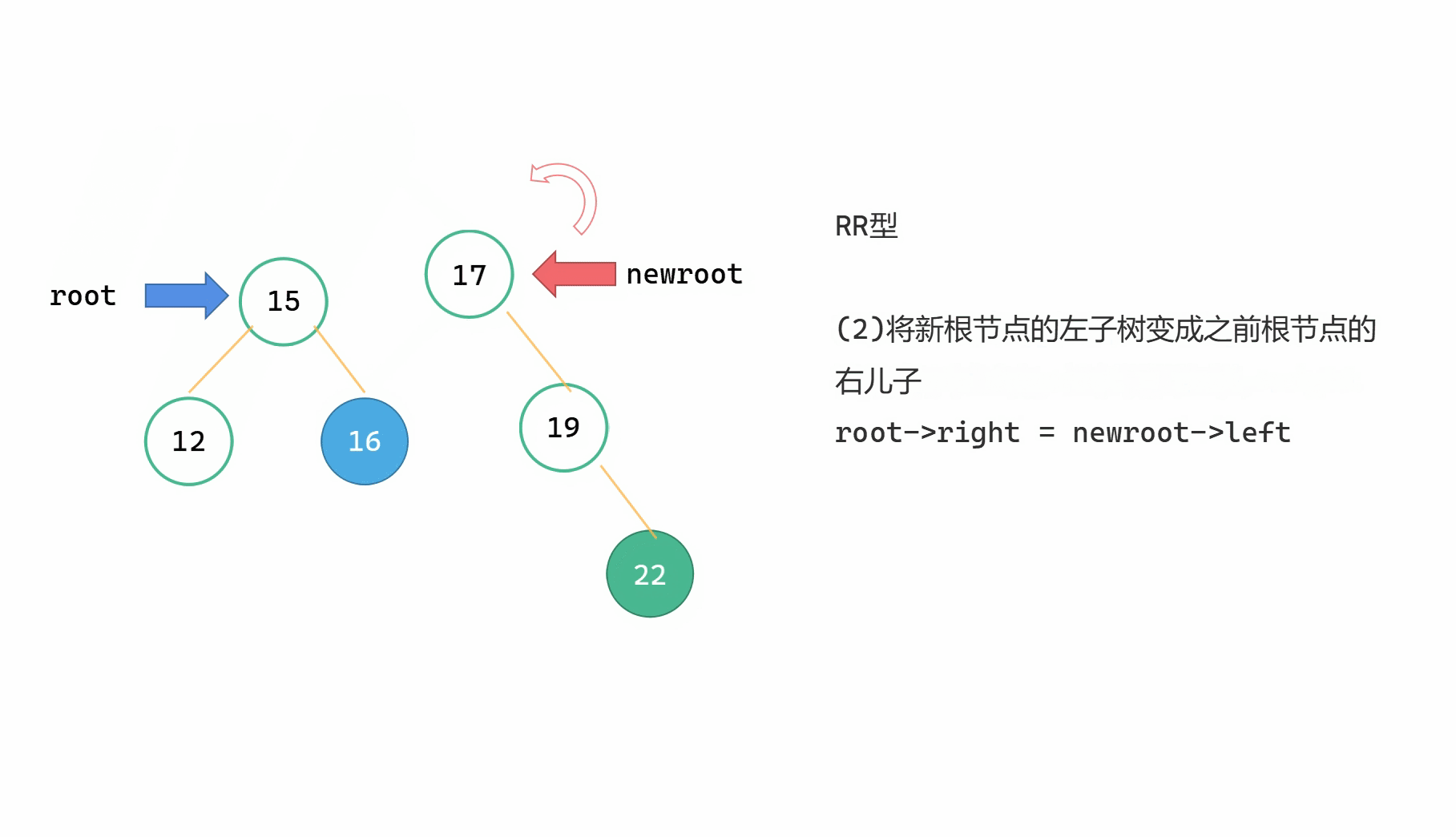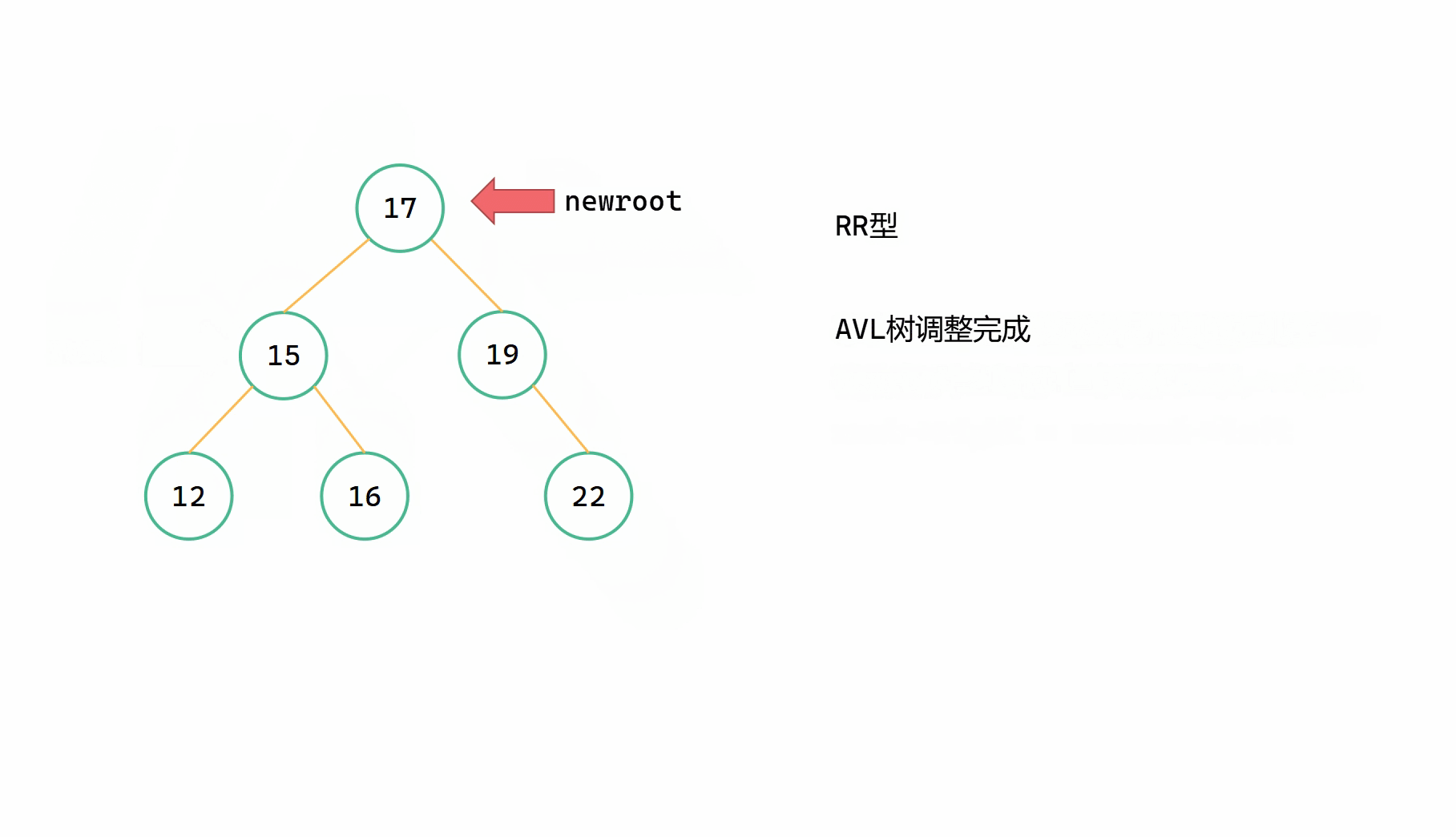
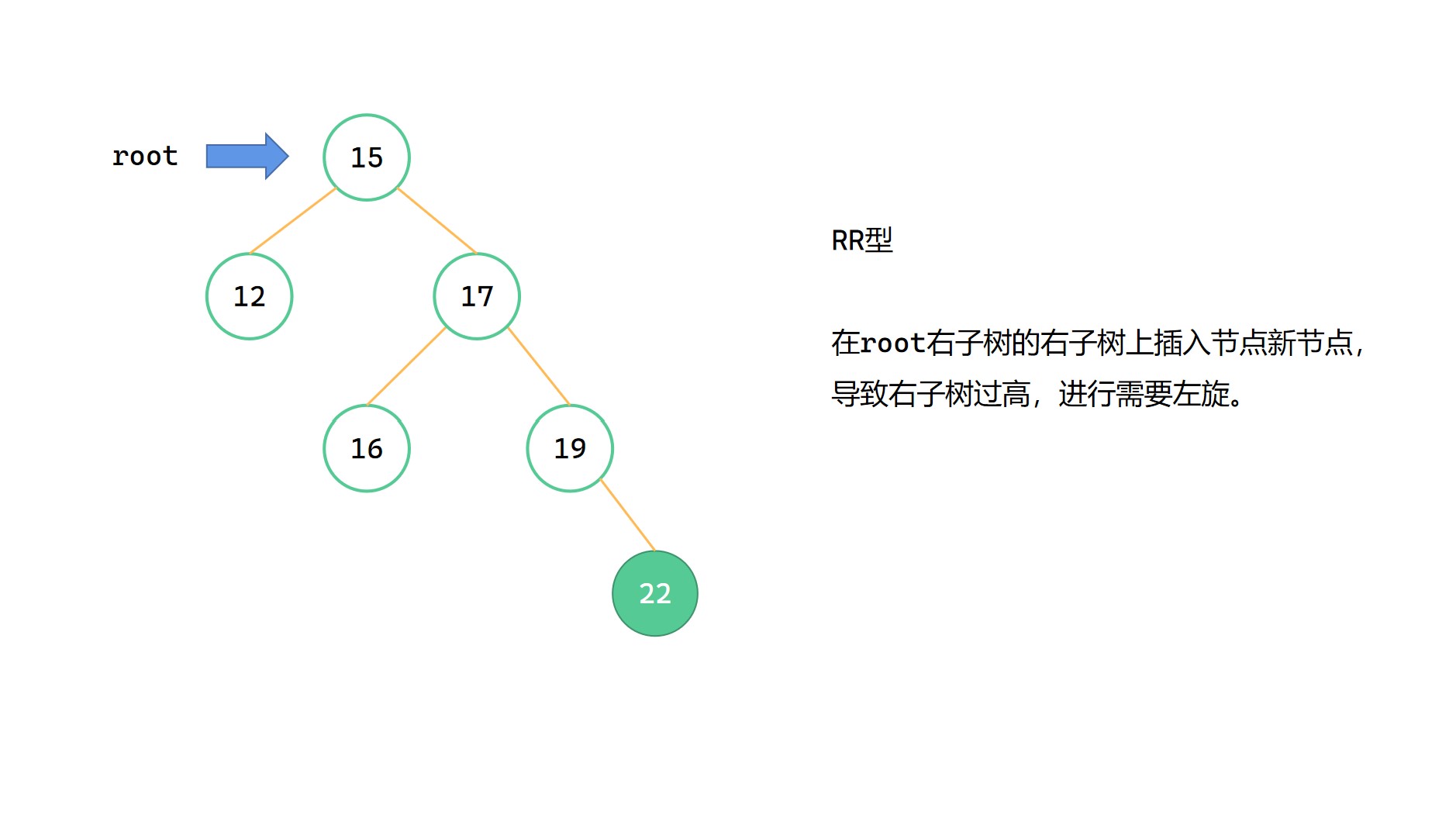
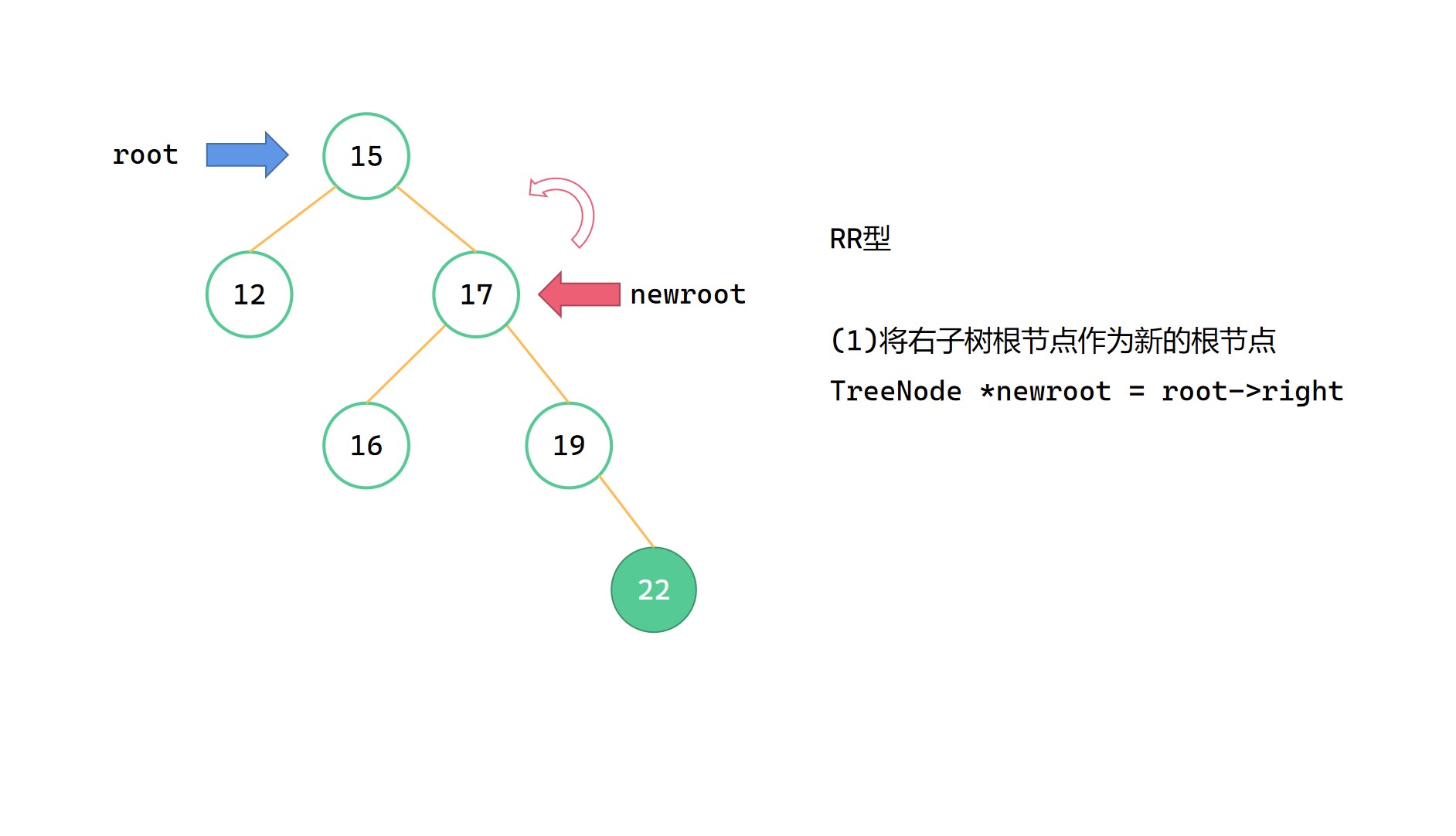
RR型指的是,新插入的节点位于最小不平衡子树的右子树的右子树上的情况,此时因为右子树过高而导致不平衡。此时需要进行左旋,使得子树平衡。
最小不平衡子树的根节点为 root,我们需要将其右儿子作为新的根节点 newroot,并将 root 变成 newroot 的左子树根节点。观感上就是逆时针旋转或者向左旋转,这样可以使得最小不平衡子树的右子树的高度减小,左子树的高度增加,从而达到平衡。
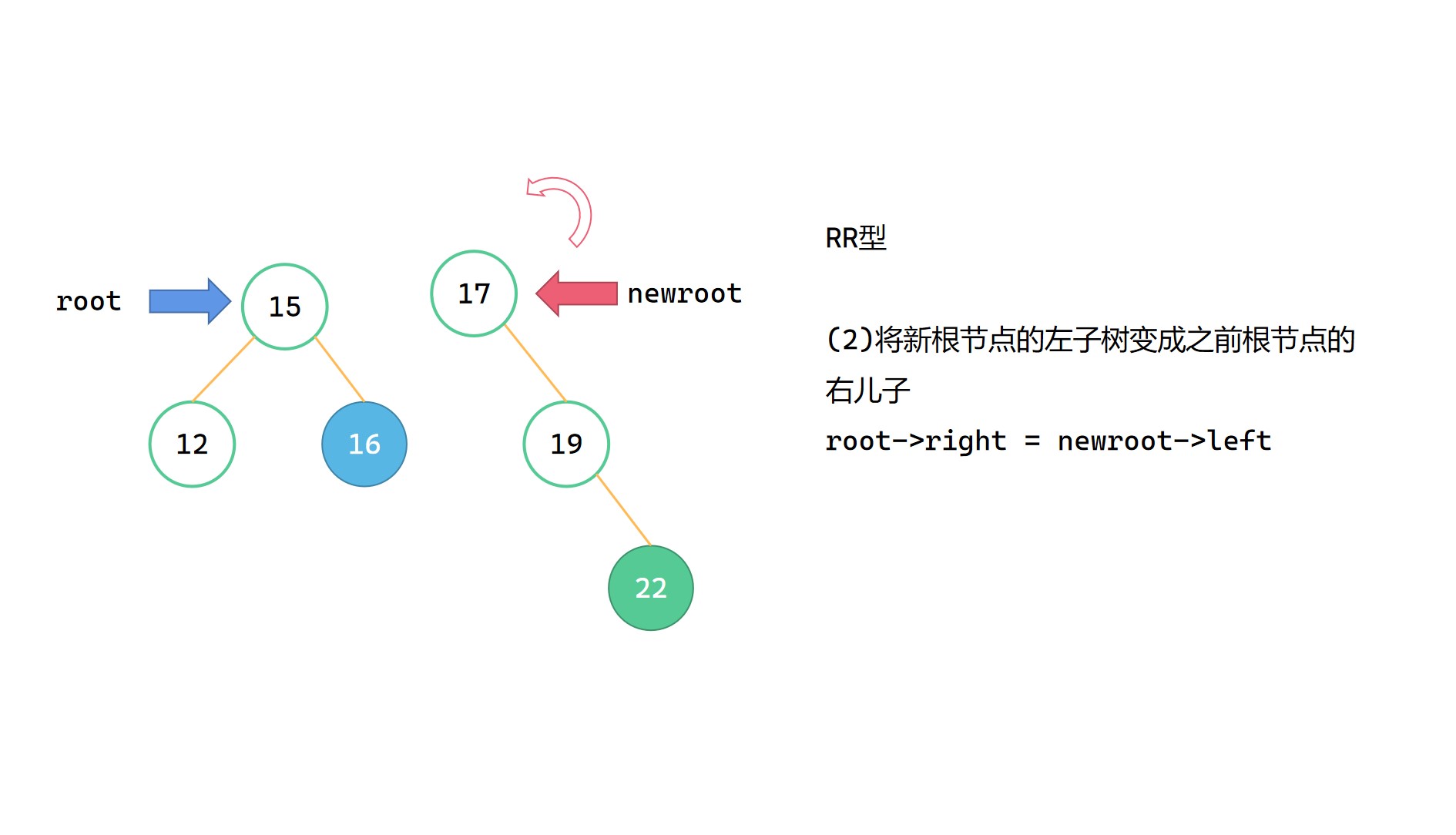
与LL型类似地,如果说右子树有左子树,那么在将 root 变成 newroot 的左子树根节点之前,需要将右子树的左子树先继承给 root ,变成其右子树。当前 newroot 后来会变成新的根节点,不再作为 root 的右子树,而且 newroot 的左子树所有节点值满足大于于 root 的节点值。故我们可以把 newroot->left 先变成 root->right,再将 root 变成 newroot->left。
大致步骤为:
(1)Node newroot = root->right
(2)root->right = newroot->left
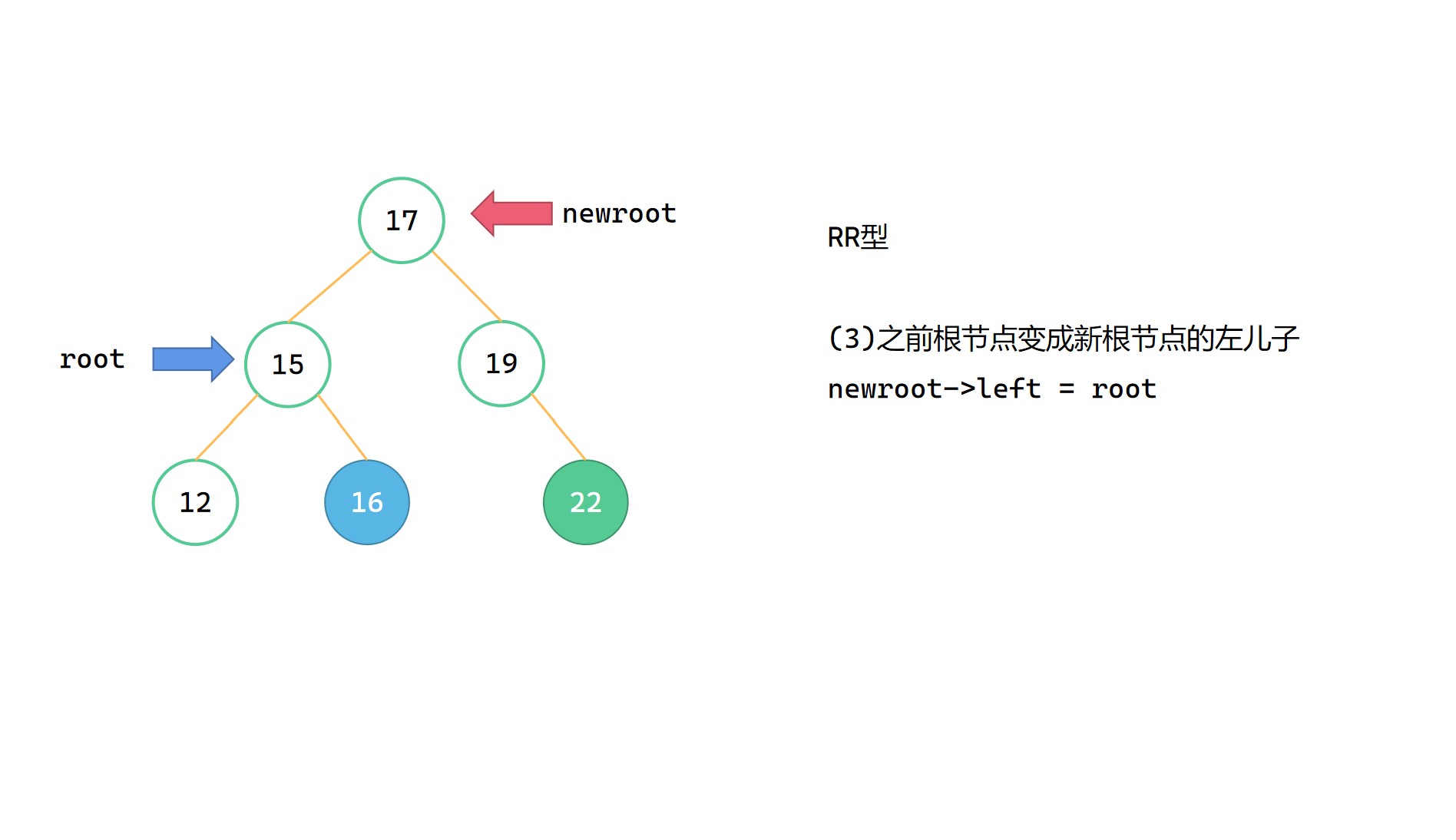
(3)newroot->left = root
(4)调整 root,newroot 高度
RR型旋转 图解
动画演示
逐帧图解
(1)
(2)
(3)

(4)
(5)
(6)

RR型旋转 代码
//插入节点位于最小不平衡子树根节点的右儿子的右子树上 RR 进行左旋
BinaryTree RR_rotate(BinaryTree &root){
BinaryTree newroot = root->right; //左旋,右儿子变成新的根节点
root->right = newroot->left; //右儿子的左子树变成当前根节点的右子树
newroot->left = root; //原先根节点变成新根节点的左子树
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
newroot->height = std::max(GetHeight(newroot->left), GetHeight(newroot->right)) + 1;
return newroot;
}
LR型 先左旋再右旋
LR型旋转
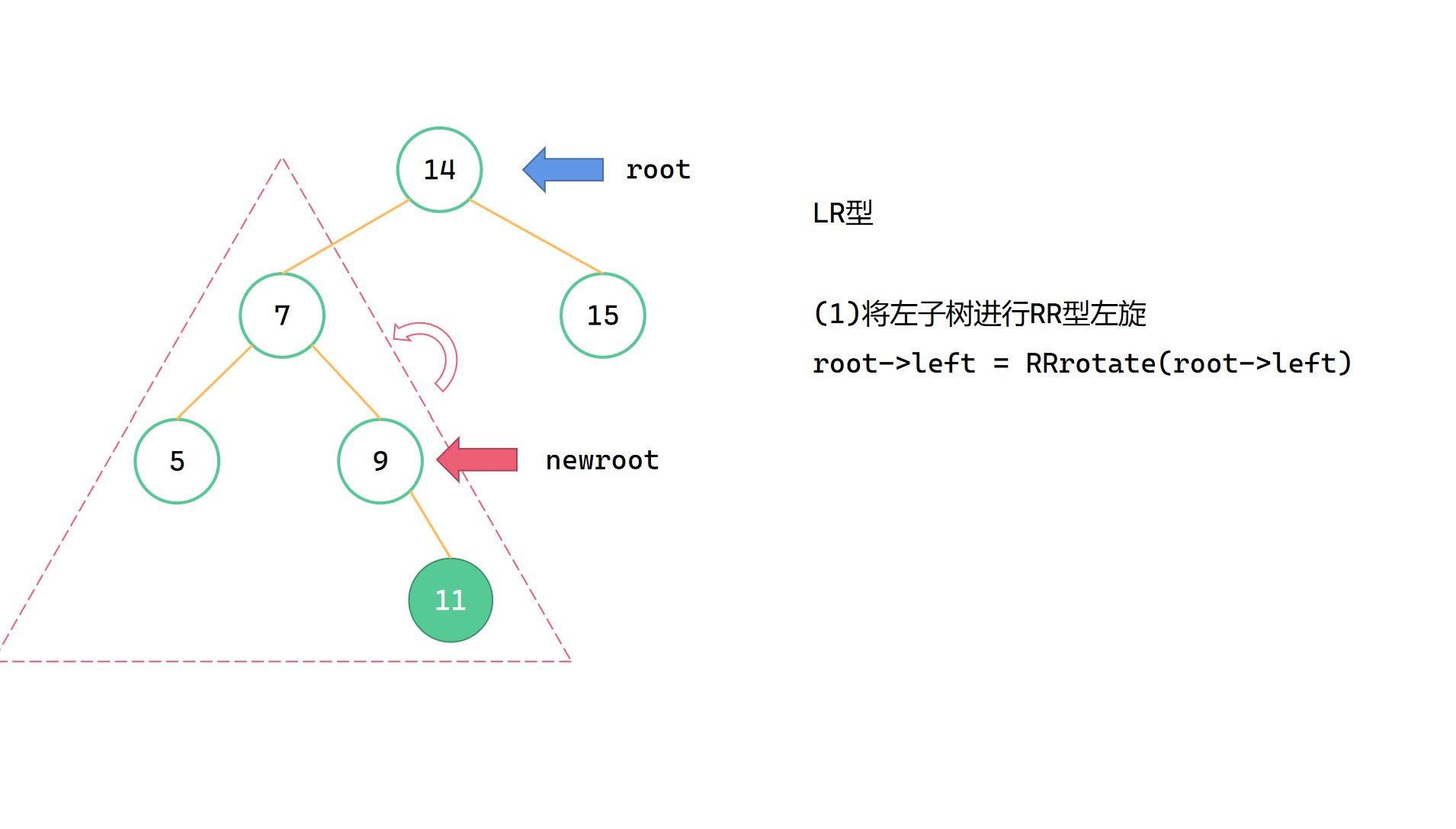
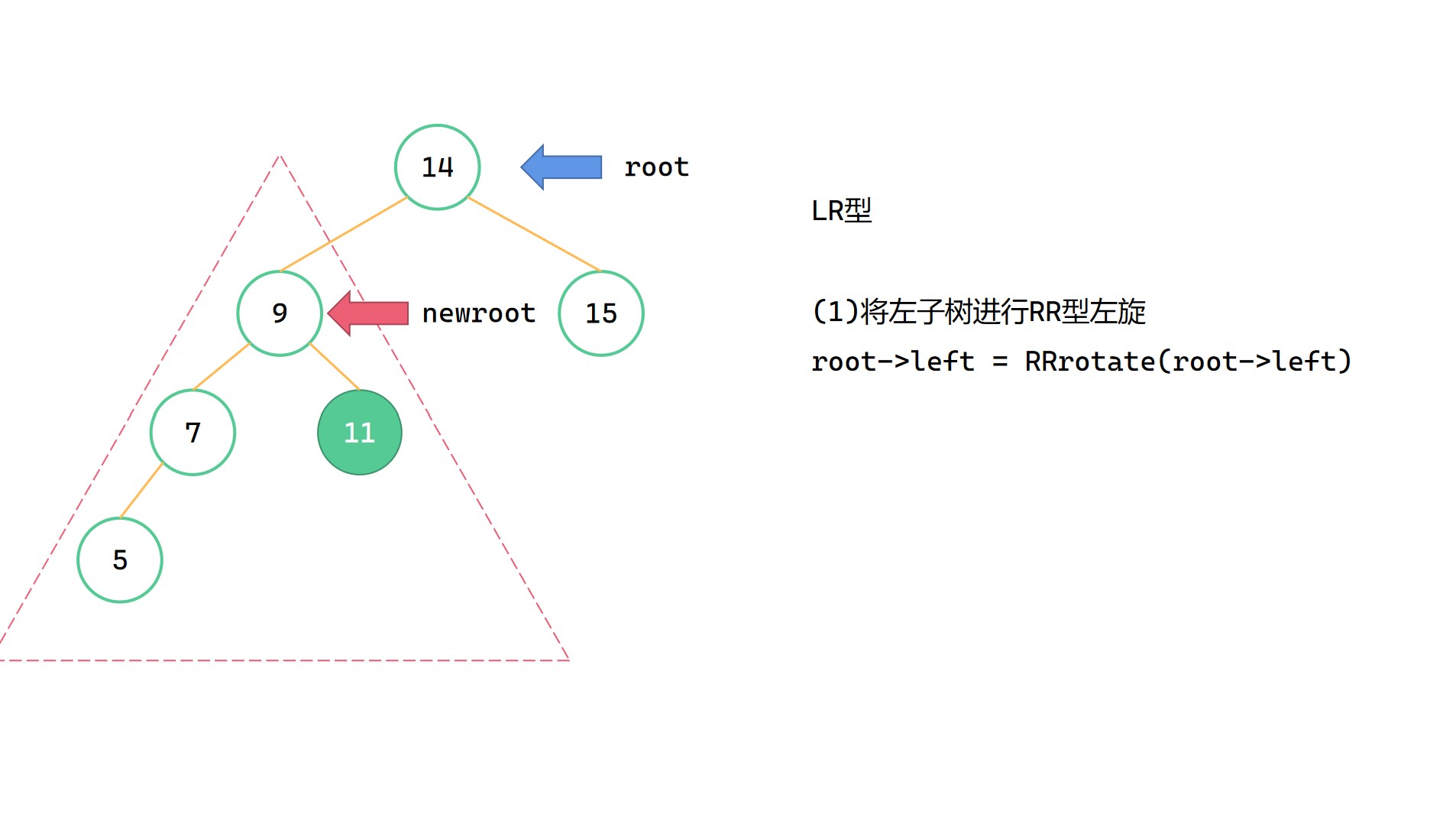
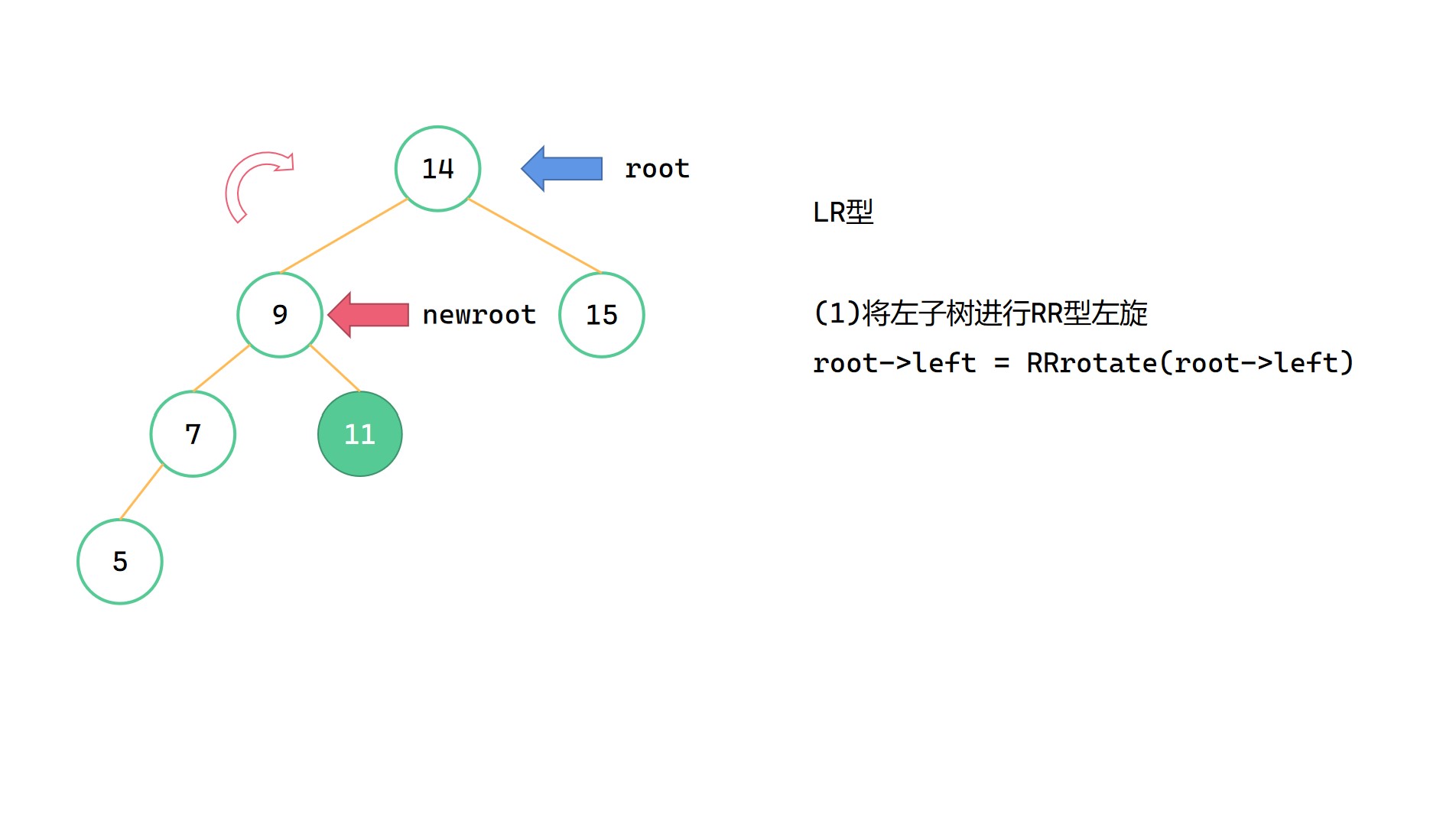
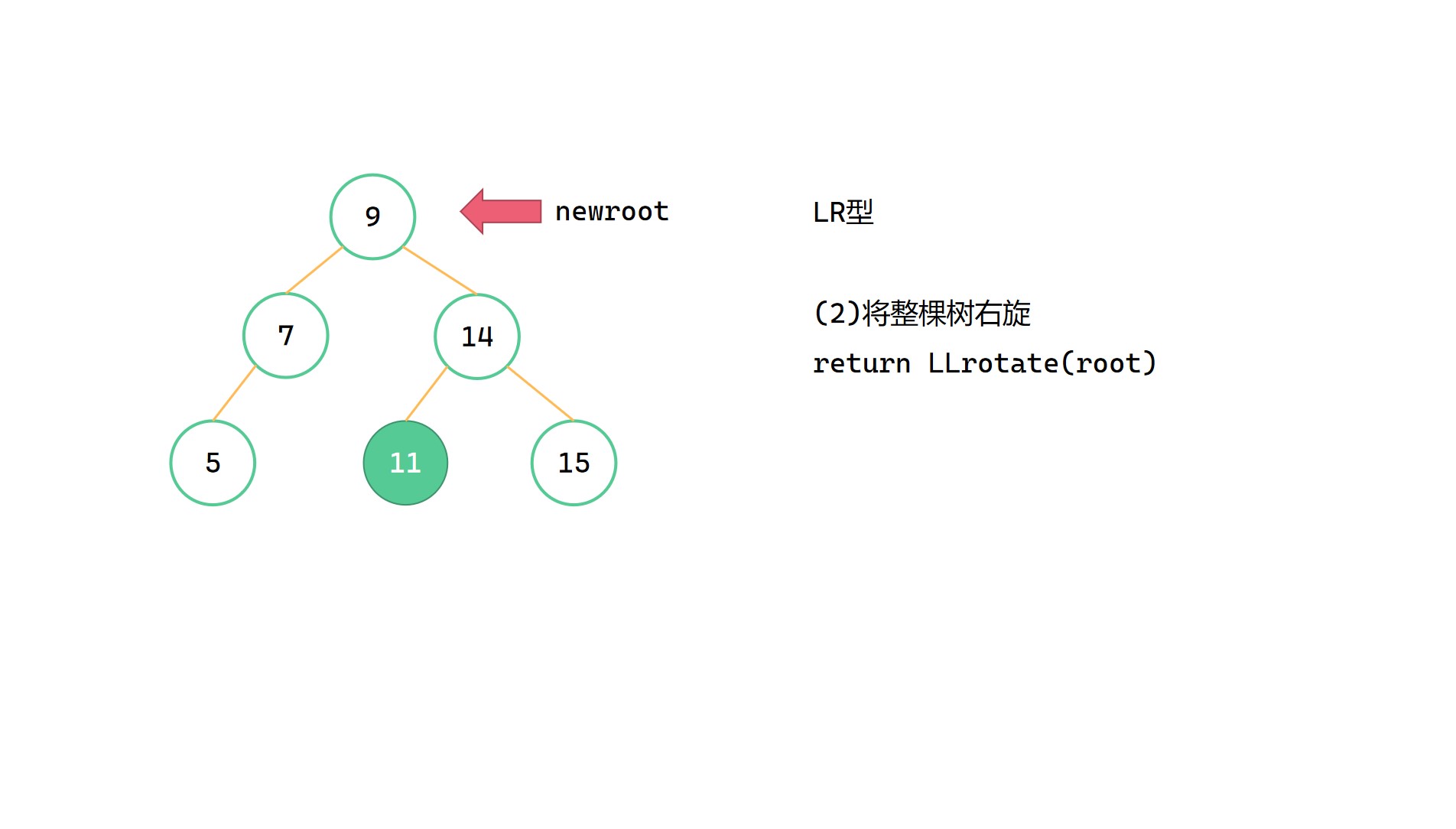
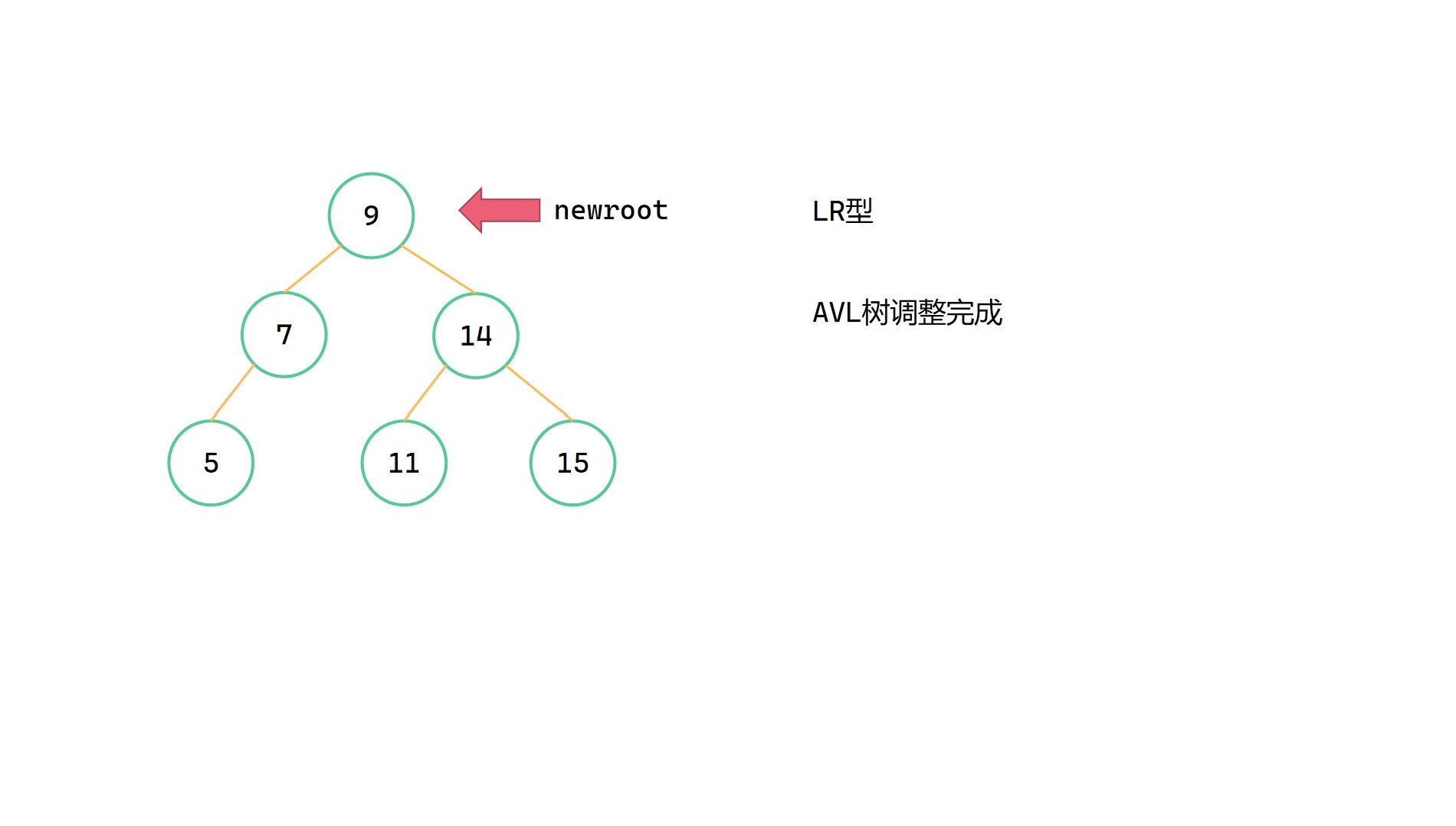
LR型指的是,插入的新节点位于最小不平衡子树根节点 root 的左子树的右子树上,由于左子树过高而导致不平衡。此时我们要先对左子树进行RR型左旋,将整棵树变成LL型的局面,然后对整棵树进行LL右旋。
这类情况看起来要稍微复杂一点,不过之前我们已经实现了LL型和RR型的旋转函数,所以只要建立在这个基础上来实现LR型旋转函数就可以了。
大致步骤为:
(1)root->left = RRrotate(root->left)
(2)return LLrotate(root)
(在RRrotate和LLrotate中已经将高度调整完成了)
LR型旋转 图解
动画演示
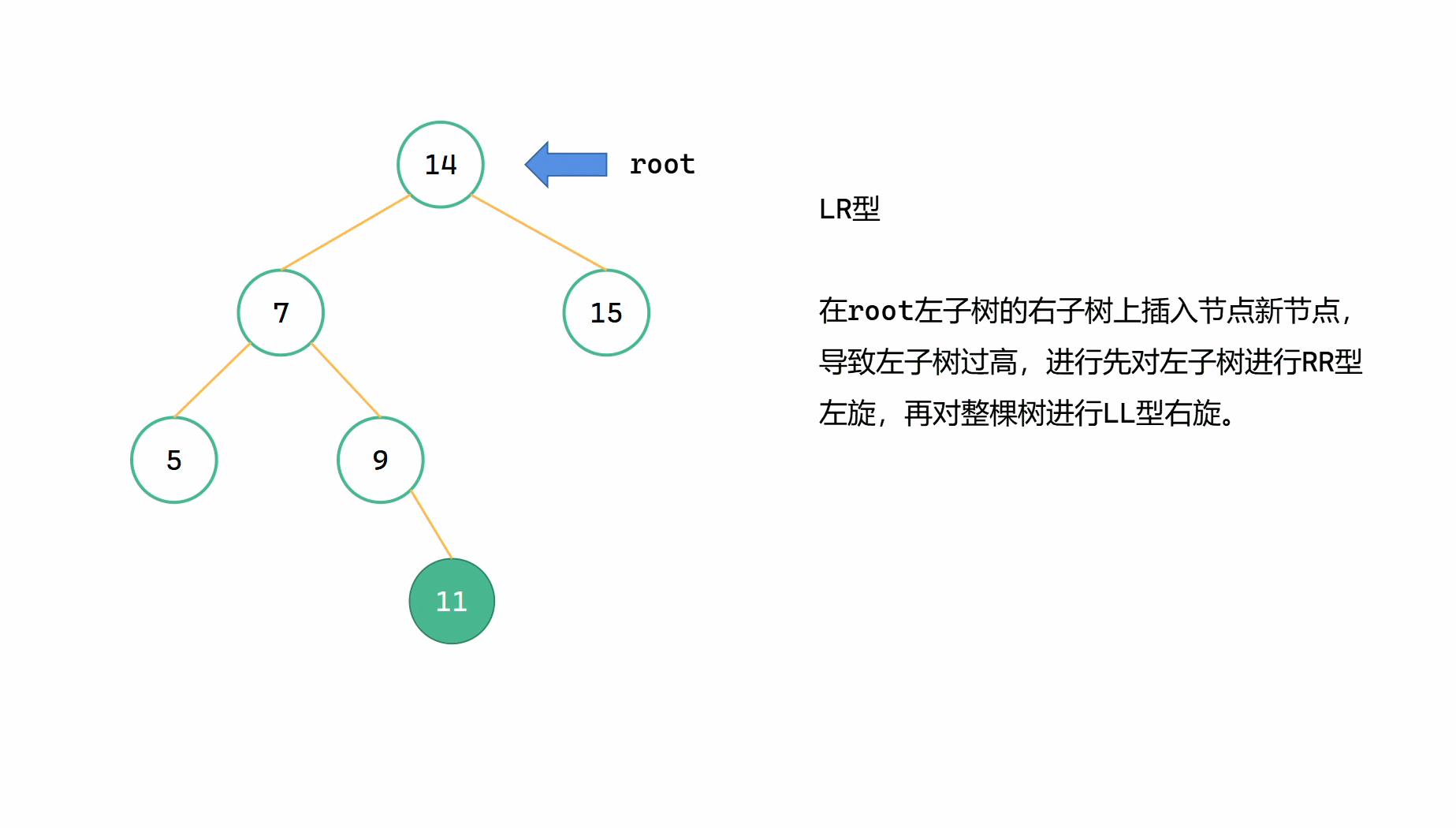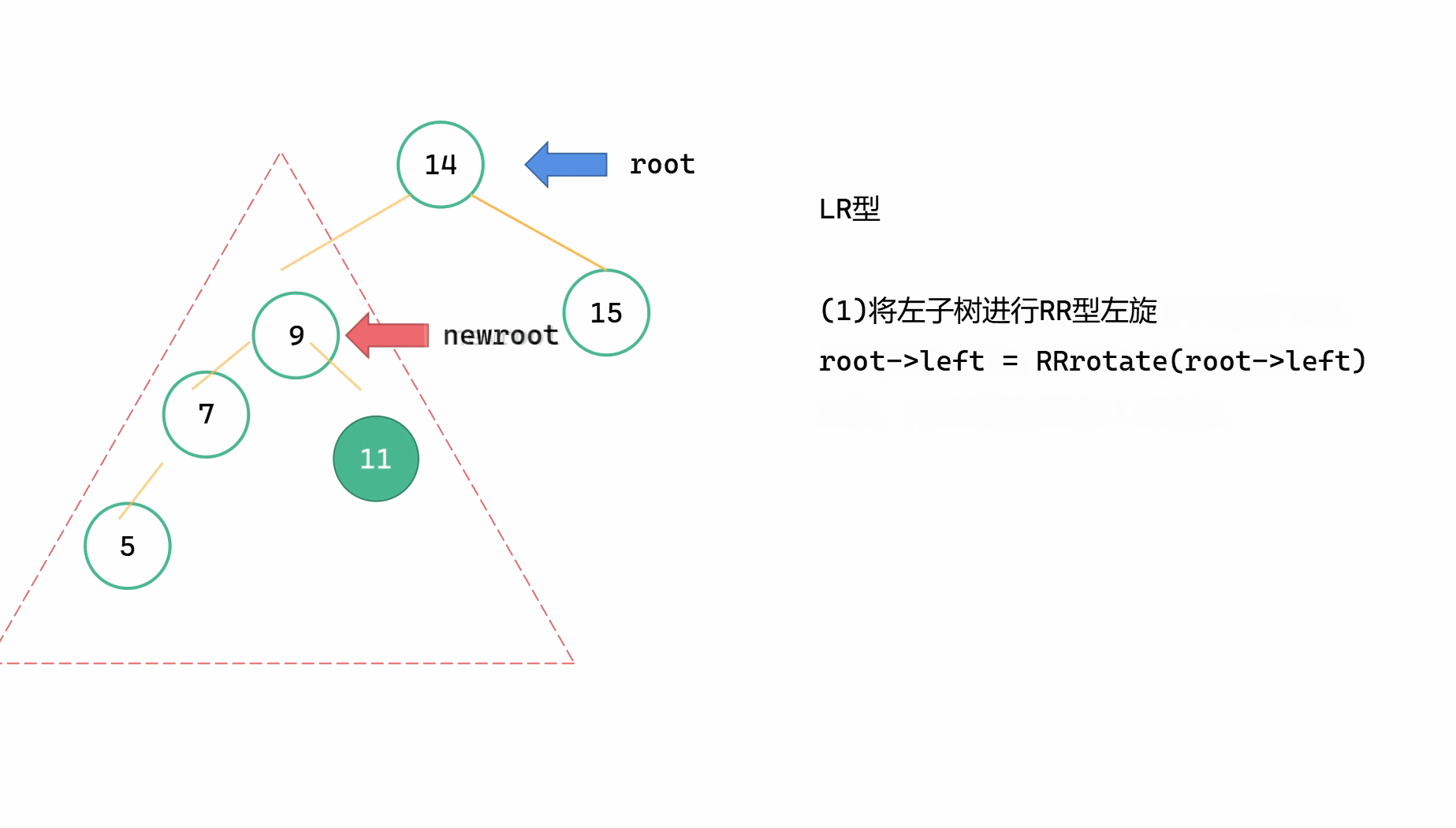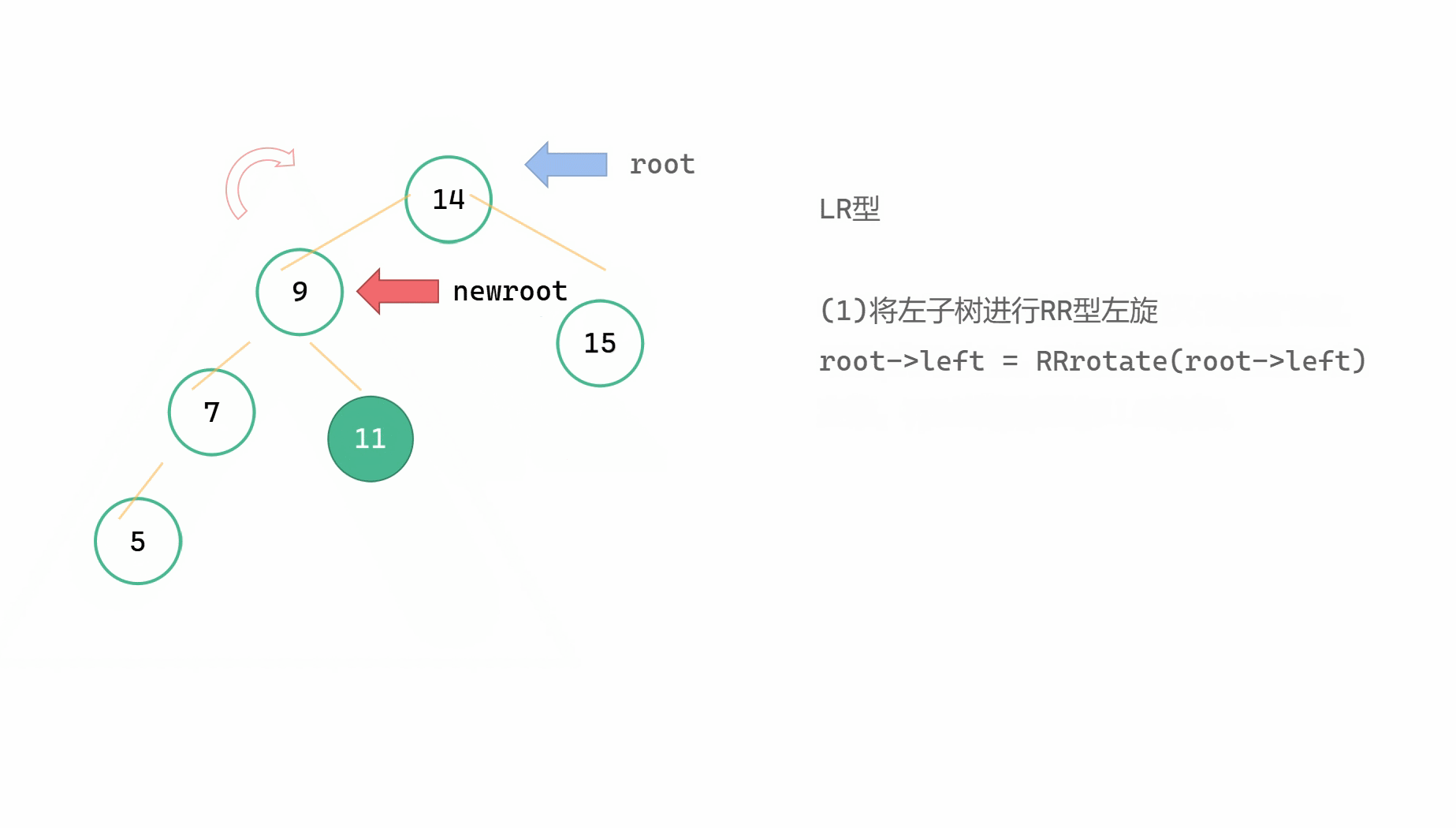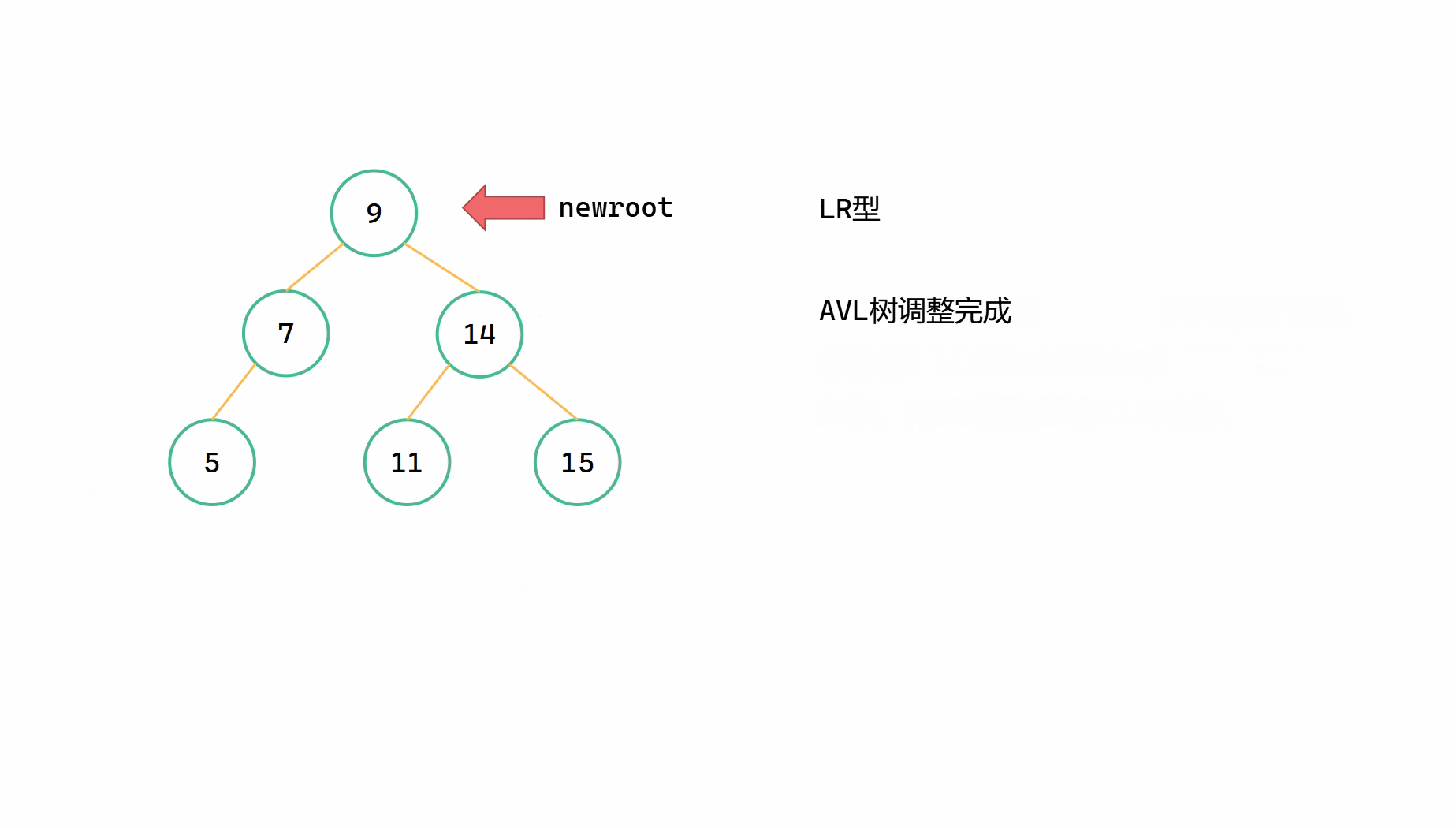
逐帧图解
(1)

(2)
(3)
(4)
(5)
(6)
LR型旋转 代码
//插入节点位于最小不平衡子树根节点root的左儿子的右子树上 LR 先左旋左儿子,再右旋根节点
BinaryTree LR_rotate(BinaryTree &root){
root->left = RR_rotate(root->left); //左旋左儿子
return LL_rotate(root); //右旋根节点
}
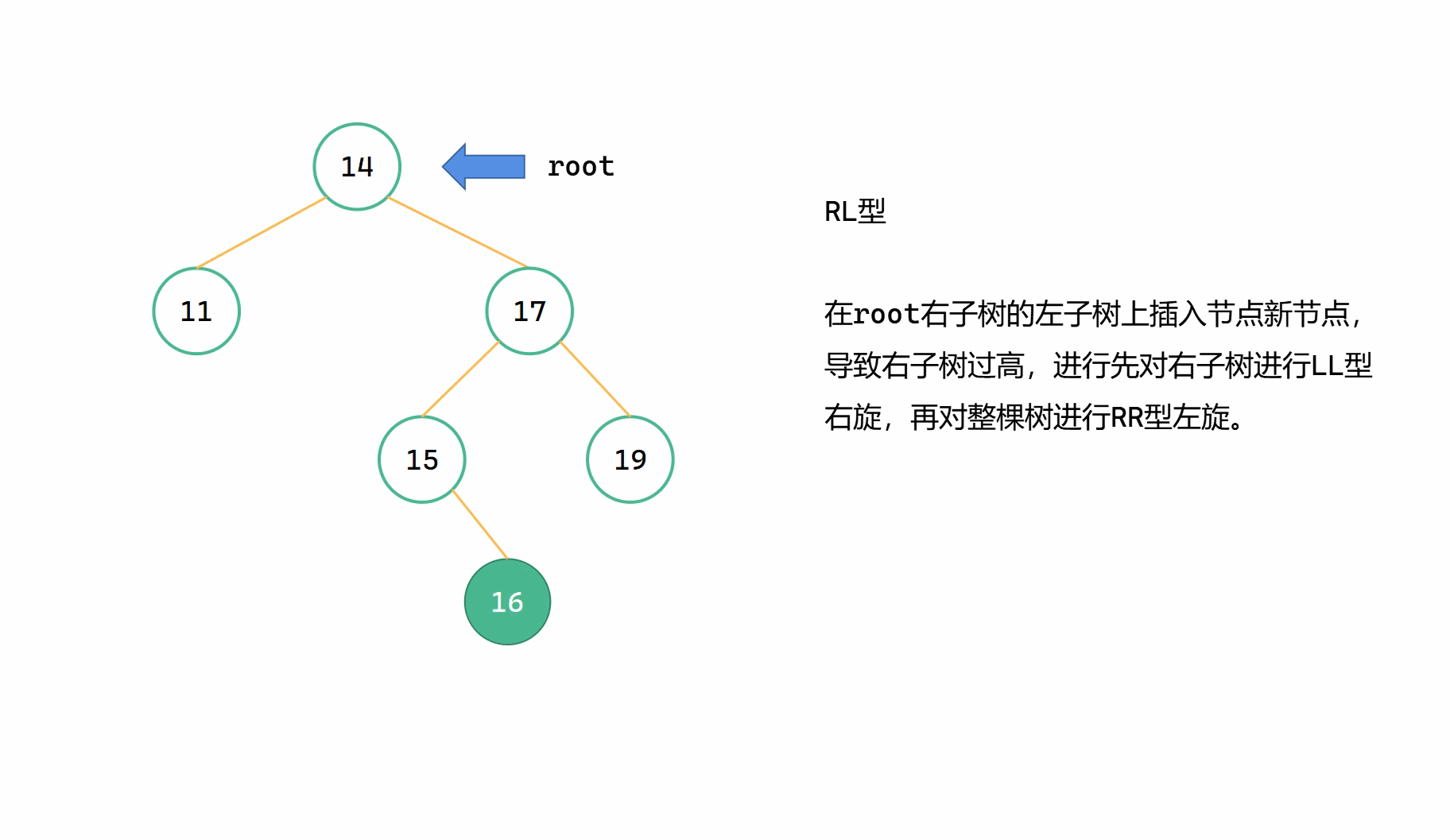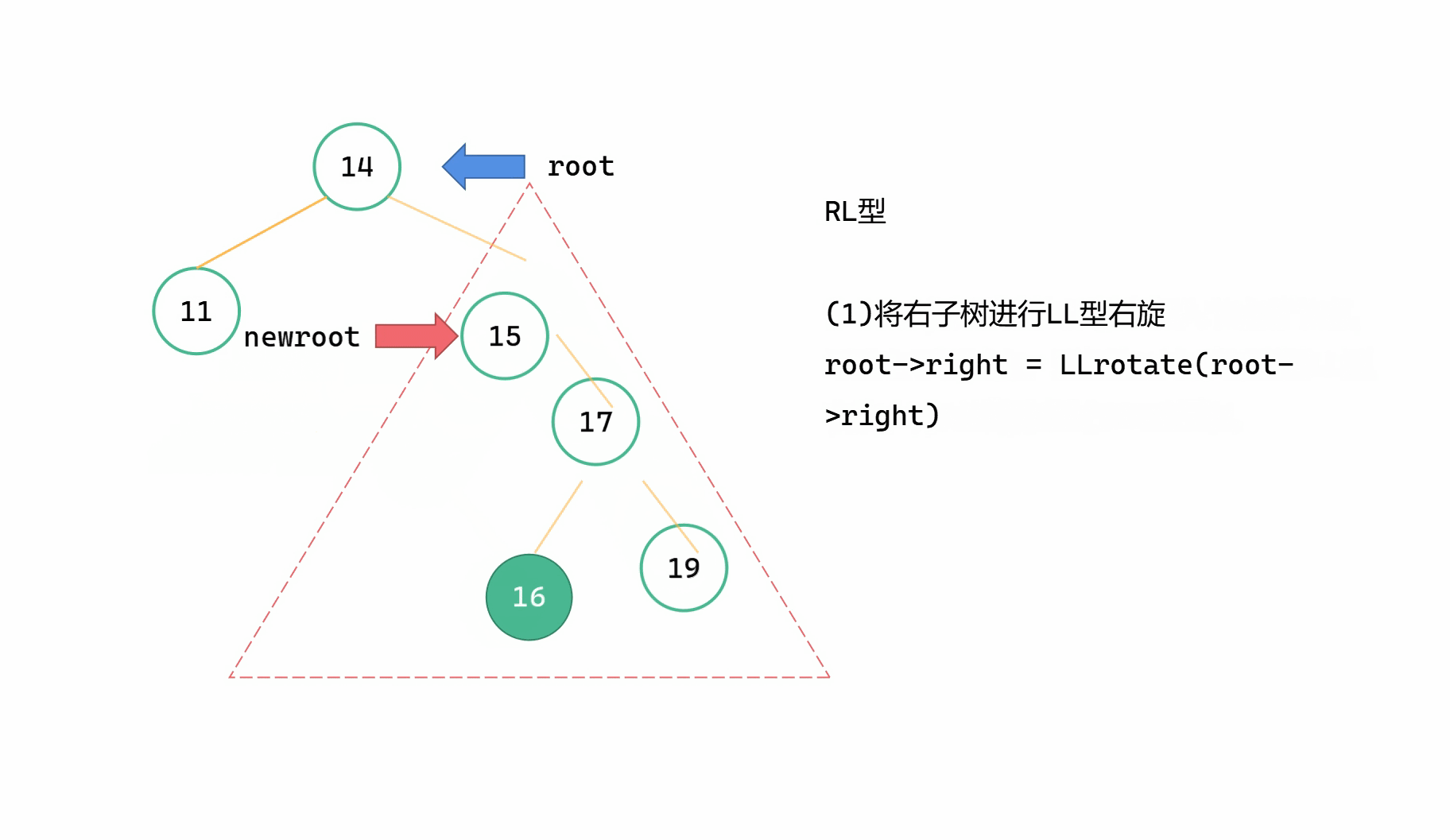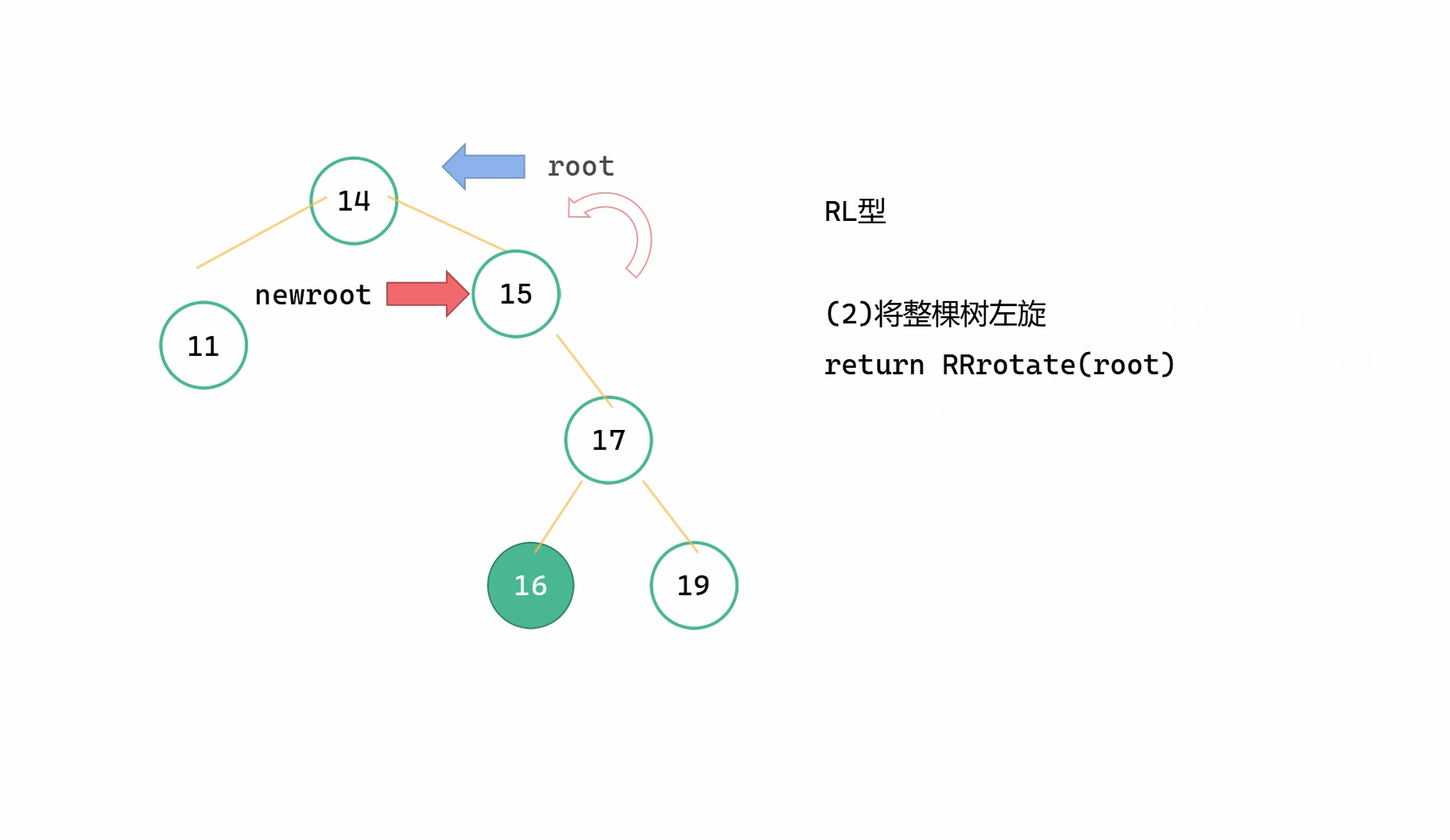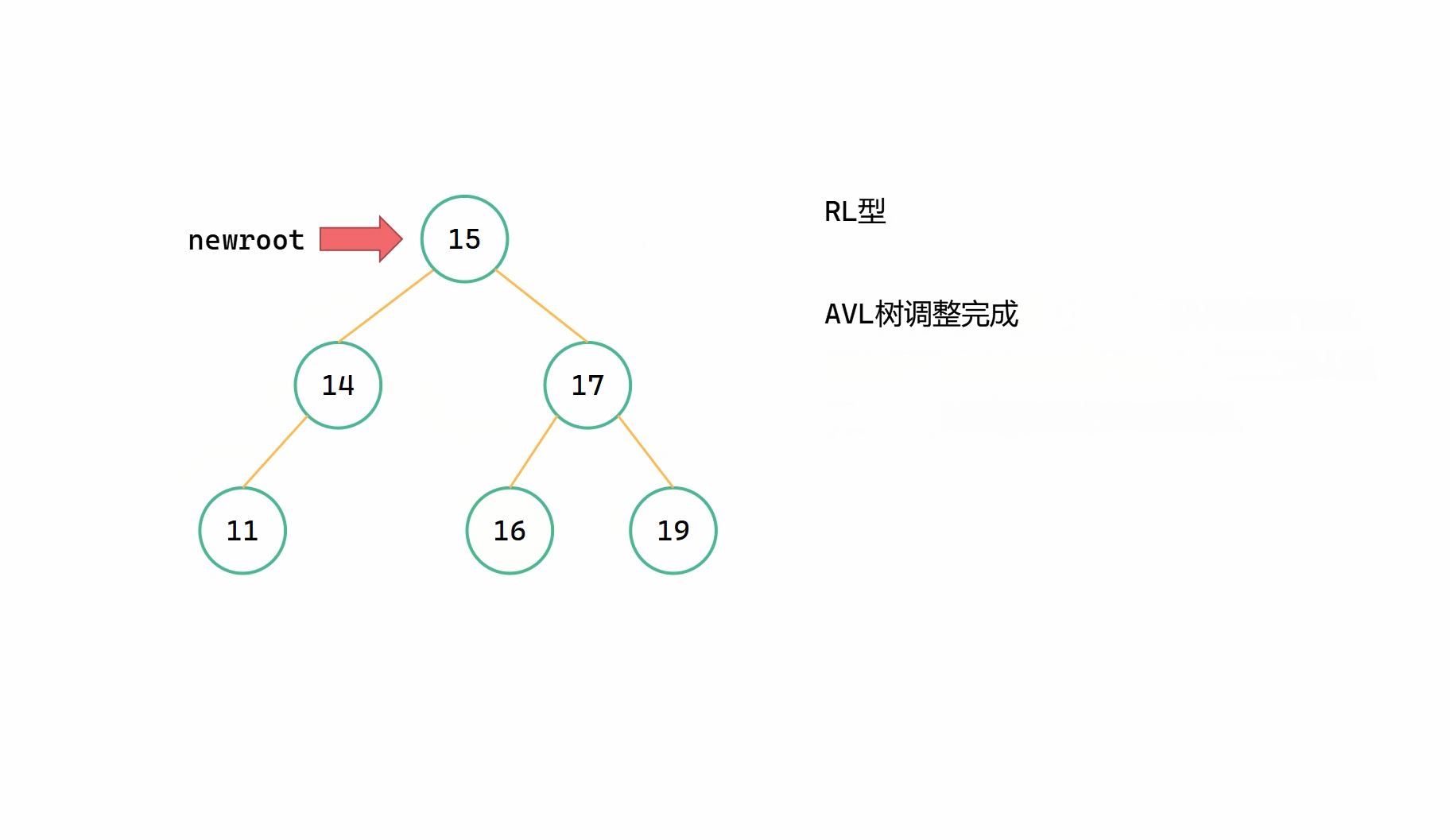
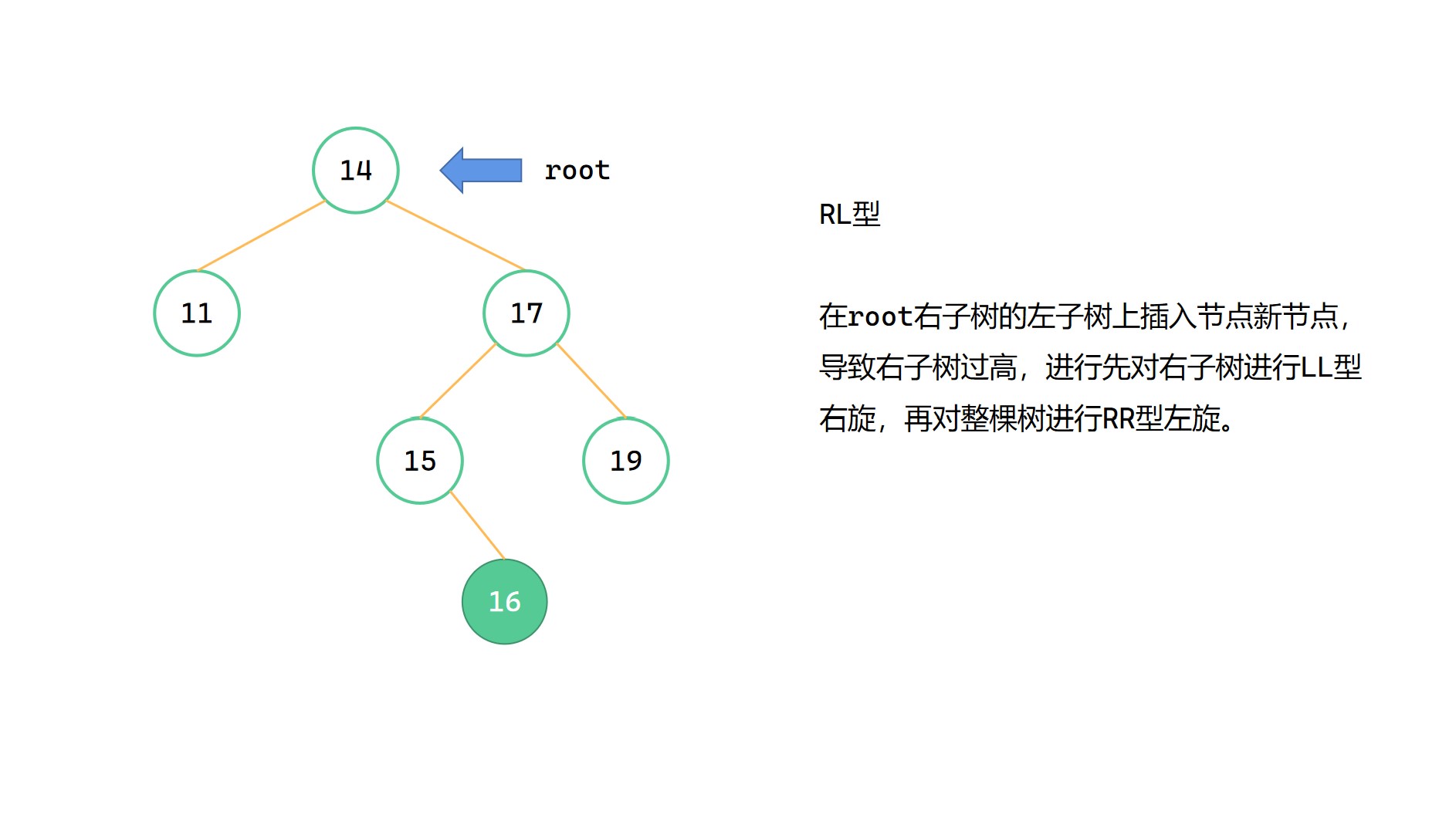
RL型 先右旋再左旋
RL型旋转
RL型指的是,插入的新节点位于最小不平衡子树根节点 root 的右子树的左子树上,由于右子树过高而导致不平衡。此时我们要先对右子树进行LL型右旋,将整棵树变成RR型的局面,然后对整棵树进行RR左旋。
与LR型相类似,只要建立在LL型和RR型的旋转函数的基础上实现就可以。
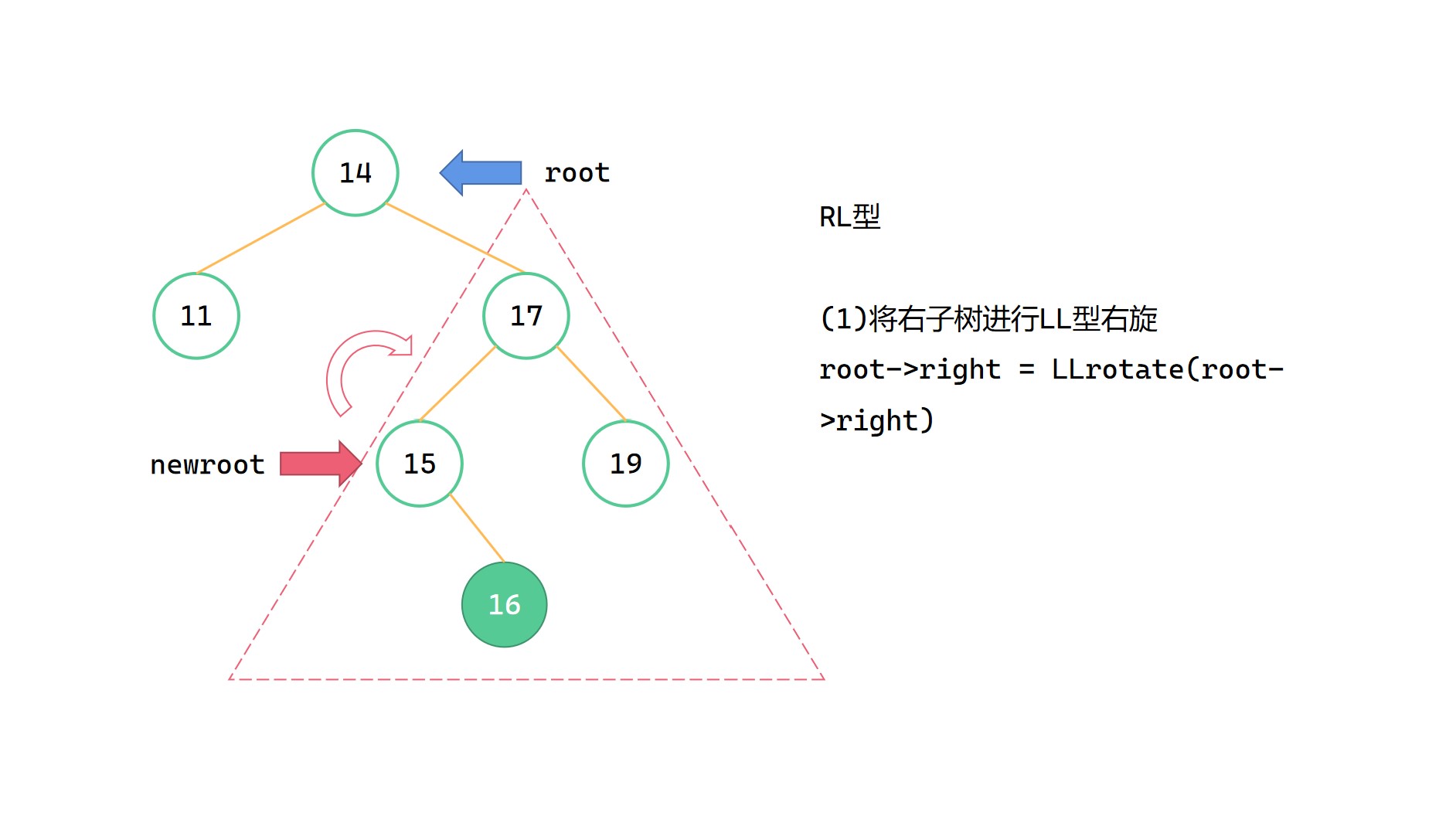
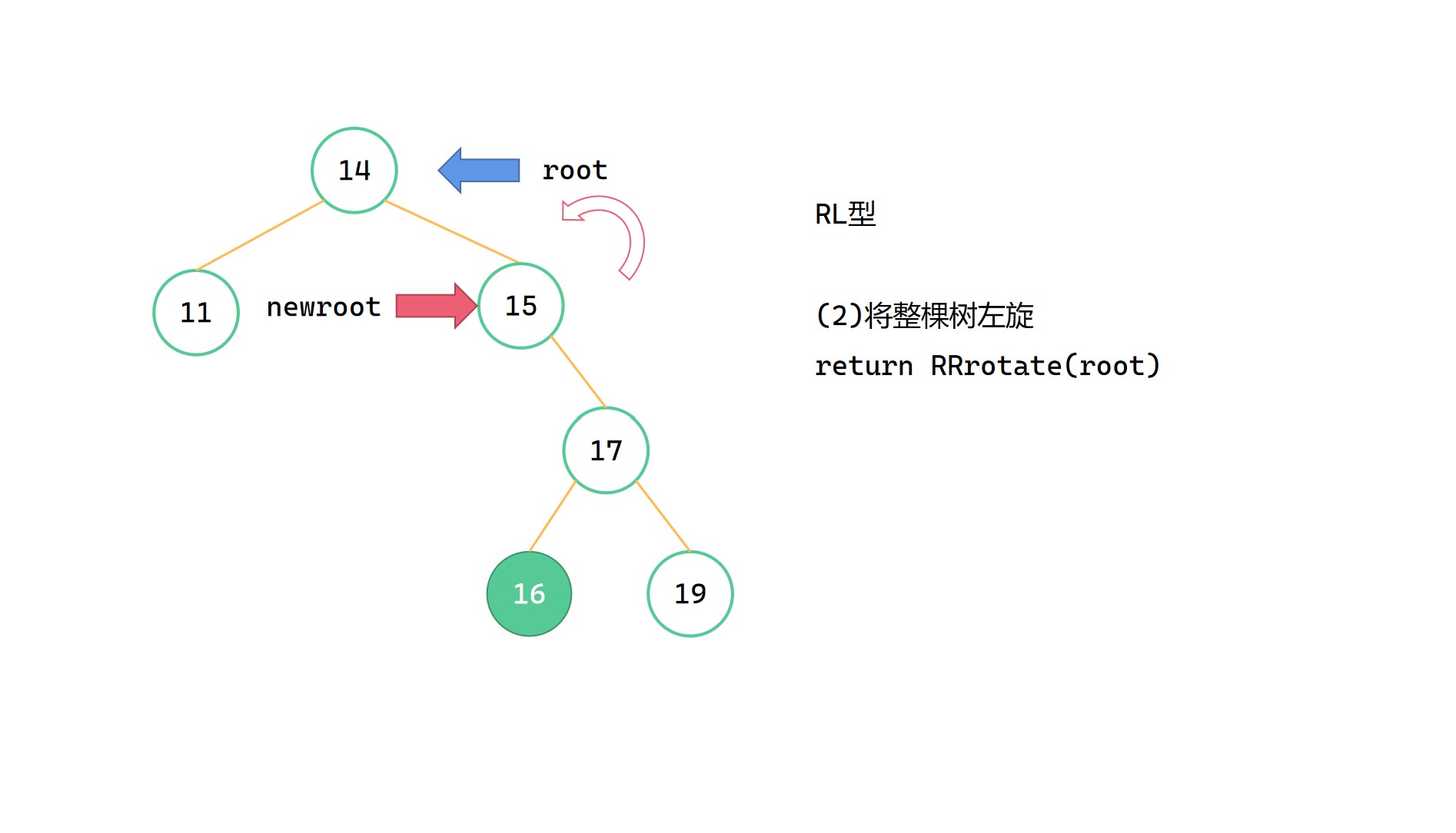
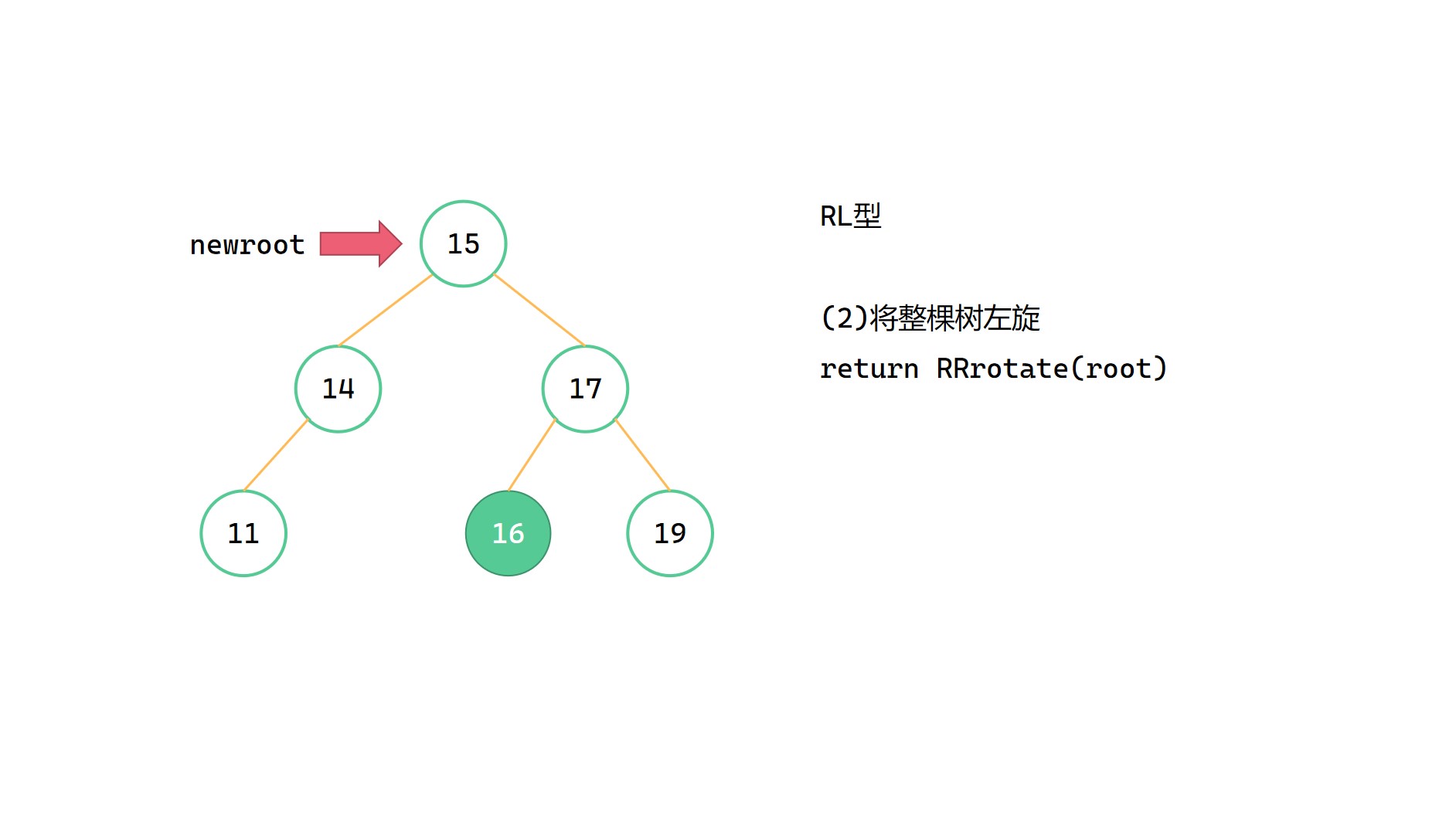
大致步骤为:
(1)root->right = LLrotate(root->right)
(2)return RRrotate(root)
(在LLrotate和RRrotate中已经将高度调整完成了)
RL型旋转 图解
动画演示
逐帧图解
(1)
(2)
(3)

(4)
(5)
(6)

RL型旋转 代码
//插入节点位于最小不平衡子树根节点root的右儿子的左子树上 RL 先右旋右儿子,再左旋根节点
BinaryTree RL_rotate(BinaryTree &root){
root->right = LL_rotate(root->right);//右旋右儿子
return RR_rotate(root); //左旋根节点
}
AVL树插入时旋转方式的判断
插入后左子树更高且高度差大于1
(1)插入节点值比左子树根节点值小:此时插入节点位于左子树的左子树上,为 LL型
(2)插入节点值比左子树根节点值大:此时插入节点位于左子树的右子树上,为 LR型
插入后右子树更高且高度差大于1
(1)插入节点值比右子树根节点值大:此时插入节点位于右子树的右子树上,为 RR型
(2)插入节点值比右子树根节点值小:此时插入节点位于右子树的左子树上,为 RL型
AVL树插入操作代码
//AVL树的插入
void Insert_AVL(BinaryTree &root, int val){
BinaryTree node = (BinaryTree)malloc(sizeof(BiNode));
node->val = val;
node->left = node->right = NULL;
node->height = 1; //高度初始为1
if(!root){
root = node;
return;
}
if(root->val == val)
return; //已经存在这个值的节点 则不插入
//递归插入AVL树
if(root->val > val){ //向左子树插入,有可能会使左子树变高
Insert_AVL(root->left, val);
//插入之后不平衡的调整
if(GetHeight(root->left) - GetHeight(root->right) > 1){
if(root->left->val > val){
root = LL_rotate(root); //如果插入位置为左儿子的左子树LL,右旋
}else{
root = LR_rotate(root); //如果插入位置为左儿子的右子树LR,先左旋再右旋
}
}
}else{ //向右子树插入 有可能会使右子树变高
Insert_AVL(root->right, val);
//插入后不平衡的调整
if(GetHeight(root->right) - GetHeight(root->left) > 1){
if(root->right->val < val){
root = RR_rotate(root); //如果插入位置为右儿子的右子树RR,左旋
}else{
root = RL_rotate(root); //如果插入位置为右儿子的左子树RL,先右旋再左旋
}
}
}
//更新高度
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
}
AVL树的删除操作时的调整
AVL树删除操作部分和二叉搜索树是一样的,其中删除节点存在左右子树这一块比较复杂,如果有困惑的可以看我之前的一篇有关二叉搜索树的博客:
[数据结构] 二叉搜索树 (二叉排序树)
AVL树删除时旋转方式的判断
删除后左子树更高且高度差大于1
(1)左子树的左子树比左子树的右子树高:删除后形成了 LL型 的局面
(2)左子树的右子树比左子树的左子树高:删除后形成了 LR型 的局面
删除后右子树更高且高度差大于1
(1)右子树的右子树比右子树的左子树高:删除后形成了 RR型 的局面
(2)右子树的左子树比右子树的右子树高:删除后形成了 RL型 的局面
AVL树删除操作代码
//AVL删除节点
BinaryTree Delete_AVL(BinaryTree &root, int val){
BinaryTree t = root, parent = NULL, s = NULL;
if(!t){
puts("要删除的节点不存在");
return root;
}
/* 删除操作 */
if(t->val > val){
root->left = Delete_AVL(root->left, val); //对左子树进行删除节点
}else if(t->val < val){
root->right = Delete_AVL(root->right, val); //对右子树进行删除节点
}else{
//当前root为删除的节点
//判断此子树的性质
if(!t->left && !t->right){ //**如果此子树没有儿子
root = NULL; // 直接删除即可
}else if(!t->left && t->right){ //**如果没有左儿子 但是有右儿子
root = t->right; // 将其右儿子代替当前删除的节点即可
}else if(t->left && !t->right){ //**如果有左儿子 但是没有右儿子
root = t->left; // 将其左儿子代替当前删除的节点即可
}else{ //**如果既有右儿子又有左儿子 就比较麻烦了
s = t->right; // 记录删除节点的右子树根节点
if(!s->left){
s->left = t->left; //如果删除节点的右子树没有左儿子 只要将删除节点的左子树继承给s即可
}else{
//需找到删除节点右子树中最左边的节点 即第一个大于删除节点值的节点
while(s->left){
parent = s; //记录s的父节点
s = s->left;
}
parent->left = s->right; //若第一个大于删除节点的节点有右子树 继承给其父节点作为其左子树
s->left = t->left; //代替删除节点 继承其左子树
s->right = t->right; //代替删除节点 继承其右子树
}
root = s; //更新子树根
}
free(t);
}
/* 平衡操作 */
if(!root)
return NULL; //上面递归完之后若根节点都被删了
//删除操作后可能需要调整高度
if(GetHeight(root->left) - GetHeight(root->right) > 1){
//左子树比右子树高 说明删除了右子树中的节点
//变向地认为在左子树中插入了节点 需要进行右旋
if(GetHeight(root->left->left) > GetHeight(root->left->right)){
return LL_rotate(root); //左子树的左边更高 需要进行 LL 的右旋
}else{
return LR_rotate(root); //左子树的右边高 需要进行 LR 的右旋
}
}else if(GetHeight(root->right) - GetHeight(root->left) > 1){
//右子树比左子树更高 说明删除的是左子树中的节点
//变向地认为在右子树插入了节点 需要进行左旋
if(GetHeight(root->right->right) > GetHeight(root->right->left)){
return RR_rotate(root); //右子树的右边更高 需要进行 RR 的左旋
}else{
return RL_rotate(root); //右子树的左边更高 需要进行 RL 的左旋
}
}
//更新root的高度
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
return root;
}
程序测试
完整程序代码
点击查看代码☺☺☺
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<vector>
#include<algorithm>
#include<queue>
//AVL树 Adelson-Velskii Landis
typedef struct BiNode{
int val;
int height; //需记录每个节点的高度
struct BiNode *left, *right;
}BiNode, *BinaryTree;
//判断是否存在target值节点
BinaryTree Search_AVL(BinaryTree root, int target){
if(!root) return NULL;
if(target == root->val) return root;
if(target > root->val)
return Search_AVL(root->left, target);
else
return Search_AVL(root->right, target);
}
//返回节点的高度
int GetHeight(BinaryTree root){
return root ? root->height : 0;
}
//插入节点位于最小不平衡子树根节点的左儿子的左子树上 LL 进行右旋
BinaryTree LL_rotate(BinaryTree &root){
BinaryTree newroot = root->left; //右旋,左儿子成为新的根节点
root->left = newroot->right; //左儿子的右子树成为根节点的左子树
newroot->right = root; //之前根节点成为新根节点的右子树
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
newroot->height = std::max(GetHeight(newroot->left), GetHeight(newroot->right)) + 1;
return newroot;
}
//插入节点位于最小不平衡子树根节点的右儿子的右子树上 RR 进行左旋
BinaryTree RR_rotate(BinaryTree &root){
BinaryTree newroot = root->right; //左旋,右儿子变成新的根节点
root->right = newroot->left; //右儿子的左子树变成当前根节点的右子树
newroot->left = root; //原先根节点变成新根节点的左子树
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
newroot->height = std::max(GetHeight(newroot->left), GetHeight(newroot->right)) + 1;
return newroot;
}
//插入节点位于最小不平衡子树根节点root的左儿子的右子树上 LR 先左旋左儿子,再右旋根节点
BinaryTree LR_rotate(BinaryTree &root){
root->left = RR_rotate(root->left); //左旋左儿子
return LL_rotate(root); //右旋根节点
}
//插入节点位于最小不平衡子树根节点root的右儿子的左子树上 RL 先右旋右儿子,再左旋根节点
BinaryTree RL_rotate(BinaryTree &root){
root->right = LL_rotate(root->right);//右旋右儿子
return RR_rotate(root); //左旋根节点
}
//AVL树的插入
void Insert_AVL(BinaryTree &root, int val){
BinaryTree node = (BinaryTree)malloc(sizeof(BiNode));
node->val = val;
node->left = node->right = NULL;
node->height = 1;
if(!root){
root = node;
return;
}
if(root->val == val)
return; //已经存在这个值的节点 则不插入
//递归插入AVL树
if(root->val > val){ //向左子树插入,有可能会使左子树变高
Insert_AVL(root->left, val);
//插入之后不平衡的调整
if(GetHeight(root->left) - GetHeight(root->right) > 1){
if(root->left->val > val){
root = LL_rotate(root); //如果插入位置为左儿子的左子树LL,右旋
}else{
root = LR_rotate(root); //如果插入位置为左儿子的右子树LR,先左旋再右旋
}
}
}else{ //向右子树插入 有可能会使右子树变高
Insert_AVL(root->right, val);
//插入后不平衡的调整
if(GetHeight(root->right) - GetHeight(root->left) > 1){
if(root->right->val < val){
root = RR_rotate(root); //如果插入位置为右儿子的右子树RR,左旋
}else{
root = RL_rotate(root); //如果插入位置为右儿子的左子树RL,先右旋再左旋
}
}
}
//更新高度
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
}
//构建AVL树
void Create_AVL(BinaryTree &root, std::vector<int> &v){
for(auto x : v) Insert_AVL(root, x);
}
//AVL删除节点
BinaryTree Delete_AVL(BinaryTree &root, int val){
BinaryTree t = root, parent = NULL, s = NULL;
if(!t){
puts("要删除的节点不存在");
return root;
}
/* 删除操作 */
if(t->val > val){
root->left = Delete_AVL(root->left, val); //对左子树进行删除节点
}else if(t->val < val){
root->right = Delete_AVL(root->right, val); //对右子树进行删除节点
}else{
//当前root为删除的节点
//判断此子树的性质
if(!t->left && !t->right){ //**如果此子树没有儿子
root = NULL; // 直接删除即可
}else if(!t->left && t->right){ //**如果没有左儿子 但是有右儿子
root = t->right; // 将其右儿子代替当前删除的节点即可
}else if(t->left && !t->right){ //**如果有左儿子 但是没有右儿子
root = t->left; // 将其左儿子代替当前删除的节点即可
}else{ //**如果既有右儿子又有左儿子 就比较麻烦了
s = t->right; // 记录删除节点的右子树根节点
if(!s->left){
s->left = t->left; //如果删除节点的右子树没有左儿子 只要将删除节点的左子树继承给s即可
}else{
//需找到删除节点右子树中最左边的节点 即第一个大于删除节点值的节点
while(s->left){
parent = s; //记录s的父节点
s = s->left;
}
parent->left = s->right; //若第一个大于删除节点的节点有右子树 继承给其父节点作为其左子树
s->left = t->left; //代替删除节点 继承其左子树
s->right = t->right; //代替删除节点 继承其右子树
}
root = s; //更新子树根
}
free(t);
}
/* 平衡操作 */
if(!root)
return NULL; //上面递归完之后若根节点都被删了
//删除操作后可能需要调整高度
if(GetHeight(root->left) - GetHeight(root->right) > 1){
//左子树比右子树高 说明删除了右子树中的节点
//变向地认为在左子树中插入了节点 需要进行右旋
if(GetHeight(root->left->left) > GetHeight(root->left->right)){
return LL_rotate(root); //左子树的左边更高 需要进行 LL 的右旋
}else{
return LR_rotate(root); //左子树的右边高 需要进行 LR 的右旋
}
}else if(GetHeight(root->right) - GetHeight(root->left) > 1){
//右子树比左子树更高 说明删除的是左子树中的节点
//变向地认为在右子树插入了节点 需要进行左旋
if(GetHeight(root->right->right) > GetHeight(root->right->left)){
return RR_rotate(root); //右子树的右边更高 需要进行 RR 的左旋
}else{
return RL_rotate(root); //右子树的左边更高 需要进行 RL 的左旋
}
}
// 更新root的高度
root->height = std::max(GetHeight(root->left), GetHeight(root->right)) + 1;
return root;
}
//中序遍历
void ShowInfixOrder(BinaryTree root){
if(!root)
return;
ShowInfixOrder(root->left);
printf("%d ", root->val);
ShowInfixOrder(root->right);
}
//层次遍历
void ShowLevelOrder(BinaryTree root){
if(!root)
return;
std::queue<BinaryTree> q;
q.push(root);
while(!q.empty()){
int n = q.size();
for(int i = 0; i < n; i++){
BinaryTree t = q.front();
q.pop();
printf("%d ", t->val);
if(t->left)
q.push(t->left);
if(t->right)
q.push(t->right);
}
printf("\n");
}
}
int main(){
BinaryTree T = NULL;
std::vector<int> v = {12, 9, 18, 16, 20, 15};
Create_AVL(T, v);
printf("AVL树中序遍历和层次遍历:\n");
ShowInfixOrder(T);
printf("\n\n");
ShowLevelOrder(T);
printf("\n删除值为9节点的AVL树:\n");
T = Delete_AVL(T, 9);
ShowInfixOrder(T);
printf("\n\n");
ShowLevelOrder(T);
}
程序测试结果

一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MAKISE004/p/17114705.html,未经允许严禁转载


