Lecture 07 Functional Dependency

First Normal Form：

Domain is atomic if its elements are considered to be indivisible units

A relational schema R is in first normal form if the domains of all attributes of R are atomic

 

Design Goals:

Avoid redundant data
Ensure that relationships among attributes are represented

Facilitate the checking of updates for violation database integrity constraints.

 

Higher Normal forms — Devise a Theory for the Following： 

Decide whether a particular relation R is in “good” form.
In the case that a relation R is not in “good” form, decompose it into a

set of relations {R1, R2, ..., Rn} such that

each relation is in good form

the decomposition is a lossless-join decomposition

Our theory is based on:

functional dependencies
multivalued dependencies [skipping]

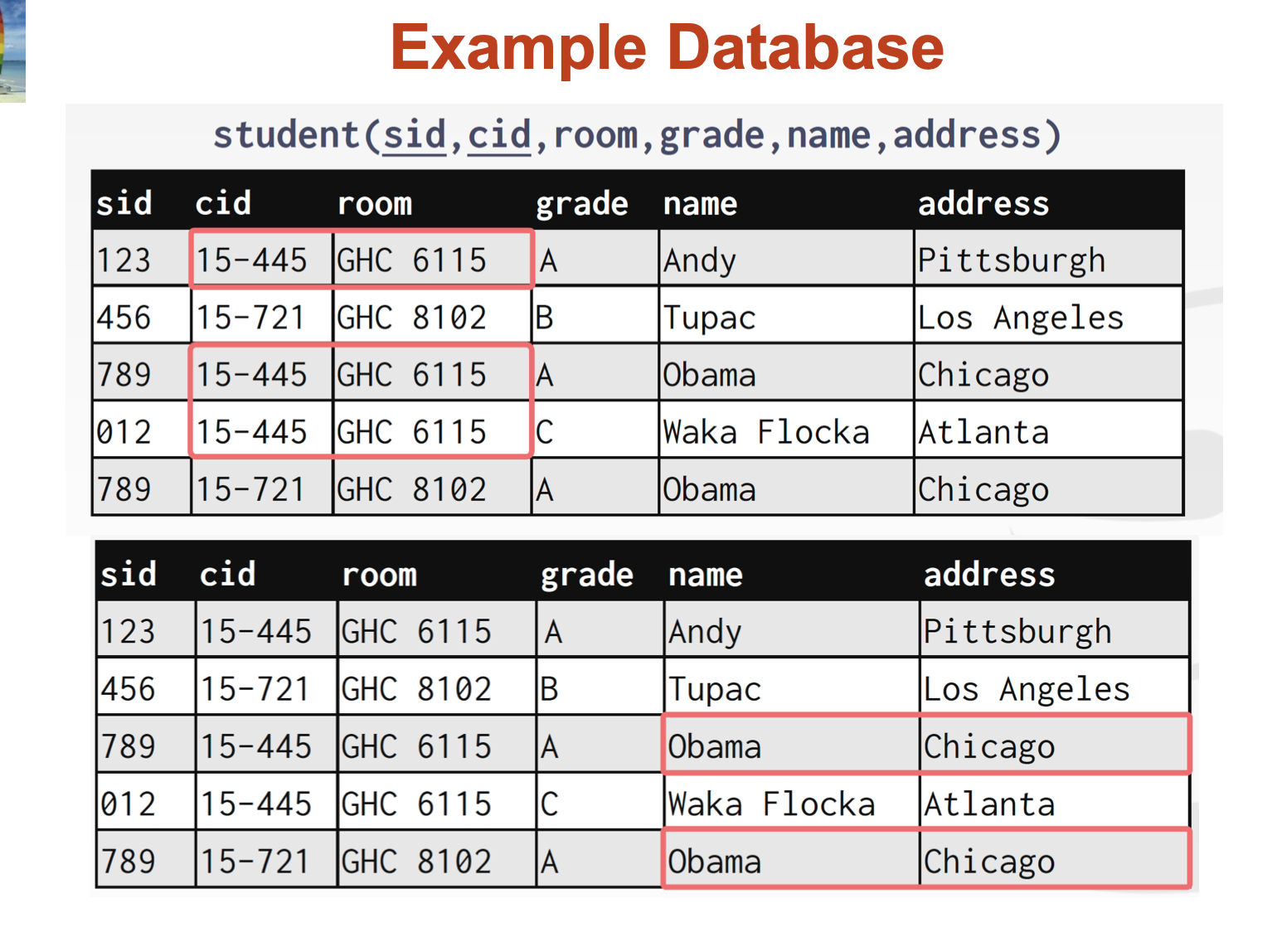
Update Anomalies：

Redundancy Problems

If the room number changes, we need to make sure that we change all students records

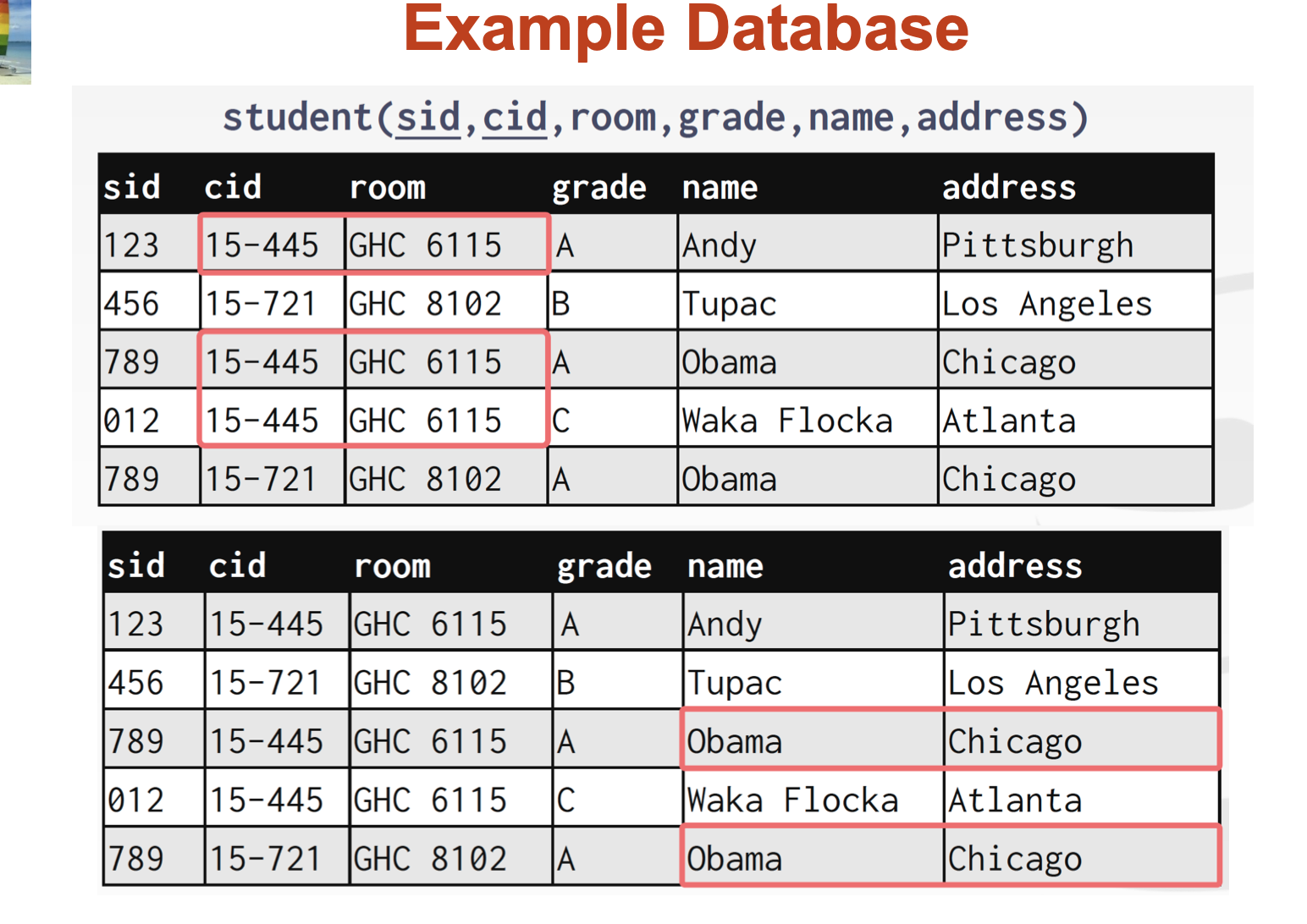
Insert Anomalies

May not be possible to add a student unless they’re enrolled in a course

Delete Anomalies

If all the students enrolled in a course are deleted, then we lose the room number

Functional Dependencies:

A Functional Dependency (FD) is a form of a constraint. Part of a relation’s schema to define a valid instance.

Use of Functional Dependencies：

We use functional dependencies to:

1.test relations to see if they are legal under a given set of functional dependencies.

 If a relation r is legal under a set F of functional dependencies, we say that r satisfies F.

2.specify constraints on the set of legal relations

 We say that F holds on R if all legal relations on R satisfy the set of functional dependencies F.

 

Closure of a Set of Functional Dependencies：

Given a set F set of functional dependencies, there are certain other functional dependencies that are logically implied by F.

For e.g.: If AB and BC, then we can infer that AC

The set of all func. dependencies logically implied by F is the closure of F.

We denote the closure of F by F+.

We can find F+, the closure of F, by repeatedly applying Armstrong’s Axioms:

 

 

Example：

 

 

We want a minimal set of FDs that was enough to ensure correctness.

Maintaining the closure at runtime is expensive.

It allows us to find the super key for a relation.

 

Recall of Relational Model:

Decomposition Goals:

Lossless Decomposition:

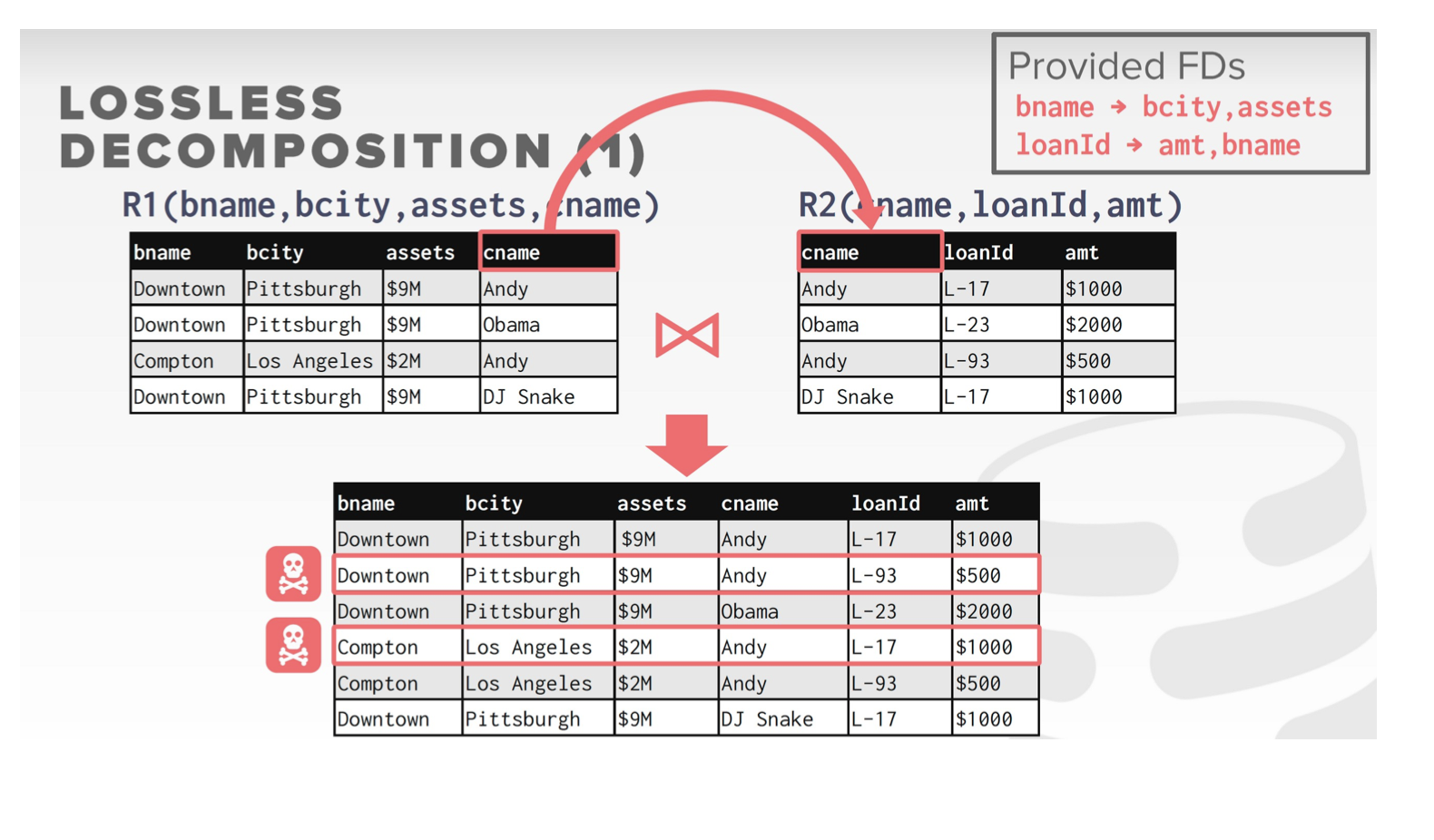
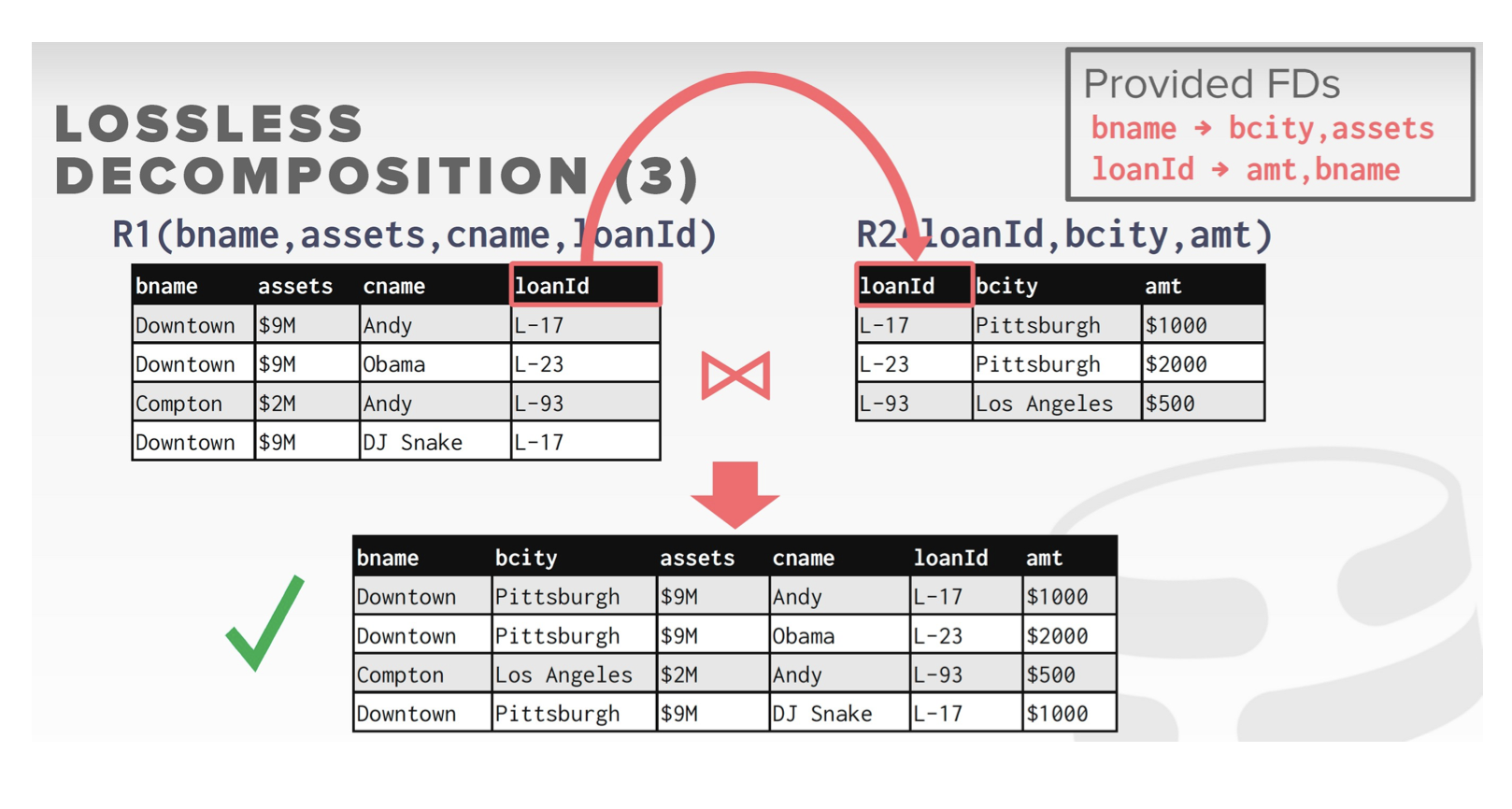
Decomposition:

Suppose we had started with inst_dept. How would we know to split up (decompose) it into instructor and department?

All attributes of an original schema (R) must appear in the decomposition (R1, R2)

Lossless-join decomposition.
 For all possible relations r on Schema R

 

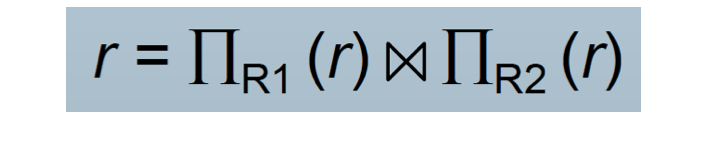
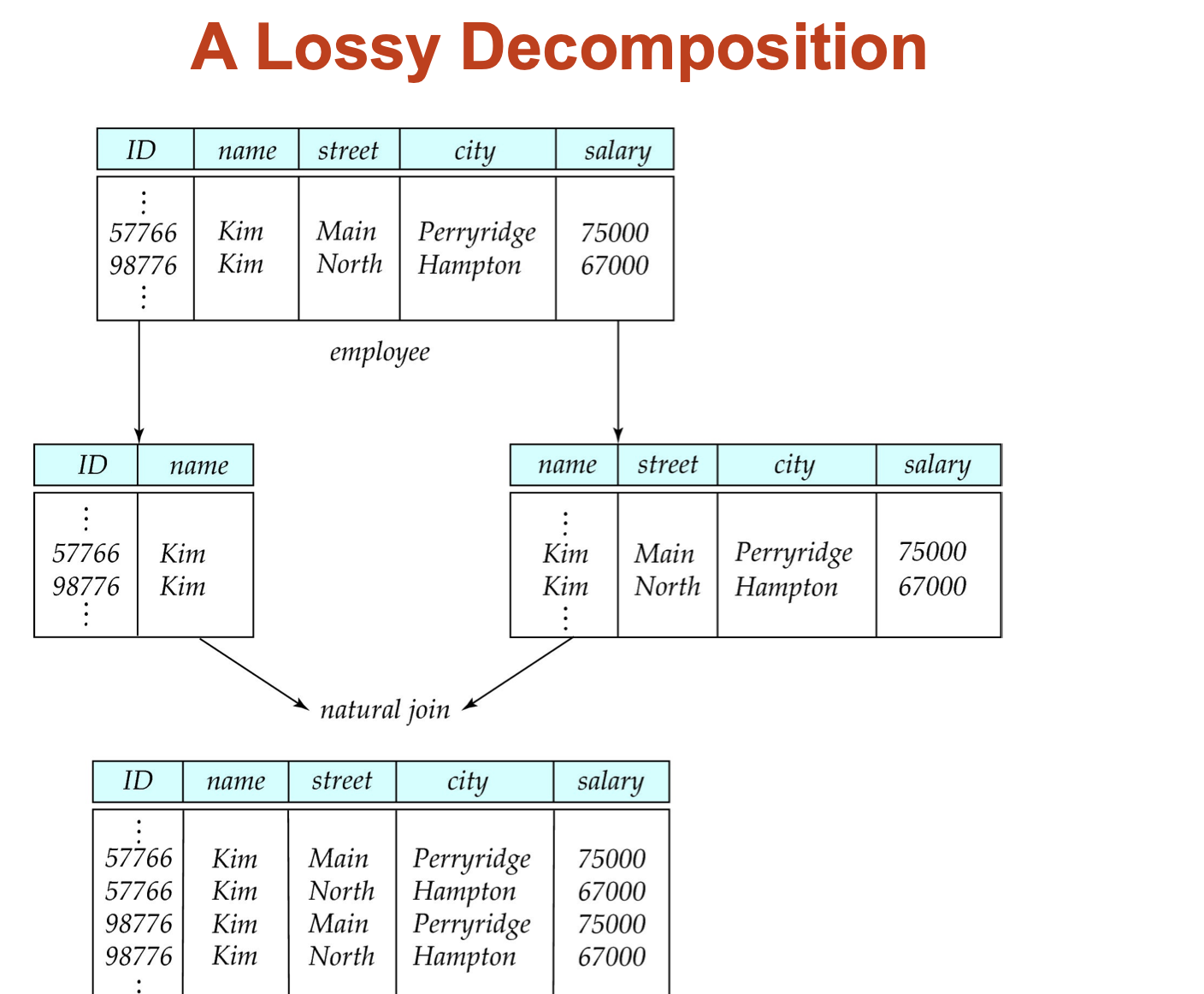
Not all decompositions are good. Suppose we decompose employee(ID, name, street, city, salary) into

employee1 (ID, name)
employee2 (name, street, city, salary)



The next slide shows how we lose information -- we cannot reconstruct the original employee relation -- and so, this is a lossy decomposition.

Boyce-Codd Normal Form:

A relation schema R is in BCNF with respect to a set F of functional dependencies if for all functional dependencies in F+ of the form

α->β

where α\in R and β \in R, at least one of the following holds

α->β is trivial, (i.e. β \in α )

α is a superkey for R

Example schema not in BCNF:
instr_dept (ID, name, salary, dept_name, building, budget )

because dept_name -> building, budget
holds on instr_dept, but dept_name is not a superkey

 

Decomposing a Schema into BCNF:

Suppose we have a schema R and a non-trivial dependency α->β causes a violation of BCNF.

We decompose R into:

(α \union β)

(R-(β - α))

In our example,

α = dept_name

β = building, budget

and inst_dept is replaced by

(α \union β) = ( dept_name, building, budget )

( R - (α-β) ) = ( ID, name, salary, dept_name )

 

Overall Database Design Process：

We have assumed schema R is given

R could have been generated when converting E-R diagram to a set of tables.

R could have been a single relation containing all attributes that are of interest (called universal relation).

Normalization breaks R into smaller relations.
R could have been the result of some ad hoc design of relations,

which we then test/convert to normal form.