深度学习之前馈神经网络（前向传播和误差反向传播）

这篇文章主要整理三部分内容，一是常见的三种神经网络结构：前馈神经网络、反馈神经网络和图网络；二是整理前馈神经网络中正向传播、误差反向传播和梯度下降的原理；三是梯度消失和梯度爆炸问题的原因及解决思路。

一、神经网络结构

目前比较常用的神经网络结构有如下三种：

1、前馈神经网络

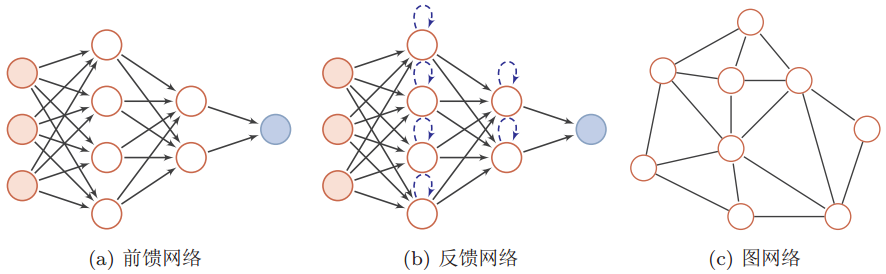
前馈神经网络中，把每个神经元按接收信息的先后分为不同的组，每一组可以看做是一个神经层。每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元。整个网络中的信息是朝着一个方向传播的，没有反向的信息传播（和误差反向传播不是一回事），可以用一个有向无环图来表示。

前馈神经网络包括全连接前馈神经网络和卷积神经网络。

前馈神经网络可以看做是一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。

2、反馈神经网络

反馈神经网络中神经元不但可以接收其他神经元的信号，而且可以接收自己的反馈信号。和前馈神经网络相比，反馈神经网络中的神经元具有记忆功能，在不同时刻具有不同的状态。反馈神经网络中的信息传播可以是单向也可以是双向传播，因此可以用一个有向循环图或者无向图来表示。

常见的反馈神经网络包括循环神经网络、Hopfield网络和玻尔兹曼机。

而为了进一步增强记忆网络的记忆容量，可以映入外部记忆单元和读写机制，用来保存一些网络的中间状态，称为记忆增强网络，比如神经图灵机。

3、图网络

前馈神经网络和反馈神经网络的输入都可表示为向量或者向量序列，但实际应用中很多数据都是图结构的数据，比如知识图谱、社交网络和分子网络等。这时就需要用到图网络来进行处理。

图网络是定义在图结构数据上的神经网络，图中每个结点都由一个或者一组神经元组成。结点之前的连接可以是有向的，也可以是无向的。每个结点可以收到来自相邻结点或自身的信息。

以下是这三种神经网络结构的示意图：

 

二、前馈神经网络

在前馈神经网络（Feedforward Neural Network， FNN ）中，每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层叫做输入层，最后一层叫做输出层，其他中间层叫做隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。

多层前馈神经网络的图示如下：

1、前馈神经网络的前向传播

用下面的记号来描述一个前馈神经网络：

前馈神经网络通过下面公式进行信息传播：

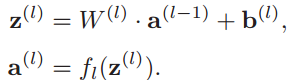
这样前馈神经网络通过逐层的信息传递，得到网络最后的输出a^(L)。整个网络可以看做是一个复合函数，将向量x作为第1层的输入a⁽⁰⁾，将第L层的输出a^(L)作为整个函数的输出。

 2、前馈神经网络的梯度下降法

神经网络具有极其强大的拟合能力，可以作为一个万能函数来使用，通过进行复杂的特征转换，可以以任意精度来近似任何一个有界闭集函数。

类似于其他机器学习算法求解参数的数值计算方法，我们首先考虑用梯度下降法来进行参数学习。

如果采用交叉熵损失函数，对于样本(x,y)，其损失函数为：

其中y∈{0, 1}^C是标签y对应的one-hot向量表示，C是类别的个数。

给定训练集D={(x⁽¹⁾, y⁽¹⁾),(x⁽²⁾, y⁽²⁾),...,(x^(N), y^(N))}，将每个样本x⁽ⁿ⁾输入给前馈神经网络，得到神经网络的输出后，其在训练集D上的结构化风险函数为：

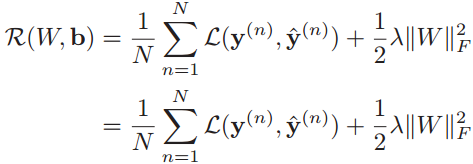
其中W和b分别表示网络中所有的权重矩阵和偏置向量。是正则化项，公式为：

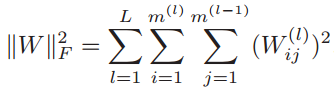
然后用梯度下降法来进行学习。在梯度下降法的每次迭代中，第l层的参数W^(l)和b^(l)的参数更新方式为：

梯度下降法需要计算损失函数对参数的偏导数，如果用链式法则对每个参数逐一求偏导，涉及到矩阵微分，效率比较低。所以在神经网络中经常使用反向传播算法来高效地计算梯度。

 3、前馈神经网络的误差反向传播算法

假设给定一个样本（x,y），将其输入到神经网络模型中，得到损失函数为：，如果要采用梯度下降法对神经网络的参数进行学习，那么就要计算损失函数关于每个参数的导数。

我们就拿第l层中的参数矩阵W^(l)和b^(l)为例，计算损失函数对参数矩阵的偏导数。但因为的计算涉及到矩阵微分，非常繁琐，于是我们先计算W^(l)中某个元素的偏导数。根据链式法则有：

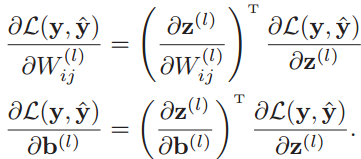
上面两个公式中的第二项都是目标函数关于第l层的神经元z^(l)的偏导数，称为误差项。那么我们需要计算三个偏导数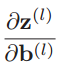：，和。

（1）计算偏导数

由于z^(l)和W_ij^(l)的函数关系为，所以偏导数为

 其中W_i:^(l)为权重矩阵W^(l)的第i行。

（2）计算偏导数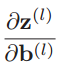

因为z^(l)与b^(l)的函数关系为，因此偏导数是一个维度是m^(l) × m^(l) 的单位矩阵。

 （3）计算误差项

用δ^(l)来定义第l层神经元的误差项，它用来表示第l层神经元对最终损失的影响，也反映了最终损失对第l层神经元的敏感程度。

根据链式法则，第l层的误差项为：

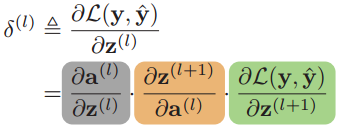
首先根据，其中f_l(•)是按位计算的函数，计算的偏导数如下。diag(•)表示对角矩阵。

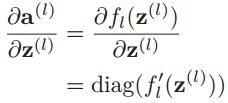
然后根据，有：

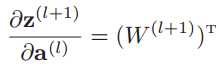
于是第l层的误差项δ^(l)最终表示为：

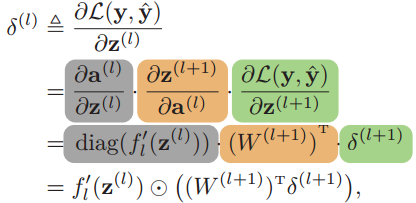
其中⊙表示向量的点积运算符，表示每个元素相乘。

上面这个公式就是误差的反向传播公式！因为第l层的误差项可以通过第l+1层的误差项计算得到。反向传播算法的含义是：第l层的一个神经元的误差项等于该神经元激活函数的梯度，再乘上所有与该神经元相连接的第l+1层的神经元的误差项的权重和。

再回到开头求两个参数的公式：

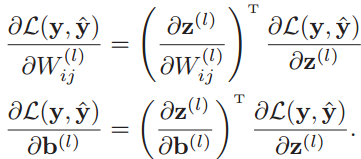
里面的三个偏导数都已经求出来了。于是可以求出：

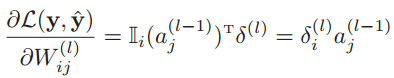
进一步，损失函数关于第l层权重W^(l)梯度为：

而损失函数关于第l层偏置b^(l)的梯度为：

于是在利用误差反向传播算法计算出每一层的误差项后，就可以得到每一层参数的梯度。

基于误差反向传播算法（backpropagation，BP）的前馈神经网络训练过程可以分为以下三步：

1、在前向传播时计算每一层的净输入z^(l)和激活值a^(l)，直至最后一层；

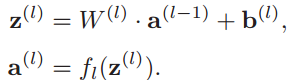
2、用误差反向传播计算每一层的误差项 δ^(l)；

3、计算每一层参数的偏导数，并更新参数。

使用随机梯度下降的误差反向传播算法的具体训练过程如下：

 

三、梯度消失和梯度爆炸

训练神经网络，尤其是深度神经网络时，面临的一个问题是梯度消失或者梯度爆炸，也就是神经元上的梯度会变得非常小或者非常大，从而加大训练的难度。

1、原理

梯度消失（Vanishing Gradient Problem，或称梯度弥散）的意思是，在误差反向传播的过程中，误差经过每一层传递都会不断衰减，当网络层数很深时，神经元上的梯度也会不断衰减，导致前面的隐含层神经元的学习速度慢于后面隐含层上的神经元。

在上面我们得到了神经网络中误差反向传播的迭代公式：

误差从输出层反向传播时，在每一层都要乘以该层的激活函数的导数，如果导数的值域小于1，甚至如Sigmoid函数在两端的饱和区导数趋于0，那么梯度就会不断衰减甚至消失。

与之相对的问题是梯度爆炸（Exploding Gradient Problem），也就是前面层中神经元的梯度变得非常大。与梯度消失不太一样的是，梯度爆炸通常产生于过大的权重W。

总结一下就是：梯度消失通常出现在深层网络和采用了不合适的损失函数（sigmoid）的情形，梯度爆炸一般出现在深层网络和权值初始化值太大的情况下。

2、举例

可以通过一个例子来更好的理解这两个问题。来看一个简单的深度神经网络：每一层都只有一个神经元。如下图是有三层隐含层的神经网络：

这里w表示权重，b是偏置值，C是代价函数。然后通过计算代价函数关于第一个隐含神经元的偏置的梯度，以及关于第三个隐含神经元偏置的梯度，来考察梯度消失和梯度爆炸问题。

经过推导可得梯度的公式：

（1）梯度消失

首先看公式中的导数σ^'(z)。激活函数如果采用Sigmoid函数，则其导数为：，也就是说导数的最大值为0.25。

其次看公式中的权重w。如果用均值为0标准差为1的高斯分布来初始化网络的权重，那么所有的权重会满足|w_j|<1。

那么就会与w_jσ^'(z_j)<0.25，于是梯度公式中所有项相乘时，梯度以指数级下降；神经网络的层数越深，梯度的值下降得更快。

然后再与第三个隐含神经元的梯度进行对比，如下图。可见前面的神经元的偏置的梯度是后面的1/16甚至更小。所以梯度消失产生的原因主要就是激活函数的导数值太小。

 （2）梯度爆炸

梯度爆炸的一个原因是网络的权重设置得过大，比如在上图中，让w_j=100 。然后选择偏置使得σ^'(z_j)项不会太小，比如σ^'(z_j)=0.25，那么w_jσ^'(z_j)=25。代入上面的梯度公式中，可以看到梯度以25的指数级增大，神经网络的层数越深，梯度越大。这就带来了梯度爆炸的问题。

 3、解决

那么如何解决梯度消失和梯度爆炸的问题呢？

一般用以下几种方法来解决梯度消失和梯度爆炸的问题。

（1）对于梯度消失问题，可以选择导数比较大的激活函数，比如ReLU激活函数。

Sigmoid函数和Tanh函数都属于两端饱和型激活函数，使用这两种激活函数的神经网络，在训练过程中梯度通常会消失，因此可以选择其他激活函数来替代。

ReLU激活函数在正数部分的导数恒为1，每层网络都可以得到相同的更新速度，因此在深层网络中不会产生梯度消失和梯度爆炸的问题。

（2）对于梯度爆炸问题，可以采取梯度截断和权重正则化的方法。

梯度截断这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度截断阈值，然后在更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。

权重正则化就是在损失函数中，加入对网络的权重进行惩罚的正则化项，比如权重的L₁正则化或者L₂正则化。如果发生梯度爆炸，权值的范数会变得非常大，通过正则化项进行惩罚，可以限制权重的值，从而减轻梯度爆炸的问题。

（3）选择更好的随机初始化权重的方法。

一是对每个权重都进行随机初始化，尽量让每个权重都不同，使不同神经元之间的区分性更好。

二是选择合适的随机初始化权重的区间，不能太小，也不能太大。一般而言，参数初始化的区间应该根据神经元的性质进行差异化的设置，如果一个神经元的输入连接很多，那么每个输入连接上的权重要小一些，以避免神经元的输出过大（当激活函数为ReLU时，但输出为正时导数都是1）或者过饱和（当激活函数为Sigmoid函数时，梯度会接近于0）

此外，还有Batchnorm（batch normalization）的方法，留待以后探究。

 

 

 

 

参考资料：

1、邱锡鹏：《神经网络与深度学习》

2、Michael Nielsen：《Neural Network and Deep Learning》