图的应用 2-行车路线

图的应用 2-行车路线

一、问题分析

【问题描述】

小明和小芳出去乡村玩，小明负责开车，小芳来导航。

小芳将可能的道路分为大道和小道。大道比较好走，每走 1 公里小明会增加

1 的疲劳度。小道不好走，如果走小道，小明的疲劳值会快速增加，走 s 公里小

明会增加 s2 的疲劳度。所有的小道不相交。

例如：有 5 个路口，1 号路口到 2 号路口为小道，2 号路口到 3 号路口为大

道，3 号路口到 4 号路口为大道，4 号路口到 5 号路口为小道，相邻路口之间的

距离都是 2 公里。如果小明从 1 号路口到 5 号路口，则总疲劳值为 22+2+2+22=4

+2+2+4=12。

现在小芳拿到了地图，请帮助她规划一个开车的路线，使得按这个路线开车

小明的疲劳度最小。

【输入形式】

输入的第一行包含两个整数 n, m，分别表示路口的数量和道路的数量。路

口由 1 至 n 编号，小明需要开车从 1 号路口到 n 号路口。

接下来 m 行描述道路，每行包含四个整数 t, a, b,

c，表示一条类型为

t，连接 a 与 b 两个路口，长度为 c 公里的双向道路。其中 t 为 0 表示大道，t

为 1 表示小道。保证 1 号路口和 n 号路口是连通的。

【输出形式】

输出一个整数，表示最优路线下小明的疲劳度。

【样例输入】

输入：

6 7

1 1 2 3

0 2 3 2

0 1 3 30

0 3 4 20

0 4 5 30

1 3 5 6

0 5 6 1【样例输出】

48

【数据规模和约定】

对于 25%的评测用例，不存在小道；

对于所有评测用例，

1 ≤ n

≤ 8，

1 ≤ m

≤ 10，

1 ≤ a, b

≤ n，

t 是 0 或 1，c

≤ 100。保证答案不超过 100。

二、数据结构和算法设计

1)

图的抽象数据类型设计：

数据对象：G（

V,S）

2)

物理数据对象设计（不用给出基本操作的实现

数据关系：采用邻接矩阵存储图的元素。用 Dijsktra 算法改进计算最

短路径。

基本实现：

初始化：void Init(int n);

顶点数：int n();

边数：int e();

第一个临接顶点：int first(int v);

下一个临接顶点：int next(int v,int w);

建边：void setEdge(int v1,int v2,int wght);

删除边：void delEdge(int v1,int v2);

判断两点间是否有边：bool isEdge(int i,int j);取边的权值：int weight(int v1,int v2);

返回顶点的标记值：char getMark(int v);

标记顶点： void setMark(int v,int val);

最短路径算法:void Dijkstra(Graph*G,int *D,int s);

3)

算法思想的设计

用队列存储图的元素，处理第一个顶点 V，若该顶点未被标记。取连

接顶点 V 和 V1 上的边，再处理顶点 V2 时，考虑从顶点 V 到 V2 的最

短路径长度。本体要求区分大路和小路，若为小路取 s2。依次继续

遍历，直至遍历所有的顶点。

4)

请用题目中样例，基于所设计的算法，详细给出样例求解过程。

1

图的邻接矩阵记录边和顶点的信息

void setEdge(int v1,int v2,int wt)

{

if(wt<=0)

{

cout<<"Illegal weight value";

}

else

{if(matrix[v1][v2]==0)

{

numEdge++;

}

matrix[v1][v2]=wt;

}

}

2 Dijsktra 算法

 

 

 

 

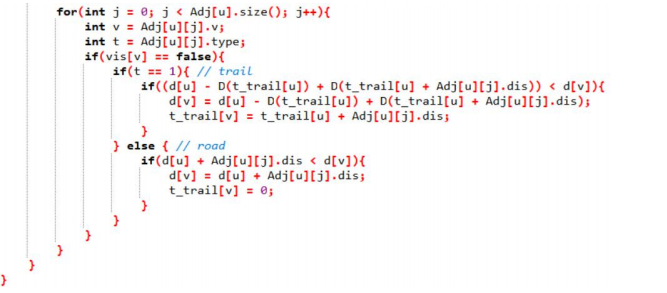
3. 输出最短路径长度

 

 

5) 关键功能的算法步骤

从第一个顶点开始，取其下一顶点最短的边并记录；

取下一顶点，判断从起始顶点到此顶点的最短路径长度，并标记；

依次类推，直至标记完所有的顶点。

三、算法性能分析

1)setEdge（）操作是对所有边进行记录，算法复杂度 O(|D|)

2)Dijsktra()操作是对图的节点进行遍历，算法复杂度为 O(|V|)

四．测试