从[SDOI2011]消防 到[NOIP2007]树网的核

有关消防一题中最优解一定在直径上的证明
P2491 [SDOI2011] 消防
P1099 [NOIP2007 提高组] 树网的核

题目描述

在一颗 \(n\) 个节点的无根树中，找到一条不超过 \(s\) 的路径，使得图中所有点到此路径距离的最大值最小，图中边权非负

分析

若想将此题转化到树网的核，需要证明对于任意一条不在直径上的路径，都能在直径上找到更优解
首先理解一个显然的结论：路径越长，结果越优

证明

以下过程中所用符号及其含义:

• \(f(i)\) 表示从 \(i\) 出发不经过直径上的边所能到达的最长距离
• \((u, v)\) 为树的直径, \(L\) 为直径长度
• \((A, B)\) 为所取不在直径上的路径
• \(d(i, j)\) 为 \(i\) 与 \(j\) 间的路径长
  
  

Part 1 : 所选路径与直径有交集

根据直径的最长性，很容易得到如下性质：

1. 对于 \((A, C)\) 路径上的每一点\(i\), 都有\(f(i) \leq d(u, C)\)

如果大于，那么 $ f(i) + d(i, v) > L$, 与直径的最长性矛盾

2. 对于\((D, B)\) 路径上的每一点 \(i\), 都有\(f(i) \leq d(D, v)\)

---

通过观察发现，只需截取 \((C, D)\) 就能满足1，2两条性质
由此我们可以将 \((A, C)\) 和 \((D, B)\) 称作是多余的，完全可以将\(AC, DB\) 的长度转化到直径上获得更优解


第一部分证毕。

Part 2 : 所选路径与直径无交集

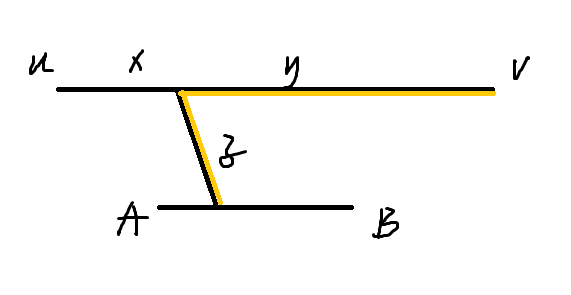
\(x \leq y\) ， \(y \geq \dfrac{L} {2}\)

设 \(val1\) 为图中所有点到 \(AB\) 的最大距离，则一定有

$$val1 = y + z $$

考虑用反证法证明：假设存在点 \(C\)，使得 \(C\) 到 \(AB\) 的距离大于 \(val1\)

其中 \(C\) 到 \(AB\) 距离的最小值 $$d = val1 + 1$$
为了保证不重不漏，我们也把 \(C\) 到 \(AB\) 的路径划分为经过直径与不经过直径两类

case 1：

$ d + z + y > L $ 矛盾

case 2：

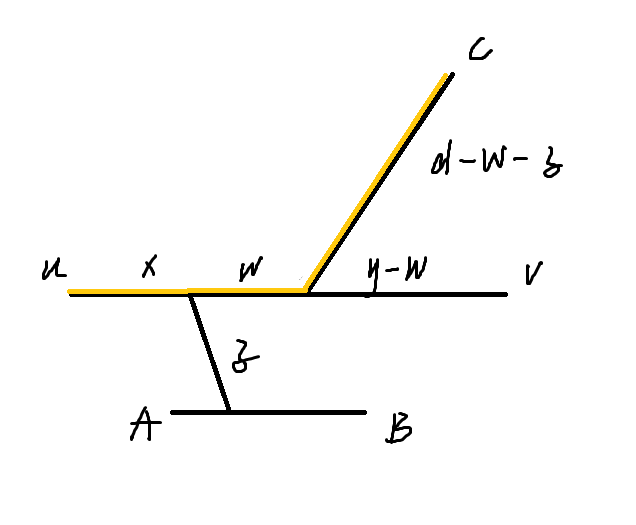
\((d - w - z) + (x + w) = x + y + 1 > L\) 矛盾

因此 $ val1 = y + z $ 得证。

构造更优解

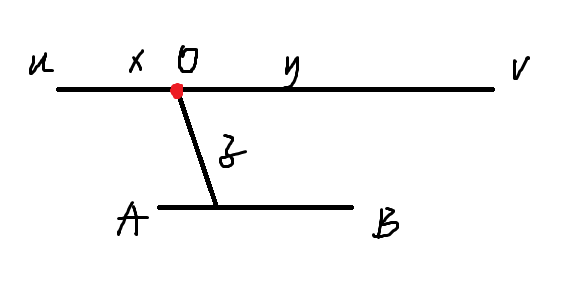
考虑在原图中只取点 \(O\) 作为所选路径
根据定义

\[val2 = max(x, y, f(O)) = y \]

$f(O) \leq \dfrac{L}{2} $

整理一下

\[va1 = y + z, val2 = y \]

\[val2 \leq val1 \]

第二部分证毕。
由于 \(z\) 可以取到0, 一种更严谨的说法是：对于任意一条与直径不相交的路径都不能在直径上构造出次优解

AC代码

#include<bits/stdc++.h>
#define ll long long

using namespace std;
const ll N = 5e5 + 5;

int n, vis[N], a[N];
ll s, d[N], sum[N];

vector<pair<int, ll> > H[N];
pair<int, ll> pre[N];

int bfs(int source) {
	memset(d, -1, sizeof d);
	queue<int> q;
	q.push(source);
	d[source] = 0;
	while(!q.empty()) {
		int x = q.front();
		q.pop();
		for(auto [y, z] : H[x]) {
			if(d[y] == -1) {
				d[y] = d[x] + z;
				pre[y] = {x, z};
				q.push(y);
			}
		}
	}
	int ret = source;
	for(int i = 1; i <= n; ++ i) {
		if(d[ret] < d[i]) ret = i;
	}
	return ret;
}

void dfs(int x) {
	vis[x] = 1, d[x] = 0;
	for(auto [y, z] : H[x]) {
		if(vis[y]) continue;
		dfs(y);
		d[x] = max(d[x], d[y] + z);
	} 
}

int main() {
	ios :: sync_with_stdio(0);
	cin.tie(nullptr);
	cin >> n >> s;
	for(int i = 1, x, y, z; i < n; ++ i) {
		cin >> x >> y >> z;
		H[x].push_back({y, z});
		H[y].push_back({x, z});
	}
	int u = bfs(1);
	int v = bfs(u);
	int p = v, idx; ll maxd = -2e9, ans = 2e9;
	while(p != u) {
		a[++ idx] = p;
		p = pre[p].first;
	}
	a[++ idx] = u;
	for(int i = 1; i <= idx; ++ i) vis[a[i]] = 1;
	for(int i = 1; i <= idx; ++ i) {
		dfs(a[i]);
		sum[i] = sum[i - 1] + pre[a[i - 1]].second;
		maxd = max(maxd, d[a[i]]);
	}
	for(int i = 1, j = 1; i <= idx; ++ i) {
		while(sum[j + 1] - sum[i] <= s && j < idx) ++ j;
		ans = min(ans, max({maxd, sum[i], sum[idx] - sum[j]}));
	}
	cout << ans;
	return 0;
}