BUAA_OO_Unit1_Summary
目录
-
程序结构分析
-
第一次作业
-
-
第三次作业
-
-
度量分析
-
规模分析
-
复杂度分析
-
UML
-
-
Bug分析与测试策略
-
Bug分析
-
测试策略
-
-
心得体会
一、程序结构分析
第一次作业
-
设计要求:
读入一个包含加、减、乘、乘方、括号、数字、空白字符、x的表达式(其中括号深度最大为一),对其进行化简并输出所得表达式。
-
思路简述
整体设计思路参考了第一次训练中给出的递归下降思路,将一个表达式分为Expr, Term, Factor,之后设计方法将其化简合并,得到答案。
设置常数类Number,幂函数类PowerFunc,Term由常数与幂函数相乘得到,Expr由Term相加的到。其中对于正负号的处理,我们在Term类中设置一个布尔类型变量negative用来标记该项是正数还是负数。由于拆括号等工作在递归下降中不难完成,在此就不再叙述。
至此解析过程基本结束,接下来是合并过程。
我们知道,表达式是由项组成的,项可以是常数,可以是幂函数,也可以是二者的乘积。也就是说,所有的项都可以用这样的形式来表示——a*x^b所以我们干脆创建一个新的类将二者囊括在内,我们将其命名为PolyTerm类,其包含了两个属性,系数和指数,这样就完美的存储了项这一概念。
为了处理这些项,我们另外创建一个方法类Polynomial,并在其中设置HashMap<int, PolyTerm>储存PolyTerm,设计了一定方法用以处理多个项之间的乘法,合并等问题,之后在主类中只需要将其依次相加并输出即可。
这一设计思路也是我在三次设计之中沿用的思路,在后续过程中根据设计需求进行了
大面积重构适当的完善。对于优化方面,对于1*x不输出1这类小问题进行了优化,但是秉持着功能大于性能的思想
(害怕出错+懒)本人并未处理x**2=x * x之类的优化,毕竟这些都是小问题,性能分也高不了两分。(“我宁愿什么都不做,也不愿犯错”
第二次作业
-
设计要求
在第一次作业基础上添加了sin,cos,sum函数以及自定义函数,其中sin和cos括号内部仅有可能出现常数和幂函数,非必要括号深度为一层,也不会出现函数嵌套的情况。
-
思路简述
整体上思路和第一次作业相似,递归下降处理表达式之后化简合并输出。但是也需要单独处理三角函数,求和函数和自定义函数。
在本次作业中笔者处理问题的关键体现在“取 舍”二字,对于新增的三种类型,我们毫无疑问都需要处理。那么在哪里处理呢?
我们知道,能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为其他形式,或者从一个物体转移到另一个物体,在转化或转移的过程中,能量的总量不变。
这就是能量守恒定律。
我们可以将程序看成两个部分,前者是解析处理,或者是化简合并,显然,我们要处理一个问题,如果在前期简化处理部分,那么后期化简合并就会变得复杂;如果在前期着重处理,那么后期化简合并就会相对简单。
在本次作业中,笔者采取了前期进行详尽的表达式替换,包括三角函数的次方展开,sum函数展开,自定义函数展开等,处理完成后向后续化简合并程序传入了一个仅包含一系列简单项的表达式,这样也可以避免对第一次作业的化简程序进行大规模重构。
对于三角函数,笔者的处理方法是新建一个TrigFunc类,并在递归下降的过程中单独设置一个方法PraseTrig,在PraseFactor读取到三件函数时进行处理。同时为了将其解析合并,笔者一定程度上重构了PolyTerm类和其对应的方法类Polynomial类。在PolyTerm中新增了
ArrayList<String> sinExpr 和ArrayList<String> cosExpr,用以储存项中的所有三角函数。在Polynomial中对HashMap进行了改造,设置新的Key类,属性为sinExpr,cosExpr和指数,HashMap变为HashMap<Key, PolyTerm>,其余处理类似第一次作业,不再赘述。
对于sum函数,笔者采用了表达式替换的操作,通过正则表达式取出sum函数,并对其进行替换得到常规表达式,即可免去后续过程如递归下降中处理该函数的问题。
对于自定义函数,同样采取表达式替换的方式,新建CusFunc类,设置添加自定义函数和解析自定义函数方法,读取时添加自定义函数,解析时替换自定义函数,即可完成对于自定义函数的处理。
值得注意的是,在表达式替换当中需要在最外层添加括号,不然很可能出现不知名bug。但是添加了过多的括号看起来不太妙,处理过程岂不变得十分繁琐?当然不是,递归下降算法最不怕的就是括号,于是我们只需要快乐的添加括号即可。
第三次作业
-
设计要求
在第二次作业的基础上支持了多层括号嵌套,函数之间的相互调用功能,函数的嵌套运算。
-
思路简述
本次作业之中,并未添加新的变量,但是放宽了限制条件,允许函数间调用,嵌套,这就导致了解析表达式变得复杂,显然手动判断解析难以满足我们的需求,毕竟嵌套理论上是无限的,这时候就需要选择递归的调用解析。
对于自定义函数,我们采用表达式替换的方式,照搬第二次作业的方式。这时候就有人会问了,那出现函数嵌套,像f(g(x))怎么办呢?好办,再来一次表达式替换,不就把内层函数也替换掉啦。又有人要问了,你这个不行,要是出现f(g(f(g(f(g(f(g(f(g(x))))))))))怎么办呢?那就用一个while循环把他反复处理,直到处理前后字符串不再发生变化为止。虽然很笨,复杂度不低,但是很简单。
(我不信会TLE对于三角函数嵌套问题,笔者认为是第三次作业中最重要的问题。其他的问题如自定义函数嵌套,都可以在预处理阶段解决,不会干扰后续处理。但是如果我们把三角函数处理方式照搬第二次作业,读到sin或者cos就把括号内的内容设为三角函数类属性content,固然可以,但是内部的化简就无法进行。
不得不承认,笔者确实是懒,但是如果草率的放在这里,就不只是性能分的问题,还涉及到了内部出现多余括号的问题,也就是正确性都无法保证,这是无法接受的。
那么如何处理呢?显然是递归。我们把内部content也视为表达式,调用之前的解析处理函数对这一表达式进行处理,就完美的完成了这个问题。除此之外,我们惊奇的发现,这一串代码不仅仅是处理content,而且可以处理content中的content,因为这是一个递归的调用。
尽管写的时候并没有想到,结果跑出来结果出乎意料的妙至此,第三次作业的任务基本就完成了。
二、度量分析
规模分析
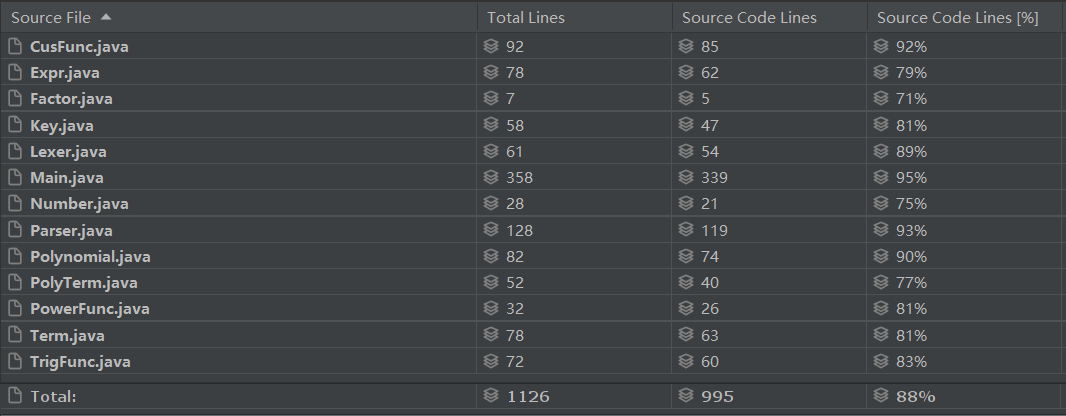
复杂度分析
OCavg = Average operation complexity(平均操作复杂度)
OCmax = Maximum operation complexity(最大操作复杂度)
WMC = Weighted method complexity(加权方法复杂度)
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| expression.CusFunc | 3.2 | 9.0 | 16.0 |
| expression.Expr | 1.7142857142857142 | 5.0 | 12.0 |
| expression.Number | 1.0 | 1.0 | 3.0 |
| expression.PowerFunc | 1.3333333333333333 | 2.0 | 4.0 |
| expression.Term | 1.8571428571428572 | 4.0 | 13.0 |
| expression.TrigFunc | 1.2222222222222223 | 2.0 | 11.0 |
| Lexer | 2.75 | 7.0 | 11.0 |
| Main | 7.181818181818182 | 13.0 | 79.0 |
| Parser | 4.4 | 9.0 | 22.0 |
| poly.Key | 1.2222222222222223 | 3.0 | 11.0 |
| poly.Polynomial | 3.0 | 7.0 | 15.0 |
| poly.PolyTerm | 1.0 | 1.0 | 9.0 |
| Total | 206.0 | ||
| Average | 2.675324675324675 | 5.25 | 17.166666666666668 |
显然,由上图可以得到,大量的预处理会导致Main类中复杂度较大,同样,递归下降操作也导致了Parser中复杂度较大。
CogC:cognitive complexity 认知复杂度,表征代码可读性
ev(G):Essential cyclomatic complexity 基本圈复杂度
iv(G):Design complexity 设计复杂度
v(G):cyclonmatic complexity 圈复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| poly.PolyTerm.setSinExpr(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.setExponential(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.setCosExpr(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.setCoefficient(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.PolyTerm(ArrayList, ArrayList, BigInteger, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.getSinExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.getExponential() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.getCosExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.PolyTerm.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Polynomial.setPolyTerms(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Polynomial.multiply(Polynomial, Polynomial) | 15.0 | 1.0 | 7.0 | 7.0 |
| poly.Polynomial.merge(Polynomial) | 5.0 | 1.0 | 4.0 | 4.0 |
| poly.Polynomial.getPolyTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Polynomial.add(Polynomial, Polynomial) | 1.0 | 1.0 | 2.0 | 2.0 |
| poly.Key.setSinExpr(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.setExponential(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.setCosExpr(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.Key(ArrayList, ArrayList, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.getSinExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.getExponential() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.getCosExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| poly.Key.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| Parser.parseTrig() | 5.0 | 1.0 | 3.0 | 5.0 |
| Parser.parseTerm() | 3.0 | 1.0 | 3.0 | 3.0 |
| Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseFactor() | 18.0 | 5.0 | 11.0 | 11.0 |
| Parser.parseExpr() | 7.0 | 1.0 | 5.0 | 5.0 |
| Main.sumExtend(char, BigInteger, BigInteger, String) | 15.0 | 1.0 | 8.0 | 8.0 |
| Main.powerExtend(int, String, StringBuilder) | 50.0 | 1.0 | 16.0 | 16.0 |
| Main.output(String) | 34.0 | 1.0 | 14.0 | 14.0 |
| Main.outExpr(StringBuilder) | 10.0 | 1.0 | 9.0 | 9.0 |
| Main.merge(String, int) | 19.0 | 3.0 | 5.0 | 10.0 |
| Main.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| Main.handle(String, CusFunc) | 34.0 | 9.0 | 20.0 | 21.0 |
| Main.getNum(String, int) | 4.0 | 3.0 | 3.0 | 3.0 |
| Main.findRight(int, String) | 4.0 | 1.0 | 3.0 | 4.0 |
| Main.findLeft(int, StringBuilder) | 4.0 | 1.0 | 3.0 | 4.0 |
| Main.cusExtend(String, CusFunc) | 13.0 | 1.0 | 7.0 | 8.0 |
| Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.next() | 13.0 | 2.0 | 6.0 | 8.0 |
| Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| expression.TrigFunc.TrigFunc(String, int, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.toString() | 2.0 | 2.0 | 1.0 | 2.0 |
| expression.TrigFunc.toPolynomial() | 2.0 | 1.0 | 2.0 | 2.0 |
| expression.TrigFunc.setType(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.setPower(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.setContent(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.getType() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.getPower() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TrigFunc.getContent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.toString() | 4.0 | 1.0 | 3.0 | 4.0 |
| expression.Term.toPolynomial() | 4.0 | 1.0 | 4.0 | 4.0 |
| expression.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.setNegative(boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.getNegative() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.PowerFunc.toString() | 1.0 | 2.0 | 1.0 | 2.0 |
| expression.PowerFunc.toPolynomial() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.PowerFunc.PowerFunc(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Number.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Number.toPolynomial() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Expr.toString() | 6.0 | 1.0 | 5.0 | 5.0 |
| expression.Expr.toPolynomial() | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.Expr.setPower(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Expr.getPower() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Expr.Expr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.CusFunc.setHashMap(HashMap>) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.CusFunc.handle(String) | 18.0 | 4.0 | 8.0 | 10.0 |
| expression.CusFunc.getHashMap() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.CusFunc.CusFunc() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.CusFunc.addFunc(String) | 5.0 | 1.0 | 4.0 | 4.0 |
| Total | 304.0 | 101.0 | 215.0 | 235.0 |
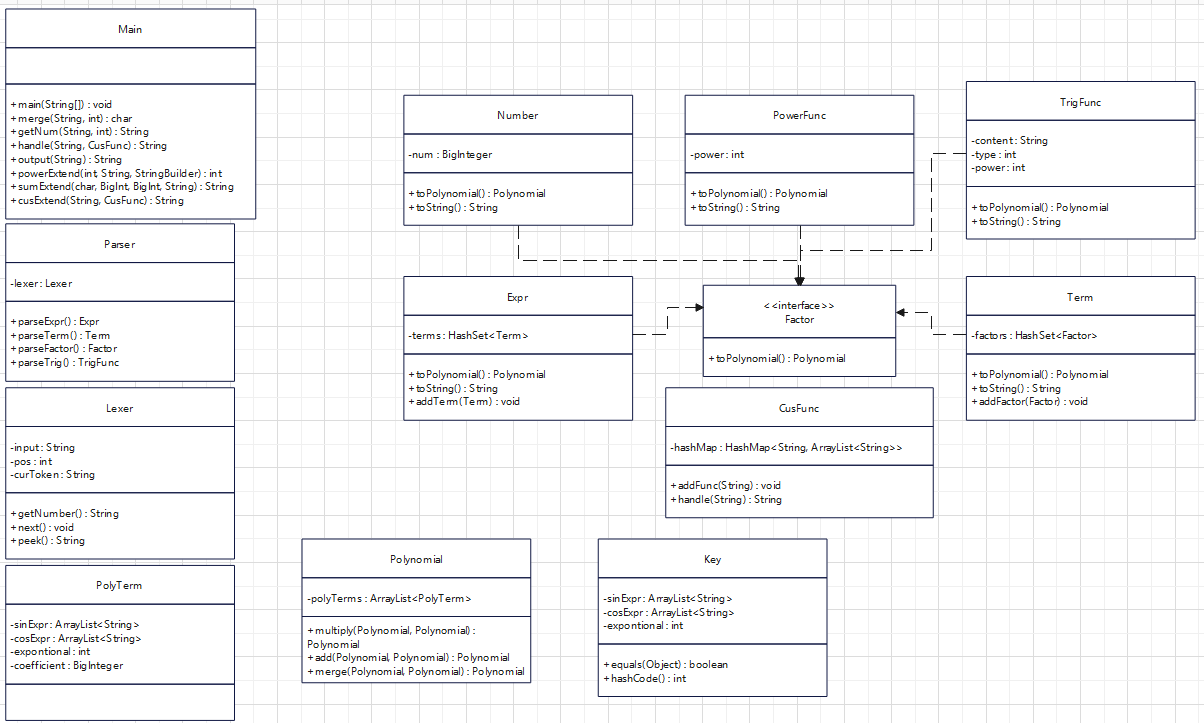
UML
在上面描述每次作业的时候已经将每个类的设计考虑较为详尽的进行了阐释,在这里再简单的叙述一遍。
Main类主要处理输入输出与字符串替换等预处理操作;Parser类与Lexer类一同执行递归下降的解析操作;PolyTerm类描述了一个完整的项所具有的特征属性;Polynomial类主要进行项与项之间的合并化简操作;Factor为接口,围绕接口分别设置了Expr,Term,Number,PowerFunc,TrigFunc类,还有额外的CusFunc类表示自定义函数及其替换等操作。
三、Bug分析与测试策略
Bug分析
-
第一次作业
第一次作业出现了一个bug,原因在于对于1*x = x这类优化处理不当,导致多输出一个+,在公测和互测中都是由于这个问题出现被hack的情况。
-
第二次作业
第二次作业主要问题出现在未考虑输入的自定义函数中存在空白字符的情况,由于中测时给出的样例都是无空格的,所以下意识认为不会有空白字符,结果强测因为这一问题烂掉,但是由于互测不允许输入自定义函数,反而没有被hack到。
-
第三次作业
吸取前两次作业的经验教训,由于第三次作业相对任务量较少,完成后做了充足的测试,并和同学讨论修复了几个小bug,本以为天衣无缝,直到早上起床发现群友给出了sum中包含BigInteger的样例,发现自己又被hack了,天网恢恢,疏而不漏,只能在bug修复时弥补了。
测试策略
-
自测策略
在第一次与第二次测试之中,笔者由于事件原因,都是在周五或周六才完成的作业,由于时间问题
(马上交作业和精力问题(实在肝不动了,仅仅采取了手动构造测试样例和借鉴拿来主义群中或讨论区中的样例进行测试。然而由于测试的样例一般都过于复杂,所以很容易通过。听起来是很奇怪的,为什么样例复杂反而易于通过呢?我们知道,官方的测试是有一定限制的,不会给出复杂度奇高的样例,所以不用太过担心。对于相对复杂的样例,由于大多是通过巨大的数字,多重的乘法,很大的次方实现,虽然看起来很吓人,但是仅仅是吓人而已,以为它考察的仅仅是程序处理常规问题的能力,只要我们搭建的程序可以保证每一个环节都大体正确,那么再巨大的数据也不难处理。
相反,问题往往出现在简单的样例上,因为它考察的是程序处理问题的逻辑。正是细枝末节之处,才更见得水平。例如x-x+1这一样例,再简单不过,很多同学却因为输出问题输出了1+之类的结果,从而导致测试中出错。
在第三次作业的测试中,由于时间相对宽松,笔者参考讨论区中的分享搭建了一个简易的自动化评测机,进行了海量数据的测试,自我感觉保证了正确性,然而仍然出现了bug。
这是由于设计思维上的bug,在主观意识上就并未认识到sum中可以出现大数,在设计评测时自然也不会设计相关样例,跑几万条数据也不可能发现bug。所以多看指导书,多和同学交流也是自测的好办法。
-
互测策略
互测由于有着冷却时间的限制,自然就不能采用随机生成测试样例进行hack。
在OO理论课上,纪老师提到了两个概念,白盒测试和黑盒测试。这时测试的两个主要方向。
先说白盒测试,白盒测试就是指所有的程序细节都展现在你的眼前,你可以阅读代码,寻找漏洞并构造样例进行hack。这时理论上来说最应该采取的方式,不仅可以hack同学,还可以在hack过程中学习对方架构,吸取经验。
然而每次作业房间内都有六七个人,一份份千行代码,设计架构又并不相同,全部阅读实在难度过大,所以在第一次互测之中阅读了两份之后就放弃了该策略。
再说黑盒测试,就是不看待测试程序,直接构造样例进行测试。这一方法的好处在于大大节省了时间,不必再去研究繁杂的程序,坏处在于测试具有很大盲目性,只能猜测可能出现的bug并构造样例。
而在第三次作业中,讨论区出现了一个很有意义的讨论,如何同时hack多个人,即同时将一个样例在多份程序中运行,笔者也采取了这种方法,在第三次作业中对于互测起到了有效的作用。
四、心得体会
-
面向对象思维
在第一单元的作业之中,极大的锻炼了笔者的面向对象思维。这似乎是一句废话,面向对象课程当然是面向对象了,然而在写代码的过程中,面向过程思维仍然时常出现,有时我对室友打趣说,我这简直是JAVA版C语言,面向对象式面向过程。如何抽象出一个个类,一个个方法,这都是十分具有挑战的任务。
-
抗压能力
不得不承认,在开学的第一周OO就给我上了一课,由于寒假过程中美赛等原因,回到学校之后才开始写pre,回来写了几天,到了周四问战哥题的时候他让我赶紧去写作业,我本来以为写一天就差不多了,但是结果好像不是这样。于是周五一大早开始写homework1,然而发现事情并不简单,上午思路全无,但是不写不行了,于是对着训练一开始硬写,参考着讨论区同学的分享,一点点搭建却仍不得要领。直到晚上十一点多看到强生同学的分享,茅塞顿开,于是继续coding至深夜。写到两点实在是熬不住了,早上爬起来继续奋斗,知道下午才终于ac中测,松一口气。
第二周好些,但是也直到周五才完成,第三周倒是非常快的完成了。
-
拿来主义
这个名字听起来很怪,但其实表示的意思就是多学多问。第一周看到强生同学的分享,有一个小地方不懂,于是就加上好友去问,强生同学也热情的给我讲解清楚;第二周研讨课听了张柯同学的报告,其中的设计合并思路也给了我一定灵感;第三次作业讨论区的自动化测试思路,也帮我在自测和互测过程中省了很多力气。“读书人的事,能叫偷吗?”偷学似乎也不是什么难以启齿的事情,何况也并不是偷。
-
可迭代性
三次作业并不是相互独立的,而是层层递进,版版迭代。在第二次作业相信大家已经体会到了,架构的不好可能需要大规模的重构,而架构优秀只需要在原来的基础上进行适当完善即可。当然,笔者并不属于优秀架构的那一部分,然而修修补补,改来改去,也勉强能用,算了放自己一马,就这样将就着用吧。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号