跟着Leo机器学习实战：Logistic回归

一个很有趣的个人博客,不信你来撩 fangzengye.com

跟着Leo机器学习实战：Logistic回归

github

https://github.com/LeoLeos/MachineLearningLeo/tree/master/logRegres

Logistic回归

优点：计算代价不高，易于理解和实现
缺点：容易缺拟合，分类精度不高
适合数据类型：数值型和标称型数据

sigmoid函数以及目标

Logistic回归梯度上升优化算法训练参数

from numpy import *
'''
创建数据数组，和label数组
'''
def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat
def sigmoid(inX):

return 1.0/(1+exp(-inX))
#梯度上升法训练数据

def gradAscent(dataMatIn, classLabels):

dataMatrix = mat(dataMatIn)             #convert to NumPy matrix

labelMat = mat(classLabels).transpose() #convert to NumPy matrix

m,n = shape(dataMatrix)

alpha = 0.001

maxCycles = 500

weights = ones((n,1))       #对每一维即每一列初始化权重

for k in range(maxCycles):              #最大训练次数

h = sigmoid(dataMatrixweights)     #对每一个样本的每一维乘上对应权重求和，再求sigmoid值

error = (labelMat - h)              #与label的误差Nx1列

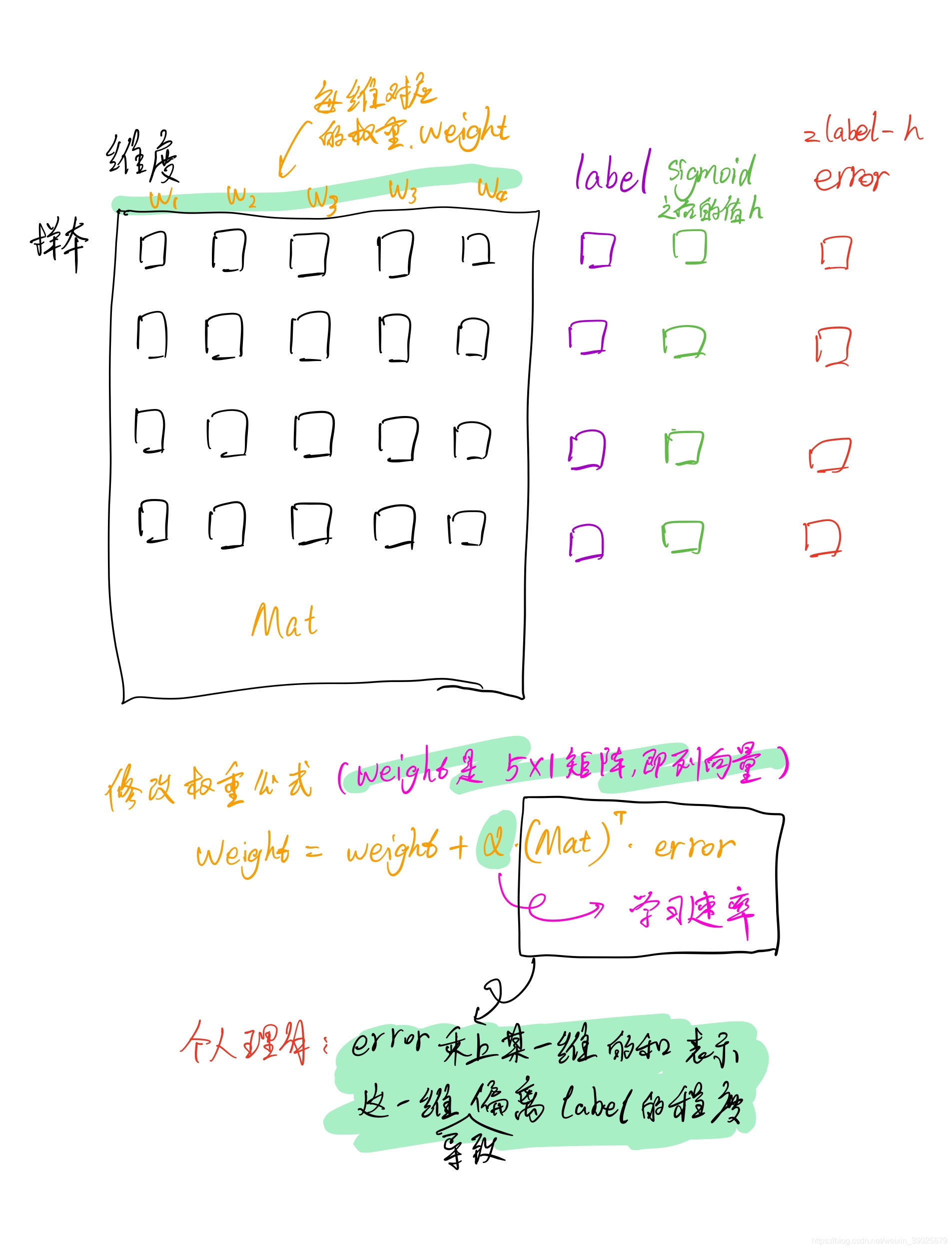
#最重要公式

weights = weights + alpha  dataMatrix.transpose()* error #matrix mult

return weights

训练公式可视化

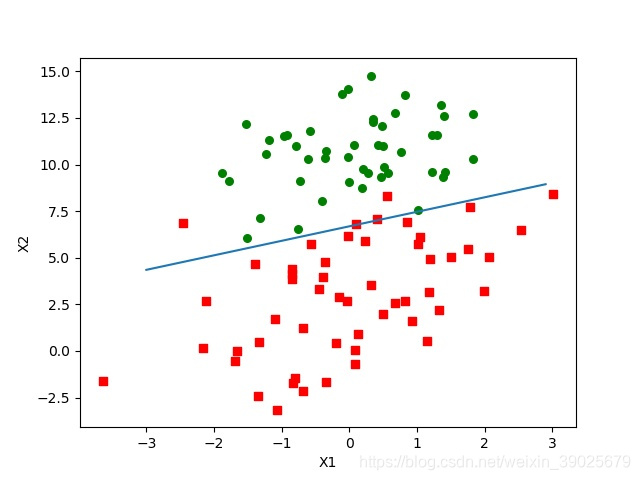
分析数据：画出决策边界（数据可视化）

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat,labelMat=loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0] 
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

训练算法：随机梯度上升

def stocGradAscent0(dataMatrix, classLabels):
   m,n = shape(dataMatrix)
   alpha = 0.01
   weights = ones(n)   #初始化1xN维，与之前不同
   for i in range(m):
       h = sigmoid(sum(dataMatrix[i]*weights))#矩阵才用求和
       error = classLabels[i] - h
       weights = weights + alpha * error * dataMatrix[i]
   return weights      #返回1xN维向量，与之前不同

改进后的随即锑度上升算法

在于随机选取样本来更新权重

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            #模拟退火法alpha逐渐减小
            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not
            #随机选取样本进行更新
            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            #del(dataIndex[randIndex])
    return weights

分类器

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

参考文献

机器学习实战