机器学习多层感知机
一个很有趣的个人博客,不信你来撩http://fangzengye.com
多层感知机
感知机
基本的处理单元
-
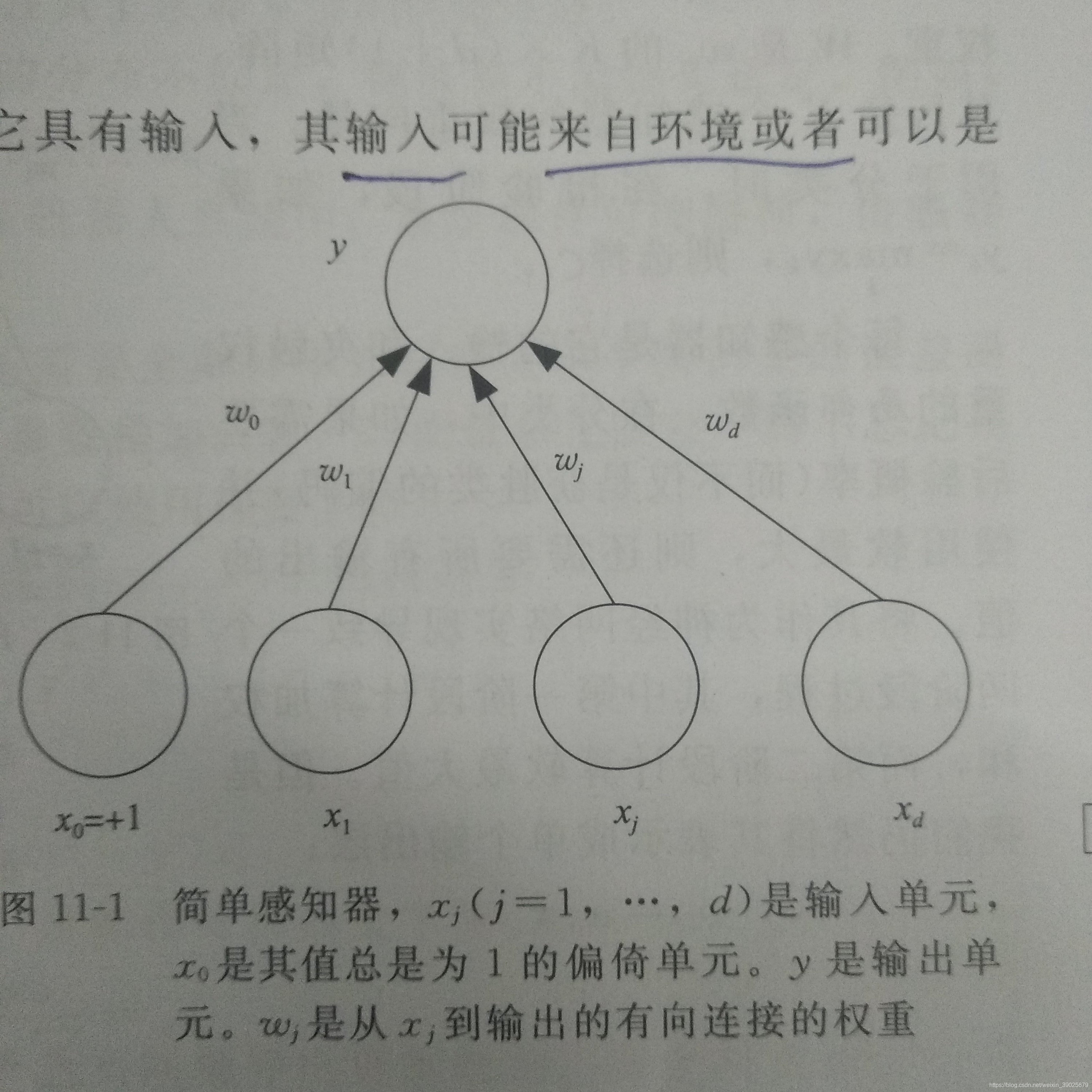
一个感知机
![在这里插入图片描述]()
该感知机的输出 y = w T x y=\textbf{w}^T\textbf{x} y=wTx
w \textbf{w} w维度1x(d+1)
x \textbf{x} x维度(d+1)x1
该公式定义类一个空间超平面,可以将输入空间划分为两个部分。
y = [ w 0 ⋯ w d ] [ x 0 ⋮ x d ] y= \begin{bmatrix} w_0&\cdots&w_d \end{bmatrix} \begin{bmatrix} x_0 \\ \vdots\\ x_d \end{bmatrix} y=[w0⋯wd]⎣⎢⎡x0⋮xd⎦⎥⎤
这是一个感知机单元的输出
假设有多个感知机单元的输出,那表达式会怎样呢? -
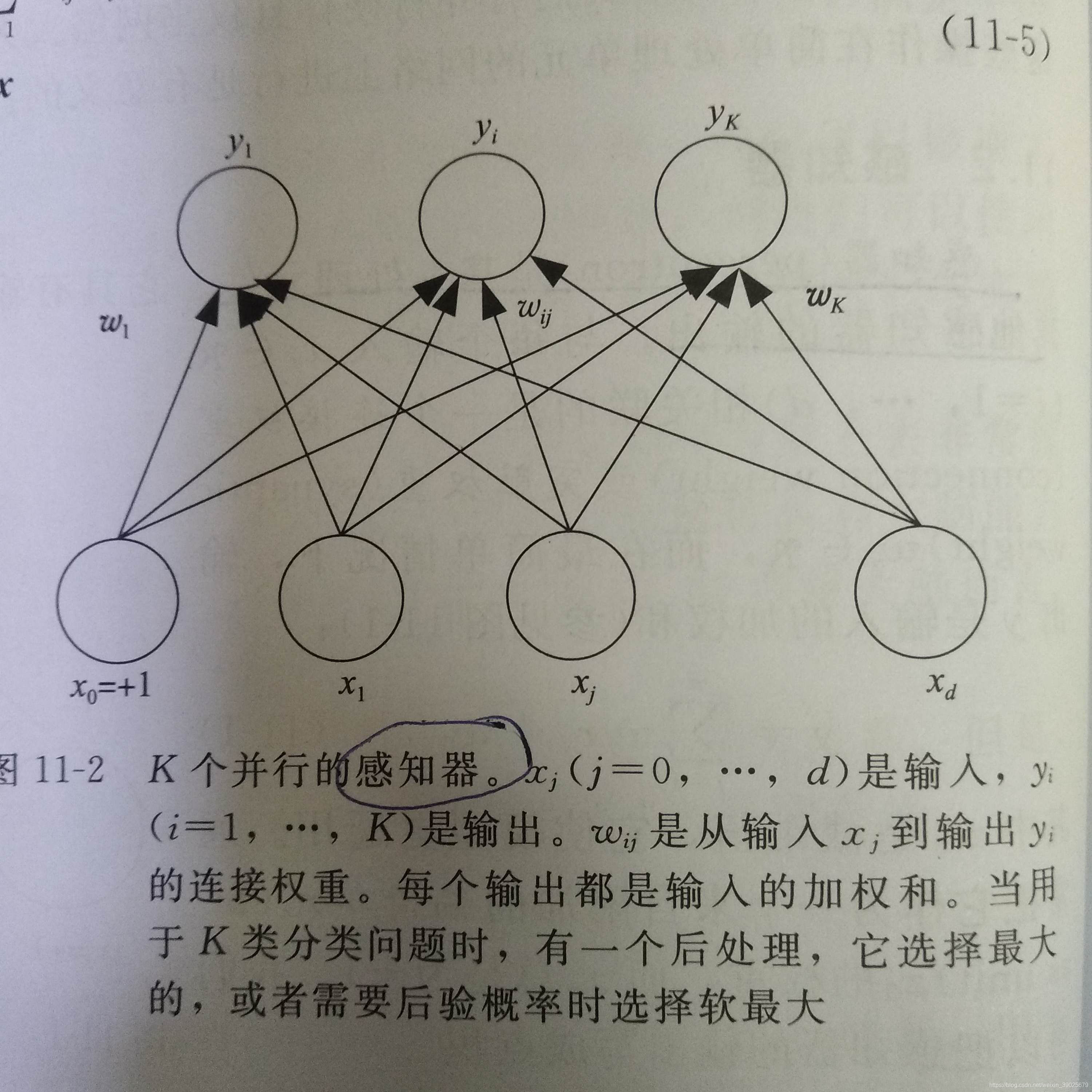
K个并行的感知机
![在这里插入图片描述]()
[ y 1 ⋮ y K ] = [ w 10 ⋯ w 1 d ⋮ ⋱ ⋮ w K 0 ⋯ w K d ] [ x 0 ⋮ x d ] \begin{bmatrix} y_1\\ \vdots\\ y_K \end{bmatrix} = \begin{bmatrix} w_{10}&\cdots&w_{1d}\\ \vdots&\ddots&\vdots\\ w_{K0}&\cdots&w_{Kd} \end{bmatrix} \begin{bmatrix} x_0 \\ \vdots\\ x_d \end{bmatrix} ⎣⎢⎡y1⋮yK⎦⎥⎤=⎣⎢⎡w10⋮wK0⋯⋱⋯w1d⋮wKd⎦⎥⎤⎣⎢⎡x0⋮xd⎦⎥⎤
因此权重矩阵W每一行代表输入到某一个感知机单元的权重
所以结论:
任何一个神经网络的输入在等式的最右侧,输出在等式的最左侧,权重在中间。
有时候感知机有阈值
θ
\theta
θ
定义
s
(
⋅
)
s(·)
s(⋅)为阈值函数,则
s
(
a
)
=
{
1
如
果
a
>
0
0
否
则
s(a)=\left\{ \begin{aligned} 1& &{如果a>0}\\ 0& &{否则} \end{aligned} \right.
s(a)={10如果a>0否则
a
=
y
a=y
a=y
即当输出
y
>
0
y>0
y>0即判给1类
为了计算风险,需要将输出转化为后验概率,使用
S
S
S函数
o
=
w
T
x
o=\textbf{w}^T\textbf{x}
o=wTx
y = s i g m o i d ( o ) = 1 1 + e ( − o ) y=sigmoid(o)=\frac{1}{1+e^{(-o)}} y=sigmoid(o)=1+e(−o)1
训练感知机
感知机定义了一个超平面,而神经网络感知机只不过是实现超平面的一种方法。
在线学习:逐个提供实例学习的方法
对于实例(x,r)误差表示:
E
(
w
∣
x
,
r
)
=
1
2
(
r
−
y
)
2
=
1
2
[
r
−
(
w
T
x
)
]
2
(1)
E(w|x,r)=\frac{1}{2}(r-y)^2=\frac{1}{2}[r-(w^Tx)]^2 \tag{1}
E(w∣x,r)=21(r−y)2=21[r−(wTx)]2(1)
r
r
r为真实值
y
y
y为输出值
若使用梯度下降法更新梯度,对w求导
∂
E
∂
w
=
Δ
w
=
−
η
(
r
−
w
T
x
)
x
\frac{\partial E}{\partial w}=\Delta w=-\eta(r-w^Tx)x
∂w∂E=Δw=−η(r−wTx)x
η
\eta
η:学习因子
权重更新公式
w
=
w
−
Δ
w
w=w-\Delta w
w=w−Δw
单个输出
y
=
s
i
g
m
o
i
d
(
w
T
x
)
y=sigmoid(w^Tx)
y=sigmoid(wTx)
互熵
E
(
w
∣
x
,
r
)
=
−
r
l
o
g
y
+
(
1
−
r
)
l
o
g
(
1
−
y
)
E(w|x,r)=-rlogy+(1-r)log(1-y)
E(w∣x,r)=−rlogy+(1−r)log(1−y)
多个输出
y
i
=
e
w
i
T
x
∑
k
e
w
k
T
x
y_i= \frac {e^{w_i^Tx}}{\sum \limits_ke^{w_k^Tx}}
yi=k∑ewkTxewiTx
互熵
E
(
w
i
∣
x
,
r
)
=
−
∑
i
r
i
l
o
g
y
i
E(w_i|x,r)=-\sum\limits_ir_ilogy_i
E(wi∣x,r)=−i∑rilogyi
调整参数的伟大公式:
- 更新=学习因子*(期望输出-实际输出)*输入
也就是说,更新的幅度正比于误差error,更新量还依赖于输入,对于学习因子过大,则更新过分依赖当前实例,就像系统只有短期记忆,如果因子太小,则收敛很慢。
学习布尔函数
学习AND布尔函数,一个感知机就可以解决,但是解决异或布尔函数,因此需要多层感知机
异或函数
| x1 | x2 | r |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
多层感知机
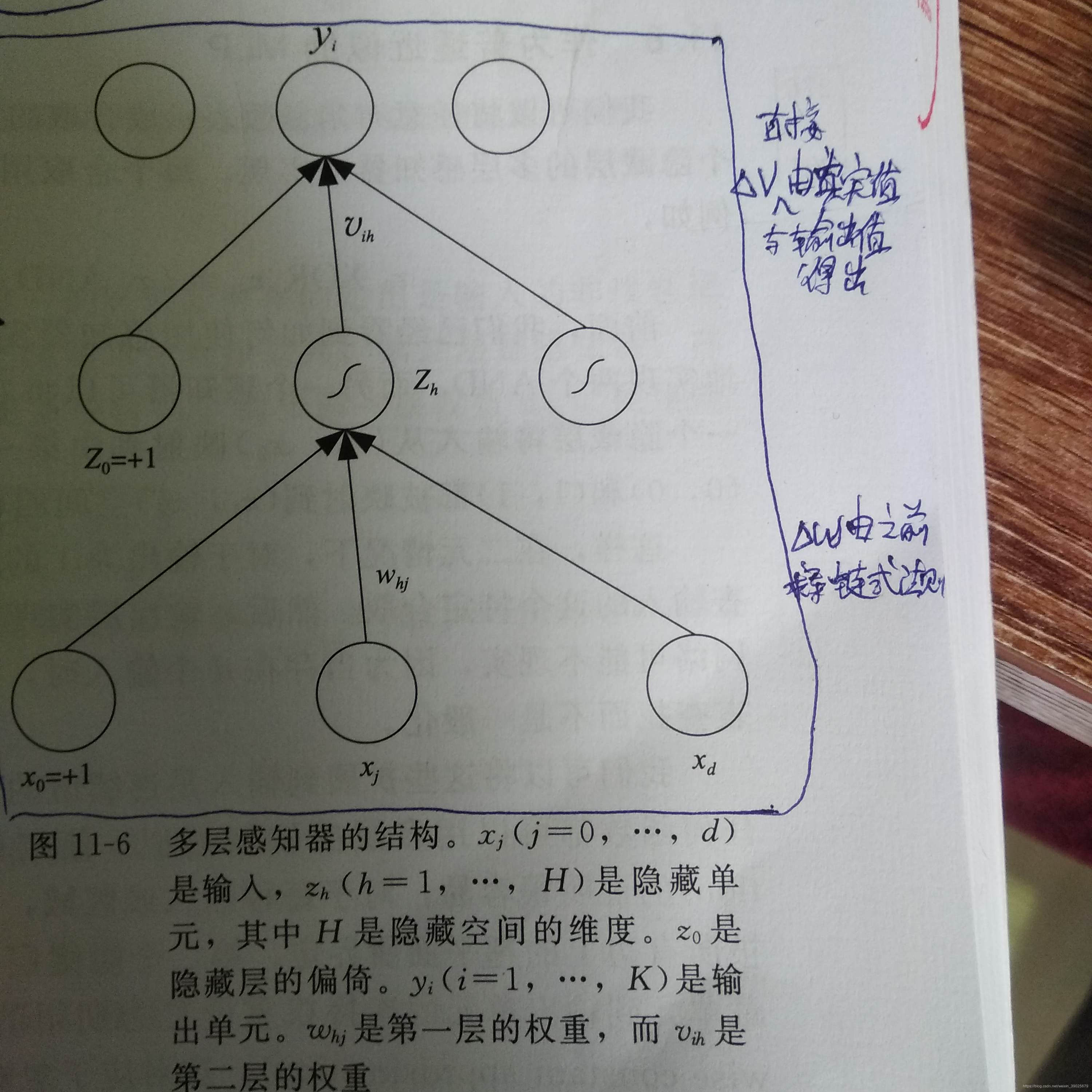
具有单层权重的感知机只能输入线性函数。
对于输入和输出加入层称为中间层或隐含层,即多层感知机。
Z
=
w
x
(2)
Z=wx\tag{2}
Z=wx(2)
y
=
v
Z
(3)
y=vZ\tag{3}
y=vZ(3)
向后传播算法(BP)
训练多层感知机和训练一个感知机一样。
由公式1,3对权重v求偏导
∂
E
∂
v
i
h
=
∂
E
∂
y
i
∂
y
i
v
i
h
=
−
(
r
i
−
y
i
)
Z
h
\frac{\partial E}{\partial v_{ih}}=\frac{\partial E}{\partial y_i}\frac{\partial y_i}{v_{ih}}=-(r_i-y_i)Z_h
∂vih∂E=∂yi∂Evih∂yi=−(ri−yi)Zh
- 假设去掉第一层,那么Z就为“输入层”,可以类比单层感知机公式
由误差公式1,公式2,3对 w h j w_{hj} whj求偏导( h h h第几个输入, j j j第几个输出)
∂
E
∂
w
h
j
=
∂
E
∂
y
i
∂
y
i
∂
Z
h
∂
Z
h
∂
w
h
j
=
−
(
r
i
−
y
i
)
v
i
h
x
j
\frac{\partial E}{\partial w_{hj}}=\frac{\partial E}{\partial y_i}\frac{\partial y_i}{\partial Z_h}\frac{\partial Z_h}{\partial w_{hj}}=-(r_i-y_i)v_{ih}x_j
∂whj∂E=∂yi∂E∂Zh∂yi∂whj∂Zh=−(ri−yi)vihxj
BP网络伪代码

非线性回归
两类判别式
多类判别式
多层隐含层
训练过程
改善收敛性
动量
自适应学习率
过分训练
构造网络
线索

 浙公网安备 33010602011771号
浙公网安备 33010602011771号