BUAA-OO-Unit1 Summary
第一次作业
代码设计
代码架构如下:
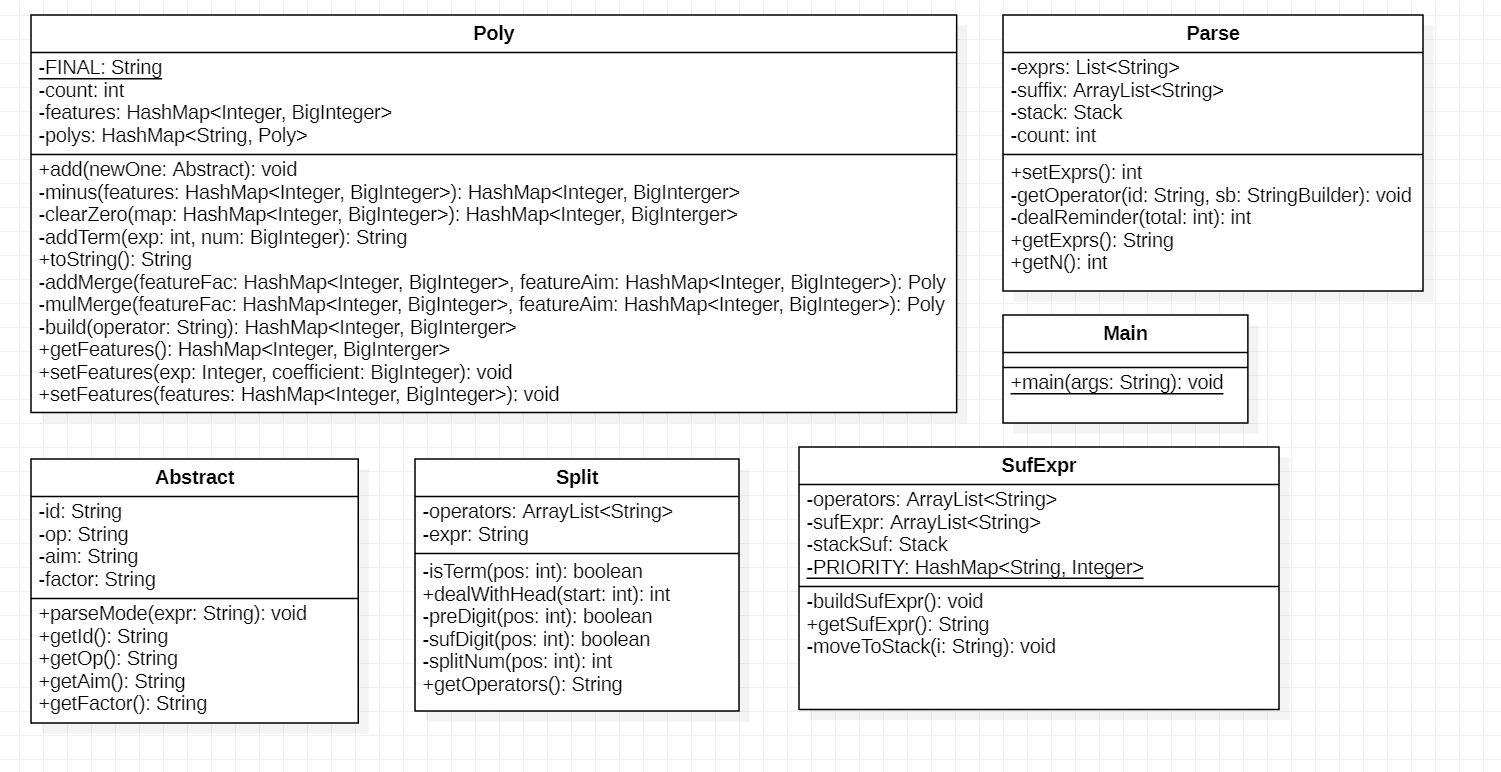
可以看到每个类没啥联系,就挺面向过程。
刚开始没啥思路,就打算先按预解析模式写,然后试一试能不能实现预解析的功能。
第一次的表达式比较简单,可以将表达式每一项拆解成系数和指数,可以设置一个HashMap存指数和系数的关系,设置一个HashMap存Id与多项式的关系,对于加减正常运算就好了,并判断下是否存在可合并的项。
然后就是比较重头的表达式解析了。
可以现将表达式的全部口号需要将一整串的表达式的有用信息一个个抠下来,并作一些小处理,小处理主要是辨别每一个正负号,本题中复杂的就是正负号的辨别,有些正负号意味着加减法,有些是因子前面的正负号,有些是项前面的正负号,每个这样的正负号优先级是不同的,这在处理成后缀表达式并得到最终结果时有很大的影响。(我是用栈来处理后缀的,符号的优先级对出栈顺序有很大影响,从而影响后缀表达式)
我的处理方法是将表达式开头(即第一个项前面可添加的\(\pm\))标记为+++ or ---,对于项前面的\(\pm\)(即第一个因子前可添加的\(\pm\))标记为++ 或--,并为其表明新的优先级。对于非加减法的\(\pm\),按照项开头、因子开头、带符号整数的顺序依次判断,例如+-1,会理解为+(-(1)),此时的整数因子为1. 转化为+++ -- 1,同理就算表达式开头为-1, 也是理解为--- 1, 而非-1 (感觉理解为-1应该也可以处理,但我为了对拍方便,和官方提供的转换程序一致就这么处理了)
而因为只有表达式的开头会有多一个符号,因此在每个表达式的开头,以及扫到(时进行一个检测
我的处理方法是将表达式开头(即第一个项前面可添加的\(\pm\))标记为+++ or ---,对于项前面的\(\pm\)(即第一个因子前可添加的\(\pm\))标记为++ 或--,并为其表明新的优先级。对于非加减法的\(\pm\),按照项开头、因子开头、带符号整数的顺序依次判断,例如+-1,会理解为+(-(1)),此时的整数因子为1. 转化为+++ -- 1,同理就算表达式开头为-1, 也是理解为--- 1, 而非-1 (感觉理解为-1应该也可以处理,但我为了对拍方便,和官方提供的转换程序一致就这么处理了)
将之前得到的拆解按照运算优先级配合堆栈就可以得到后缀表达式了,具体为如果遇到常数和x,就无条件出栈,放入后缀表达式的字符串中,遇到(就无条件入栈,遇到)就将栈里面的符号依次出栈,直到(出栈,其他符号,如果栈顶不是(或栈顶符号的优先级大于等于它那么就入栈,直到满足栈顶是(或优先级低于它,而对于优先级的判断,我是先打了一个表来判断。而对于上一个拆分得到的+++ 或者++,可以得到其优先级低于*,** ,高于+-(毕竟作用于项或者因子),其中++的优先级高于+++,上一个代码片段清楚一点
PRIORITY.put("**", 5);
PRIORITY.put("*", 4);
PRIORITY.put("++", 3);
PRIORITY.put("--", 3);
PRIORITY.put("+++", 2);
PRIORITY.put("---", 2);
PRIORITY.put("+", 1);
PRIORITY.put("-", 1);
PRIORITY.put("(", 0);
得到后缀表达式之后,事情变得简单了不少,对于后缀表达式来说,数字无条件入栈,遇到+,-,*,**就将栈顶的头两个元素A,B(B为栈顶)弹栈,并执行运算, A op B,得到的结果入栈,这边就是Id,如果是++,+++,--,---就将栈顶元素A弹出,得到op A后入栈
度量分析
对于Method来说
ev(G)(基本复杂度,Essential Complexity),用来衡量程序非结构化程度的,非结构成分降低了程序的质量,增加了代码的维护难度,使程序难于理解。基本复杂度高意味着非结构化程度高,难以模块化和维护。
iv(G)(模块设计复杂度(Module Design Complexity),用来衡量模块判定结构,即模块和其他模块的调用关系。模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。复杂度过高可能导致修正一个bug后会有新的bug
v(G)(圈复杂度,Cyclomatic Complexity)用来衡量一个模块判定结构的复杂程度,数量上表现为独立路径的条数,即合理的预防错误所需测试的最少路径条数,圈复杂度大说明程序代码可能质量低且难于测试和维护。
经验表明,程序的可能错误和高的圈复杂度有着很大关系。
对于Class,有OCavg和WMC两个项目,分别代表类的方法的平均循环复杂度和总循环复杂度。
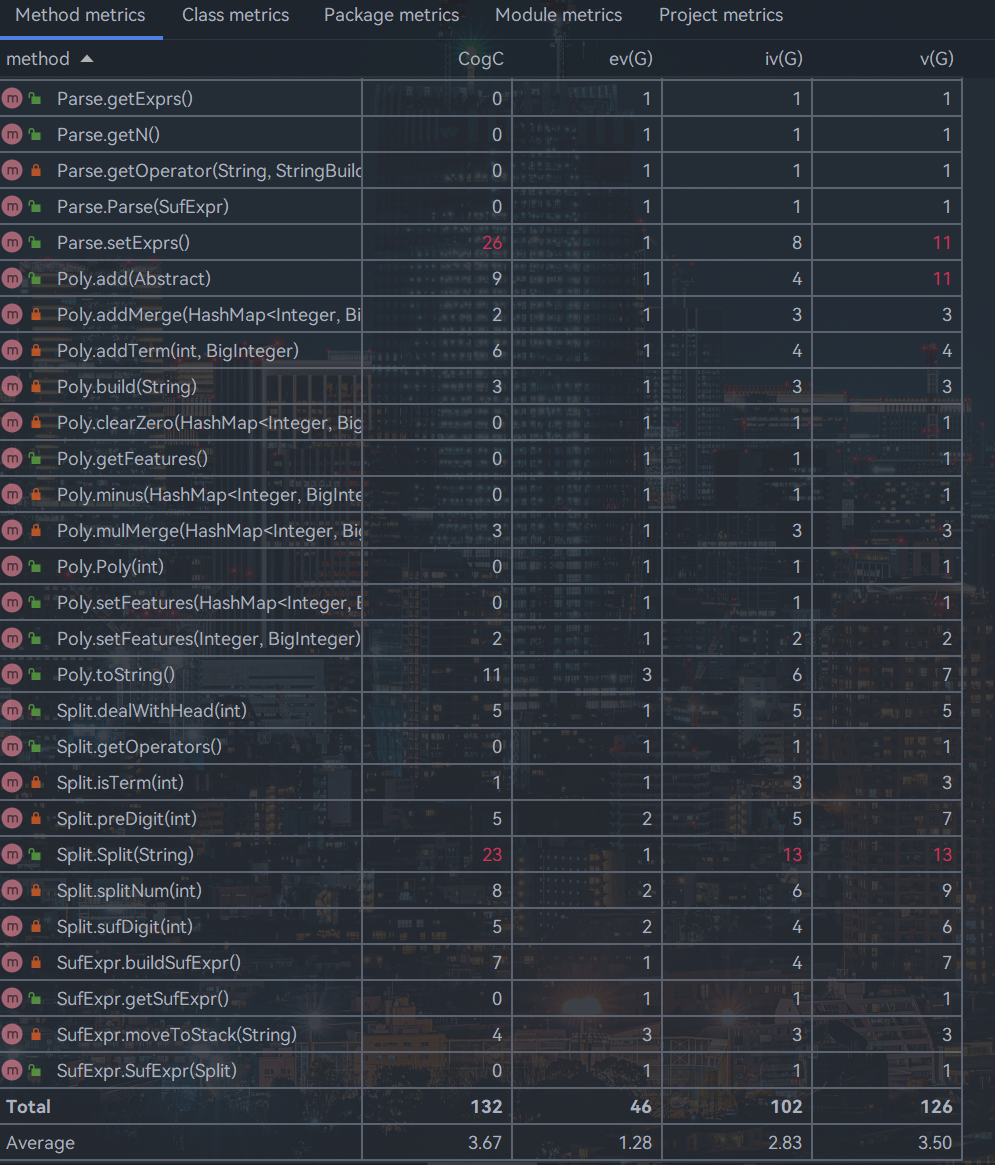
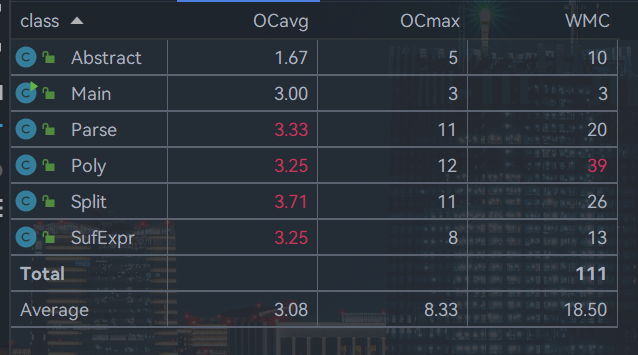
可以看到复杂度和耦合度都不低,因为当初还没有彻底摆脱面向过程,每个类都不是那么独立
bug 分析
本次作业强测和互测没有出现bug,自己造了一个随机数据生成和评测机。在互测阶段也是依靠对拍程序找到了别人的bug,分别是常数处理不规范,和0次幂处理不规范。
第二次作业
代码设计
代码架构如下:
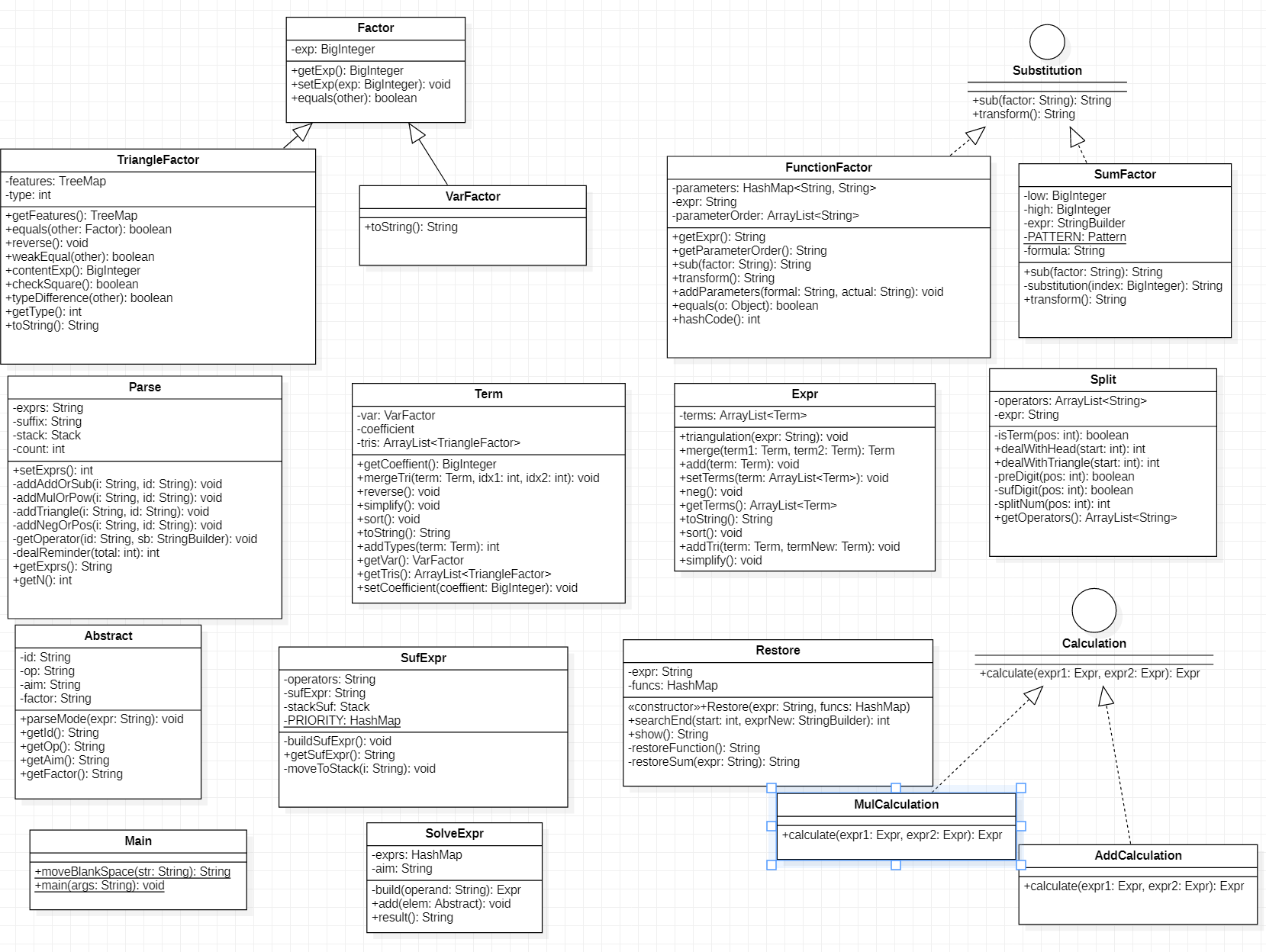
可以看到架构明显复杂栏很多,也是有了点层次关系出来了。也增加了很多类。
新增了自定义函数,求和函数和三角函数。对于自定义函数和求和函数中,侧重点在函数的拆解。这次我也是用官方的解析程序试了很久,感觉好像可以把字符串替换并加外层括号保证整体性,然后按优先级取出来继续调用作业一点架构。加上后缀表达式是不怕多层嵌套括号的,所以就选择了这样的字符串替代的方法,然后注意一些小细节的处理,比如求和的时候,要把sin当中的i排除掉这种的。
三角函数是在表达式运算方面的,这个也是在这次作业中困扰我比较久的一个方面。也是对这个解决方法的思考中,慢慢有了一些面向对象思想的萌芽的吧(现在回想起来方式还笨拙的)。我开始去用层次化的方法给表达式建模。表达式就是一个个项相加,我将每一个项概括为 系数 * 三角函数因子列表 * 幂函数, 每个三角函数和幂函数都带着指数。对于不带三角函数的项,我当初为了保持形式的一致性,就选择用cos(0)占位。(所以刚开始的我形式贼长,每个项都是cos(0)的n次方再乘上一些东西)在实现的过程中,被浅复制深复制搞得很难受,刚开始并不会不可变对象或者序列化这种操作,就是new一个新的对象,再一层层把原来的东西转移过来。对于运算,也是通过实现了接口,比较有逻辑性一点。
再通过中测之后开始了性能分的磨练。再处理cos(0)的过程中也是慢慢发现了其实确实没必要对每一项都弄一个cos(0),然后也再猜测下一次可能扩展的方向,也做了一些准备。后面处理了三角函数平方和的。因为要保证除了一个平方项不同,其余都相同,我的方法将每个一个项的三角函数因子强制分一个顺序,我的分法是先比指数,指数一样,sin放在cos前面,都是sin(或cos)比里面的指数,这样的,然后对于平方项,将平方全扔到最后面(这样就比对的时候,如果比到了平方就说明之前都是一样的),然后将剩下的平方项暴力比对,要保证每个项要不出现,要不对应的三角函数出现(只能有一次)。然后对于 \(a * cos^2(x) + b * sin^2(x)\),就比较a、b的大小,做部分化简也就好了。
度量分析
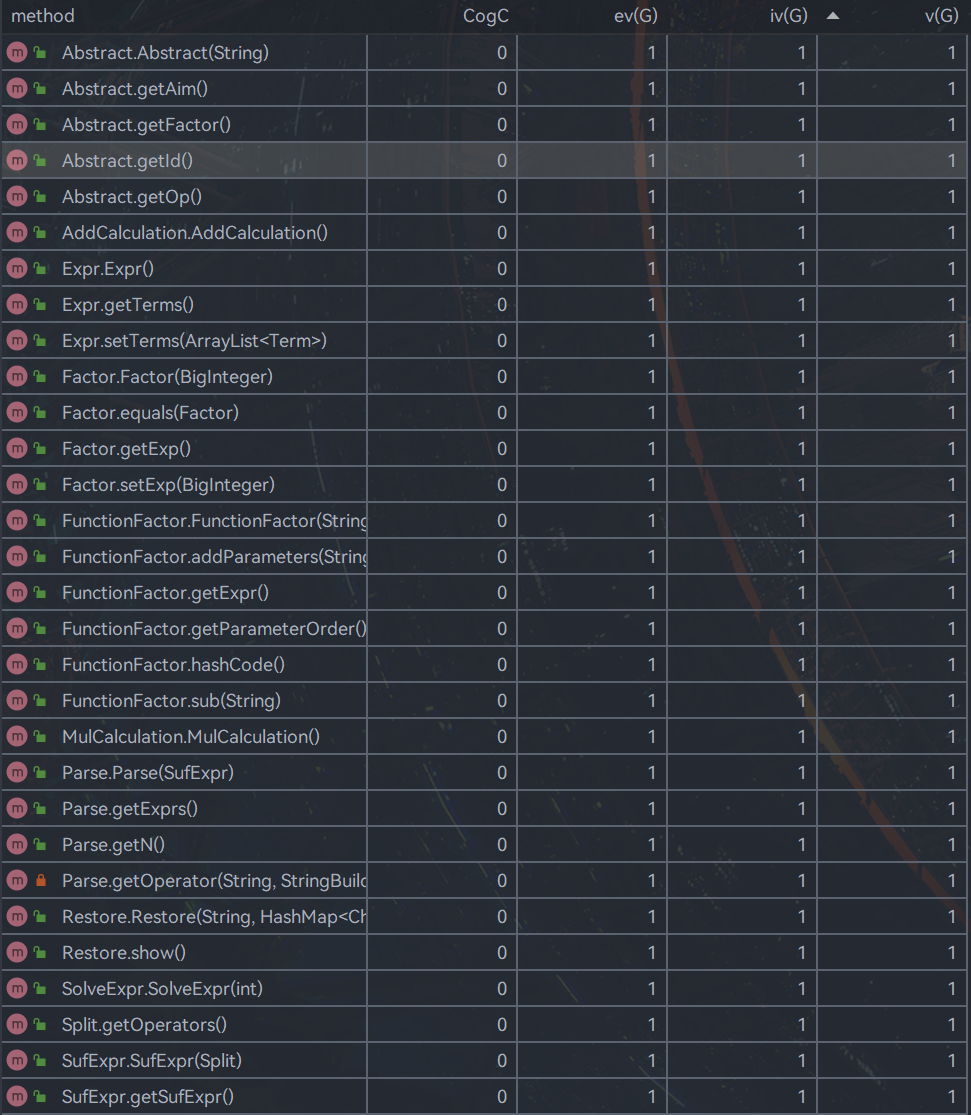
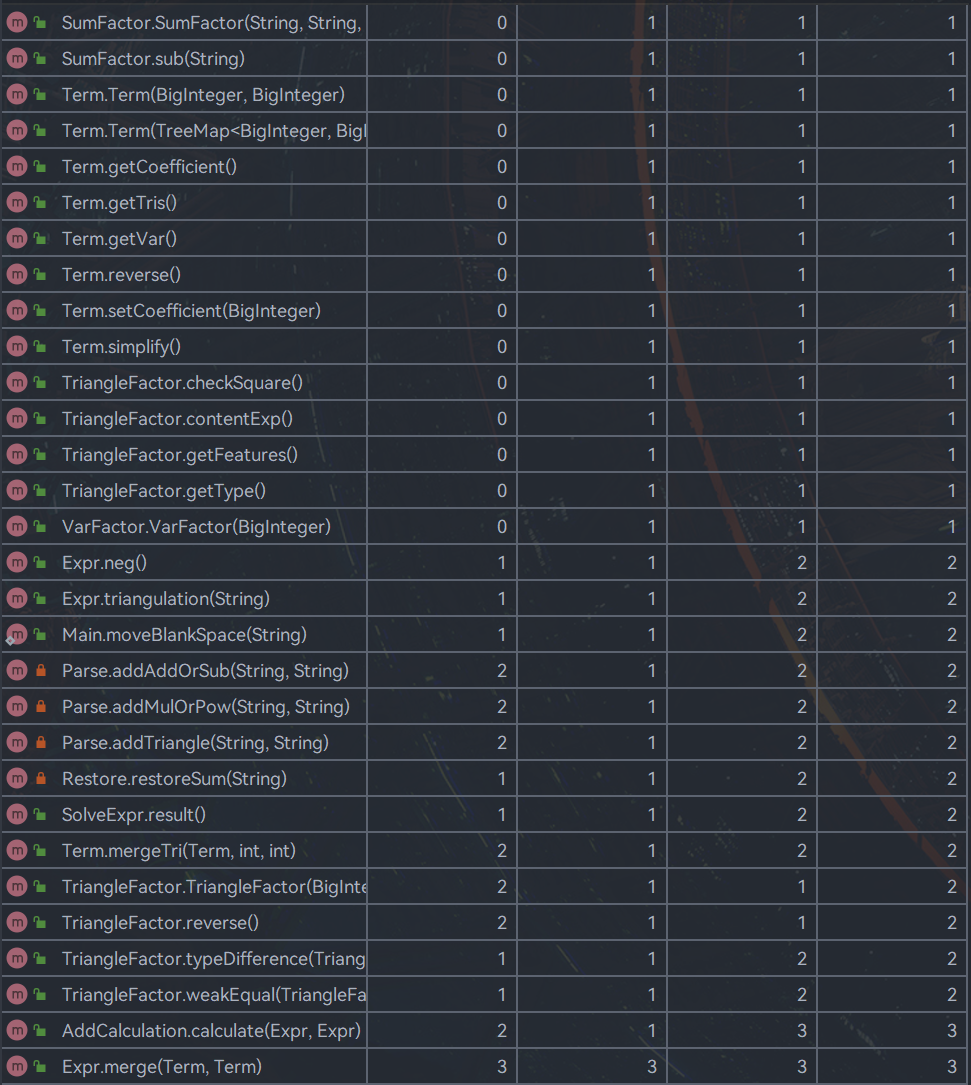
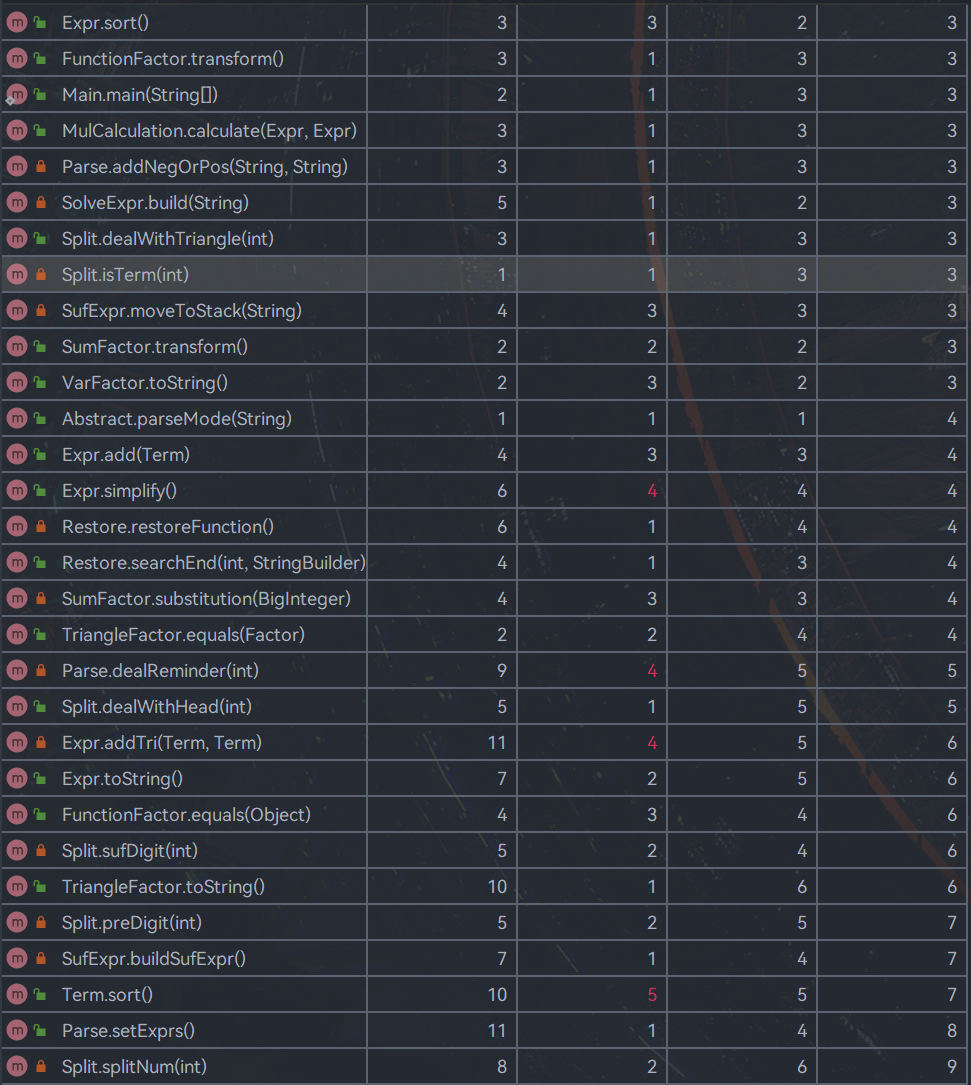
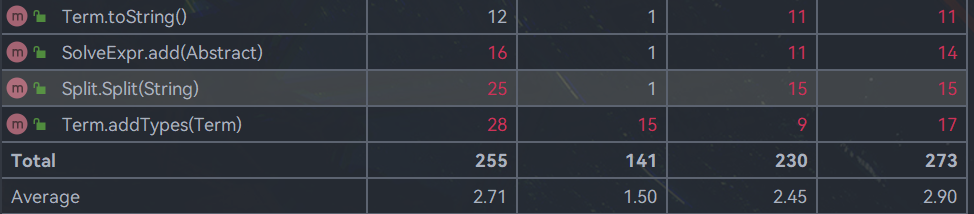
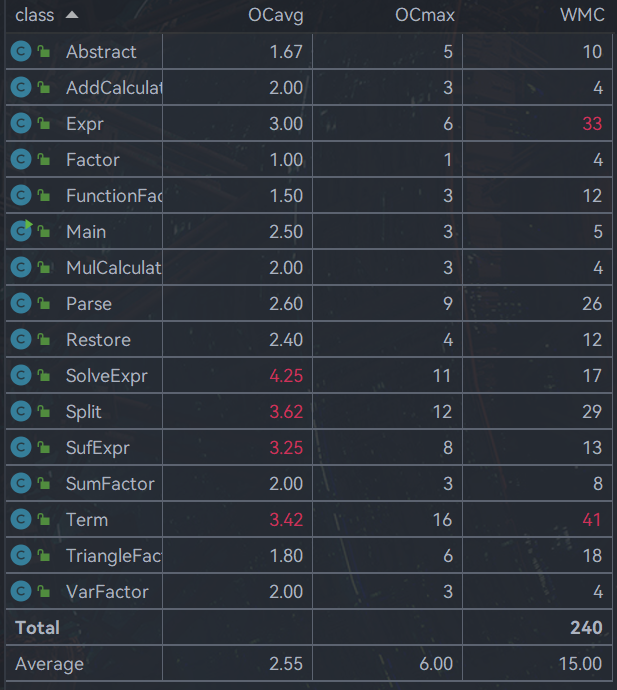
因为拆解了类的功能,所以大多数类的复杂度和耦合度控制的都还行,但是还是在解析表达式的有关类不太好,这也确实是想调整的一个地方。还有就是addtype,那个类的构造确实不够清晰,是最后为了实现三角平方和的实现,这个方法的面向过程痕迹蛮重的
bug分析
本次强测和互测没有被发现bug,因为这次对数据限制多了,也更加复杂了,并不会写对拍程序。最后的测试方法,就是想着这是别人的代码,我会怎么给这个代码测试。在互测时因为没有评测机了,就开始读代码了。发现了有关化简时,用字符串的方法特判断一次方的问题。他直接将**1给剔除,因此在x**10这个数据中出现了问题。
第三次作业
代码设计
代码架构如下:
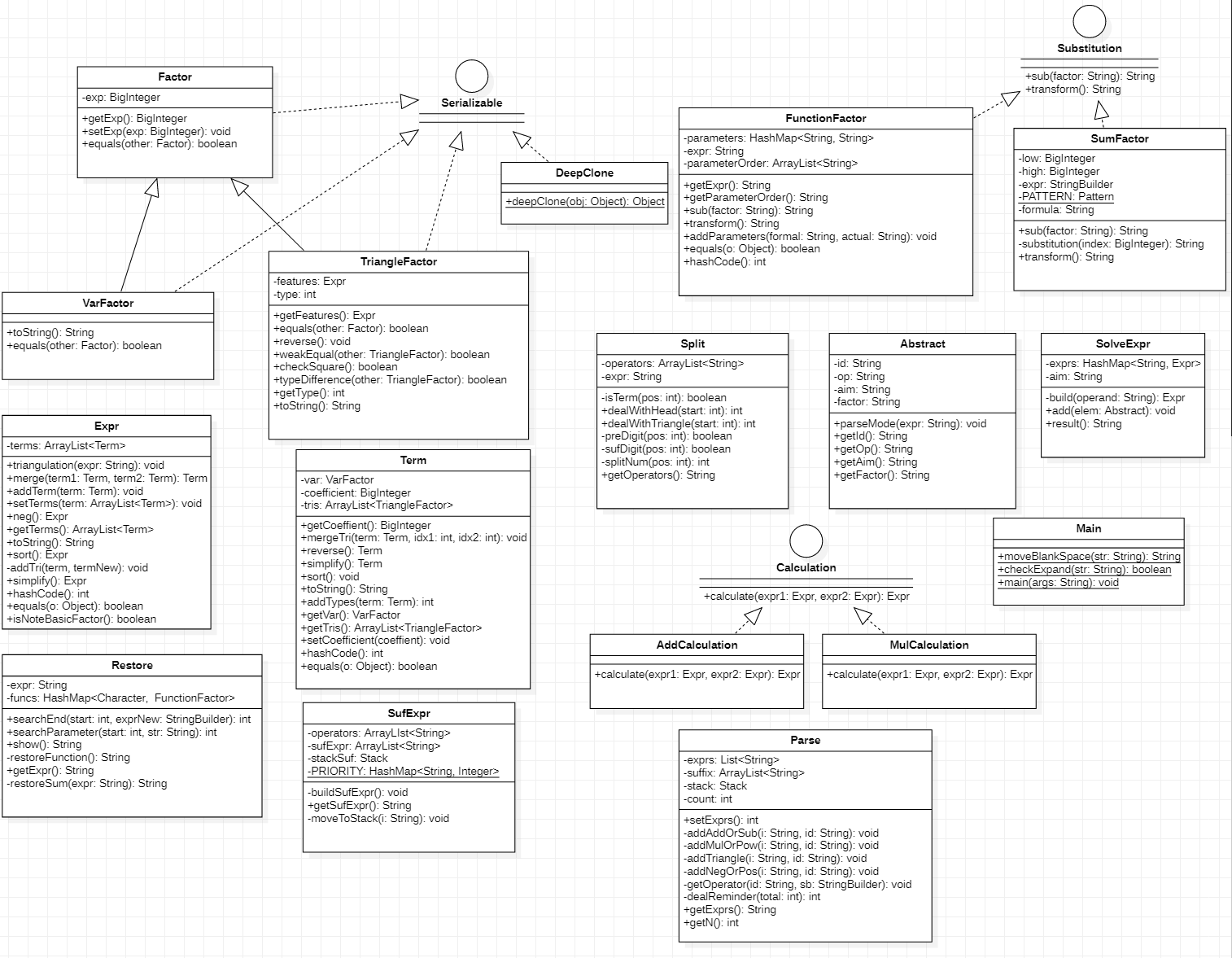
和第二次没啥太大的差别了,因为考虑了第三次可能会出现的扩展情况,因此需要调整的地方不多。一个是不让每个项都强制带一个cos(0)了,,确实没有太大的必要。还有因为上次吃了深复制浅复制的亏,这次将需要复制的项实现了序列化。后面也觉得直接对原对象进行修改确实风险不少,很有可能会有些不知名bug,就学习BigInteger那样,每个操作都返回一个新的对象。然后这些工作做完后,上次的耦合度高的地方就没有时间做进一步修改了😢
说一些要注意的点。一个是判断三角函数表达式要不要加括号,我的思路是不需要加括号的表达式无非就整数(无三角函数,幂函数指数为0),幂函数(系数为1,无三角函数),一个三角函数(系数为1,无幂函数)特殊判断一下。还有就是三角排序的时候以前直接看里面的幂函数因子的指数就完了,但现在里面是一个表达式了,我们仍可以认为的规定表达式的顺序,我是按照先指数幂函数指数,三角函数个数,三角函数指数,三角类型,三角函数包含的表达式,系数的顺序,遇到三角函数包含的表达式就递归调用就完了。
度量分析
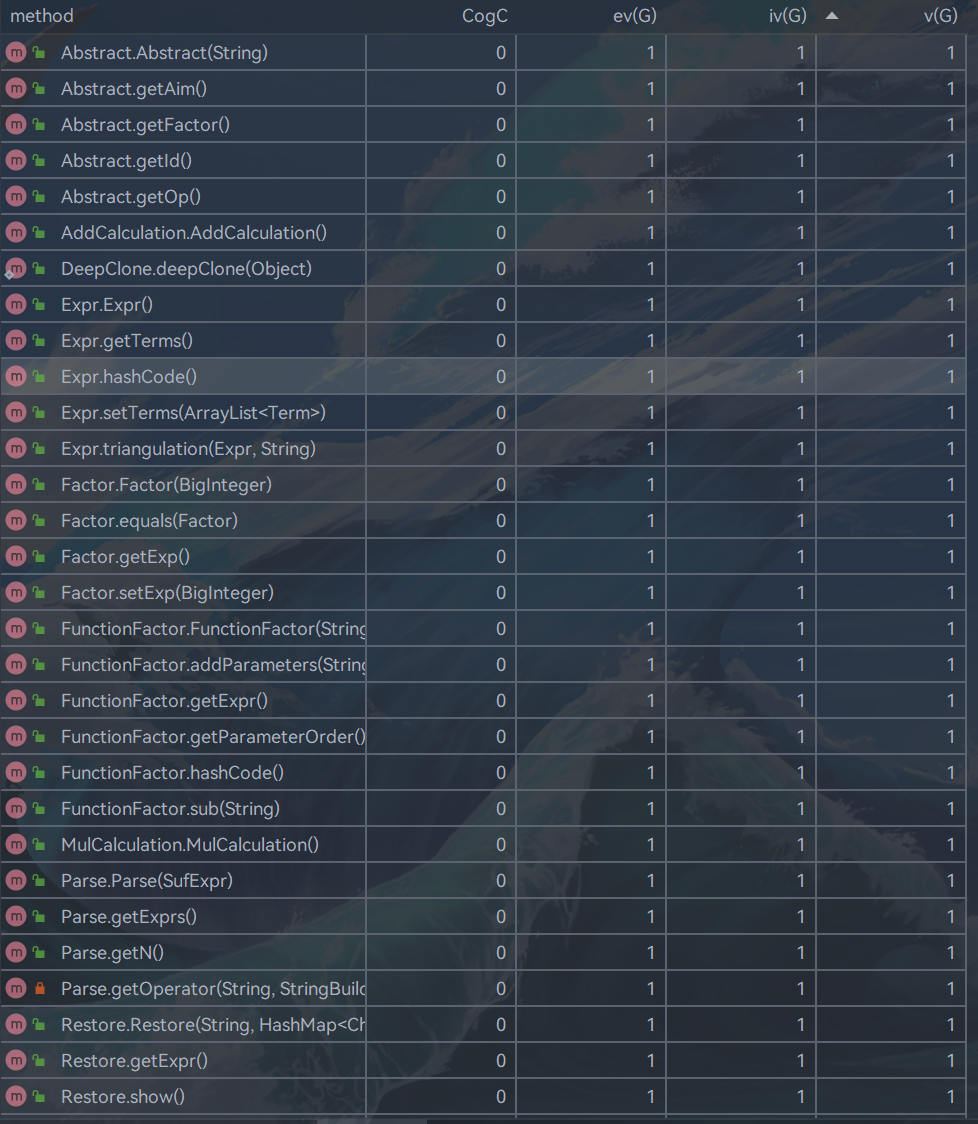
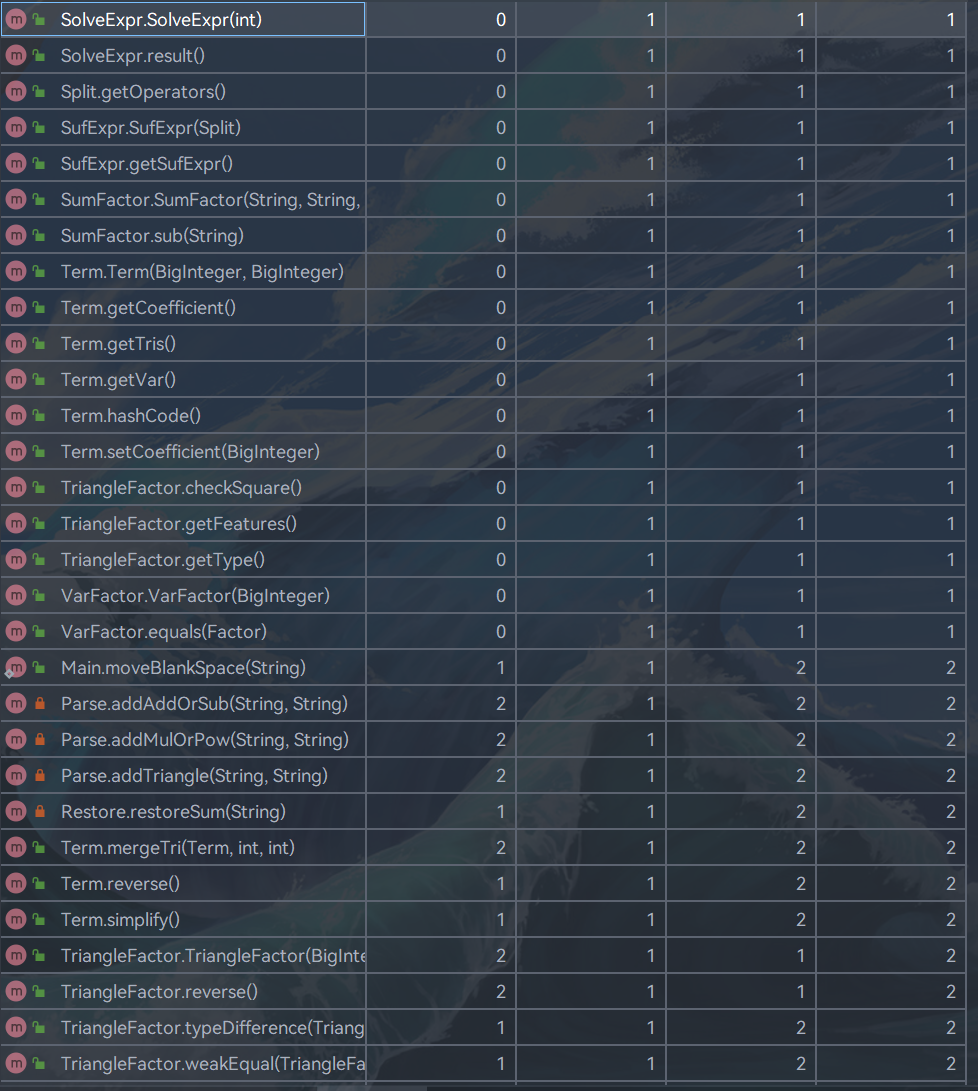
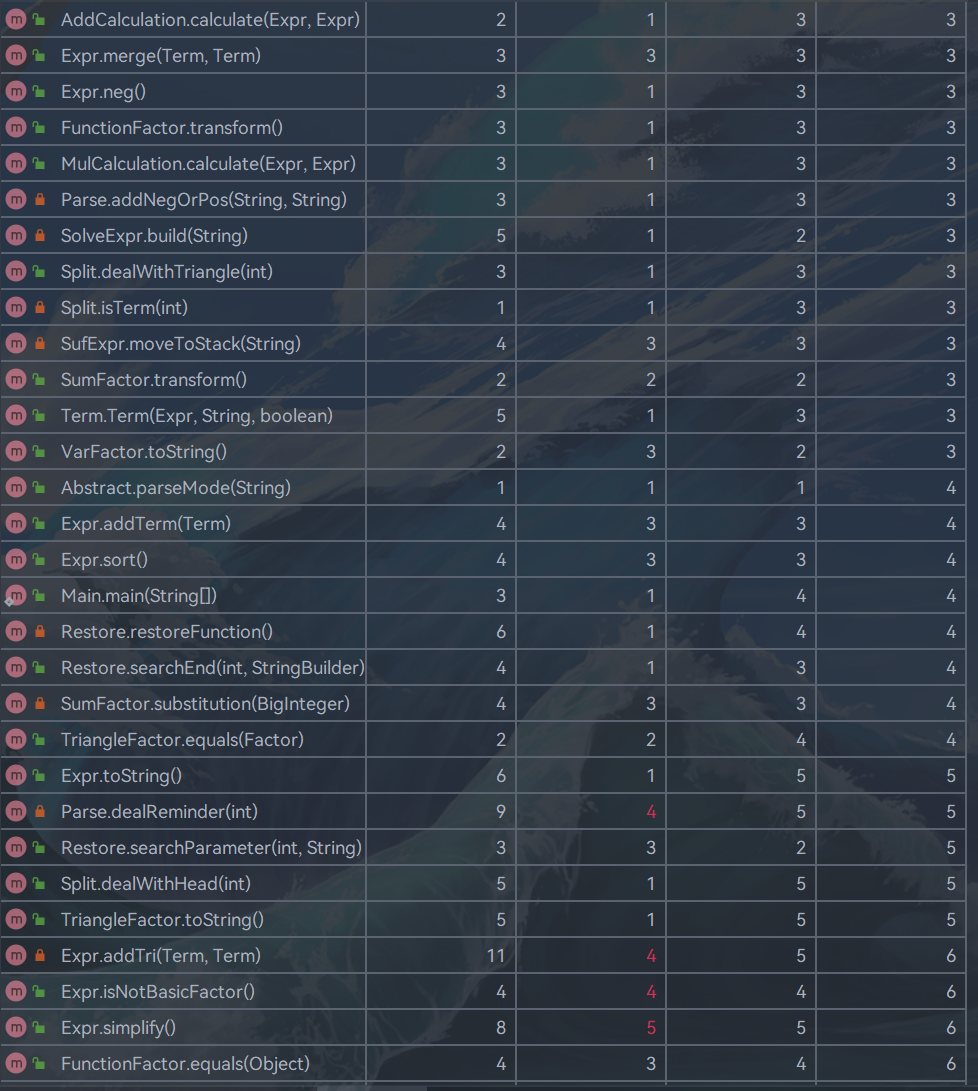
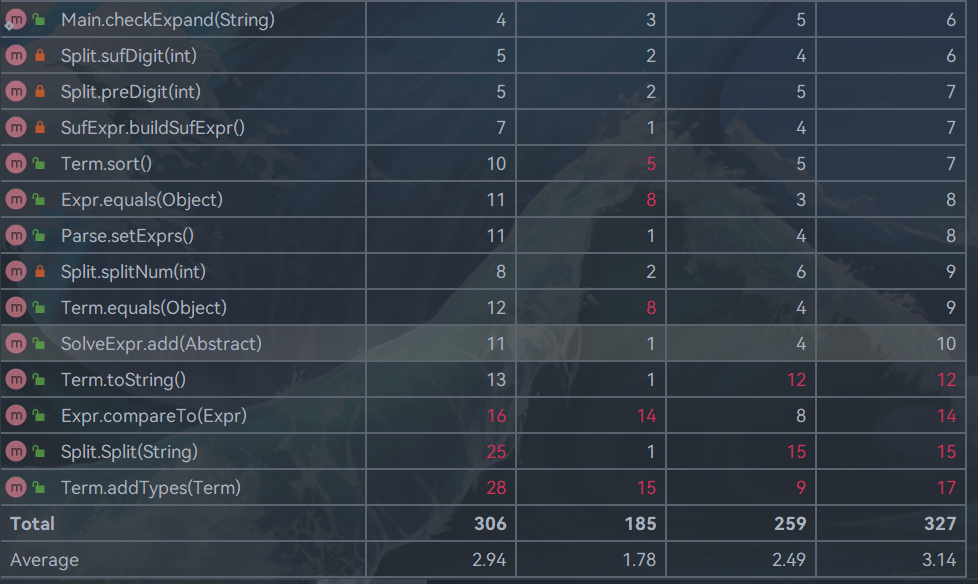
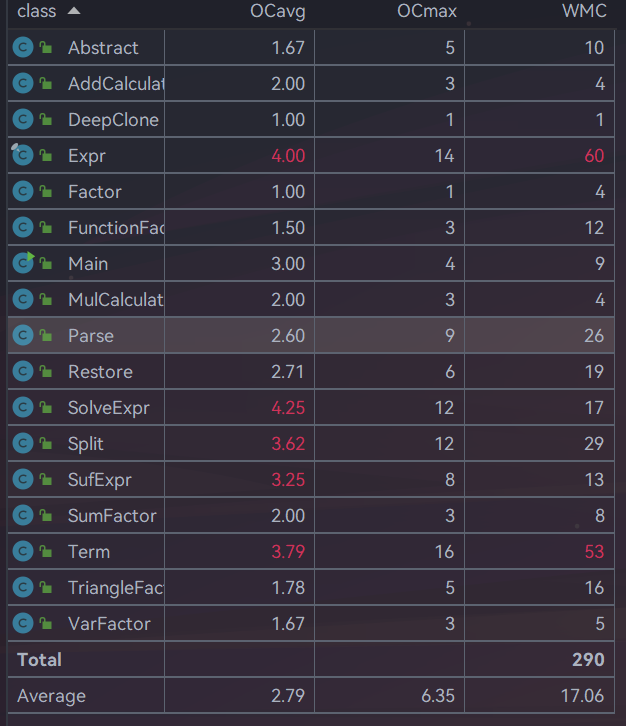
复杂度的耦合度高的主要还是表达式预解析和表达式类和项类。这个两个类某些方法的架构确实不太优秀,会出现相互调用的情况,导致了这个问题。
bug分析
强测没问题,但互测出现了一个bug。问题在于我项的equal方法判断失误,我忘记先判断每个项的三角函数个数是否相等。导致如果一个有三角函数,一个没有,其余相等,会有可能个出现bug,互测也被揪出来了。自己调试的时候只测了一些边界而没有注重一些细节的实现,这也是今后要注意的。找别人的bug发现**1仍然有人犯错,还有就是有同学三角函数有将-号提取出来,但是做平方时并没有将其运算,导致结果多了一个-号。还有就是经水群大佬提醒从而发现sum的上下限可以达到BigInteger.
感受
这次作业的过程中,感受到了自己的成长。从刚开始只会机械的构造一些其实完全可以通过函数实现的类,到后面慢慢能感受到面向对象带来的多态的优异性,对java语言也有了更多的了解。感谢课程组的老师、助教,讨论区的大佬和帮助我的同学,让我第一单元没有那么痛苦吧哈哈哈哈哈。下一单元加油!
一切皆为对象




 浙公网安备 33010602011771号
浙公网安备 33010602011771号