mooc 数据结构 （浙江大学） 学习笔记

第一章 基本概念

2020-11-16

1.三目运算符　　

条件运算符由两个符号组成"?"和":", 要求有3个操作对象,所以也叫它三目运算符。是右结合的，也就是先将最右边的? :划分成一个表达式，然后将其当作一个操作数，从右至左依次类似的划分剩下的? :.eg: x>0?1:x<0?-1:0==  x>0?1:(x<0?-1:0)

　　

它的一般形式为:

　　　　　　　　表达式1?表达式2:表达式3;

如果表达式1为真,则取表达式2值,否则取表达式3值.

eg:　　　

　　if(a<b)
   　　 min=a;
　　else
   　　 min=b;

　　可以用下面的条件运算符来处理

　　min=(a<b)?a:b; 相当于：如果a<b为真,则表达式取a值,否则取b值.

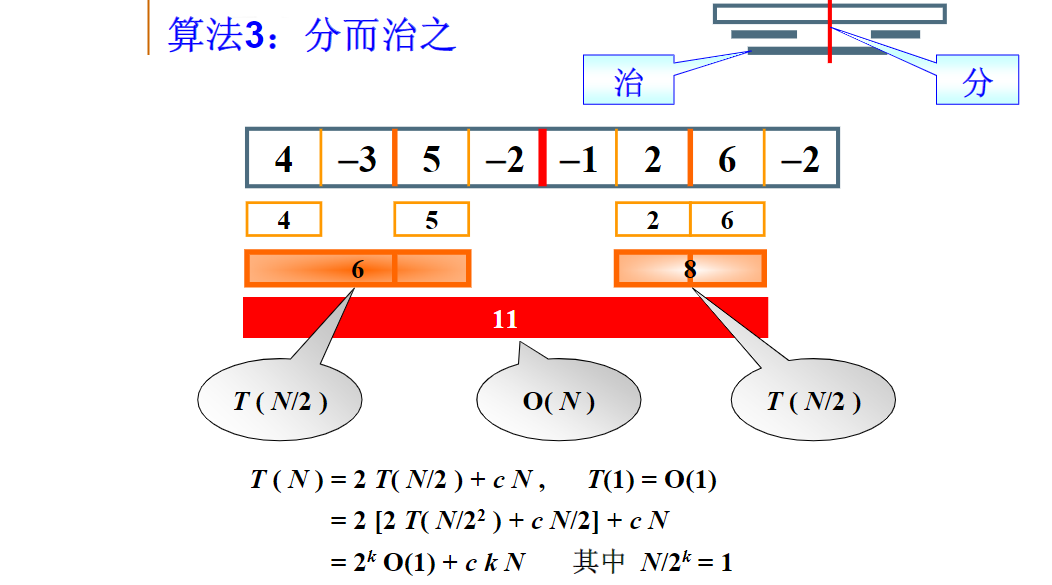
2.算法“分而治之”

 

#include <stdio.h>

int max3(int A,int B,int C)
{
    /*返回3个整数中的最大值*/
    return A>B?A>C?A:A>C?
    
}
int divideAndConquer(int List[],int left,int right)
{
    /*分而治之求list[left]到list[right]的最大子列和*/
    int MaxLeftsum,MaxRightSum /*存放左右子问题的解*/
    int MaxLeftBorderSum,MaxRightBorderSum;/*存放左右跨分界线的结果*/
    int LeftBorderSum.RightBorderSum;
    int center.i;
    if(left == right)/*递归条件终止，子列只有1个数字*/
    {
      if(List[left]>0)
            return List[left];
        else
            return 0;
      
    }   
    /*分*/
    center = (left+right)/2 /*找中分点*/
     /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
     /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */

    
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */

    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}

int MaxSubseqSum3( int List[], int N )
{ 
    return DivideAndConquer( List, 0, N-1 );
}
    return 0;
}

 

3.while 循环

只要给定的条件为真，while 循环语句会重复执行一个目标语句。

while(condition)
{
   statement(s);
}

4.二分法（排序）

 

#include <stdio.h>
int divideAndConquer(int List[],int left,int right)
{
    /*二分后，分别把list[left]和list[right]进行从大到小的排序*/
    int  MaxLeft[center],MaxRight[center]; /*存放左右子数组*/
    int center,i,j,s;
    if(left == right)/*递归条件终止，子列只有1个数字*/
    {
            return List[left];
      
    }  
     /* 具体的排序过程 :把s当作标准,i从左边开始，j从右边开始，遍历到i,j相遇，顺序很重要！！！必须从右往左遍历！！if list[j] <s,j停止，i继续，直到遇到list[i]>s，交换i、j，
    
        最后在列表左边的数一定都小于s，右边的数都大，最后再交换基准数*/
    /*基准数*/
    s=List[left];
    i=left+1,j=right;
    while(i!=j)
    {
        /*s顺序必须是先从右往左*/
        while(list[j]<s&&i<j)
            j--;
        while(list[i]>s&&i<j)
            i++;
        /*在i,j没相遇前交换*/
        if(i<j)
        {
            m=list[i];
            list[i]=list[j];
            list[j]=list[i]
            
        }
            
    }
    center=i
    /*交换基准数*/
    a[left]=a[i];
    a[i]=s;
    
     /* 递归继续求左右两边 */
    MaxLeft[center] = DivideAndConquer( List, left, center);
    MaxRight[center] = DivideAndConquer( List,center+1,right);
    
        
        
        
    

int MaxSubseqSum3( int List[], int N )
{ 
    return DivideAndConquer( List, 0, N-1 );
}
    return 0;
}