计数DP

计数DP

DP一般最大/最小/方案，这里求的即方案(个数)

整数划分
选出的数(不考虑顺序)恰好等于n的情况

多种考虑方式，不同的转移方程

(一)背包思路
将n看作n容量背包，存在n个物品体积(1，2···n)，类完全背包思想，考虑恰好装满背包的方案有多少

划分方式 <=> 完全背包选法

此时即可通过完全背包思考方式推出本题的状态转移方程：最大价值变为符合数量(方案数)

(优化)关注f[i][j]的由来:

f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - i * 2] + ... + f[i - 1][j - i * s];//总和=每一个方案的和
又有：
f[i][j - i] =           f[i - 1][j - i] + f[i - 1][j - i * 2] + ... + f[i - 1][j - i * s];
则推出
f[i][j] = f[i - 1][j] + f[i - 1][j - i]；

同完全背包可将1维优化，则有：f[j] = f[j] + f[j - 1];

点击查看代码

f[0] = 1;
for (int i = 1; i <= n; i ++ )
    for (int j = i; j <= n; j ++ )
        f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;

(二)其他思路
对于总和i，考虑恰好分成j个数的和的方案数

状态划分：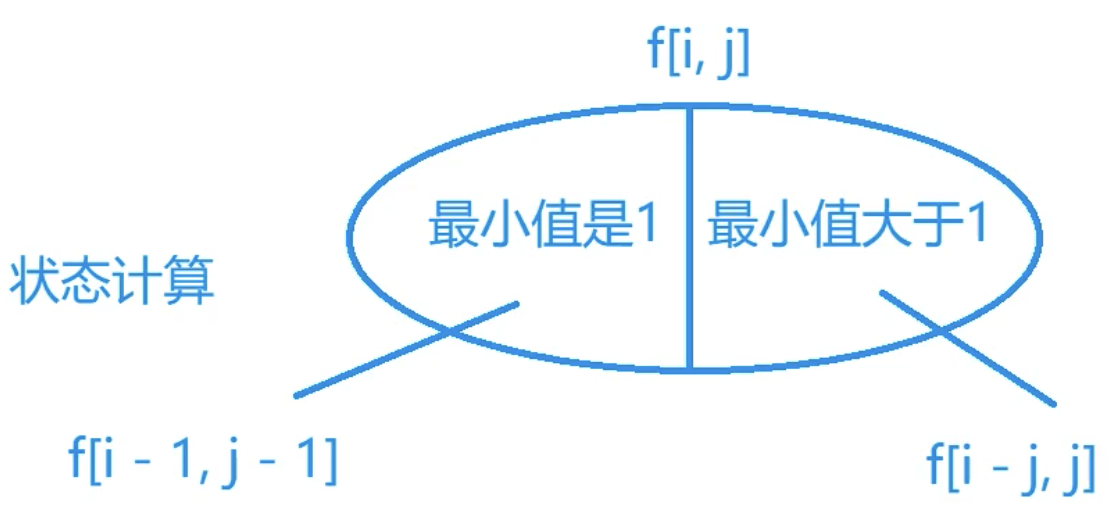
根据最小值是否为1划分：

• 最小值是1： 其中每个方案都存在1，同时去掉1(总方案数不改变)变为：总和i-1，恰好是j-1个数和的方案：f[i - 1， j - 1]

全+1即f[i，j]，方案数相等

• 最小值不是1：(同理)由于每个方案最小值都大于1，将方案中每个数拿出1，则变为：f[i - j, j] (总和拿出了j，由于拿出j此时仍恰好为j个正整数和)

此时每个方案中每个数+1，则为f[i，j]

状态转移方程：f[i，j] = f[i - 1][j - 1] + f[i - 1][j];
此时对于答案要进行枚举：ans = 分1个数和f(n，1)+分2个数和f(n，2)+···+f(n，n)

即求和才为答案

点击查看代码

f[1][1] = 1;
for (int i = 2; i <= n; i ++ )
    for (int j = 1; j <= i; j ++ )
        f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
//答案求和
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;