状压DP：采用二进制集合表示法压缩方案

很有特点，一般20就很极限(2^20大概1e6)，当n<=20则可以看是否状态压缩

状压D：通过二进制下0/1表示情况

不关心之前走了哪些，对于我来说是一样的

常见是用二进制数0/1进行压缩状态
前置知识位运算符：(如：<<，>>，|，&，^等)

二进制集合表示法(重要)：状压Dp的方案情况即采用的是二进制集合表示法

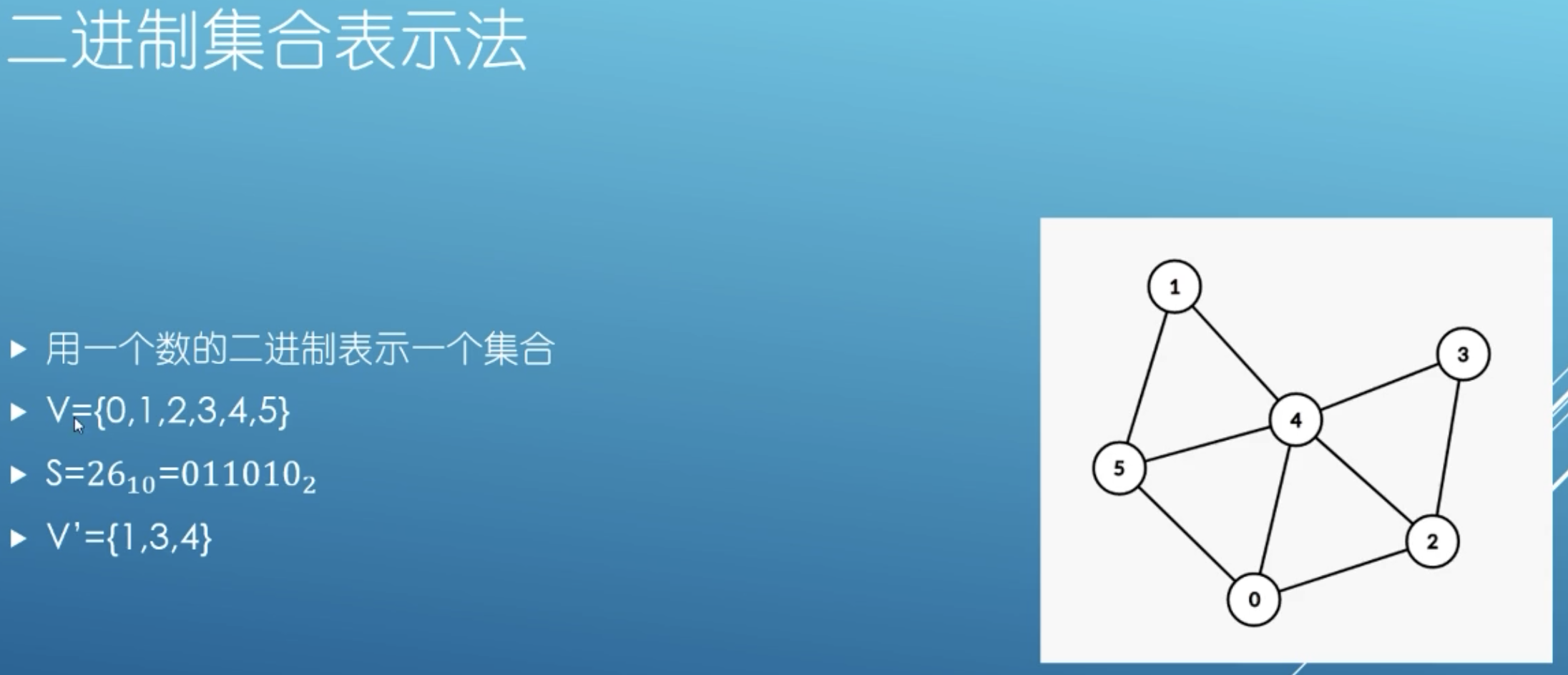
数s二进制状态下0/1代表节点i是否在s所表示集合v‘中

对于集合v和状态s来说总可以得到s所表示集合v‘

TSP问题：找权值最小哈密顿回路
状态表示： dp[i][s]表示当前在i节点，已经访问过节点集合为s，所经过路径的最小权值和

e.g.dp[1][\(26_{10}\)] = dp[1][ \(011010_{2}\)]，当前在1节点，且走过1，3，4节点

DP尽量记录有效信息旨在减少状态数量

TSP问题中只关心经过哪些点和当前在哪个点，及路径权值和，具体走的路径不用记录(对后续状态有相同影响)

转移方程： dp[j][s｜(1 << j)] = min(dp[i][s] + G[i][j]);

s | (1<<j) 表示将s二进制位j置1操作，即将j加入s集合中 = 当前在节点i，走过节点集合为s

这里从0开始，若从1开始则为：1<< j - 1(避免二进制位浪费0(1位))

初始状态：dp[i][1 << i] = 0;当前在i节点，且只经过i节点权值和

状压DP的枚举方式：采用子集枚举

不同于其他，状压DP采用枚举子集的处理方式

确定顺序：对于TSP问题应符合的顺序是：保证s｜(1 << j)集合要在状态s之后枚举(以此可知顺序正确)
对于s | (1 << j)一定有为s状态加上某一值，顺序枚举即可

范围：下界0～上界(1<<n) - 1(对于1<<n落在n+1位，此时-1则有上界全1)
(子集枚举也保证了集合的all子集一定是处理好的)

1.用确定状态更新其他状态：//在i下一步走j

点击查看代码

for(int s = 0; s < (1 << n); ++ s) {
    for(int i = 0; i < n; ++ i) {
        if(s & (1 << i)) {//在i节点则i必须在s集合
            for(int j = 0; j < n; ++ j) {//下一步为j
                if(!(s & (1 << j)) && G[i][j]) {//去j，那么j一定不在s，且ij间存在边
                    dp[j][s | (1 << i)] = min(dp[j][s | (1 << i)],
                                        dp[i][s] + G[i][j]);
                }
            }
        }
    }
}

若s没经过当前节点i则一定不合法
其中判读ij是否有边，也可根据G[i][j]!=INF判断

2.知道当前状态枚举all之前状态，来更新当前状态：在i，上一步走的是j

点击查看代码

for(int s = 0; s < (1 << n); ++ s) {
    for(int i = 0; i < n; ++ i) {
        if(s & (1 << i)) {
            for(int j = 0; j < n; ++ j) {//枚举之前的j
                if((s & (1 << j)) && G[j][i]) {//s集合中必须有j，我枚举我之前，通过j走到当前i
                    dp[i][s] = min(dp[i][s],
                               dp[j][s ^ (1 << j)] + G[j][i]);//当前在i，则s必然有i，但我未转移i，去掉
                }
            }
        }
    }
}

poj3311 Hie with the Pie

蒙德里安的梦想 P10975 Mondriaan's Dream
考虑放入小方格情况，发现当横向小方格摆放完成：有纵向小方格的摆方方式固定(顺次竖着放)，即横竖摆放方案数相等

横向方案数：按列求，每列是否能摆只和上一列有关，将上一列列伸出小方格信息状压到32为(int)j中

定义：dp[i，j]为摆到第i列，上一列伸出小方格的行状态为j的方案数

j会用2进制数存i-1列伸出方格信息(如10010···101)

对于是否可转移：

• 条件1：(两列之间无冲突)： j(j前面列) & k(当前状态) == 0
• 条件2：列剩余格子应为偶数连续，用竖着方格填补空缺：j | k不存在连续奇数个0

状态转移方程：f[i，j] += f[i - 1，k]

将符合条件1，2的累加即可

对于条件2可以通过预处理完成(预处理合法摆放，而非真正去摆)
其中i < (1 << n)是预处理n = x的all状态

如n = 3，对应0 ～ 7(0～7的二进制对应(000)～(111))
枚举横向摆放：那么对于n行m列的盒子，枚举的其实是对于n行的情况(all行适用)

点击查看代码

while (cin >> n >> m, n || m)
{
    //预处理合法状态
    for (int i = 0; i < 1 << n; i ++ )//看的是0～2^n的数的二进制
    {
        int cnt = 0;
        st[i] = true;
        for (int j = 0; j < n; j ++ )
            if (i >> j & 1)//遇1则空白区间结束，进行判断
            {
                if (cnt & 1) st[i] = false;//奇数个
                cnt = 0;
            }
            else cnt ++ ;
        if (cnt & 1) st[i] = false;//不封口特判：j=(1000)不封口情况
    }

    memset(f, 0, sizeof f);
    f[0][0] = 1;//不摆放(第0列)为1种方案
    for (int i = 1; i <= m; i ++ )
        for (int j = 0; j < 1 << n; j ++ )//当前状态
            for (int k = 0; k < 1 << n; k ++ )//i - 1列的all状态
                if ((j & k) == 0 && st[j | k])
                    f[i][j] += f[i - 1][k];

    cout << f[m][0] << endl;//m-1列无任何伸出方格，此时0～m-1才为m列的合法方案
}

对于j=(1000)不封口，则cnt只会累加不会再进入判断是否为奇数，所以结尾要设置判断

最短Hamilton路径 P10447 最短 Hamilton 路径
Hamilton路径：经过all点且只经过一次

对于暴力：n! * n不可取，采用状压DP

对于1条通路路径，我之前的路径一定走了某一个点走到我，对all可能的点进行划分

定义：dp[i，j]为all从0走到j，走的路径方案为i(0/1当前点是否走过)

对于状态转移：假设上一步为点k，那么路径方案：0 ~ k路径长 +(k->j)边长(固定)，所以想让0～k路径最短 (每步最优 = 整体最优)

由于0～j路径为i，那么想要0～k路径即i - {j}(除去点j)的最小值：path(i - {j}) + a(k，j)边

点击查看代码

cin >> n;
for(int i = 0; i < n; ++ i)
    for(int j = 0; j < n; ++ j) cin >> w[i][j];
    
memset(f, 0x3f, sizeof f);
f[1][0] = 0;//0号点，只包含0这个点(二进制0为1)

for(int i = 0; i < 1 << n; ++ i)//i和j枚举all状态
    for(int j = 0; j < n; ++ j)
        if(i >> j & 1)//0走到j(一定包含j)
            for(int k = 0; k < n; ++ k)//从哪个点转移而来
                if(i - (1 << j) >> k & 1)//从k转移而来，去掉j后也要包含k这个点
                    f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][ n - 1] << endl;