字符串算法KMP&字典树

小技巧：字符数组伪string，下标从1开始

char q[N];
cin >> q + 1;

KMP求循环节：与处理每个长度的最大后缀 == 前缀
KMP

本质是与处理了模版串每个长度下的"最大后缀 = 前缀"
那么当第i位匹配失败后，直接移动到我长度的最大前缀(next[我])即可

例子:next[]数组预处理每个长度的前缀=后缀

当前不匹配时：
abcdcabcx
abcdcabcy

会退到next[我]
     abc···//接着往后看

kmp求循环节(字符串最小重复单元)
对于匹配：

• 匹配：往后看
• 不匹配：将模版串后移，直到和匹配串再次相等

再次相等时

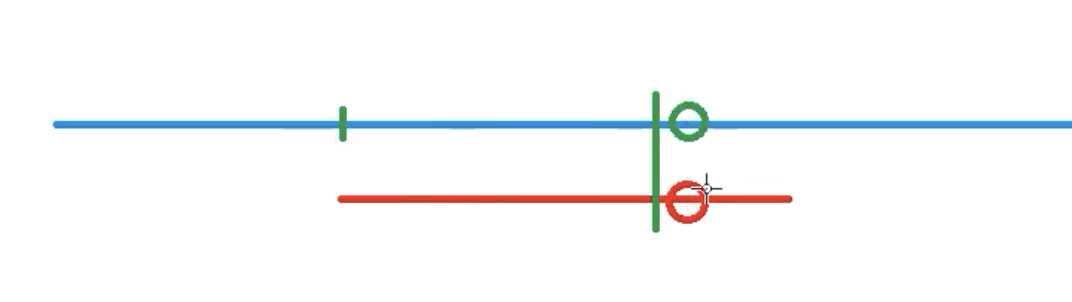
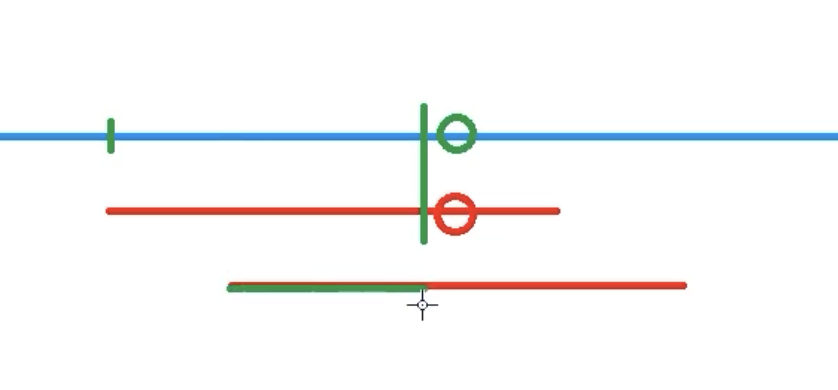
• [存在关系1]：蓝，红，绿三串相等

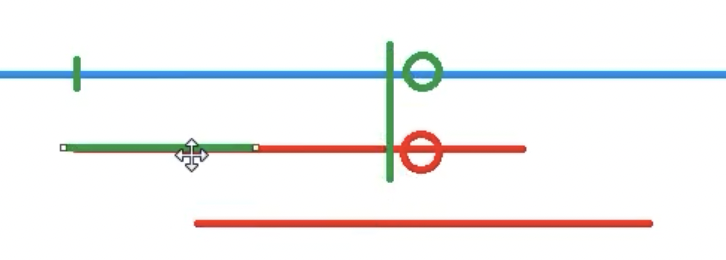
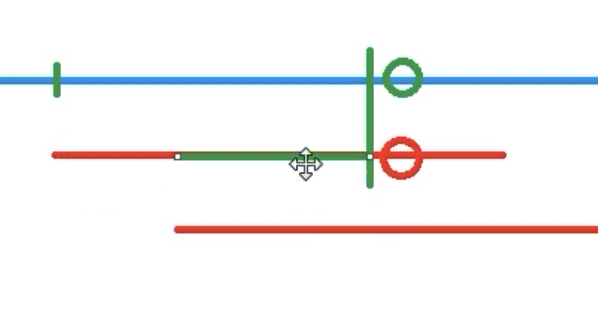
• [存在关系2]：平移得到的绿色段即是红色段前缀也是红色段后缀

结合关系1，2得出：发现有最多向后移动多少，只和模板串有关，即最大后缀 == 前缀

next[]数组： 模版串对每个点预处理出后缀：有前缀 = 后缀

有了next数组即可进行跨越操作(而不是遍历串)

通过j记录长度为i的子串中最大前缀=后缀(next[i] = j，j点为前缀下标)，且最小匹配长可以为0，所以我们定义看下一个点j + 1

每次让串更长：加入新字符与最大匹配点下一个进行匹配试图让最大前缀后缀更大

• 匹配：匹配点j后移，++ j，next[i] = j;
• (重点)不匹配：j = nextj

每次试图更进一步，不行则看我之前的最大匹配段(与我相同)是否和新加入相同，有则更进一步，无法匹配则看我之前的之前····直到会退到原点

for (int i = 1, j = 0; i < n; ++ i) {//自己！=自己，从1开始
    while (j > 0 && q[i] != q[j]) j = ne[j - 1];
    if (q[i] == q[j]) j ++;
    ne[i] = j;
}

匹配过程：不断尝试更大匹配的过程

for (int i = 0, j = 0; i < m; ++ i) {
    while (j > 0 && s[i] != q[j]) j = ne[j - 1];
    if (s[i] == q[j]) j ++;
    if (j == n) {
        cout << i - n + 2 << endl;//把下标变为从1开始
        j = ne[j - 1];//退回上一个最大匹配继续匹配
    }
}

Trie(字典树)： 字符树，通过标记记录是否存在

高效的存储和查找字符串集合，一般都为大小写字母，0/1

字符树，每个点存26条边(26字母)，依次存储字母，并在结尾处打上标记
通过idx给trie树分配唯一id
插入操作：

void insert(char str[])
{  
   int p = 0
   for(int i = 0; str[i]; i ++)
   {  
       int u = str[i] - 'a';
       if(!son[p][u]) son[p][u] = ++idx; 
       p = son[p][u];
   }
   cnt[p] ++;
}

查询操作：

int query(char str[])
{
   int p = 0;
   for(int i = 0; str[i]; i ++)
   {
       int u = str[i] - 'a';
       if(!son[p][u]) return 0;
       p = son[p][u];
   }
   return cnt[p];
}