最短路

最短路的all算法都可以在有向图中跑

前置知识：

• 稠密图： m ～ O(n^2)，邻接矩阵
• 稀疏图： m ~ O(n)，邻接表

dij大多数情况写堆优化，但当发现范围在1000且恰好边特别密，则可能只能写朴素算法

spfa很容卡，spfa可以处理负权边，也可以判断负权回路

当图有负权只能使用spfa，且spfa在图较随机，建图不好卡spfa的题中还是相对较好的，且spfa也是网络流中费用流的基础

Floyd
floyd的基础为DP，对权值正负没什么要求(所以对负权无所谓)

转移方程： d[i][j][k] = min(d[i][j][k - 1]，d[i][k][k - 1] + d[k][j][k - 1])

dijk有两种情况：

• 第一种ij之间最短路不走k：则只走一次1～k-1之间的边
• 第二种走k：即i～k之间的最短距离和从j～k的最短距离之和，两种情况取min

d[i][j][0]即不通中间节点，此情况下有边相连即边权值，没边相连即未连通

这里也解决问题：即为何floyd为什么要先枚举中间节点，也为floyd最容易犯的错误(写错枚举顺序)

floyd要先枚举中间节点，是根据其算法思想
然后进入上图算法流程即不会写错顺序

方便起见也可以不开ijk，用类似邻接矩阵开两维，在原地进行迭代

int d[MAXN][MAXN];

void floyd() {
    for (int k = 1; k <= n; k++) {//先枚举中间节点
        for (int i = 1; i <= n; i++) {//枚举i
            for (int j = 1; j <= n; j++) {//枚举j
                if (i != j && i != k && j != k)//三个点不同，则更新
                    d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

单源最短路
维护dis

松弛操作
如有一条u到v得边(u，v)，尝试用u的一条最短路径再走u到v这条边，看是否为v这条最短路径，若dis[v] > dis[u] +1(边长)，则将这条边更新

spfa

队列优化的bellman-ford

bellman-ford：对整张图进行n-1次松弛，每次以任意顺序枚举每条边···进行松弛

bm-fd正确性：
由于第一次松弛枚举了all的边，则与s相连的点一定是最新的，则第二次松弛时这些点也为最短(无论如何枚举)它们出边的点，保证长度为2的最短路也一定都是最新的，即每次松弛都会保证长度为i的最短路径枚举出

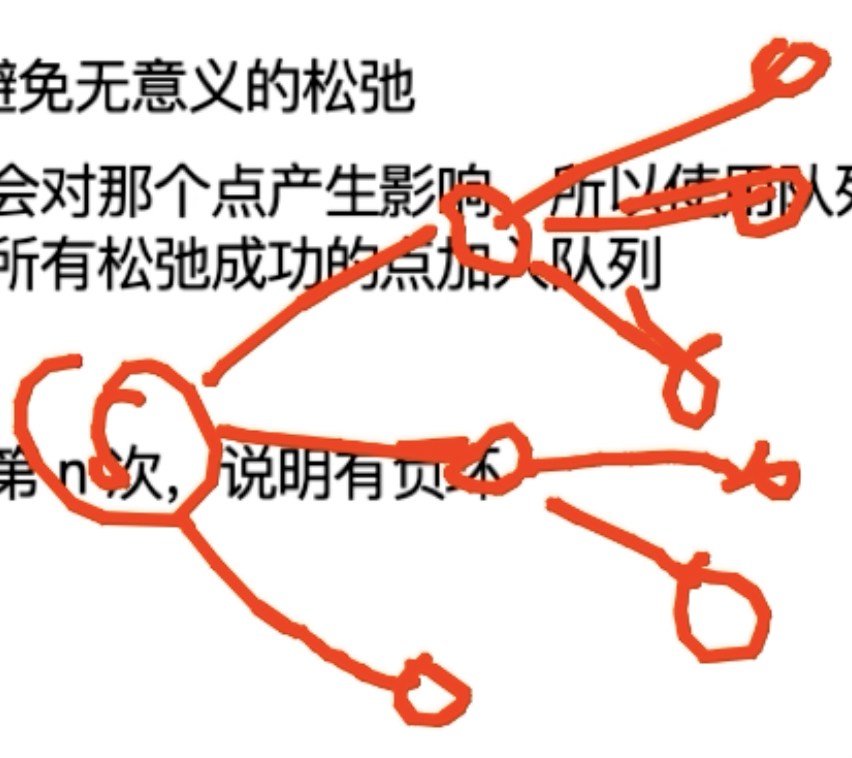
spfa避免了bm-fd无意义的松弛：
bm-fd松弛n次，每次对m条边全部松弛，但发现当松弛后：如松弛u到v(u，v)，只有u到v且u到v得值更新了，才会对v产生影响，才会对后续的点产生影响，用队列维护等待松弛的点，每次取一个点松弛时，将all松弛成功的点加入队列，即每次取u，对all松弛成功的点v，u到v有一条边(且u到v最短距离会通过走u到v边来走)，此时才加入队列(只有这样才需要对v点更新)

玄学优化，有各种卡方式

上述即spfa思想：
n-1次松弛后，all长度n-1的路径全都找出，此时一定能搜到最短路
但如果第n次还能继续松弛，则说明有一个长度为n的最短路(即存在环)：而存在环，但还未被去掉则说明环可以让最短路变小，则说明有一个负环

松弛同时维护all点次数，松弛n次：说明有负环

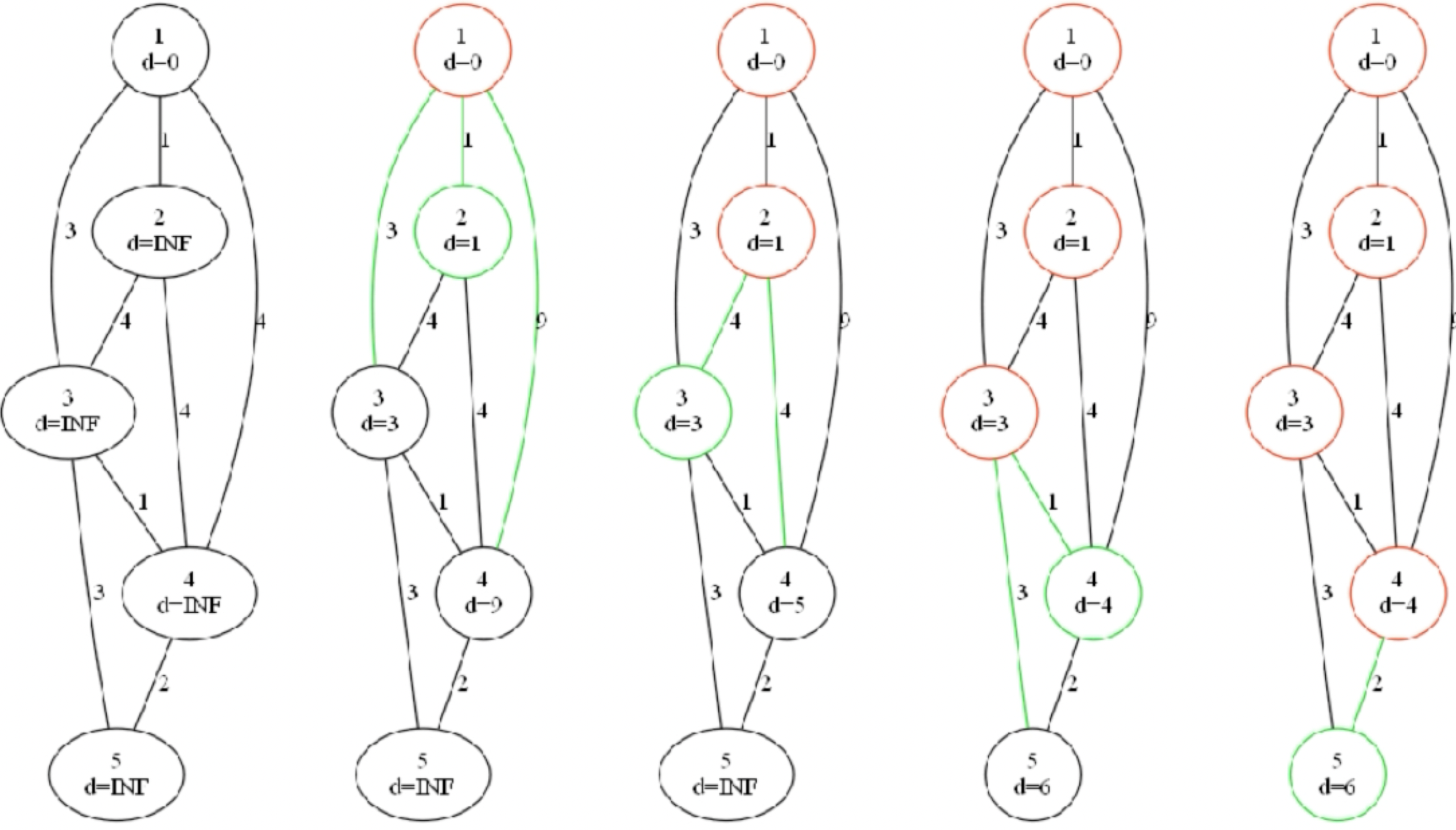
流程图：(红色正在处理，绿色指入队)

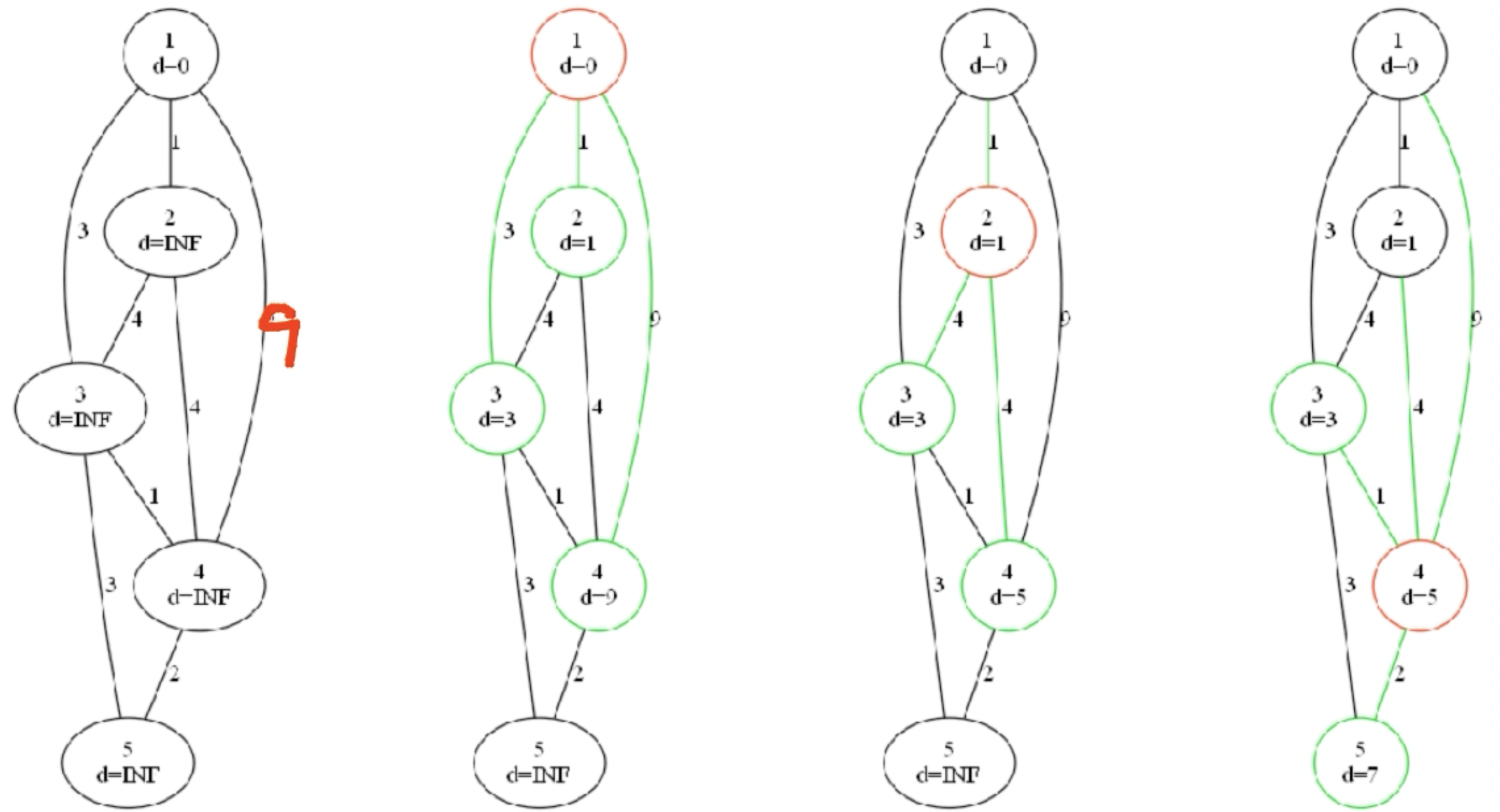
以1号点为起点，d=0，其余all点距离为INF，最开始将点1入队，更新点1相连的all的边，通过1，3，9这三条边成功将点2，3，4距离更新，然后以任意顺序访问这三个点，如枚举点2，依次枚举点2all边(往回走的1不能走，算出2；往3走算出长度5，大于3不更新；往4走长度5，更新，点4从9变为5)，将点4加入队列(但已经在队列中)

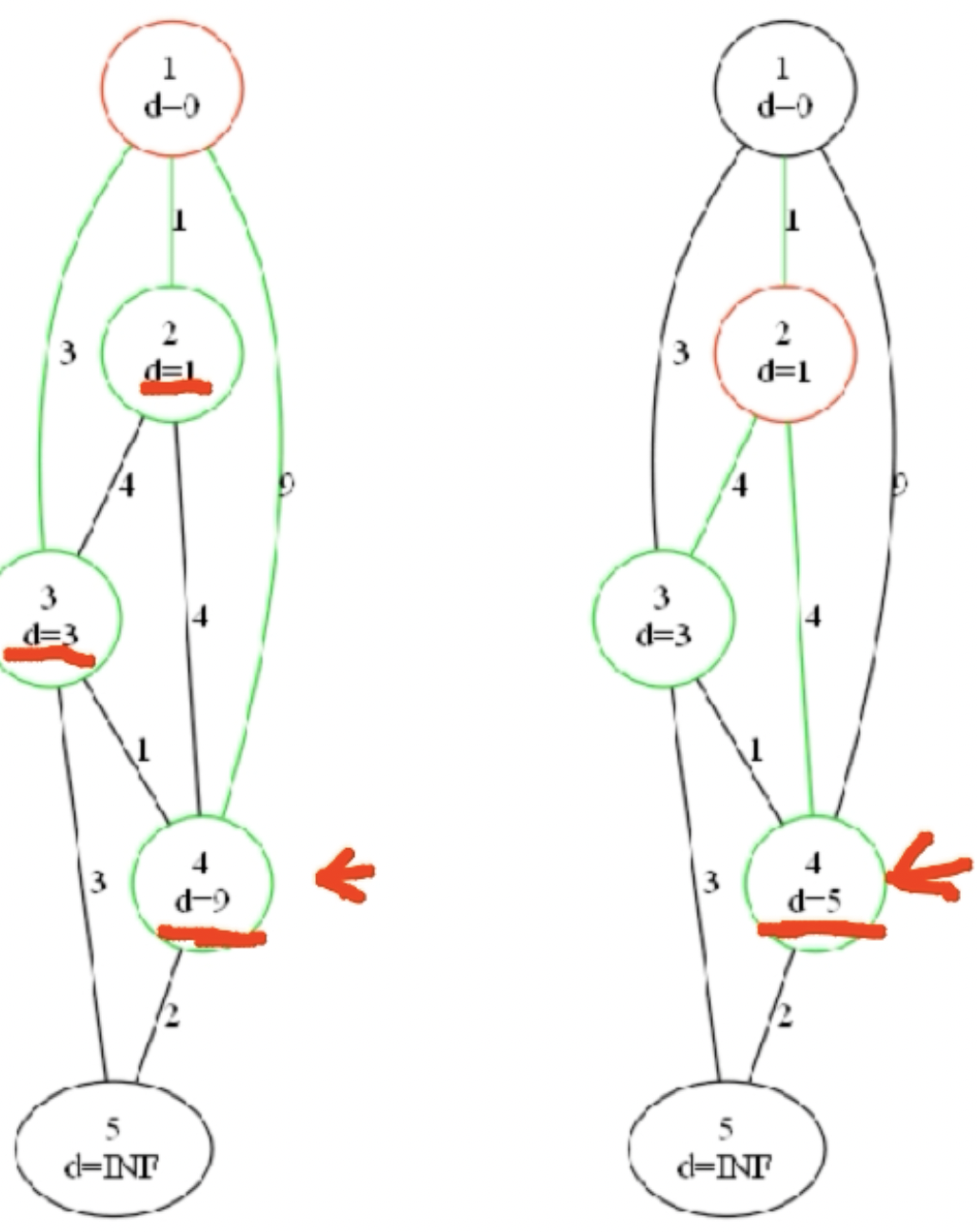
(要注意)spfa中：当一个点已经在队列中，不能重复入队

继续随机访问3，4号点，如访问4号点距离5，顺着点往回更新，发现可以更新到终点距离7，然后将终点加入队列，此时队列有3，5号点，先访问点3，距离为3，无法往上更新，但往下可以将点4更新(虽然点4被更新入队，但又一次被更新又要入队(也仍然更新其他点信息))，也将点5更新为6···最后结束

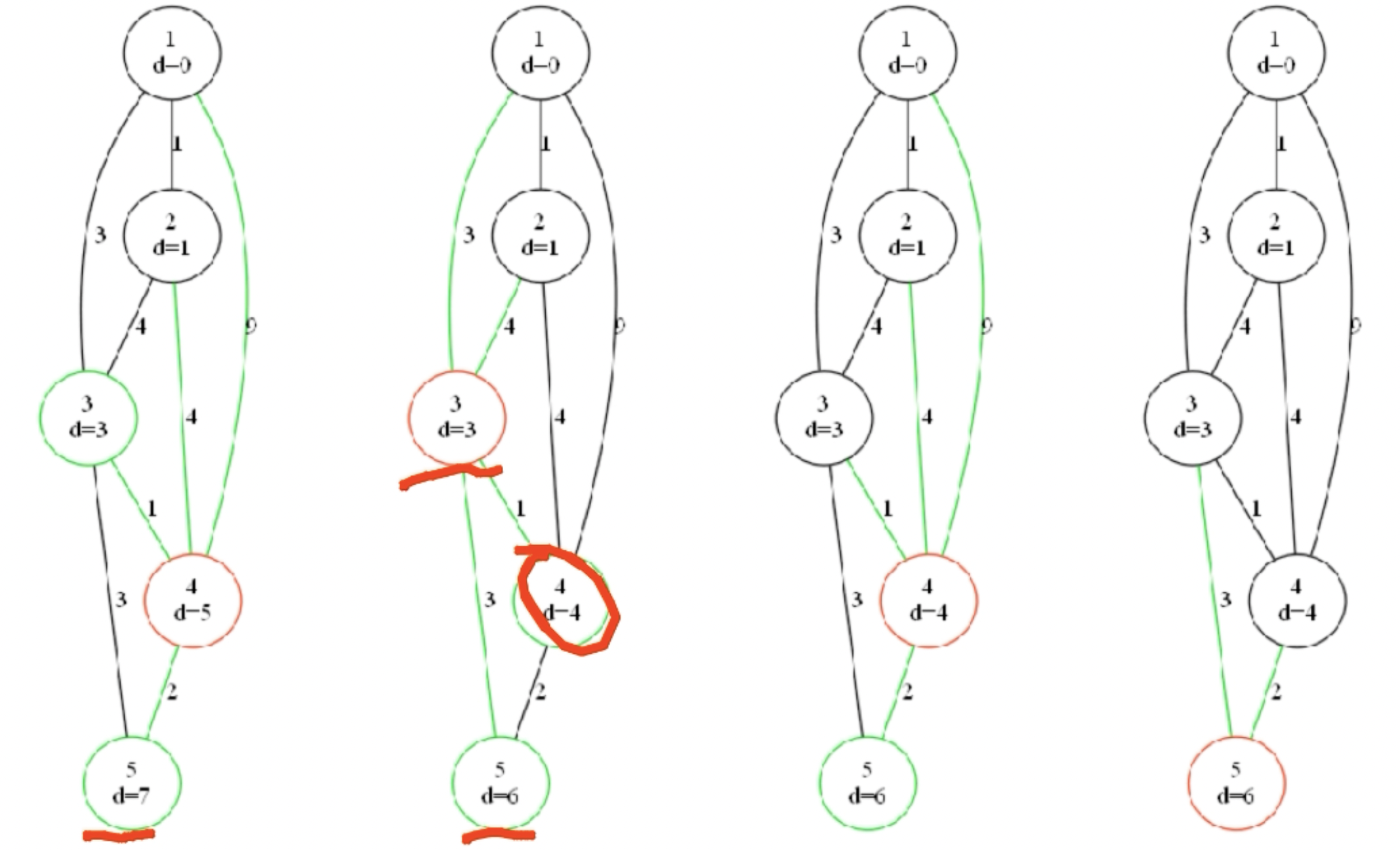
这个过程中，每个点将多次入队

spfa类似多次bfs的一个东西

点击查看代码

bool inq[MAXN];//维护某点是否在队列中：入队标记，出队删除
//若没删访问标记会有错误答案，若未访问标记会死循环，若未判访问标记会特别慢/死循环
queue<int> q;
//存图方式：使用链式前向星
inline int spfa(int s, int t) {
    q.push(s);//这里直接用STLqueue，是因为一个点可多次入队
    //之前，手写队列因为知道队列长度：不光队列长度n，至多进队的元素次数也是n
    //这次虽然队列长度至多n，但一个点可能多次入队，最终走的次数可能非常多
    //若手写队列则要写个循环队列，不值得
    inq[s] = true;
    memset(d, 0x3f, sizeof(d));
    d[s] = 0;
    while (!q.empty()) {
        int now = q.front(); q.pop();
        inq[now] = false;
        for (int i = he[now]; i; i = ne[i]) {//枚举每条出边
            Edge &e = ed[i];
            if (d[now] + e.dist < d[e.to]) {//取一点now，枚举其all出边
                                            //若这个点到那个点两个点走的
                                            //路径可以更新最短路长度，执行松弛操作
                d[e.to] = d[now] + e.dist;
                if (!inq[e.to]) {//若不在队列(成功执行松弛操作：点应在队列中)，加入队列
                    q.push(e.to);
                    inq[e.to] = true;
                }
            }
        }
    }
    return d[t] == INF ? -1 : d[t];
}

SPFA若干玄学优化

在于它的加入队列这步

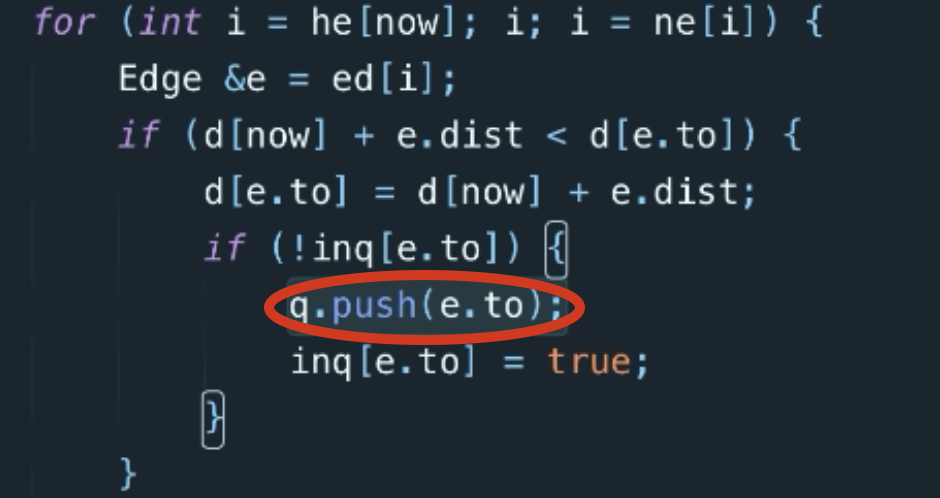
一般情况直接spfa队列扔到尾部算了，但因为spfa是一个队列(其实访问队列中任何一个元素都是可以的)

启发说，能否用奇技淫巧将队列中的顺序不是每次都往后仍，能不能防一些卡(防止出题人的卡)呢？
于是就有了若干优化：
如小的比前面小的就放前面，如果它大放后面···的两种SLF和LLL优化

但其实打了这两种优化也会被特殊情况卡掉，不如dijkstra
无负环果断dijkstra

Dijkstra
将起点作为已访问集合第一个点，更新相连的点(松弛)···，找到离起点最近的点，标记已访问，更新相邻点

根据"找到未被访问的dis最小的点"分为两种：

• 直接枚举每个点，看哪个点dis值最小
• 当某个点距离更新时，将这个值(dis[u]，u)插到小根堆中，从小根堆中取的点即dis最小的点(但要注意dis最小的点必须为未访问的点)

即可能前面已访问：如先插入5，3进去，又有一个更短路径插了(3，3)进去，这个点先出队，

(3，3)更短，并且使得这个点变为已访问信息处理完成，再遇到(5，3)时即跳过

过段时间则枚举到(5，3)，这个点信息其实已经处理完只是未被删掉，直接不处理它即可(并不好在堆中删元素)

流程图：

首先1号点，枚举出边更新(松弛)，不同的是发现2号点其他点中最近的点，加入队列处理，点2有将点3更新为3，将点3处理标记访问(3更新4，5号点)，有4号再次被更新，···然后4，5号点

点击查看代码

int d[MAXN];//距离
bool vis[MAXN];//是否访问
//队列，定义小根堆(考场没那么多时间手写堆，斐波那契堆)
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
int dijkstra(int s, int t){
    memset(d, 0x3f, sizeof(d));
    d[s] = 0;
    q.push(make_pair(0, s));
    while(!q.empty()){
        int now = q.top().second;
        q.pop();
        if(!vis[now]){//若被访问过，就说明它是这个点的
                      //次大或第三大之类的，说明不是最小dis值
                      //说明这个点被处理过了
            vis[now] = true;
            for(int i = he[now]; i; i = ne[i]){//枚举出边
                Edge& e = ed[i];
                if(d[e.to] > d[now] + e.dist){//松弛
                    d[e.to] = d[now] + e.dist;
                    q.push(make_pair(d[e.to], e.to));//将点信息插入堆中方便下次枚举
                                                     //这里pair两个参数，第一个参数点的距离，第二个点的编号
                }
            }
        }
    }
    return d[t] == INF ? -1 : d[t];
}

点击查看代码

//思想：1.最短路问题中如果all边为正,自环显然不会出现在最短路
//      2.重边,则两点之间只保留一条长度最短的边即可
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
int g[N][N];
int dist[N];//Dijkstra中从1号点走到每个点的距离是多少(当前最短距离)
bool st[N];//每个点最短路是否确定
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//所有边初始化为正无穷
    dist[1] = 0;//1号点距离为0
    for(int i = 0; i < n; i ++)//迭代n次
    {//每次找到最小值(找到当前没有确定最短路长度点当中距离最小的点)
        int t = -1;//未赋值
        for(int j = 1; j <= n; j ++)
        if(!st[j] && (t == -1 || dist[t] > dist[j]))//t=-1，若不存在候选点则默认j为候选点
        t = j;
        if(t == n) break;
        st[t] = true;//t加入集合
        for(int j = 1; j <= n; j ++)//拿t更新其他点的距离
        dist[j] = min(dist[j], dist[t] + g[t][j]);//用1到t距离+t到j这条边，来更新1到j路径长度
    }
    if(dist[n] == 0x3f3f3f3f) return -1;//不连通
    return dist[n];//最短路径
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(g,0x3f,sizeof g);
    while(m --)
    {
        int a,b,c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);//a和b之间可能有多条边，只保留长度最短的那条边
    }
    int t = dijkstra();
    printf("%d\n",t);
    return 0;
}

dj正确性证明中用到了边dist的单调性(按这个顺序访问dist不会再往下走)

但这个在负权显然不成立

e.g.

已开始更新为1，后续通过2又被更新-6(虽然被更新过，但由于负权边导致再次被更新)，所以这也是为什么dj无法处理负权边(dj每个点只会更新一遍)

其中对于dijk为稀疏图情况，两重循环\(10^10\)即会爆空间，即引出堆优化版dijk

(堆优化)dijkstra