栈&队列

单调栈：维护单调性，保证单调性维护最小/大弹出

• 主要是压栈和弹出的顺序性
  

模版题P5788 ：

点击查看代码

for(int i = n; i >= 1; -- i) {    
        while(!s.empty() && a[i] >= a[s.top()]) {//栈顶与当前比较，维护单调
            s.pop(); 
        }
        b[i] = s.empty() ? 0 : s.top();//某些题可开记录数组
        s.push(i);
    }

栈中存下标维护了位置信息，通过a[s.top()]取值，题目要求输出下标

P2866
思路：同理P5788，维护将序，输入>栈顶(弹出)，b[i] = i - 1 - s.top()(看到的最大距离 = 比我高元素的前一个元素即i-1 - 我的位置)

中缀表达式用栈转后缀表达式，后缀表达式用栈转表达式树
表达式树
如：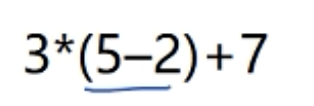
画一个加号，然后其右边连接7，它的左边连接3*(5-2)这一坨东西(先画一个乘号，连接执行它的元素，左边连3，右边连5-2(先写减号，然后连接其两个元素 ))

表达式树即由底向上算值

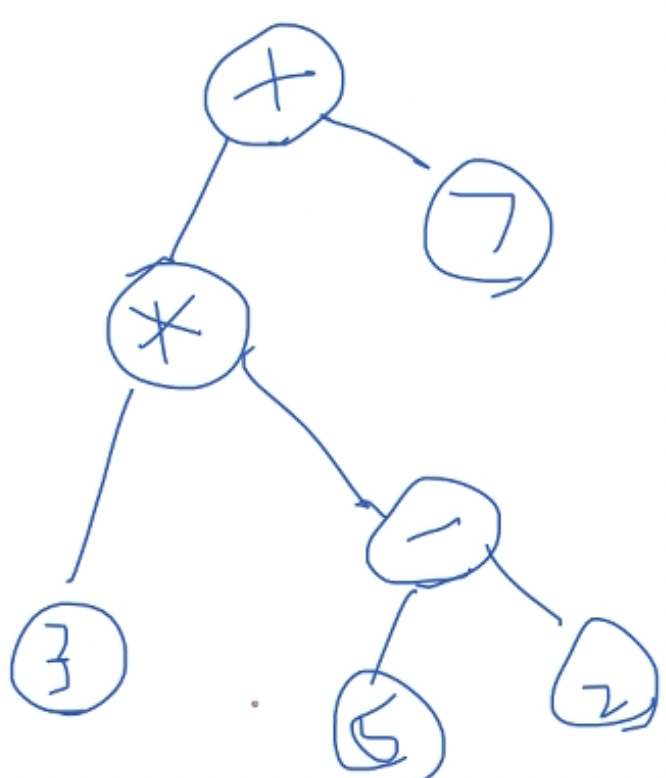
这坨东西即左边这坨+7，左边这坨即3乘上右边这坨(5 -2)

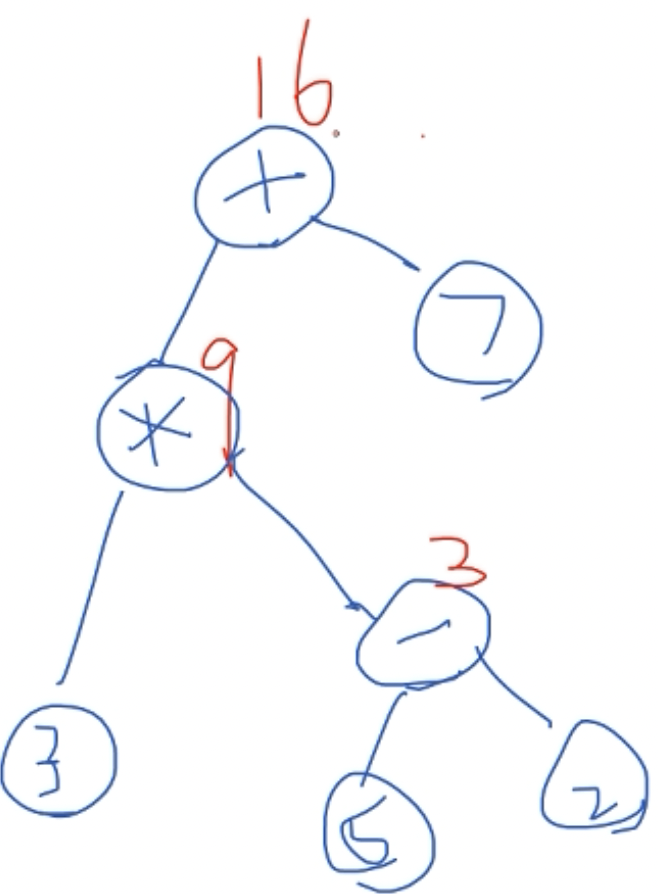
即只有叶节点为数，其他都为符号

表达式树对比栈求值好处：表达式可支持未知数
假设3*(5-x)+7，算出表达式值：
即不知道x多少，也要将x分析，则可用过表达式树(x为叶子节点)，当值知道后代入即可

中缀转后缀： 维护运算符栈，有数直接输出，将预算符存到栈中维护
后缀表达式求值： 维护数栈，遇到运算符进行弹出运算再插入的过程

循环队列： 采用[下标%n]方法，将队列空间限制在一个区域内，解决空间被浪费的问题
这里采用&上什么东西-1(卡常写法)，且要求MAXN一定是2的某次幂

const int MAXN = 1 << 20;//一定为2的某次幂
struct Queue {
    int l, r, q[MAXN];
    Queue(): l(1), r(0) {}
    inline void push(int x) {
        q[++ r & MAXN - 1] = x;//MAXN-1使得为011····111
    }
    inline void pop() {
        ++ l;
    }
    inline int front() {
        return q[l & MAXN - 1];
    }
    inline bool size() {
        return l <= r;
    }
};
Queue Q;
int main() {
    Q.push();//.pop()/.front()/.size()
    return 0;
}

单调队列：滑动窗口：发现对于动态区间问题，某些元素一定不是解，则通过双端队列通过插入弹出维护单调性

//维护单调
if(!Q.empty() && i - k + 1 > Q.front())//已经脱离窗口，弹出 
    Q.pop_front();
while(!Q.empty() && a[Q.back()] >= a[i])//新插入<队尾，维护单调弹出
    Q.pop_back();

通过比较新元素和back元素来维护单调性，从而优化题目

模拟版：

hh = 1, tt = 0;
for(int i = 1; i <= n; ++ i) {
    if(hh <= tt && i - k + 1 > q[hh]) ++ hh;
    while(hh <= tt && a[q[tt]] >= a[i]) -- tt;
    q[++ tt] = i;
    if(i >= k) cout << a[q[hh]] << ' ';
}