基础思想&搜索枚举:无后效性:这个点的结果是固定的
快读defiine大法:
#define read(a) {char c;while((c=getchar())>47) a=a*10+(c^48);}
位运算:两操作类型按位
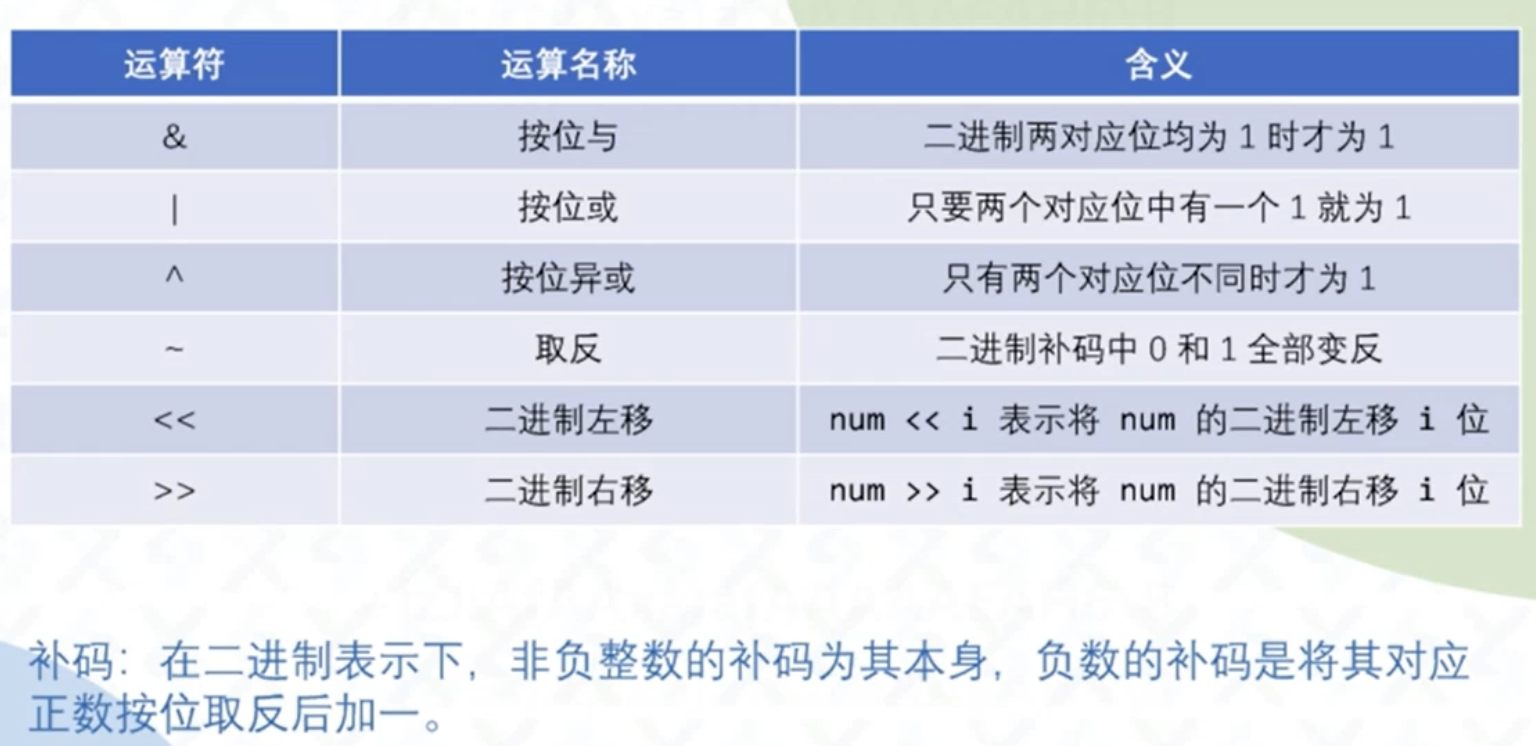
位运算应用:
- 状态压缩(小范围数压缩到int空间等)
- 取二进制数某一位:将其右移到最右边那一位&1
- 将二进制数设为0/1,取反

unsetBit:把目标位设置为0,其余都为1,然后进行&操作,则目标位 = 0
setBit:任意|1 = 1
flagBit:翻转,取0/1进行^(异或)即可
bitset:

频繁对0/1操作 => 考虑bitset,bitset本质上类似unsigned long long,封装在一个易于使用的集合
bitset<>:<>中非类型,而是大小
bitset:将集合,位运算集成在了一起
对于每次操作n,可以弱化操作n/64,一次操作可以动64位
对于n^3算法 => 变为 n^3 / 64 = 1.···* 1e7
P1100:
unsigned int不用担心正变负,可以将乘不下位直接抹掉
此时(x << 16) + (x >> 16) = 16低位16个0 + 16个016个高位 = 高地位交换16位
对于C++很多情况,<<左移都为逻辑左移(不考虑符号位),将1移动到符号位则会变为负数(会移掉负号,移出负号)
右移:正数是逻辑移位往前补0,负数是算数移位往前补1
B3632:

点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, x;
bitset<64> a, b;
int main() {
cin >> n;
for(int i = 1; i <= n; ++ i) {
cin >> x, a.set(x, 1);
}
cout << a.count() << endl;
cin >> m;
for(int i = 1; i <= m; ++ i) {
cin >> x, b.set(x, 1);
}
bitset<64> c = a & b;
for(int i = 0; i <= 63; ++ i) {
if(c[i]) {
cout << i << ' ';
}
}
cout << endl;
c = a | b;
for(int i = 0; i <= 63; ++ i) {
if(c[i]) {
cout << i << ' ';
}
}
return 0;
}
搜索
暴搜:也可以处理调整顺序问题,P1088(字典序排列方案)
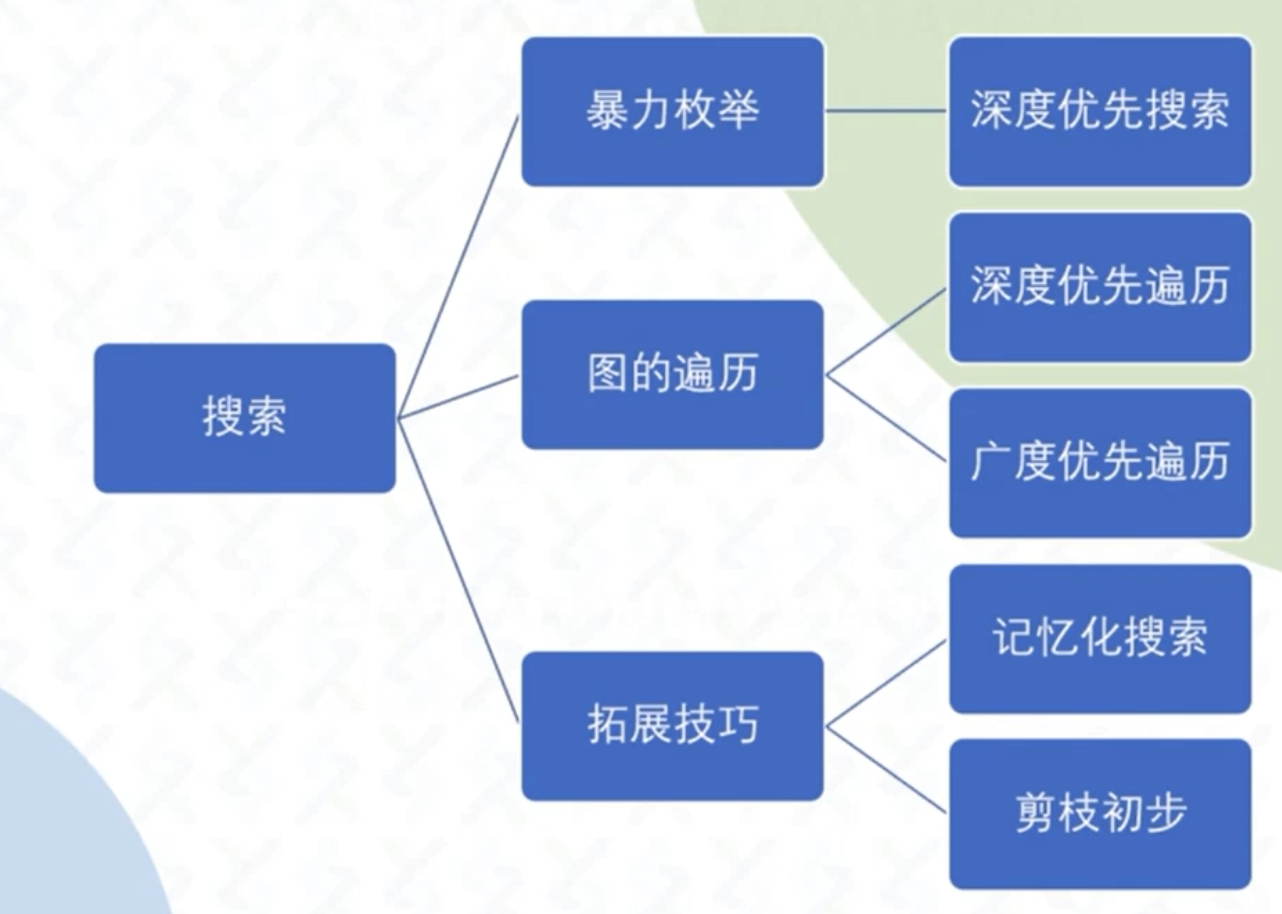
暴力枚举:

框架:例子是p1157

点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n, r;
int a[25];
void dfs(int u, int k) {
if(u > r) {
for(int i = 1; i <= r; ++ i) {
cout << setw(3) << a[i];
}
cout << endl;
return ;
}
for(int i = k + 1; i <= n; ++ i) {//当前数从k开始,使得方案递增
a[u] = i;//方案数组存方案每一位
dfs(u + 1, i);
}
return ;
}
int main() {
cin >> n >> r;
dfs(1, 0);
return 0;
}
图的遍历:DFS/BFS:例题是P5318
图的DFS:即存图,然后走友邻

图的BFS:将访问点加入队列,然后处理队列即可


记忆化搜索:记录走过点的信息
无后效性:确定性,不因其他原因影响的这么一个状态
有后效性:即会根据某些因素导致最终状态不同
也因为无后效性,从而记录值才是有意义的(固值),有后效性则可能会出现多个不同的值

例题:P1434滑雪
滑雪即符合无后效性:对于某些结点,呈现出能滑行的路径 (固定的:即无论从哪个点到这个点,这个点往下滑的最长路径不变)
第一种
if(dp[x][y] != -1) return dp[x][y];
f[x][y] = ans;
return ans;
第二种
dp[a][b] = max(dp[a][b], dp[x][y] + 1);
return dp[a][b];
第三种
return dp[a][b] = ans;
剪枝初步:分为可行性剪枝和最优性剪枝
可行性剪枝:若当前状态已经不可用,直接返回
最优性剪枝:若当前状态已经比ans更差,直接返回

例题:B3624
对于当前选的食物+没选的食物总和 < L(到不了L),那么直接返回即可
贪心:贪心要证明!
也符合无后效性,大问题转化为小问题,再由小问题求解大问题

反证法:考虑偏序
反证法是现有方法按照xxx规则去做判断
即假设当前方法是错误的(可能替换,交换,顺序等),变化后是正确的,此时只需证明无论如何改变,得到的结果都不会比目前方法更优,那么就没法证明变化后是正确的,则当前方法正确
归纳法(数学归纳法 => 数学公式):
- 证明:在起点是对的
- 在某个点是对的 => 到更大/更远的点也是对的
或者对于Fn都可以由fn-1构造出也可
具体即当n=1成立,n=x-1成立可推n=x成立,则有n=1=>n=2=>··,则成立
(hack)构造反例:试着让程序错误

例题:p1208
反证法例子:对于n个任务,每个任务需ai时间任务(每项任务有截止时间di),做all任务最小时间:
即按照截止时间di小到大去做
反证法:任意更换两项,一定有截止时间长的被移动到了前面(d2,d3交换),又因为按顺序去做,那么一定要使得原本all < d3变为all < d2,那么得到最小工作量 = (all / d2 > all / d3)

二分:二分查找和二分答案
二分查找:
- 基于序列有序(单调)
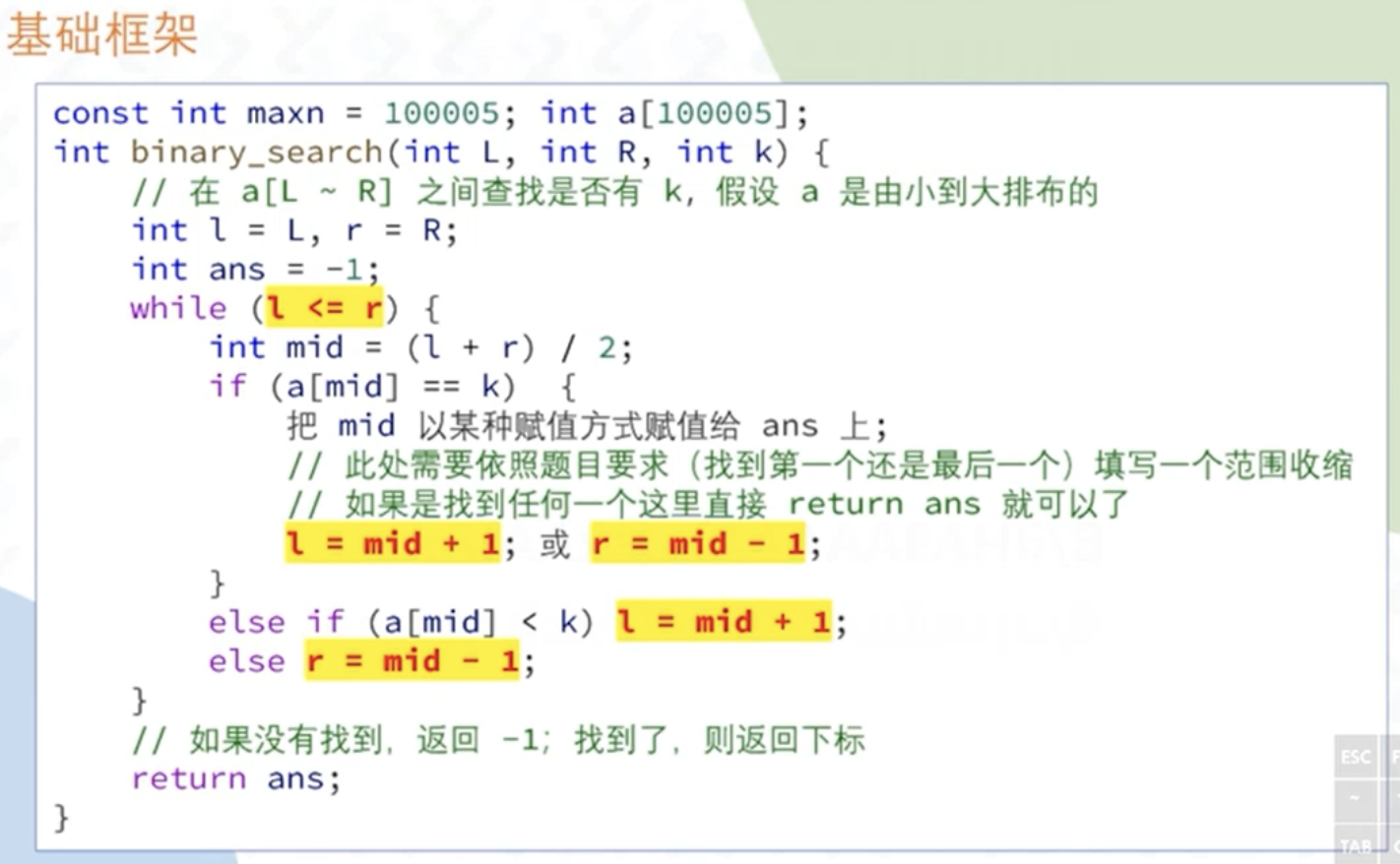
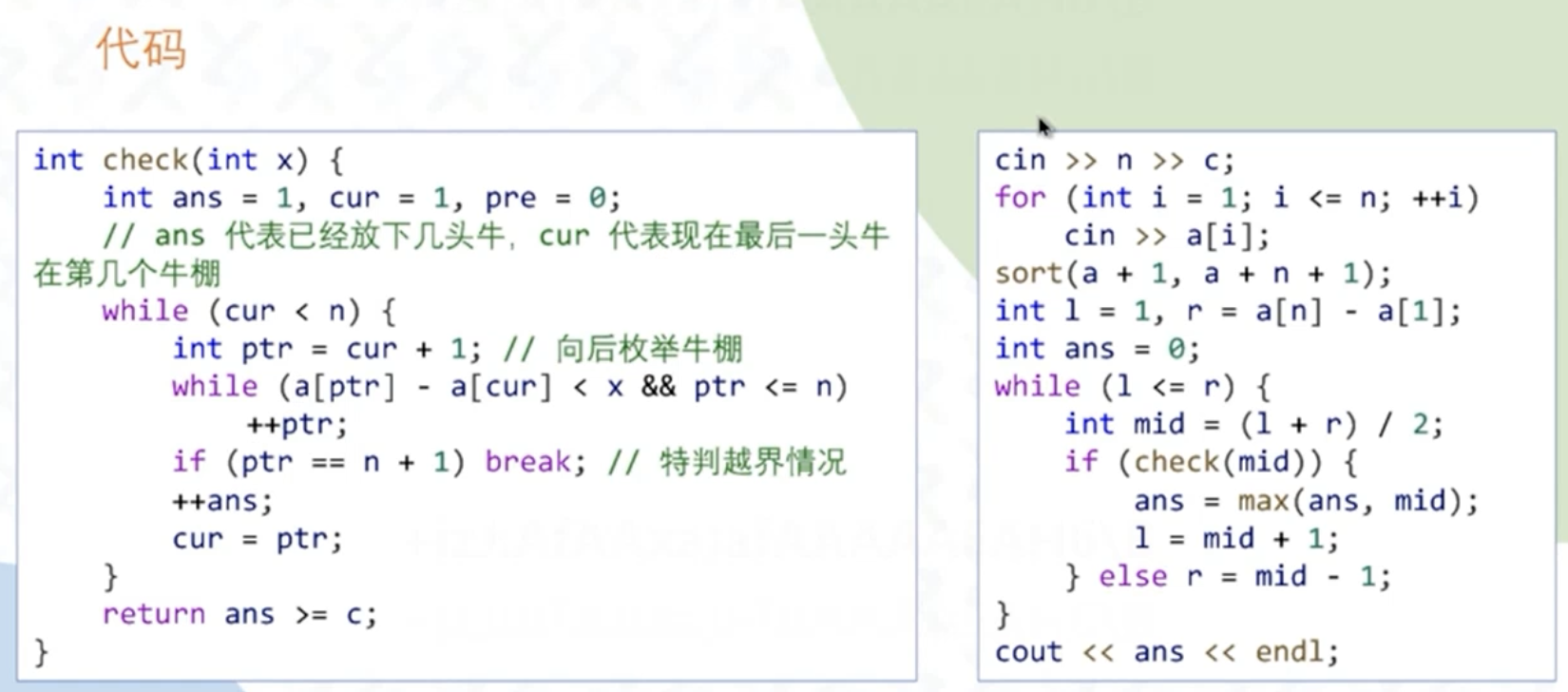
二分答案:

二分答案常见问题:

框架:

例题:p1824
前缀和与差分
前缀和:前n项和
大幅度降低查询区间值的时复
预处理前缀和数组:存起始到我的总和

前缀和数组
定义:

如二维数组即范围值,多维类推
实现方式:

一维:f[n] = f[n - 1] + a[n];
那么对于求区间和[i, j],只需要用f[j] - f[i - 1]即可
二维:
构造二维
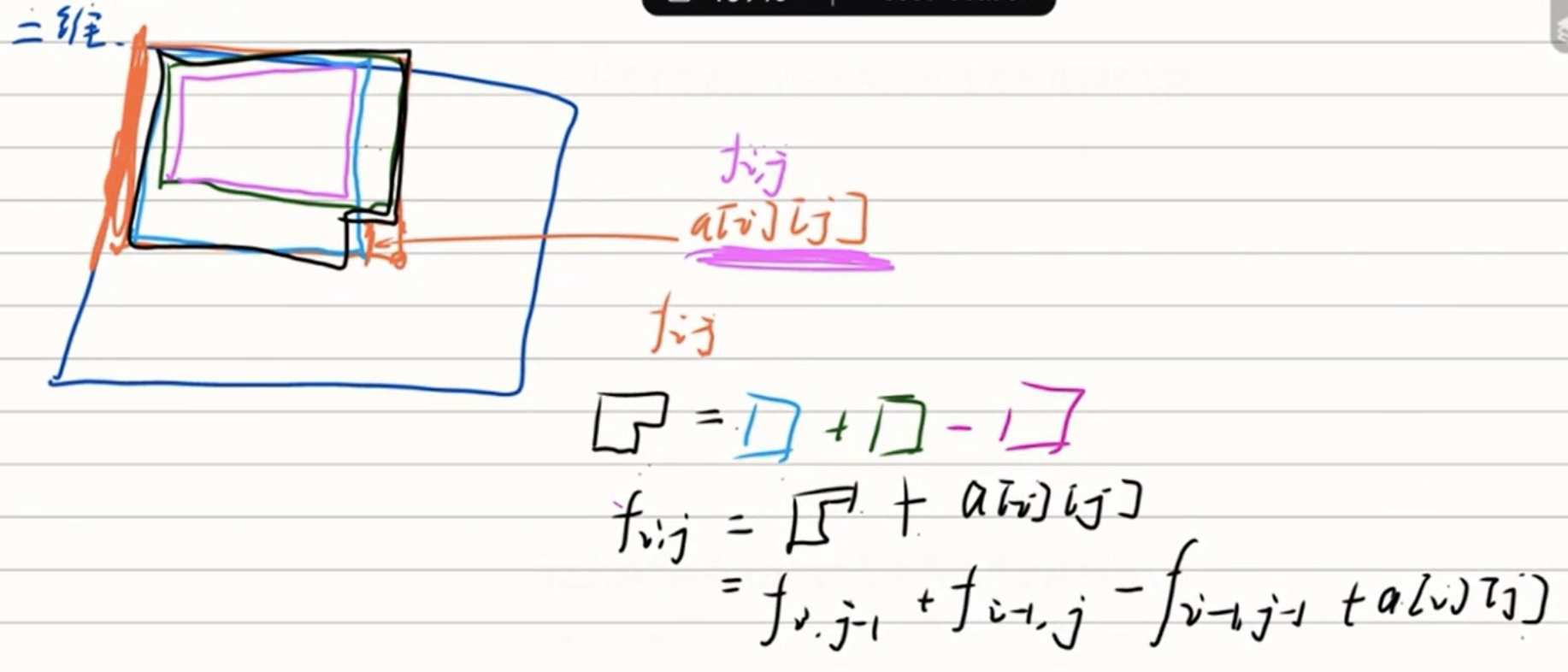
查询二维:理清逻辑即可
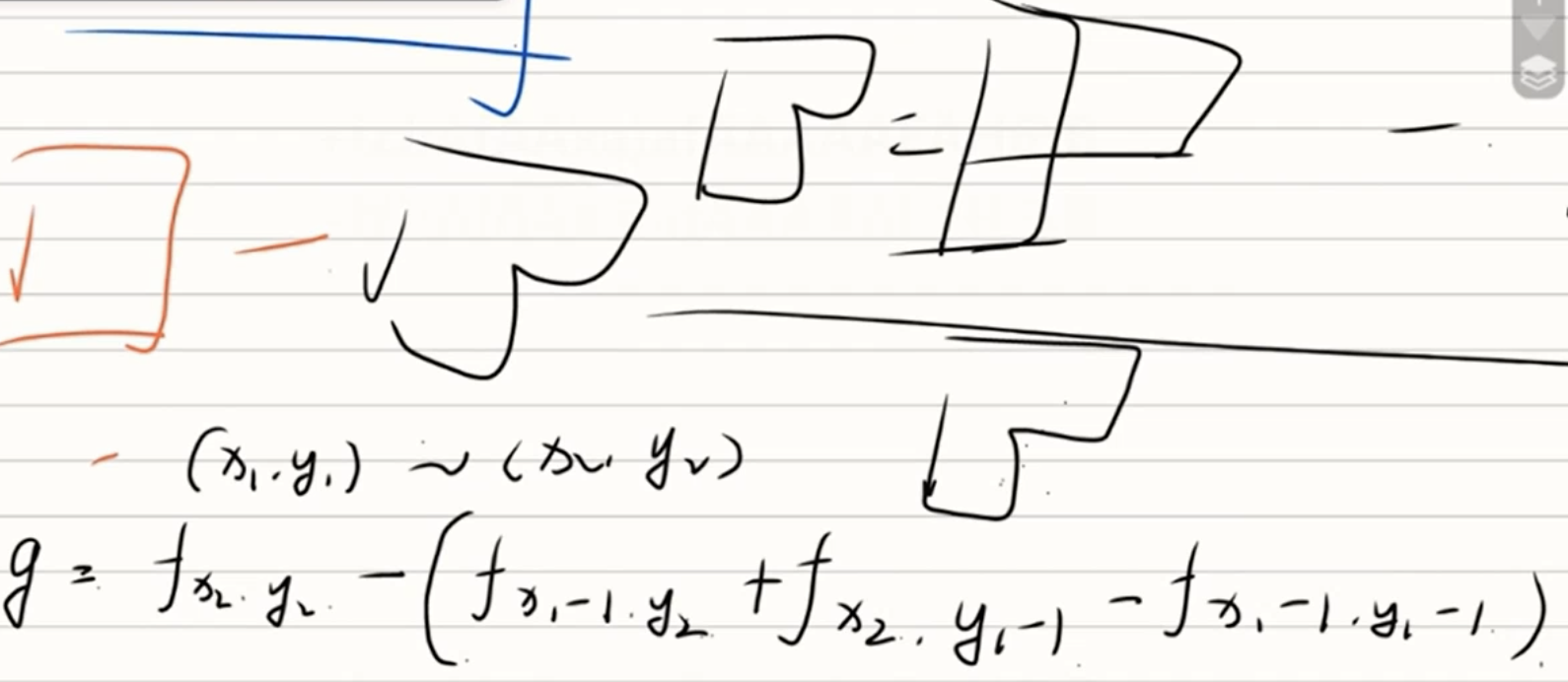
多维前缀和:容斥原理
差分:多次修改但最终只有一次查询的复杂度
差分数组的应用:
- 求改动后区间大小
- 单独使用也可以维护区间是否存在(是否有值)
当不断累积即(!=0时)那么一段区间是存在值的
前缀和的逆运算
常应用于多次修改,统一查询的题
维护差分数组:记录该元素与其前一个元素的差值
概念:

作用:
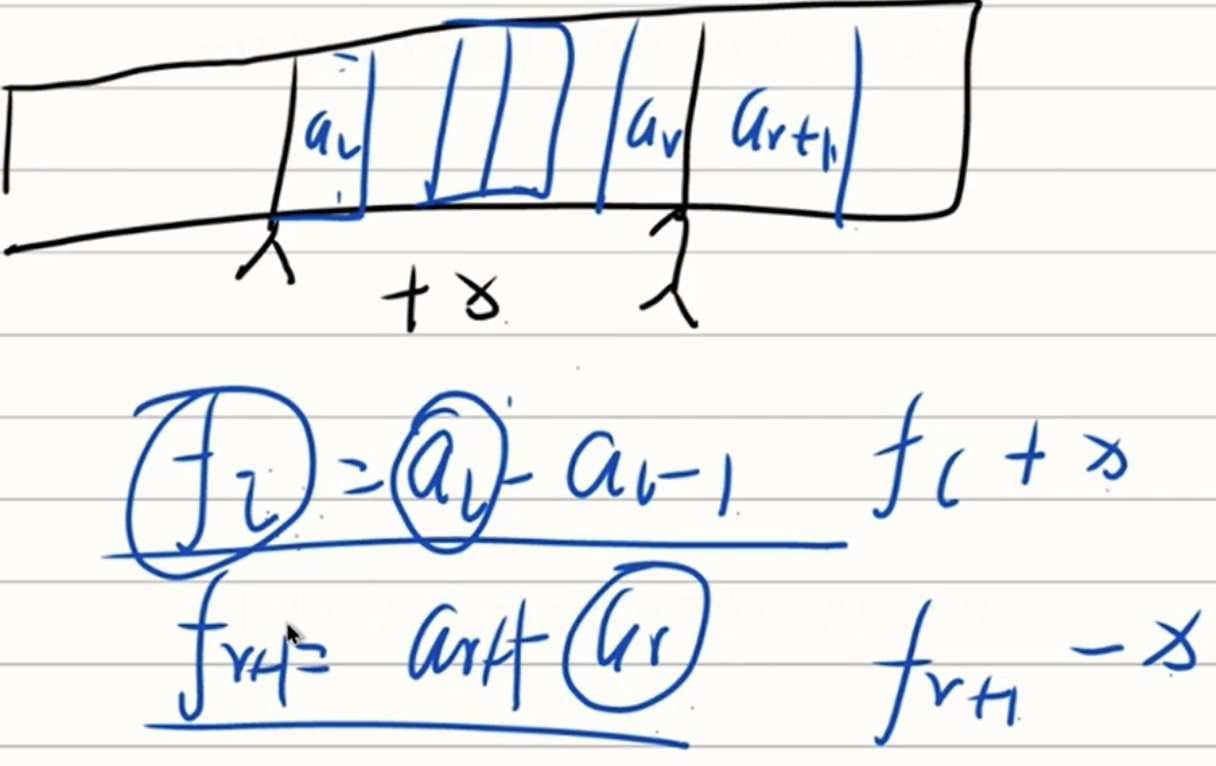
对于(l,r)区间上,在al一个点上+x,那么对应fi也就+x,此时对ar+1 - x,再对区间求前缀和即构造出(l,r)区间整体+x的操作
因为差分数组本质:ai - ai-1
所以前缀和即:a1 + a2 - a1 + a3 - a2···· = an,那么an即答案

代码:
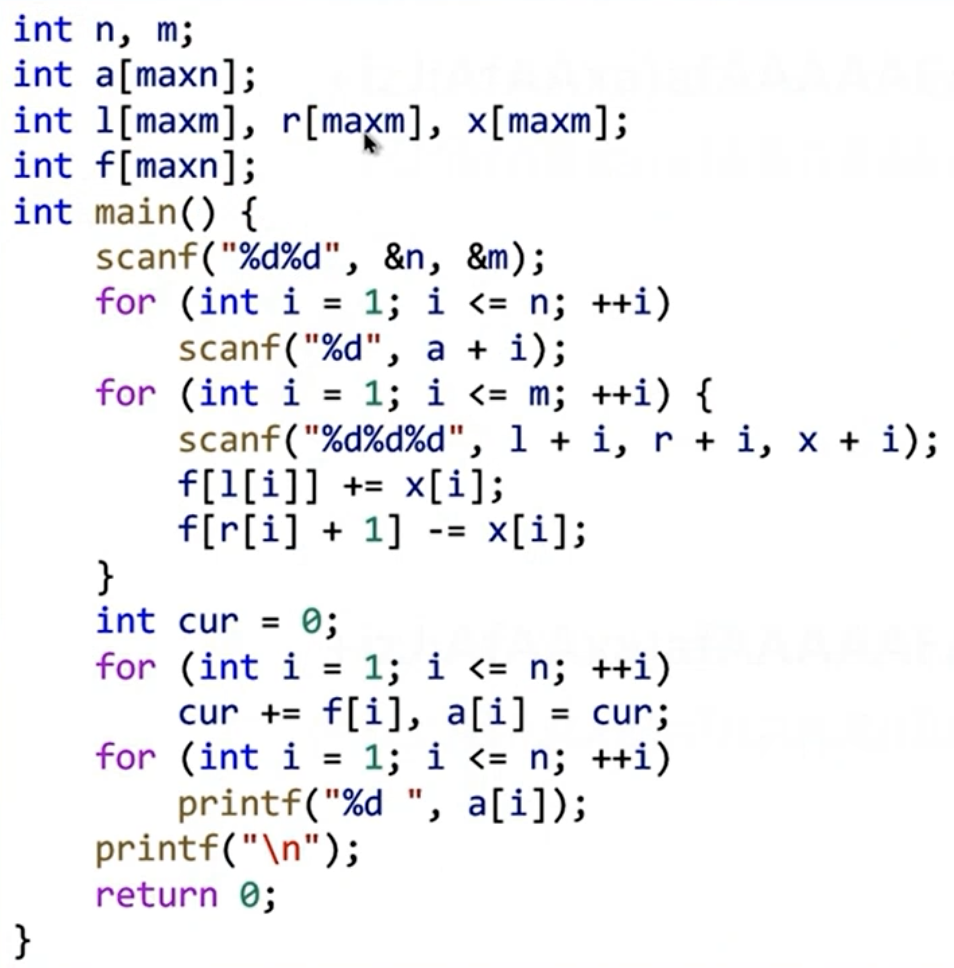
二维差分: 即当(x,y)点加上一个数,想清楚影响的区域(对多减少补即可)
差分数组表示"在全零矩阵上做的增量"
直接读入 a[i][j] 到 b,就打乱了差分结构,差分数组不是原数组,它只存储“变化的起点/终点标记”:
对于读入:使用
ins();//插入
区间修改:
如:在(x1, y1)到(x2, y2)区间增加k
a[x1][y1] += c;
a[x2+1][y1] -= c;
a[x1][y2+1] -= c;
a[x2+1][y2+1] += c;
对于查询:对增量求前缀和
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];//拼凑然后减去二次减的地方
双指针:维护区间
双指针:双指针(尺取)
找东西,维护区间和,快慢指针找环

查询目标值,例题:P1102
维护A-B=C
- 若A - B > C:让B前进,使得结果C变小
- 若A - B < C:让A前进,使得结果C变大
有一直把双指针维持在一个范围内,B指针跟着A指针动(因为A-B)
维护区间和,例题:p1147
也同为同向指针,维护区间和

快慢指针找环






 浙公网安备 33010602011771号
浙公网安备 33010602011771号