DP衔接(拼串:进行长度构造)

状态之间视为点，状态的转移为点之间的有向边，则会构建一张DAG

无环：不会确定后面的值之后再去更新前面的值

根据上面思路：
无后效性： 当一个状态确定，则不会被后面的状态所影响

即算f[5]时，与f[5]前面的f[2],f[3]无关···即不关心前面(即使有多种算法)如何算出，只保证f[i]为最优

最优子结构： 子问题的最优解可以推导出整个问题的最优解

DP三要素：

• 状态：描绘局面
• 转移：状态间计算关系
• 阶段：计算状态的顺序

对于DP思考路径，往往考虑状态的由来和状态的去处

一维线性DP：状态定于与题设为线性相关DP

LIS为一条线，为一维线性DP，而如棋盘问题，为棋盘二维，为二维线性DP

再看LIS(n^2 => nlogn做法)：维护LIS每个长度下最小结尾(单调) + 二分

对于朴素的LIS，会对其前面all元素都进行一次比较尝试更新，但其实对于长度为x + 1的值来说真正有用的只有前面长度为x的那几个值，发现对于相同长度的LIS，显然结尾的数越小越好(后面能接的数更多)，那么在LIS长度相同时，我们保留最小的ai

动态的维护最小LIS的结尾

那么即得到下图：

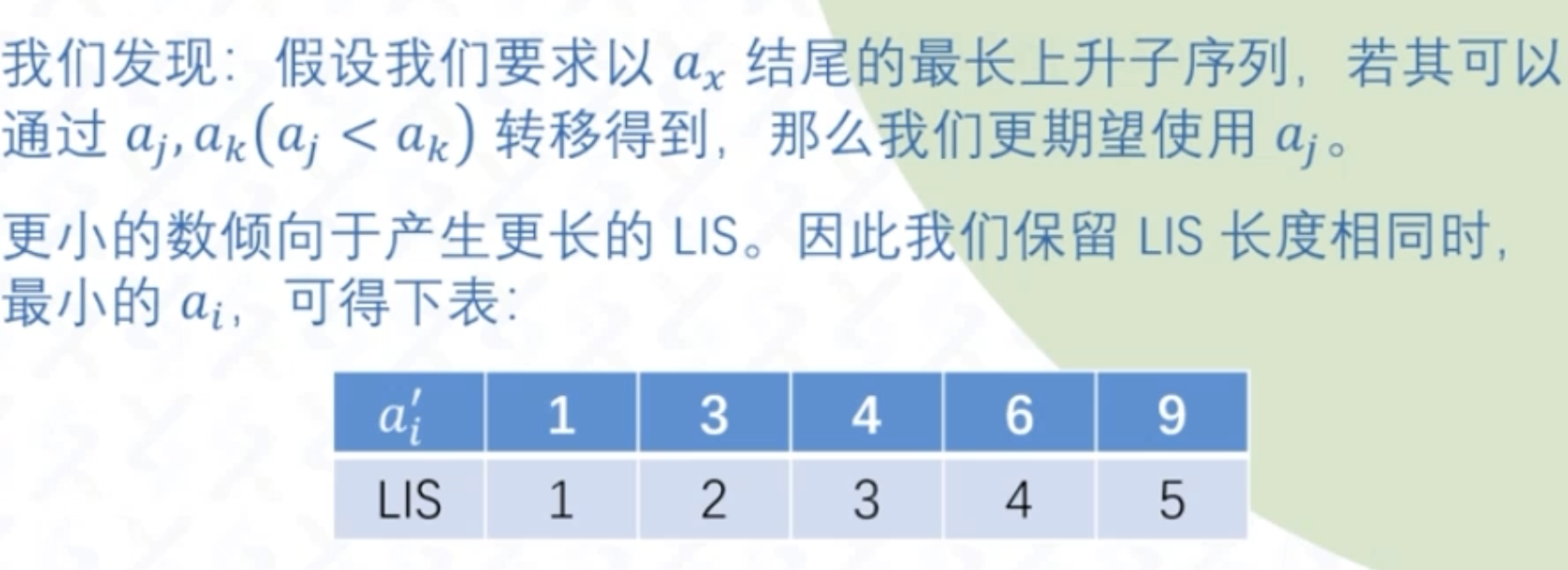
此时当后面接7时，即将LIS5的9替换掉(更优)，读2换3，读8则接到后面使LIS长度+1

LIS存在着单调性：当x<a'len(len为LIS长度)则替换，否则加入队尾

有着明显单调性，则这两个操作可以通过二分来实现

for(int i = 1; i <= n; ++ i) {
    //找第一个大于等于a[i]元素
    int pos = lower_bound(g + 1, g + len + 1, a[i]) - g;
    g[pos] = a[i];//将此为改为a[i]
    len = max(len, pos);//更新长度
}

二维DP

数字三角形，二维通过(i, j)两个数来确定位置

LCS：
对于LCS的两个序列，无法用一维来定位，二维：定义为f[i][j]表示为数列A的前i位与数列B的前j位组成的LCS
此时有情况：

• 匹配：长度+1
• 不匹配：从前面长的过渡过来
  

再看LCS：重标号构造单调递增
发现若数列A，B为同列(1～n都各出现一次)，则有对序列重标号，此时局面为求一序列与另一单调递增序列求LCS，那么就是求序列中的最长LIS即可

其中32145为abcde，12345为cbade
那么因为单调递增，求另一个最长ade，一定可以再单调序列取到

即当1～n都出现一次，则可转换为求LIS问题，在套用前面nlogn求LIS
但存在强限制：AB都为数列，但很多时AB都为字符串

编辑距离：P2758 编辑距离
两维，f[i][j]表示A的前i个字符变为B的前j个字符的最小操作次数，因此当为f[n][m]时则为A的前n个字符=B的前j个字符

对于三种操作：

• 删除：f[i][j] = f[i - 1][j] + 1

即不要第i个字符

• 插入：f[i][j] = f[i][j - 1] + 1

同理

• 修改：f[i][j] = f[i - 1][j - 1] + [Ai != Bi]

将A的前i-1变为B的前j-1字符，再加上是否相等的修改(不想等则+1次操作)

#include <bits/stdc++.h>
using namespace std;
int min(int x, int y, int z) {
    return min(min(x, y), z);
}
int edit_dist_dp(string str1, string str2) {
    int m = str1.length();
    int n = str2.length();
    vector<vector<int>> dp(m + 1, vector<int> (n + 1));
    for(int i = 0; i <= m; ++ i) {
        for(int j = 0; j <= n; ++ j) {
            if(i == 0) {
                dp[i][j] = j;//当A中字符数为0，要插入j次来构造j
            }
            else if(j == 0) {//当B中字符为0，A要删除j次来构造j
                dp[i][j] = i;
            }
            else if(str1[i - 1] == str2[j - 1]) {//A=B直接转移，不操作
                dp[i][j] = dp[i - 1][j - 1];
            }
            else {//否则计算最小操作步数
                dp[i][j] = 1 + min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]);
            }
        }
    }
    return dp[m][n];
}

int main() {
    string str1, str2;
    cin >> str1 >> str2;
    cout << "Mininum number of operation:" << edit_dist_dp(str1, str2) << endl;
    return 0;
}