树&图(vector自带size函数)

树：除根节点，每个节点只有一个父节点

存在层级和高度，具有递归性

树性质：all结点连通，无环，一个n个结点树，有n-1条边

二叉树：每个节点最多只有两个子节点

• 完美(满)二叉树：除最后一层外每个节点都拥有2个子节点，因此一个n层满二叉树，节点个数为2^{n-1个，叶子节点个数为2}(n-1)个
• 完全二叉树：all结点都从左到右排下

对于完全二叉树中某结点a：有a的左子节点为2a，右子节点为2a+1，它的父节点为a/2(下取整)
(0开始)第i层节点数为2^i

二叉树存储：

• 同上方(连续编号)：对于n层二叉树，数组空间大小为最右边叶子节点的编号，即2^(n-1)+1

但对于n=20几时，所占用空间即爆炸

• 结构体存储：空间上只开到n

二叉树深度：即分别递归求左右子树高度+1(我的儿子到我)，即最大深度

二叉树遍历

分为BFS层次遍历，DFS遍历

先：根左右
中：左根右
后：左右根

前序中序转后序：知前，中序，建立形态即可得出它的后序

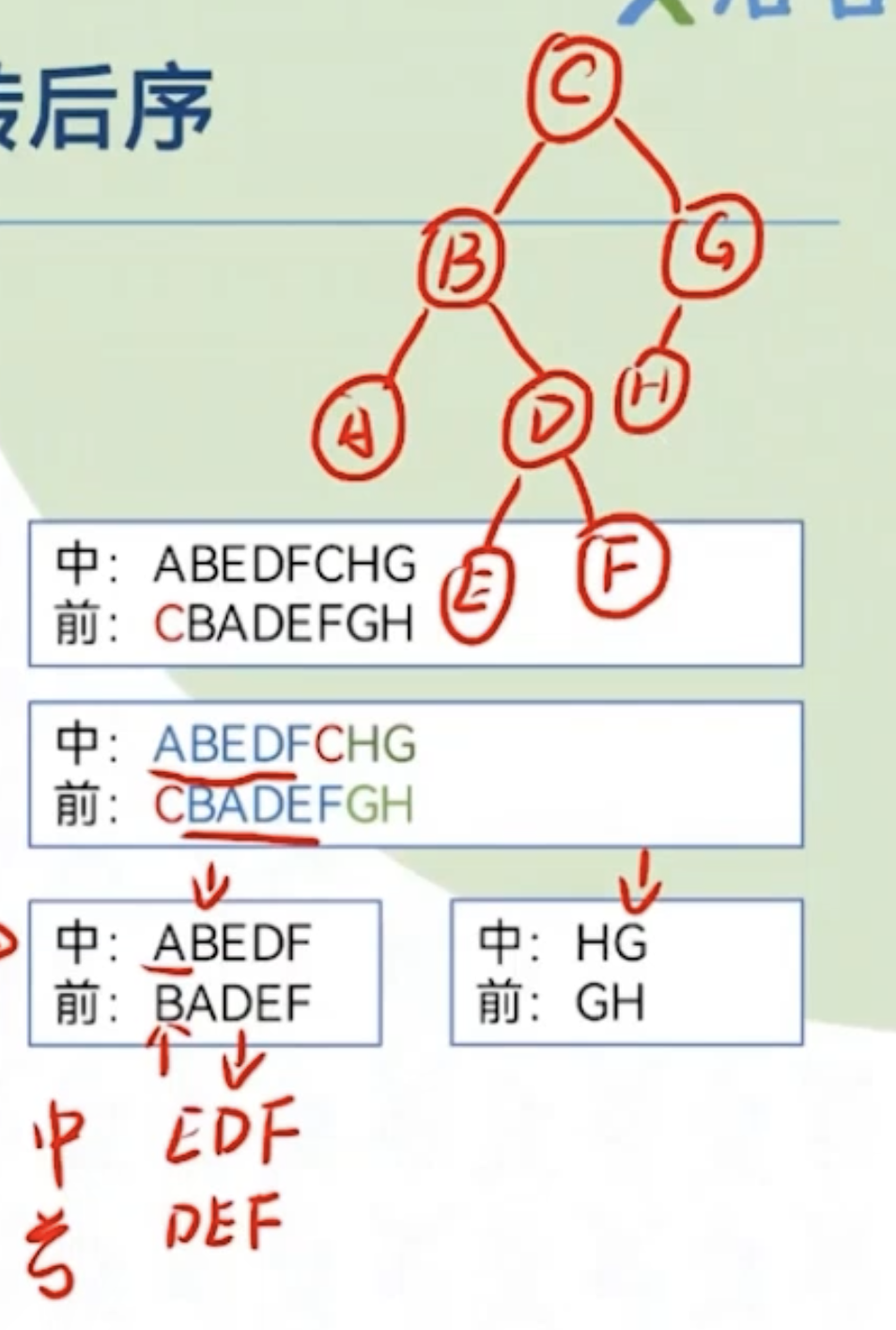
通过前序和中序不断分割原树建立原树

根据前序遍历先根的特性，我们知道对于当前根为C，又因为中序左根右的特性，我们可以得到C左边是C的左子树，C右边是C的右子树
(不断重复)即建立原树

点击查看代码

int build(int l1, int r1, int l2, int r2) {//l1和r1为前序，l2和r2为中序
    if (l1 > r1 || l2 > r2) return 0;
    int r = a[l1];
    for(int i = l2; i <= r2; ++ i) {//分割左右子树
        if(b[i] == a[l1]) {
            t[r].l = build(l1 + 1, l1 + i - l2, l2, i - 1);
            t[r].r = build(l1 + i - l2 + 1, r1, i + 1, r2);
            break;
        }    
    }
    return r;
}

其中i-l2是中序中左子树结点数，去对应的先后序中加法即可

中后转先

int build(int l1, int r1, int l2, int r2) {
    int r = a[r1];
    if(l1 > r1 || l2 > r2) return 0;
    for(int i = l2; i <= r2; ++ i) {
        if(b[i] == a[r1]) {
            t[r].l = build(l1, l1 + i - l2 - 1, l2, i - 1);
            t[r].r = build(l1 + i - l2, r1 - 1, i + 1, r2);
            break;
        }
    }
    return r;
}

图：图是点，边的集合

也分为有向图和无向图(双向)，对于无向图度数又可以分为出度和入度
图包括：不连通图，有向无环图DAG，环，链等，包括树也是图的一种：有根树，无根树，森林等

度数：顶点连边的数量
重边：两点间不止一条边
自环：连像自己边
类似的还有边权，点权

对于图G = (V, E)，其中V为点的集合，E为图中边的集合

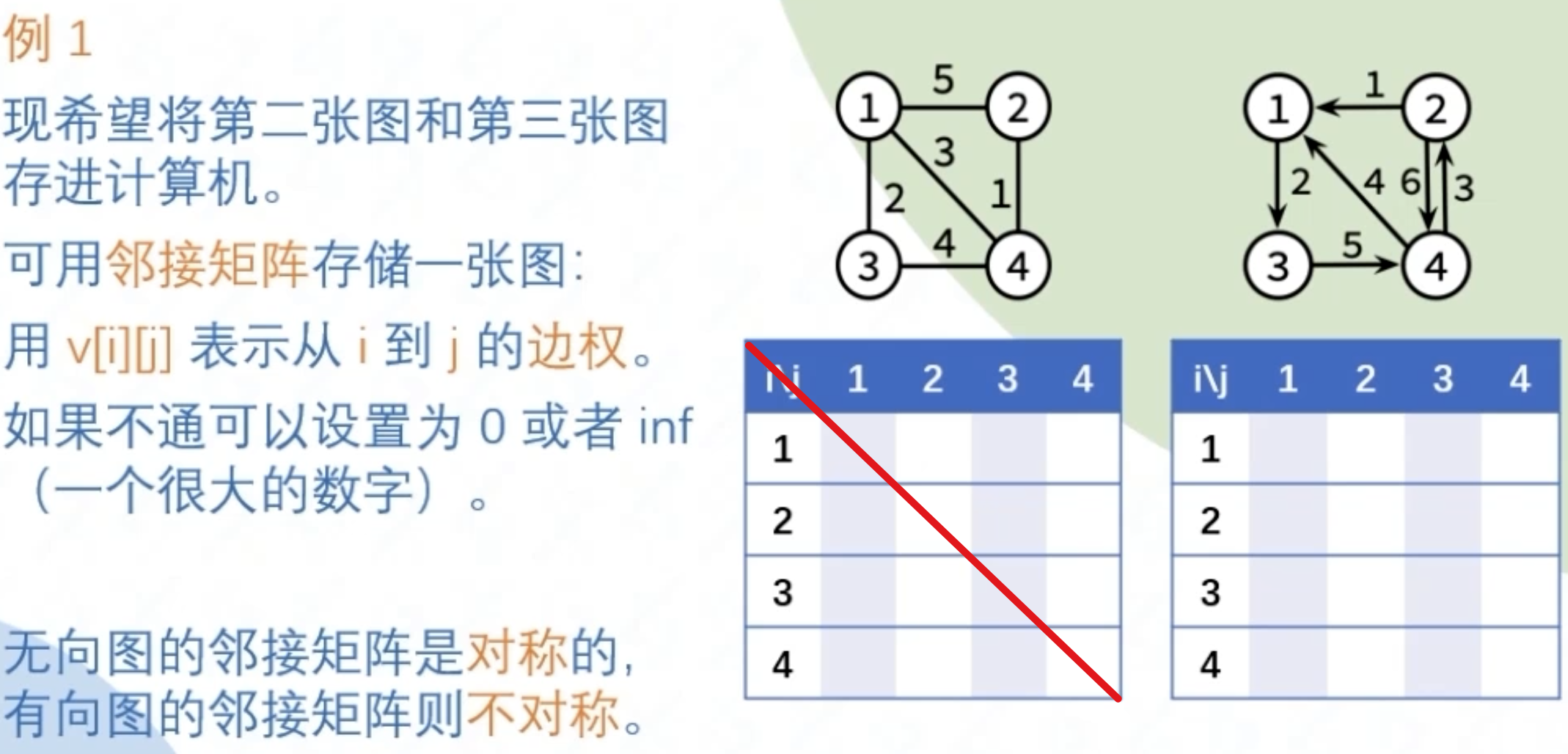
图存储：多维矩阵

适用条件：邻接矩阵适用稠密图(点多)，邻接表适用稀疏图(边多，特别是重边边权不同时)

• 邻接矩阵(二维数组)：v[i][j]记录i到j的边权

其中对角线全为0，无法自己连向自己

对于一个n点m边的邻接矩阵大小为n*n(即只与点数有关)，那么对于它的遍历也是n^2级别的

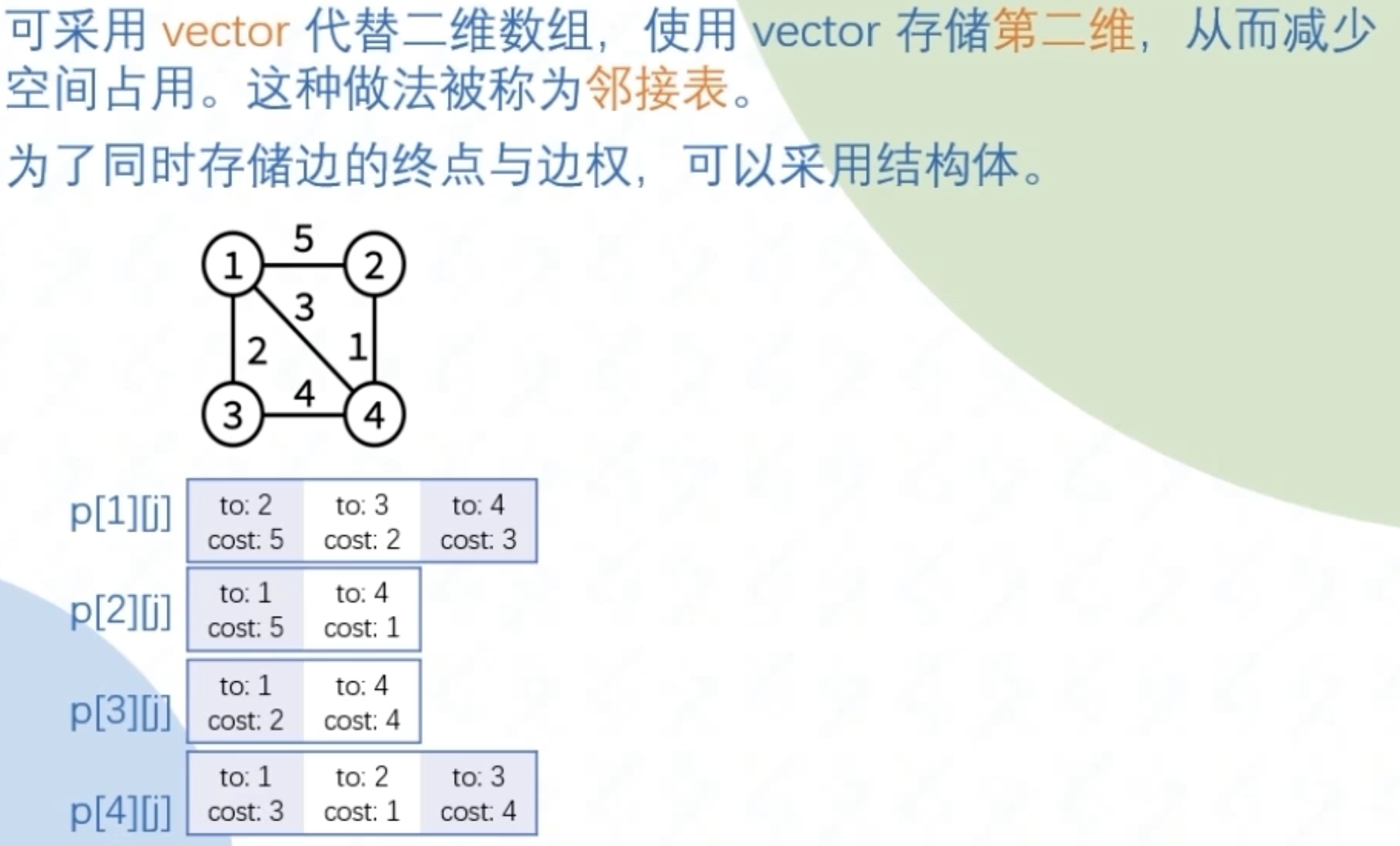
• 邻接表(根据q[i].size()来限制下层合法空间)：采用vector代替二维数组，vector存储第二维

空间为m即边数，遍历点的时复为p(p为点的出度)，缺点是对于修改ij的边权为Op，而不是邻接矩阵的O1

邻接表排序按顺序

for(int i = 1; i <= n; ++ i) {
  sort(q[i].begin(), q[i].end());
}

两种方式互相转化：其中vector从下标0开始

图的遍历：图上跑DFS和BFS + 访问数组

依次通过q[u][i]去跑，dfs(u)为root结点，再用依次跑儿子结点，bfs(u)同理

在使用邻接表情况下时复为O(n+m)

点击查看代码

void dfs(int x) {
    // if(x == 0) return ;//不需要边界是因为图上dfs只会跑存在的点，不存在是不会遍历到的
    cout << x << ' ';
    for(int i = 0, sz = q[x].size(); i < sz; ++ i) {
        if(!u[q[x][i]]) {
            u[q[x][i]] = 1;
            dfs(q[x][i]);
        }   
    }
}

void bfs(int x) {
    u[x] = 1;
    p.push(x);
    
    while(!p.empty()) {
        int tmp = p.front();
        cout << tmp << ' ';
        p.pop();
        for(int i = 0, sz = q[tmp].size(); i < sz; ++ i) {
            if(!u[q[tmp][i]]) {
                u[q[tmp][i]] = 1;
                p.push(q[tmp][i]);
            }
        }
    }
}

反向边：对于退化为链的情况跑每个点到达的最大编号会跑n^2级别，对每个点建立反向边(未遍历则更新为最大值)，这样只需要m次

即枚举最大的点能到哪些点

对于占位数组和数值数组的优化，当a[q[x][i]] == 0可以认为无占位，合二为一

重边和自环处理：发现即使一个点被标记走过，但我能走到这个点，那么路径一定是我 + 1(1步走到)，那么此时有两种情况：

• 最短 = 我 + 1：那么说明此时存在一条重边，即使它被更新过，也处理
• 最短 < 我 + 1：说明往回走了，不更新

for(int i = 0; i < q[x].size(); ++ i) {
	int t = q[x][i];
	if(!vis[t]) {//可到点，标记走过
	vis[t] = 1;
	d[t] = d[x] + 1;
	p.push(t);
	}
	if(d[t] == d[x] + 1) {//处理走过的写法
	f[t] = (f[t] + f[x]) % mod;
	}
}