背包问题：选or不选，选多少

背包

NC16693简化01
对于前面物品(a+b=c+d+e)方案，后面不关心其结果是如何来的，关注的是箱子空间剩多大

关心对于箱子容量提供剩余的可能性

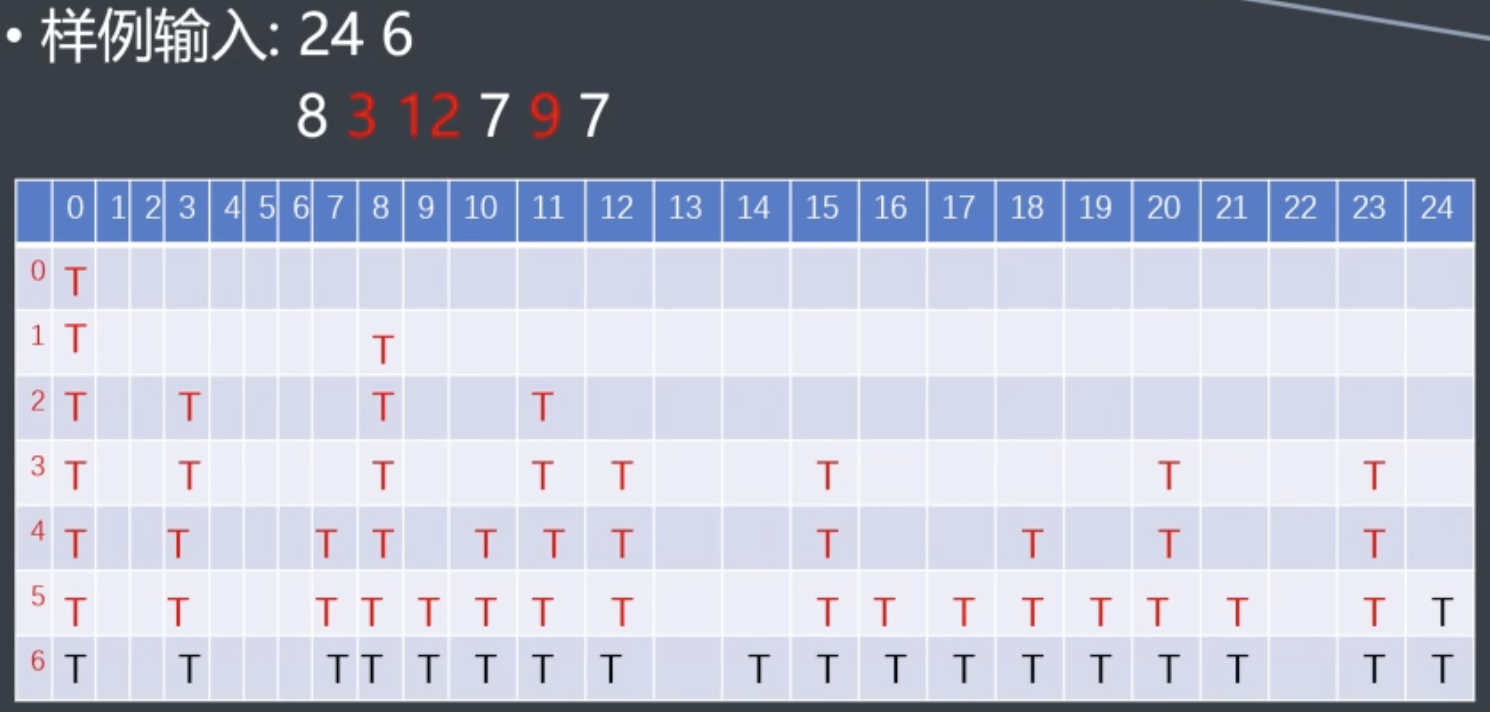
即对于{2,2,4,6}->一共可能即2，4，6，8，10，12，14的可能性，对于暴力2^4(明显没必要)
那么，枚举最后一个物品放or不放：f[i][j] = f[i - 1][j] (前i-1物品已经可以装满，此时放or不放第i个物品一样)｜f[i - 1][j - v[i]] (塞满体积为v，最后一个物品v[i]，看i-1能否放j-v[i]的体积)

for(int i = 1; i <= n; ++ i)
        for(int j = 0; j <= v; ++ j)

其中j体积要从0开始而不是v[i]：因为存在小于v[i]继承于i-1层情况的情况，j从v[i]开始循环回丢失这部分

0/1滚动数组：

点击查看代码

``` #include using namespace std; int v, n, a[40], f[2][20020]; int main() { scanf("%d%d", &v, &n); for(int i = 1; i <= n; ++ i) { scanf("%d", &a[i]); } memset(f, 0, sizeof(f)); f[0][0] = 1; for(int i = 1; i <= n; ++ i) { for(int j = 0; j <= v; ++ j) { if(j >= a[i]) { f[i % 2][j] = f[(i - 1) % 2][j] || f[(i - 1) % 2][j - a[i]]; } else f[i % 2][j] = f[(i - 1) % 2][j]; } } int ans = 0; for(int i = v; i >= 0; -- i) { if(f[n % 2][i]) { ans = i; break; } } cout << v - ans << endl; return 0; } ```

自我滚动：存在多次重复使用造就假合法问题

出现顺序问题，即对于状态可能多次采用已经放置的物品的基础上再次执行(无法分清状态是上一层而来还是本层)，那么即要将其隔离

采用从后往前更新，即保证了后续更新不会用到已经更新的值

标准01：每件1个
类似的对于同样的放了x的体积的方案不关心具体放了哪些，在x基础上考虑加入or不加入当前物品得到的结果y即可

定义：前i个物品恰好放满j体积得到的价值

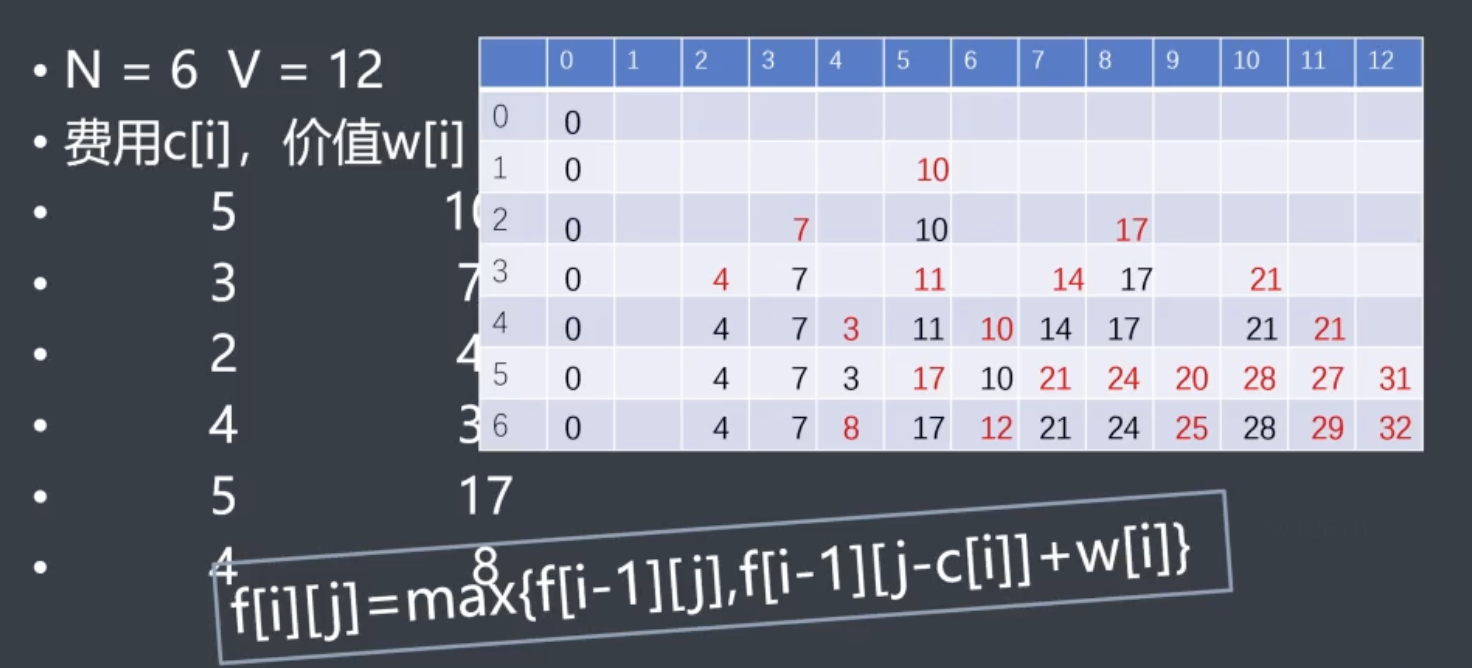
为防止影响将all值初值赋为-INF，最终结果扫一遍f[n][1～m]找到最大值

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1010, INF = 1e9;
int w[N], v[N], f[N][N], ans;//f[i][j]：前i个物品，恰好装满体积j的最大价值
int main() {
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];

    for (int i = 0; i <= n; ++i)
        for (int j = 0; j <= V; ++j)
            f[i][j] = -INF;
    f[0][0] = 0;//装0体积价值为0

    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j <= V; ++j) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i] && f[i - 1][j - v[i]] != -INF)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }
    for (int j = 0; j <= V; ++ j) ans = max(ans, f[n][j]);//取最大值
    cout << ans << endl;
    return 0;
}

对于无需扫描版本(将初值赋为0)：有同样定义，但思路上是采用了：
(一个$\forall 体积$)虚拟物品 + 当前实际物品体积 = $背包_{MAX容量}$的策略

致使本层更新时保证选择更优的价值来作为当前价值

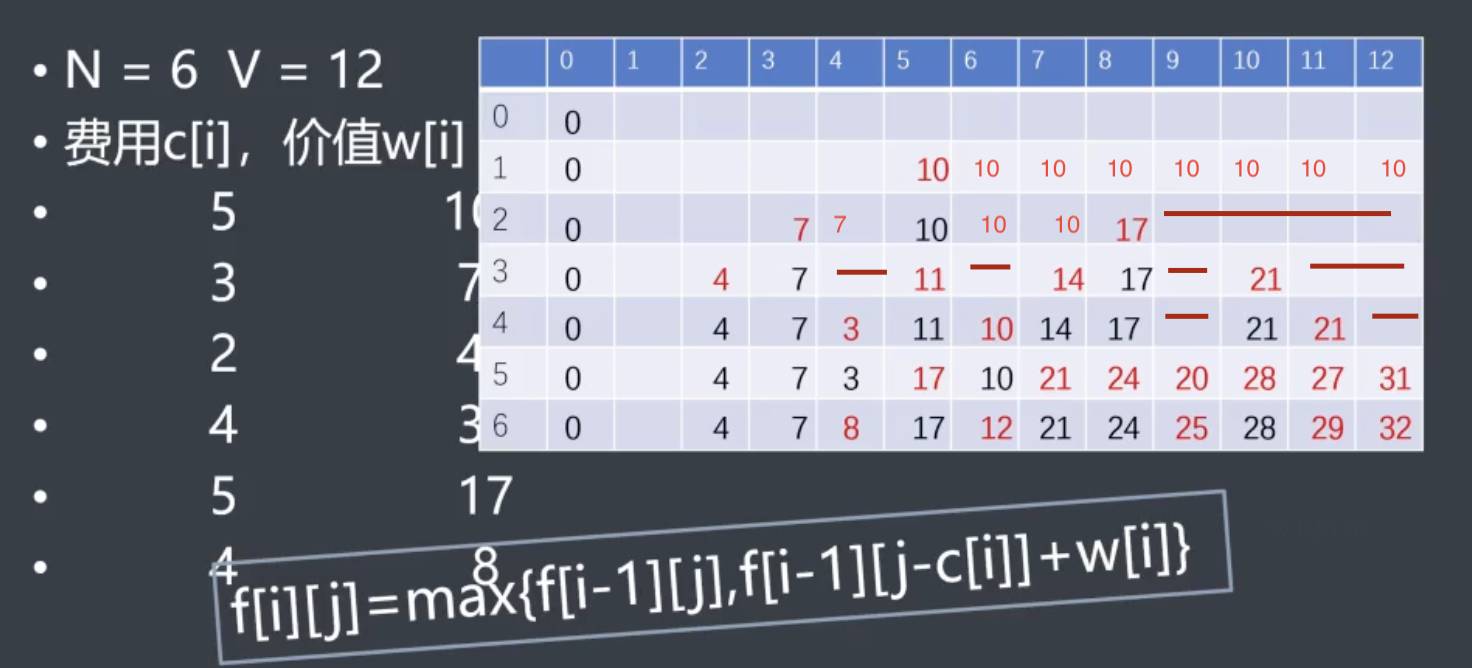
但对于题目要求恰好为塞满j体积，则无法置入虚拟物品占位，仍需采用-INF赋值+扫描方法

for(int i = 1; i <= n; ++ i) {
    for(int j = m; j >= a[i]; -- j) {
        if(f[j - a[i]] + w[i] > f[j]) {
            f[j] = f[j - a[i]] + w[i];
        }
    }
}

记忆化：

点击查看代码

#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N], w[N], v[N];//v体积，w价值，fij为all状态 
int n, m;
int solve(int i, int j) {
    if(f[i][j]) return f[i][j];
    if(i == 0) return 0;
    int res;
    if(v[i] > j) res = solve(i - 1, j);
    else res = max(solve(i - 1, j), solve(i - 1, j - v[i]) + w[i]);
    return f[i][j] = res;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    cout << solve(n, m) << endl;
    return 0;
}

扩展(数据范围来看)

N=20，v<1e9：体积过大-> $2^{20}$爆搜all物品选/不选
N=40，v<1e9：恰好有20基础上翻倍->分为两部分折半搜索，然后对两部分进行拼接
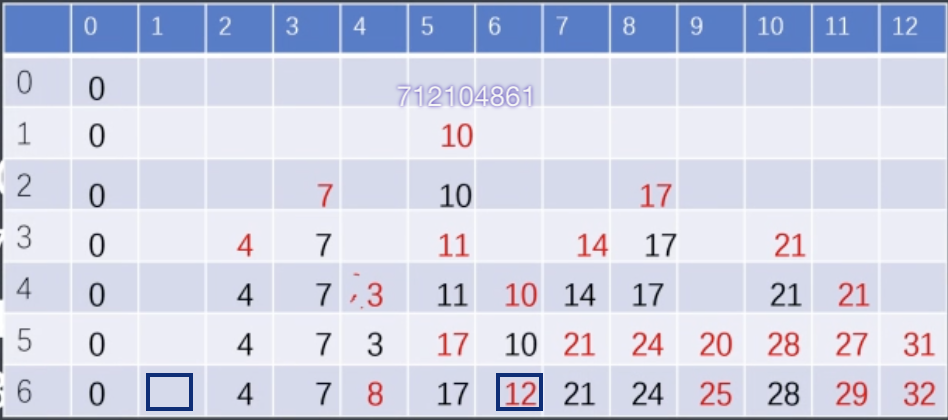
N=100，v<1e9：采用离散形式保留有可能成为答案的体积对应的最大价值
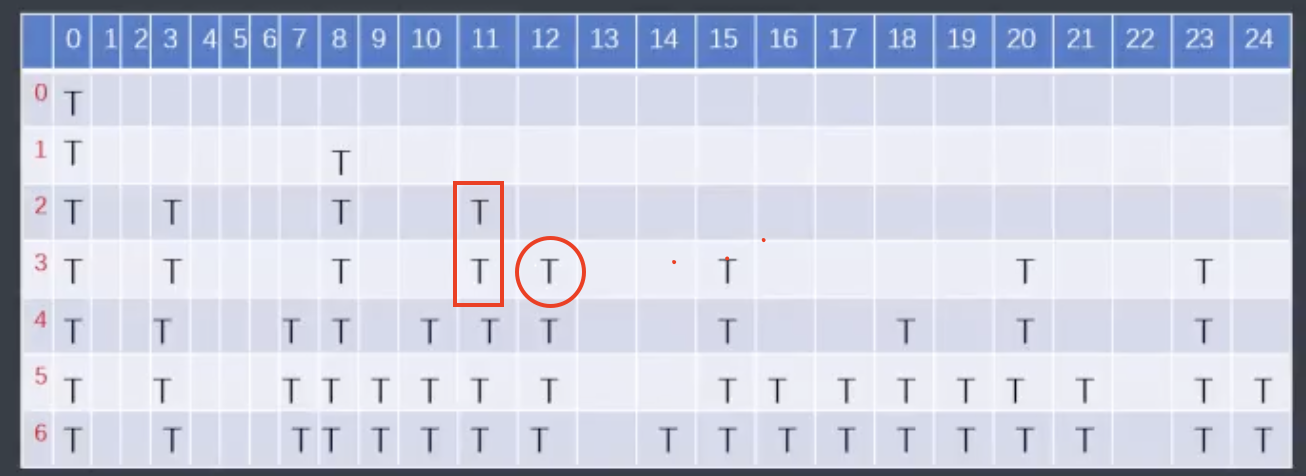
分析发现对于某些位置(其本身不存在or非最优)，不会成为答案
e.g.如图中[]和12(虽然存在但<前面1的值17)

类似的这些点显然是不必要的

(同理)当n扩大时，存在许多这种的冗余:
(1)无法组成此体积
(2)恰好拼成当前体积价值<恰好拼成小于当前体积的价值

处理方式是用map代替数组(过滤数据，选择性的存储)：map<下标，值>，保证下标递增时值递增

此时不断转移，使得不断填空间的一个过程

完全背包：每个物品有♾️个
即要考虑第i个物品放了k件(0 <= k * v[i] <= m)，这样的时复为O($V*\sum_{}^{}\frac{V_{体积}}{v_{当前物品}} $)

这里发现对于0/1自我滚动：顺序会导致物品被重复使用(刚好适用当前场景)

更新后续状态时取最优前置状态不断更新后续的过程保证了循环k

for(int i = 1; i <= n; ++ i)
    for(int j = 0; j <= m; ++ j)
        for(int k = 0; k * v[i] <= j; ++ k)//核心操作：对第i个物品选择了k个
            f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

对于更新同一层状态的多次转移来说，保证了当前状态为最优状态(以此来优化k)

多重背包：每件物品有x个
朴素想法是同完全背包，k(0<= k * v[i] <= m(这里m是物品限制数量))，O($V*\sum_{}^{}v_{当前物品}$ )

考虑问题转化：

0/1转化：若将每个物品k个拆开视为单独不同的物品(数量相同)，但未改变复杂度

想将原本m件物品拆分(打包)出物品的数量x(x < m)，又要x可以通过某种组合来拼出原区间，即满足

x通过组合可以凑出m
$x_{max组合} < 7$

发现刚好满足二进制拆分形式$(m)_2$，再根据组合(子集)的思路进行处理，有$(\sum_{0}^{b}2^b) + 剩余值a$ = m

m = 8 拆为 -> 1，2，4，1，max组合为8

e.g.对于22，拆分为1，2，4，8，7
有{1，2，4，8}组合表示出< $2^k-1$的数(1~15)，对于剩余15～22显然可以通过再取一个< $2^k-1$来凑出(相当于在值为m-$2^k-1$ = 7 基础上加上一个<$2^k-1$数)来凑得后续数

方法：
将第i种物品分成若干件物品，每件物品有一个系数，这种物品的费用和价值均是原来的费用和价值乘以这个系数
系数为1，2，4，···，$2^{k-1}$，ci-$2^{k+1}$，且k满足c[i]-$2^{k+1}$>0的最大整数

例如n = 13，物品分成系数分别为1, 2, 4, 6四件物品

时复为O($V*\sum_{}^{}\log_{}c[i](第i种物品数)$)

点击查看代码

#include <iostream>
#include <algorithm>

using namespace std;
//物品个数最多为1000*log2000(上取整)大约12，所以1000*12大约240000，这里开250000
const int N=25000,M=2010;

int f[M];
int n,m;
int v[N],w[N];
 
int main()//01背包可用1维优化，这里直接写1维
{
    cin>>n>>m;
    int cnt=0;//存all新物品编号
    for(int i=1;i<=n;++i)
    {   
        int a,b,s;//读入当前物品体积，价值，个数
        cin>>a>>b>>s;
        int k=1;//从1开始分
        while(k<=s)//有k<=s则可以分
        {          //每次将k个第i个物品打包在一起
            cnt++;//当前新物品编号++
            v[cnt]=a*k;//v[cnt] = k个物品打包在一起，体积即a*k
            w[cnt]=b*k;//价值即b*k
            s-=k;//算好k，讲k从s中减去
            k*=2;//每次k*2
        }
        if(s>0)//最后若s>0，则说明还剩下一些数要补上
        {//此时剩下s的最后的c，补上即可
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    n=cnt;//最后将n更新为cnt，做一遍01背包即可
    for(int i=1;i<=n;++i)
        for(int j=m;j>=v[i];--j)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[m]<<endl;
    return 0;
}

单调队列优化：

点击查看代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 20010;
int n,m;
int q[N], g[N], f[N];
int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; ++ i)
    {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);//滚动数组记录上一层
        for(int j = 0; j < v; ++ j)//枚举余数
        {
            int hh = 0, tt = -1;//定义单调队列
            for(int k = j; k <= m; k += v)
            {
                if(hh <= tt && q[hh] < k - s * v) ++ hh;//是否滑出窗口
                if(hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);//队列不空，求窗口内部
                while(hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) -- tt;//将没有用元素弹出
                q[++ tt] = k;
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

二维费用背包
即对于新增的Weight(类似V)，同V处理方式新增一维即可

定义：f[i][v][u]为在前i种物品中选，付出两种代价v和u时获得的最大价值
转移方程：f[i][v][u] = max(f[i][v][u]，f[i][v - a[i]][u - b[i]] + w[i]);

当题目出现更多的限制时，即考虑更高维的状态定义即可

点击查看代码

#include <iostream>
using namespace std;
const int N=110;
int n,V,M;
int f[N][N];
int main()
{
    cin >> n >> V >> M;
    for(int i = 0; i < n; ++ i)
    {
        int v, m, w;
        cin >> v >> m >> w;
        for(int j = V; j >= v; -- j)
            for(int k = M; k >= m; -- k)
            f[j][k] = max(f[j][k],f[j - v][k - m] + w);
    }
    cout << f[V][M] << endl;
    return 0;
}

分组背包
显然对于组内的决策(选哪个)对答案有影响，前面选的会影响后续决策(不符合DP无后效行)，此时需要更换决策按每组去看(而非按每个去看)

定义：f[k][v]为前k组物品花费费用v获得的最大权值

forijk保证每组最多选1个物品

若将fori，j，k顺序改为fori，k，j则等价于<=>0/1背包(物品不受同组限制)

对于i，k，j：可能导致对于第x组物品$x_i$放入之后又有$x_{i+k}$基于$x_i$状态继续放入(叠加)

可能在第x组选了一些的情况下，继续选择然后放入

可能就会退化为0/1背包，一定有建立在当前组未作出选择的状态下进行更新

对于i，j，k：有对于第i组的x组物品之间存在竞争关系

点击查看代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int v[N][N], w[N][N], s[N];
int f[N][N];
int n, m;
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; ++ j)
        cin >> v[i][j] >> w[i][j];
    }
    for(int i = 1; i <= n; ++ i) {//group
        for(int j = 0; j <= m; ++ j) {
            f[i][j] = f[i-1][j]; // 不选当前组的任何物品
            for(int k = 1; k <= s[i]; ++ k) {
                if(j >= v[i][k]) {
                f[i][j] = max(f[i][j], f[i-1][j-v[i][k]] + w[i][k]);
            }
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

自我滚动：

点击查看代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int v[N][N], w[N][N], s[N];
int n, m;
int f[N];
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i)
    {
        cin >> s[i];
        for(int j = 0; j < s[i]; ++ j)
        cin >> v[i][j] >> w[i][j];
    }
    for(int i = 1;i <= n; ++ i)
        for(int j = m; j >= 0; -- j)
            for(int k = 0; k < s[i]; ++ k)
            if(v[i][k] <= j)
            f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m] << endl;
    return 0;
}

posted on 2025-05-14 21:42 TBeauty 阅读(251) 评论(0) 收藏举报

刷新页面返回顶部

OVSolitario-io

导航

公告

背包问题：选or不选，选多少