DP(表格法):相同子问题+最优子结构,状态包含all的历史信息 + 特判
起手局面
DP适用情况:满足
- 相同子问题
在各个阶段中拥有相同子问题,对于i层决策时,默认我的前i-1~1层已经最优,所以关注于本层逻辑实现即可
- 最优子结构:最优解推最优解
最优证明及来历为何为切入点:
最优<等价于> = 前置最优 + 本层最优
若想让整个问题最优,那么一定有我的前置最优+我本层得到最优
反证法:如果我的前置中的某一个并非最优,那么一定有将它更改为最优后,使得我的前置最优
所以当我的前置最优时,只要考虑我最优的情况即可构造出最优
本层一定有从上一个阶段最优推得,若后续影响改变前面阶段的比重,那么就无法使用DP解决
无后效性:当前决策与历史决策无关
e.g.走楼梯+(走过50阶楼梯则无法走100阶)限制,那么此时f[i]仅表示从起点走到i方案数,未体现是否走过x,那么即加上是否走过x,f[i][0/1] (0走过,1没走过)
分情况讨论50~100之间没走过50阶f[i][0]和走过f[i][1]
算法思路: 暴力 + 对其瓶颈的优化
DP:发现原问题可以转化为几个小问题,通过解决小问题即可解决原问题,以此为基础设计表格
DP是表格法
设计表格(可能是多维),然后不断填表的过程,用已知填未知,这个表格可能不一定为一维线性,对于数字三角形表格则呈现三角形形状
将大问题拆分为小问题,再通过小问题的解来解决当前问题(切入点是状态的来历)
考虑all来历,取最优即可
DP原理: 其应用加法原理和乘法原理

取每步最优则可将mn降低为n
DP核心是状态的定义和状态的计算,好的状态定义再根据由来和去处考虑出对应的状态计算方程
输出策略方案:即搜索记录我上一步是谁
状态定义:
从低维度到高维度考虑,需要哪些量,哪些就成为变量
最优证明及来历为何为切入点:
最优<等价于> = 前置最优 + 本层最优
若想让整个问题最优,那么一定有我的前置最优+我本层得到最优
反证法:如果我的前置中的某一个并非最优,那么一定有将它更改为最优后,使得我的前置最优
所以当我的前置最优时,只要考虑我最优的情况即可构造出最优
**为何来历作为切入点**:考虑来历重要的一点是我的来历到我的方式即状态转移的方式
那么此时DP即可看作一般的递推和递归问题
对于状态设计:明确的语意信息:即明确的f[a][b][c]代表什么
求什么设什么,在对细节方面进行修改:

本质:若f(n)能通过几个小的f()值得到,那么f()函数的设计是合适的
对于状态设计(是否合适):大问题的解无法通过小问题得到时,当状态设计无法分割为子问题时,或无法得知他的来历时,他是不那么好的
DP基本手段(用已有不断完成子问题)
对于问题n,解决几个更小规模问题,从而得到大问题的解
解决n转变为解决1,2···n
泛化问题,大问题的解通过小问题来解决,描述遇到小问题
状态转移:边界+由来去处
对于状态转移,一定保证历史清白的往下走

例子:DPe.g.
动态规划起源于数学博弈论其中的一部分,采用建表的方式计算,可以采用同样的思路,对于问题难点在于建表的过程(可能为多维表),然后去不断填表的过程
表格法练习:表格法练习
数字三角形
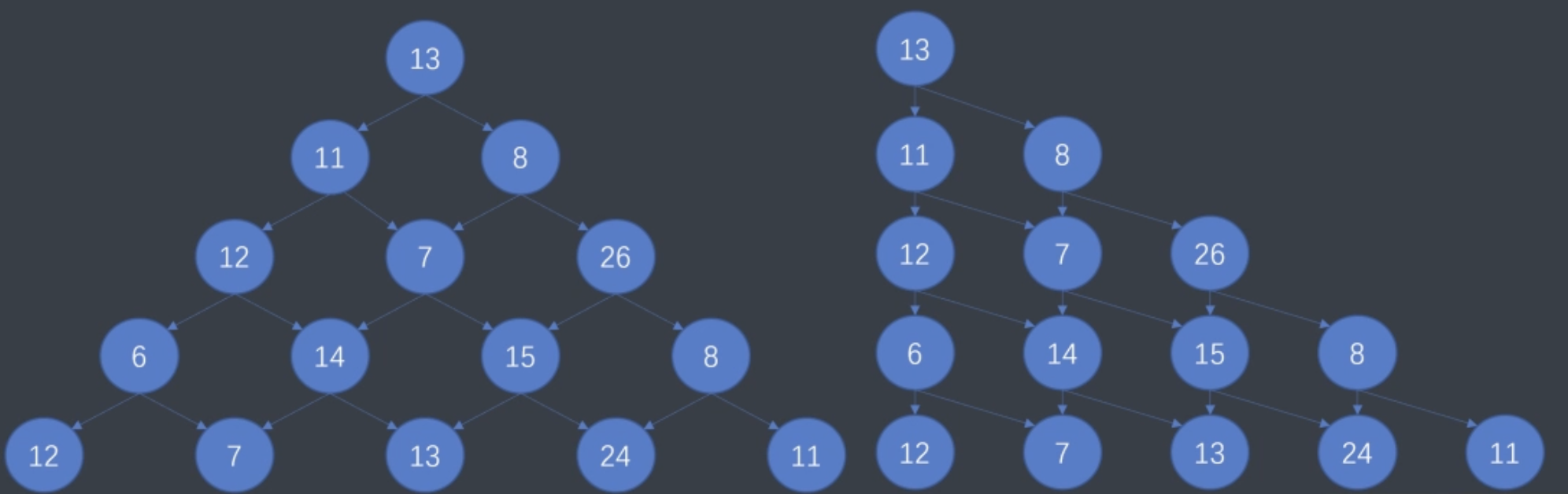
对于三角形,通过右移动转变为直角三角形形式建模,此时问题随机也转化为当前点,向下和向斜下走
表格法建立与填表:(值与对应的表)
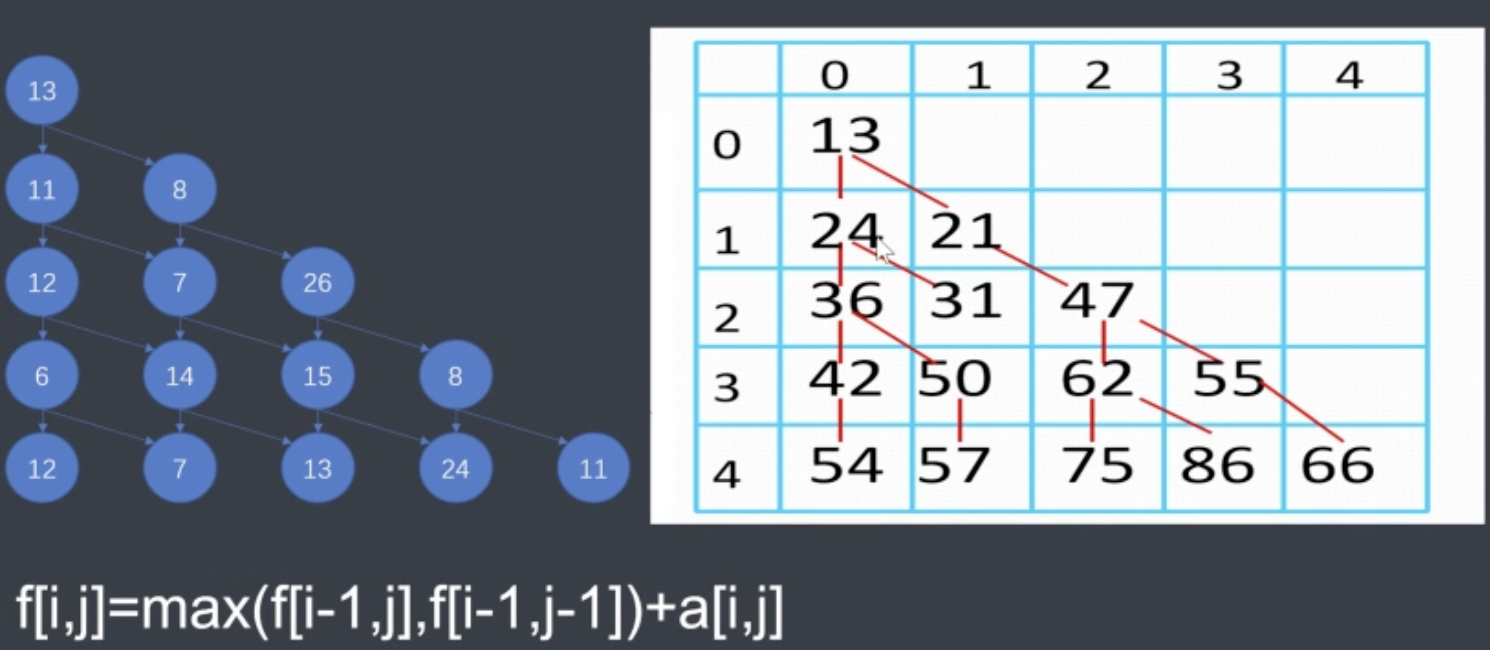
也可以倒叙,那么即剩遍历max,即1,1为最大值
其他内容:
拓扑排序:拓扑排序





 浙公网安备 33010602011771号
浙公网安备 33010602011771号