树与图

树与图

树与图的存储

树是一种特殊的图(无环连通图)，所以只考虑图即可

树和图有两种存储的方式:

1.有向图 ：边有方向

 

2.无向图：边无方向，可以从a走b，也可以b走a(算法中建一条a到b边，再建一条b到a边)

无向图是特殊的有向图

 

所以这里只考虑有向图

 

 

邻接矩阵：开一个二维数组g[a][b]存储a到b信息，如权重，a到b是否有边，但无法处理重边(但无影响，重边会保留最短的那条)，n^2(适合稠密图)

 

邻接表：即相当于开n个单链表(每个点开一个单链表，类似拉链法)，每个点单链表存这个点可以走到哪些点

 

如：有4个点，则开4个单链表，每个链表存对应点能到的all点(内部数序任意)

 

当想插入一个新的边2->3时，先找到2对应的单链表将3插入，(一般选表头)h[i]存的是第i个链表的链表头(插入方式同单链表插入)

 

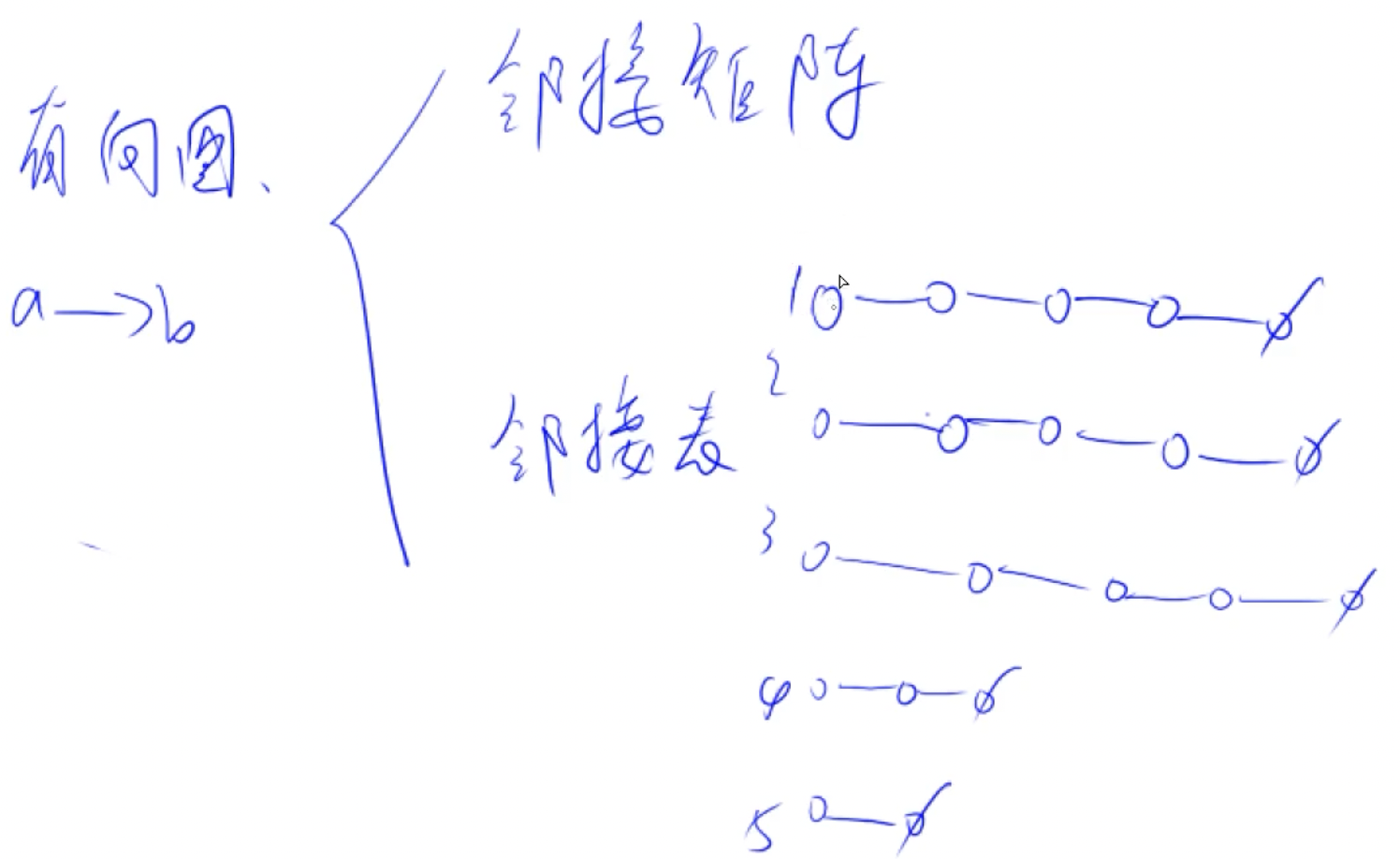
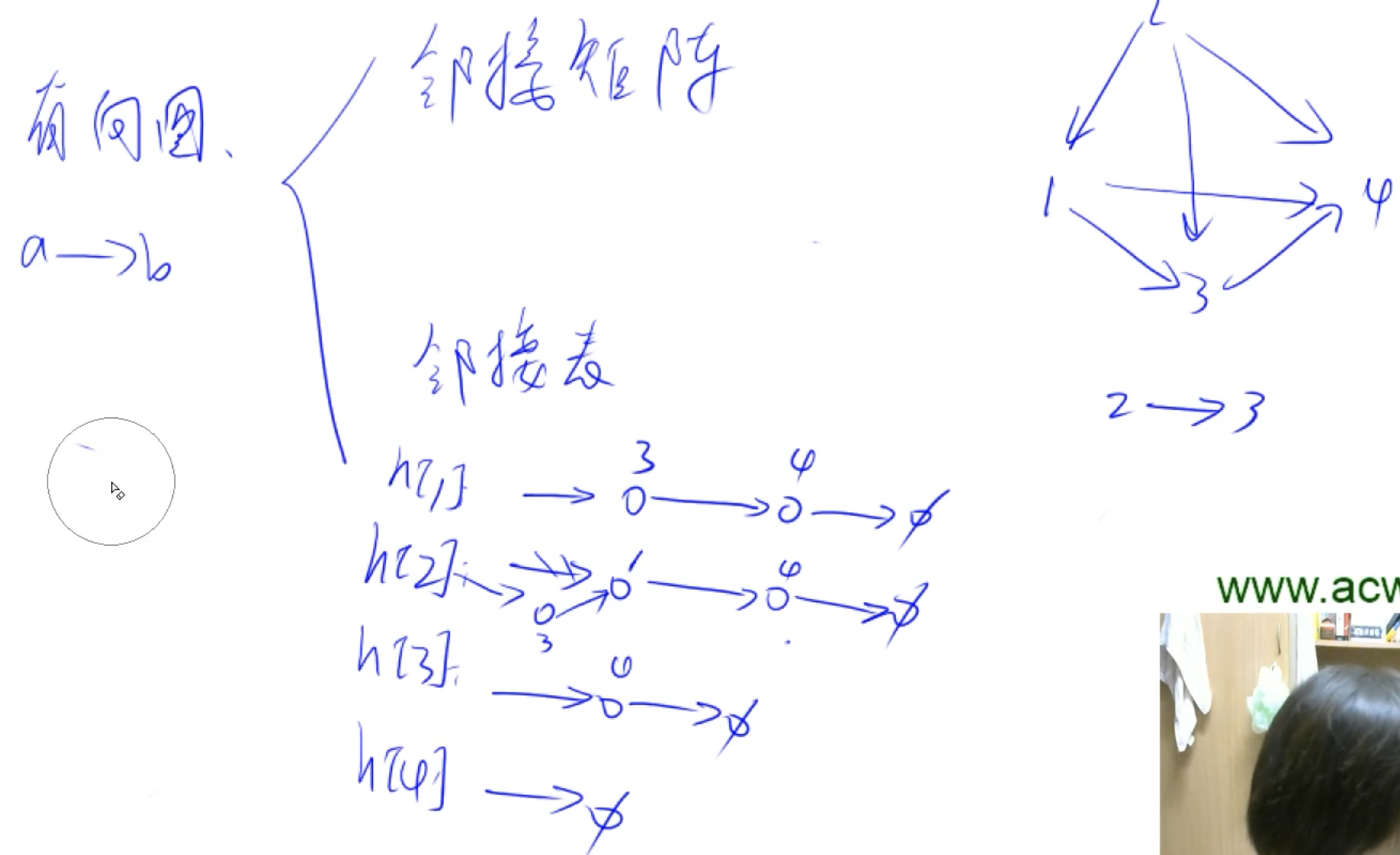
树和图的存储

#include <iostream>
#include <cstring>

using namespace std;

const int N=1e5+10,M=2*N;

int h[N],e[M],ne[M],idx;//此e，ne同单链表，之前有1个单链表所以head，这里n个单链表，所以n个头h[]

int n;
bool st[N];
int ans=N;

void add(int a,int b)//插入一条a指向b的边
{
    //插入一条边：即在a所在链表插入节点b
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int main()
{
    cin>>n;
    memset(h,-1,sizeof h);
    //邻接表初始化all头=-1即可
    //之前链表头节点指向-1，这里n个单链表都指向-1即可
    for(int i=0;i<n;++i)
    {
        int a,b;cin>>a>>b;
        add(a,b),add(b,a);
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

存邻接表可以用vector来存，但效率不如数组模拟

输入输出在100w才考虑用scanf，否则cin和scanf差不多

 

树和图的遍历

因为无向图也为特殊有向图，且树也是特殊的图，所以只考虑有向图如何遍历即可

 

图的深搜次序：一条路走到黑，走到7时回溯，走到8结束

 

图的宽搜次序：一层一层遍历

 

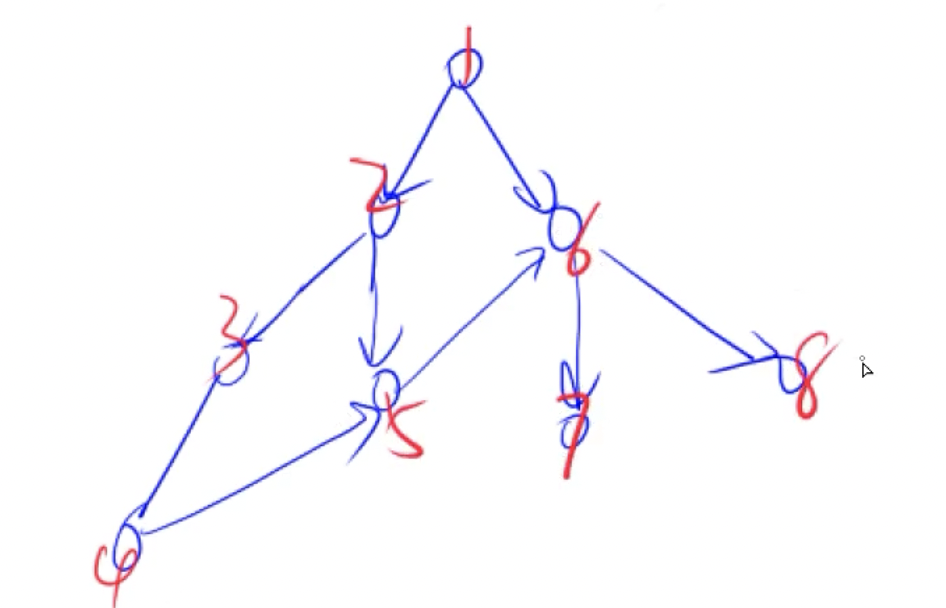
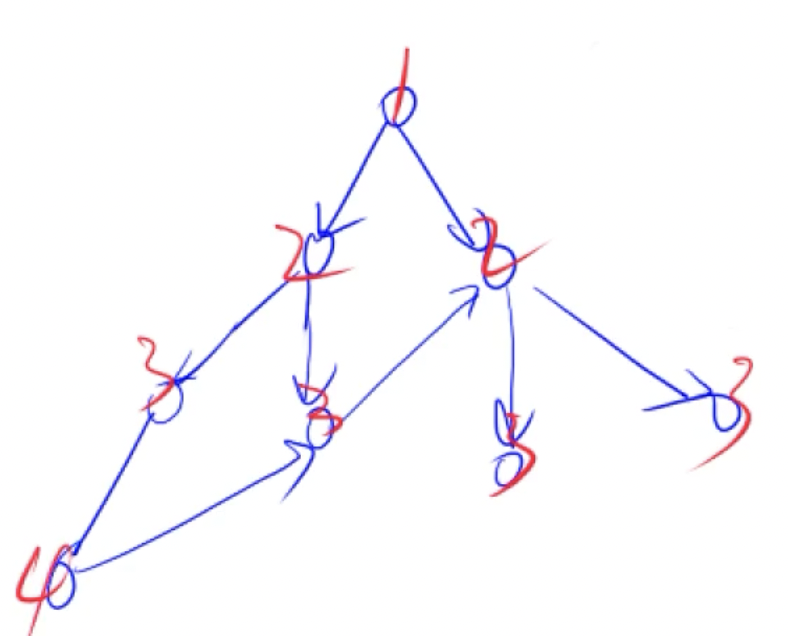
关于DFS和BFS一般每个点只遍历一次，可开个bool记录是否走过

 

树和图的深搜

#include <iostream>
#include <cstring>

using namespace std;

const int N=1e5+10,M=2*N;

int h[N],e[M],ne[M],idx;
int n;
bool st[N];
int ans=N;

void add(int a,int b)//插入一条a指向b的边
{
    //插入一条边：即在a所在链表插入节点b
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int dfs(int u)//u表示当前dfs到点
{
    st[u]=true;//标记当前点搜过
    //遍历u的all出边
    for(int i=h[u];i!=-1;i=ne[i])//同遍历单链表
    {
        int j=e[i];//当前节点在图中编号
        if(!st[j]) dfs(j);//j未被搜，则搜
    }
}

int main()
{
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=0;i<n;++i)
    {
        int a,b;cin>>a>>b;
        add(a,b),add(b,a);
    }
    dfs(1);//选任意点开始搜索
    cout<<ans<<endl;
    return 0;
}