回归分析-线性回归与逻辑回归
- 回归算法是一种通过最小化预测值与实际结果值之间的差距,而得到输入特征之间的最佳组合方式的一类算法。对于连续值预测有线性回归等,而对于离散值/类别预测,我们也可以把逻辑回归等也视作回归算法的一种。
- 线性回归主要用来解决连续值预测的问题,逻辑回归用来解决分类的问题,输出的属于某个类别的概率,工业界经常会用逻辑回归来做排序。
衡量回归算法是否成功:
- 方差:表示预测算法对所使用的训练集的敏感程度。(理想情况下,训练集的选择方式无关紧要,这意味着算法期望较低的方差)
-
偏差:表示预测算法对训练集上的假设的依赖程度。(做太多假设可能会使模型无法泛化,所以也应该选择低偏差)
线性回归
- 线性回归模型是探讨变量y和多个变量x1,x2,...,xn间的关系,用已有的训练数据为基础,总结问题本身的规律变化,并建立相应的回归模型来预测未知的样本数据。
- x(i)=(1,x1(i),x2(i),...,xn(i))和y(i)分别是第i个训练数据对应的自变量与因变量,回归函数:hθ(x)=θ0+θ1x1+θ2x2+...+θnxn=θTx
- 代价函数用来描述hθ(x)与对应的y的接近程度:

- 求代价函数最小值的方法:
- 最小二乘法:使用矩阵运算来求得θ,是对代价函数J(θ)求偏导并令其等于0。
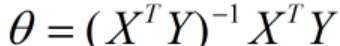
- 梯度下降法:要选取恰当的学习率α和多次迭代更新来求得最终结果
- 最小二乘法:使用矩阵运算来求得θ,是对代价函数J(θ)求偏导并令其等于0。
逻辑回归
- 逻辑回归是一个分类算法,它可以处理二元分类以及多元分类。
- 对于求得的Y 值是离散的,可以将Y做函数转换g(Y),函数g(Y)一般取为sigmoid函数,函数形式:g(z)=
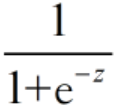 ,函数取值0~1,导数性质:
,函数取值0~1,导数性质: 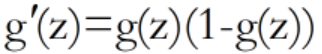
- 令z=xθ,h(x)=
 ,可以表示为某一分类的概率大小,y的概率分布函数表达式为:P(Y|X,θ)=h(x)y(1-h(x))1-y,用最大似然估计求解参数。
,可以表示为某一分类的概率大小,y的概率分布函数表达式为:P(Y|X,θ)=h(x)y(1-h(x))1-y,用最大似然估计求解参数。 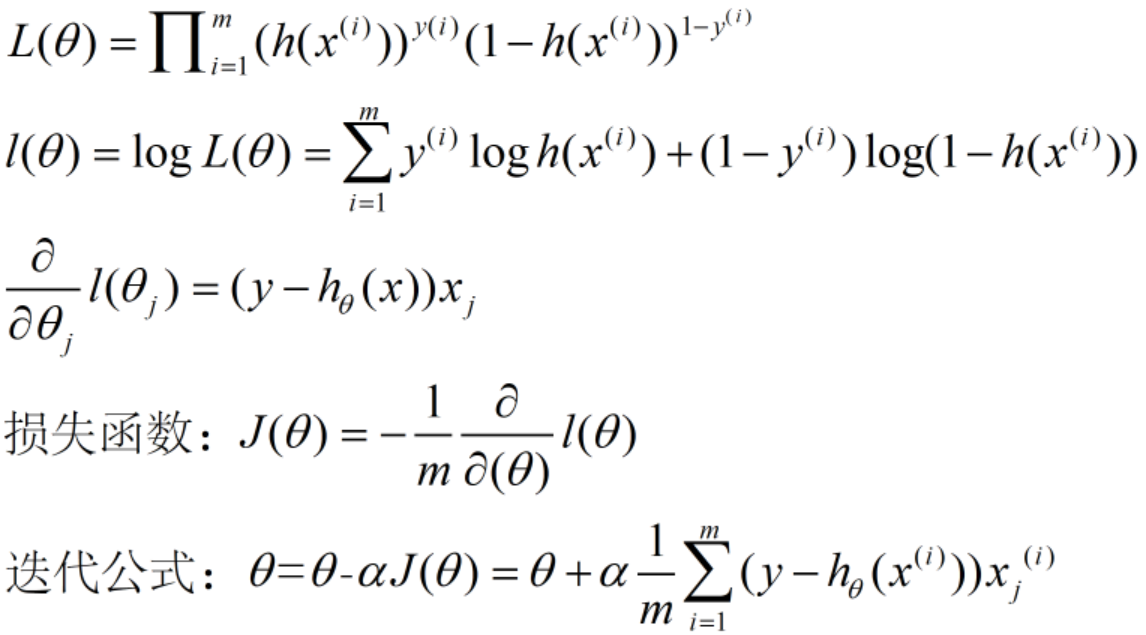
越努力越幸运!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号