NLP问题特征表达基础 - 语言模型（Language Model）发展演化历程讨论

1. NLP问题简介

0x1：NLP问题都包括哪些内涵

人们对真实世界的感知被成为感知世界，而人们用语言表达出自己的感知视为文本数据。那么反过来，NLP，或者更精确地表达为文本挖掘，则是从文本数据出发，来尽可能复原人们的感知世界，从而表达真实世界的过程。这里面就包括如图中所示的模型和算法，包括：

（1）文本层：NLP文本表示； 
（2）文本-感知世界：词汇相关性分析、主题模型、意见情感分析等； 
（3）文本-真实世界：基于文本的预测等；

显而易见，文本表示在文本挖掘中有着绝对核心的地位，是其他所有模型建构的基础。

0x2：为什么要进行文本表示

特征提取的意义在于把复杂的数据，如文本和图像，转化为数字特征，从而在机器学习中使用。

在机器学习项目中，不管是纯NLP问题还是NLP问题和非文本类混合数据的场景，我们都要面临一个问题，如何将样本集中的文本进行特征表征以及通过向量的方式表达出来。

这就要求我们对样本的原始空间进行抽象，将其映射到另一个向量化的特征空间中，笔者在这篇blog中对常用的编码和特征工程方式进行一个梳理总结。

Relevant Link:

https://blog.csdn.net/tiffanyrabbit/article/details/72650606
https://blog.csdn.net/IT_bigstone/article/details/80739807
http://www.cnblogs.com/robert-dlut/p/4371973.html

 

2. 语言模型（Language Model）简介

语言模型本质上是在回答一个问题：出现的语句是否合理（make sense）。

0x1：语言模型发展历史

在历史的发展中，语言模型经历了专家语法规则模型（至80年代），统计语言模型（至00年），神经网络语言模型（till now）。

1. 专家语法规则模型

专家语法规则模型在计算机初始阶段,随着计算机编程语言的发展，归纳出的针对自然语言的语法规则。但是自然语言本身的多样性，口语化，在时间，空间上的演化，及人本身强大的纠错能力，导致语法规则急剧膨胀，不可持续。

2. 统计语言模型

统计语言模型用简单的方式，加上大量的语料，产生了比较好的效果。统计语言模型通过对句子的概率分布进行建模，从统计来来说，概率高的语句比概率底的语句更为合理。

在实现中，通过给定的上文来预测句子的下一个词， 如果预测的词和下一个词是一致（该词在上文的前提下出现的概率比其它词概率要高），那么上文+该词出现的概率就会比上文+其他词词的概率要更大，上文+该词更为合理。

3. 神经网络语言模型

神经网络语言模型在统计语言模型的基础上，通过网络的叠加和特征的逐层提取，可以表征除了词法外，相似性，语法，语义，语用等多方面的表示。

Relevant Link:

https://zhuanlan.zhihu.com/p/28080127

 

3. 统计语言模型(Statistical Language Model, SLM)

统计语言模型是“单个字母/单词/词序列”的概率分布，假设有一个 m 长度的文本序列，统计语言模型的目的是建立一个能够描述给定文本序列对应的概率分布。

0x1：统计语言模型基本公式

统计语言模型从统计（statistic）的角度预测句子的概率分布，通常对数据量有较大要求。

对于句子${\mathrm{w1,w2,...,wn,\; 计算其序列概率为P(w1,w2,...,wn)，根据链式法则可以求得整个句子的概率:}}^{}$ 

 

其中，每个词出现的概率通过统计计算得到： 

即第n个词的出现与前面N-1个词相关，整句的概率就是各个词出现概率的乘积。

0x2：马尔科夫假设：有限前序字符依赖约束条件的统计语言模型

传统的统计语言模型存在几个问题：

1. 参数空间过大，语言模型由于语言的灵活性参数空间维度极高；举个直观的例子，我们有词表 V=10^5 的语料库，学习长度为 l=10 的序列出现概率，潜在参数空间大小为 100000^10=10^50;
2. 数据极度稀疏，长序列的出现频次较低，越长的序列的越不容易出现，整个参数矩阵上会有很多0值;

为了简化问题，我们引入马尔科夫假设：当前词出现的概率仅依赖前$\mathrm{n-1个词，在}$这种假设下，模型就大大减少了需要参与计算的先验参数。

马尔科夫假设的一个具体实现即 n-gram。

当$\mathrm{n=1时，我们称之为unigram(一元语言模型)；}$

$\mathrm{当n=2时，我们称之为bigram(二元语言模型)；}$

$\mathrm{当n=3时，我们称之为trigram(三元语言模型)；}$

$\mathrm{1.\; ngram统计语言模型基本定义}$

n-gram是最为普遍的统计语言模型。它的基本思想是将文本里面的内容进行大小为N的滑动窗口操作，形成长度为N的短语子序列，对所有短语子序列的出现频度进行统计。

举一个具体的例子：

from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    bigram_vectorizer = CountVectorizer(ngram_range=(1, 2), token_pattern=r'\b\w+\b', min_df = 1)
    X_2 = bigram_vectorizer.fit_transform(corpus).toarray()
    print X_2
    print bigram_vectorizer.vocabulary_
'''' 
[[0 0 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0]
 [0 0 1 0 0 1 1 0 0 2 1 1 1 0 1 0 0 0 1 1 0]
 [1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 1 0 0 0]
 [0 0 1 1 1 1 0 1 0 0 0 0 1 1 0 0 0 0 1 0 1]]
{u'and': 0, u'the second': 14, u'is': 5, u'this the': 20, u'one': 8, u'and the': 1, u'second': 9, u'first document': 4, u'is the': 6, u'second document': 10, u'the third': 15, u'document': 2, u'the first': 13, u'is this': 7, u'third': 16, u'this': 18, u'second second': 11, u'third one': 17, u'the': 12, u'this is': 19, u'first': 3}

上面代码中，我们对一段语料进行了bingram处理，并将词汇表打印了出来。

我们看第一行的前3个：0 0 1

索引0的0代表词汇表中索引0对应的bingrame词组[start, and]没有出现在了第一个sentence中；
索引1的0代表词汇表中索引1对应的bingrame词组[and the]没有出现在了第一个sentence中；
索引2的1代表词汇表中索引2对应的bingrame词组[document end]没有出现在了第一个sentence中；
# start、end代表边界占位符

另外，可以看到，ngram编码后得到的向量长度取决于词集的长度。

2. ngram对文本的表征能力

gram并不关注词在样本中的具体位置。n-gram保留的词序列只是它自己的context上下文的词组序列。

因此n-gram编码后的vector丢失了原始sentence sequence的长序列特征，它只保存了N阶子序列的短程依赖关系，无法建立长期依赖。

同时ngram对不同的词组之间的先后信息也丢弃了，原始文本中不同词组出现的先后关系在ngram这里是忽略的。

当n过大时仍会被数据的稀疏性严重影响，实际使用中往往仅使用bigram或trigram。

附：谷歌的统计翻译系统罗塞塔率先使用n-gram=4获得当时市场上最好的性能。

3. n-gram中的平滑(smoothing)

从ngram的公式我们可以看到，随着n的提升，我们拥有了更多的前置信息量，可以更加准确地预测下一个词。但这也带来了一个问题，词组概率分布随着n的提升变得更加稀疏了，导致很多预测概率结果为0。

当遇到零概率问题时，我们可以通过平滑来缓解n-gram的稀疏问题。
n-gram需要平滑的根本原因在于数据的稀疏性，而数据的稀疏性则是由自然语言的本质决定的。当这种稀疏性存在的时候，平滑总能用于缓解问题提升性能。 直观上讲，如果你认为你拥有足够多的数据以至于稀疏性不再是一个问题，我们总是可以使用更加复杂、更多参数的模型来提升效果，如提高n的大小。当n提高，模型参数空间的指数级增加，稀疏性再度成为了所面临的问题，这时通过合理的平滑手段可以获得更优的性能。

参考Andrew Gelman的一句名言：样本从来都不是足够大的。如果 N 太大不足以进行足够精确的估计，你需要获得更多的数据。但当 N “足够大”，你可以开始通过划分数据研究更多的问题，例如在民意调查中，当你已经对全国的民意有了较好的估计，你可以开始分性别、地域、年龄进行更多的统计。N 从来都无法做到足够大，因为当它一旦大了，你总是可以开始研究下一个问题从而需要更多的数据。

1）什么时候需要概率平滑处理

在一个有限的数据集中，高频事件通过统计所求得的概率更加可靠，而出现频次越小的事件所得的概率越不可靠，这种现象在高维空间中表现更加突出。

如果将训练集的概率分布直接拿来作为测试集分布，那么训练集中的“未登录词”概率将会是0，这显然与我们的先验认知是不符合的，因为测试集中是有可能出现未登录词的，没见过的不代表不存在。

平滑解决的问题就是：根据训练集数据的频率分布，估计在测试集中“未登录词”的概率分布，从而在测试集上获得一个更加理想的概率分布预估 。也可以理解为在原始的样本驱动的概率分布之上附加了一个先验正则化，通过先验分布来干预侯后验概率分布。

接下来我们对常用的平滑方法进行介绍。

2）拉普拉斯平滑(Laplace Smoothing)

如公式所示，拉普拉斯平滑对所有事件的频次均进行了加1。

拉普拉斯平滑是最为直观、容易理解的平滑方式，对事件发生的频次加一对于高频事件的概率影响基本可以忽略，它也同时解决了未登录词的概率计算问题。
但直接加1的拉普拉斯平滑也是一种较为“糟糕”的平滑方式，简单粗暴的加1有时会对数据分布产生较大的影响，有时却又微不足道。拉普拉斯平滑对未知事件的概率预测进行了平等对待，这显然不合理！

3）加性平滑(Additive Smoothing)

在加性平滑中我们做出以下假设：我们假定每个n-gram事件额外发生过 $\mathrm{\delta 次；}$

$\mathrm{一般而言0<\delta <=1,\; 当\delta =1时等价于拉普拉斯平滑；当\delta <1\delta <1时，表示对未登录词的概率分配权重减少。}$

$\mathrm{这种方法提升了拉普拉斯平滑的泛用性。}$

4）古德图灵平滑(Good Turing Smoothing)

古德图灵平滑是一种非常”动态柔软“的平滑方式，笔者自己非常喜欢这类数学公式，他并不是生硬地增加或者减少某个具体的实数值，而是根据当前上下文动态决定调整的程度。

假定某个事件实际出现 r 次，调整后频次为 ${\mathrm{r\ast \; 次，nr 表示n-gram中恰好出现\; r\; 次的不同序列数，nr+1类似。}}^{}$

${\mathrm{这个公式的合理性在哪里呢？}}^{}$

直观上讲，它通过高频事件优化低频事件的概率表示，并最终通过层层迭代获取到未登录词的概率。根据Zipf's law，${\mathrm{nr分布如下图所示(横轴为r，纵轴为nr)，由图可知，通常而言 r\ast <r}}^{}$

一般来说，出现一次的词的数量比出现两次的多，出现两次的比三次的多，高频词到低频次的出现频次下降趋势大致呈现上图所示规律，这种规律称为Zipf定律（Zipf’s Law）。

4. 基于n-gram的机器学习应用

1）基于ngram定义的两个字符串的距离

模糊匹配的关键在于如何衡量两个长得很像的单词(或字符串)之间的“差异”，这种差异通常又称为“距离”。除了可以定义两个字符串之间的编辑距离(通常利用Needleman-Wunsch算法或Smith-Waterman算法)，还可以定义它们之间的Ngram距离。

假设有一个字符串S，那么该字符串的Ngram就表示按长度N切分原sentence得到的词段(长度为N)，也就是S中所有长度为N的子字符串。设想如果有两个字符串，然后分别求它们的Ngram，那么就可以从它们的共有子串的数量这个角度去定义两个字符串间的Ngram距离。但是仅仅是简单地对共有子串进行计数显然也存在不足，这种方案显然忽略了两个字符串长度差异可能导致的问题。比如字符串girl和girlfriend，二者所拥有的公共子串数量显然与girl和其自身所拥有的公共子串数量相等，但是我们并不能据此认为girl和girlfriend是两个等同的匹配。为了解决该问题，有研究员提出以非重复的Ngram分词为基础来定义Ngram距离，公式表示如下：

|GN(S1)|+|GN(S2)|−2×|GN(S1)∩GN(S2)|

此处，|GN(S1)||GN(S1)|是字符串S1S1的Ngram集合，N值一般取2或者3。以N=2为例对字符串Gorbachev和Gorbechyov进行分段，可得如下结果

Go or rb ba ac ch he ev
Go or rb be ec ch hy yo ov

结合上面的公式，即可算得两个字符串之间的距离是8 + 9 − 2 × 4 = 9。显然，字符串之间的距离越小，它们就越接近。当两个字符串完全相等的时候，它们之间的距离就是0。可以看到，这种公式充分考虑到了字符串的长度区别和相同词组2者的共同作用

2）利用ngram模型评估语句是否合理

从统计的角度来看，自然语言中的一个句子S可以由任何词串构成，不过概率P(S)有大有小。例如：

S1 = 我刚吃过晚饭
S2 = 刚我过晚饭吃

显然，对于中文而言S1是一个通顺而有意义的句子，而S2则不是，所以对于中文来说P(S1)>P(S2)

假设我们现在有一个语料库如下，其中<s1><s2>是句首标记，</s2></s1>是句尾标记：

<s1><s2>yes no no no no yes</s2></s1>
<s1><s2>no no no yes yes yes no</s2></s1>

下面我们的任务是来评估如下这个句子的概率：

<s1><s2>yes no no yes</s2></s1>

我们利用trigram来对这句话进行词组分解

所以我们要求的概率就等于：1/2×1×1/2×2/5×1/2×1=0.05

3）在实际项目中需要注意的问题

词袋模型编码得到的词向量长度，等于词袋中词集的个数。

然而，通常在一个海量的document集合中，词集的个数是非常巨大的。如果全部都作为词集，那么最终编码得到的词向量会非常巨大，同时也很容易遇到稀疏问题。

因此，我们一般需要在特征编码前进行padding or truncating，具体的做法可以由以下两种：

1. 根据TOP Order排序获取指定数量的词集，例如取 top 8000高频词作为词集；
2. 针对编码后得到的词向量进行 padding or truncating

这两种做法的最终效果是一样的。

Relevant Link:

http://blog.csdn.net/lengyuhong/article/details/6022053
https://flystarhe.github.io/2016/08/16/ngram/
http://blog.csdn.net/baimafujinji/article/details/51281816
https://en.wikipedia.org/wiki/Bag-of-words_model
http://www.52nlp.cn/tag/n-gram
https://blog.csdn.net/tiffanyrabbit/article/details/72650606

0x3：独立同分布假设：所有字符间都独立同分布的的统计语言模型

独立同分布假设是对马尔科夫假设的进一步，即假设所有字符之间连前序关系都不存在，而是一个个独立的字符，这和朴素贝叶斯的独立同分布假设本质上在思想上是一致的，都是通过增加先验约束，从而显著减小参数搜索空间。

1. 词袋bow统计语言模型基本定义

词袋模型，顾名思义，把各种词放在一个文本的袋子里，即把文本看做是无序的词的组合。利用统计语言模型来理解词序列的概率分布。

文本中每个词出现的概率仅与自身有关而无关于上下文。这是对原始语言模型公式的最极端的简化，丢失了原始文本序列的前序依赖信息。

对于一个文档（document），忽略其词序、语法、句法，将其仅仅看做是一个词集合，或者说是词的一个组合，文档中每个词的出现都是独立的，不依赖于其他词是否出，即假设这篇文章的作者在任意一个位置选择一个词汇都不受前面句子的影响而独立选择的。这是一种非常强的假设，比马尔科夫假设还要强。

2. 词库表示法合理性依据

词库模型依据是：存在类似单词集合的文章的语义同样也是类似的

3. 词库编码代码示例

from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    vectorizer = CountVectorizer(min_df=1)
    X = vectorizer.fit_transform(corpus)
    print vectorizer.get_feature_names()
    print X.toarray()

''''
[u'and', u'document', u'first', u'is', u'one', u'second', u'the', u'third', u'this']
总体样本库中共有9个token word

[[0 1 1 1 0 0 1 0 1]
 [0 1 0 1 0 2 1 0 1]
 [1 0 0 0 1 0 1 1 0]
 [0 1 1 1 0 0 1 0 1]]
每一行代表一个sentence，共4行(4个sentence)
每一列代表一个token词的词频，共9列(9个token word)
''''

对运行的结果我们仔细观察下，第一个sentence和最后一个文本sentence分别表达了陈述和疑问两种句式(token word出现的位置不一样，造成表达意思的不同)，但是因为它们包含的词都相同。所以经过词袋编码后，得到的特征向量都是一样的。

很显然，这个编码过程丢失了这个疑问句的句式信息，这就是词袋模型最大的缺点：不能捕获词间相对位置信息。

'This is the first document.',
'Is this the first document?',

[[0 1 1 1 0 0 1 0 1] 
 [0 1 1 1 0 0 1 0 1]]

Relevant Link:

http://www.cnblogs.com/platero/archive/2012/12/03/2800251.html
http://feisky.xyz/machine-learning/resources/github/spark-ml-source-analysis/%E7%89%B9%E5%BE%81%E6%8A%BD%E5%8F%96%E5%92%8C%E8%BD%AC%E6%8D%A2/CountVectorizer.html

0x4：局部与整体分布假设：TF-IDF（Term Frequency-Inverse Document Frequency）表示法

TF-IDF(term frequency–inverse document frequency)是一种用于信息检索与数据挖掘的常用加权技术。

TF-IDF产生的特征向量是带有倾向性的，主要可以被用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。

字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。

TF-IDF属于BOW语言模型的一种，但是在基础的词频统计之上增加和单个词和全局词集的相对关系。同时，TF-IDF也不关注词序信息，TF-IDF同样也丢失了词序列信息。

1. TF-IDF的加权词频统计思想

用通俗的话总结TF-IDF的主要思想是：

如果某个词或短语在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类，也即可以作为所谓的关键字。

假定现在有一篇长文《中国的蜜蜂养殖》，我们准备用计算机提取它的关键词，一个容易想到的思路，就是找到出现次数最多的词。如果某个词很重要，它应该在这篇文章中多次出现。

于是，我们进行"词频"（Term Frequency，缩写为TF）统计。

在统计结束后我们会发现，出现次数最多的词是 "的"、"是"、"在" 这一类最常用的词。它们叫做"停用词"(stop words)，在大多数情况下这对找到结果毫无帮助、我们采取过滤掉停用词的策略。

假设我们把它们都过滤掉了，只考虑剩下的有实际意义的词。这样又会遇到了另一个问题，我们可能发现"中国"、"蜜蜂"、"养殖"这三个词的出现次数一样多。这是不是意味着，作为关键词，它们的重要性是一样的？

显然不是这样。因为"中国"是很常见的词(在日常的语料库中出现频率较高)，相对而言，"蜜蜂"和"养殖"不那么常见(倾向于专有领域的词)。

如果这三个词在一篇文章的出现次数一样多，有理由认为，"蜜蜂"和"养殖"的重要程度要大于"中国"，也就是说，在关键词排序上面，"蜜蜂"和"养殖"应该排在"中国"的前面。所以，我们需要一个重要性调整系数，衡量一个词是不是常见词。如果某个词比较少见，但是它在这篇文章中多次出现，那么它很可能就反映了这篇文章的特性，正是我们所需要的关键词

用统计学语言表达，就是在词频的基础上，要对每个词分配一个"重要性"权重

1. 最常见的词("的"、"是"、"在")给予最小的权重；
2. 较常见的词("中国")给予较小的权重；
3. 较少见的词("蜜蜂"、"养殖")给予较大的权重；

这个权重叫做"逆文档频率"（Inverse Document Frequency，缩写为IDF），它的大小与一个词的常见程度成反比，它的作用是对原始词频权重进行反向调整。

知道了"词频"（TF）和"逆文档频率"（IDF）以后，将这两个值相乘，就得到了一个词的TF-IDF值。某个词对文章的重要性越高，它的TF-IDF值就越大。所以，排在最前面的几个词，就是这篇文章的关键词

2. TF-IDF算法流程

第一步 - 计算词频

考虑到文章有长短之分，为了便于不同文章的比较，进行"词频"归一化"

第二步 - 计算逆文档频率

这时，需要一个语料库（corpus），用来模拟语言的总体使用环境

如果一个词越常见，那么分母就越大，逆文档频率就越小越接近0。分母之所以要加1，是为了避免分母为0（即所有文档都不包含该词），log表示对得到的值取对数。

第三步 - 计算TF-IDF

可以看到，TF-IDF与一个词在文档中的出现次数成正比，与该词在整个语言中的出现次数成反比

以《中国的蜜蜂养殖》为例：

假定该文长度为1000个词，"中国"、"蜜蜂"、"养殖"各出现20次，则这三个词的"词频"（TF）都为0.02。然后，搜索Google发现，包含"的"字的网页共有250亿张，假定这就是中文网页总数包含"中国"的网页共有62.3亿张；包含"蜜蜂"的网页为0.484亿张；包含"养殖"的网页为0.973亿张。

则它们的逆文档频率（IDF）和TF-IDF如下

中国
IDF = math.log(250 / 63.3) = 1.37357558871
TF-IDF = IDF * 0.02 = 0.0274715117742

蜜蜂
IDF = math.log(250 / 63.3) = 5.12671977312 
TF-IDF = IDF * 0.02 = 0.102534395462

养殖
IDF = math.log(250 / 63.3) = 4.84190569082 
TF-IDF = IDF * 0.02 = 0.0968381138164

从上表可见，"蜜蜂"的TF-IDF值最高，"养殖"其次，"中国"最低。所以，如果只选择一个词，"蜜蜂"就是这篇文章的关键词

3. TF-IDF的sklearn封装实现

因为 tf–idf 在特征提取中经常被使用，所以有一个类: TfidfVectorizer 在单个类中结合了所有类和类中的选择:

from sklearn.feature_extraction.text import TfidfVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    vectorizer = TfidfVectorizer(min_df=1)
    tfidf = vectorizer.fit_transform(corpus)
    print vectorizer.vocabulary_
    print tfidf.toarray()
''''

{u'and': 0, u'third': 7, u'this': 8, u'is': 3, u'one': 4, u'second': 5, u'the': 6, u'document': 1, u'first': 2}
[[ 0.          0.43877674  0.54197657  0.43877674  0.          0.        0.35872874  0.          0.43877674]
 [ 0.          0.27230147  0.          0.27230147  0.          0.85322574    0.22262429  0.          0.27230147]
 [ 0.55280532  0.          0.          0.          0.55280532  0.        0.28847675  0.55280532  0.        ]
 [ 0.          0.43877674  0.54197657  0.43877674  0.          0.        0.35872874  0.          0.43877674]]

可以看到，document在整个语料库中都出现，所以权重被动态降低了

Relevant Link:

http://www.ruanyifeng.com/blog/2013/03/tf-idf.html
http://www.cnblogs.com/ybjourney/p/4793370.html
http://www.cc.ntu.edu.tw/chinese/epaper/0031/20141220_3103.html
https://nlp.stanford.edu/IR-book/html/htmledition/tf-idf-weighting-1.html
http://sklearn.lzjqsdd.com/modules/feature_extraction.htm

 

4. LSA - 一种基于SVD矩阵奇异值分解的语义分析语言模型

0x1：文本分类中常出现的问题 - 歧义与多义

1. 一词多义

比如 bank 这个单词如果和 mortgage，loans，rates 这些单词同时出现时，bank 很可能表示金融机构的意思；

可是如果 bank 这个单词和 lures，casting，fish一起出现，那么很可能表示河岸的意思；

2. 一义多词

比如用户搜索“automobile”，即汽车，从词义层面上讲，用户可能对包含“car”单词的页面也感兴趣。 

0x2：LSA（Latent Semantic Analysis）基本介绍

潜在语义分析LSA（Latent Semantic Analysis ）也叫作潜在语义索引LSI（ Latent Semantic Indexing ） 顾名思义是通过分析文章（documents ）来挖掘文章的潜在意思或语义（concepts ）。

不同的单词可以表示同一个语义，或一个单词同时具有多个不同的意思，这些的模糊歧义是LSA主要解决的问题。

例如上面所说，bank 这个单词如果和 mortgage, loans, rates 这些单词同时出现时，bank 很可能表示金融机构的意思。可是如果bank 这个单词和lures, casting, fish一起出现，那么很可能表示河岸的意思。

1. 最小语义子集

一篇文章（包含很多sentence的document）可以随意地选择各种单词来表达，因此不同的作者的词语选择风格都大不相同，表达的语义也因此变得模糊。

这种单词选择的随机性必然将噪声的引入到“单词-语义关系”（word-concept relationship）。

简单来说，LSA做的事是降维，通过对语料库中的海量单词进行降维，在语料库中找出一个最小的语义子集（ smallest set of concepts），这个最小语义子集就是新的词向量集合。

0x3：LSA背后涉及到的线性代数理论

这部分内容笔者正在整理丘维声教授的线性代数相关章节知识，会在详细梳理后补充迭代到这个章节里面。

https://blog.csdn.net/zkl99999/article/details/43523469

1）词-文档矩阵（Occurences Matrix) - 将原始document转换为词频统计稀疏矩阵

LSA 使用词-文档矩阵来描述一个词语是否在一篇文档中。

词-文档矩阵式一个稀疏矩阵，其行代表词语，其列代表文档。

一般情况下，词-文档矩阵的元素是该词在文档中的出现次数（词库表示法），也可以是是该词语的TF-IDF。词-文档矩阵的本质就是传统的词频语言模型，后面的LSA语义分析在基于传统的词频语言模型进行了拓展。

2）SVD奇异值矩阵分解 - 降维

在构建好词-文档矩阵之后，LSA将对该矩阵进行降维，来找到词-文档矩阵的一个低阶近似。降维的原因有以下几点：

1. 原始的词-文档矩阵太大导致计算机无法处理，从此角度来看，降维后的新矩阵式原有矩阵的一个近似；
2. 原始的词-文档矩阵中有噪音，从此角度来看，降维后的新矩阵式原矩阵的一个去噪矩阵，即冗余信息压缩；
3. 原始的词-文档矩阵过于稀疏。原始的词-文档矩阵精确的反映了每个词是否“出现”或“出现的频次”于某篇文档的情况，然而我们往往对某篇文档“相关”的所有词更感兴趣，因此我们需要发掘一个词的各种同义词的情况；
4. 将维可以解决一部分同义词的问题，也能解决一部分二义性问题。具体来说，原始词-文档矩阵经过降维处理后，原有词向量对应的二义部分会加到和其语义相似的词上，而剩余部分则减少对应的二义分量；

降维的结果是不同的词或因为其语义的相关性导致合并，如下面将car和truck进行了合并：

{(car), (truck), (flower)} --> {(1.3452 * car + 0.2828 * truck), (flower)} 

3）SVD降维推导

假设 X 矩阵是词-文档矩阵，其元素（i，j）代表词语 i 在文档 j 中的出现次数，则 X矩阵看上去是如下的样子：

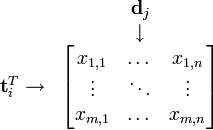
可以看到，每一行代表一个词的向量，该向量描述了该词和所有文档的关系。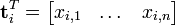

相似的，一列代表一个文档向量，该向量描述了该文档与所有词的关系。

词向量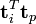的点乘可以表示这两个单词在文档集合中的相似性。矩阵 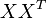包含所有词向量点乘的结果，元素（i，p）和元素（p，i）具有相同的值，代表词 p 和词 i 的相似度。

类似的，矩阵包含所有文档向量点乘的结果，也就包含了所有文档总体的相似度。

现在假设存在矩阵的一个分解，即矩阵可分解成正交矩阵U和V，和对角矩阵的乘积。

这种分解叫做奇异值分解（SVD），即：

因此，词与文本的相关性矩阵可以表示为：

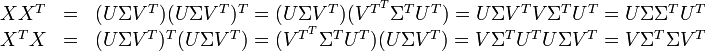
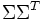因为与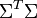是对角矩阵，因此 肯定是由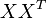的特征向量组成的矩阵，同理是特征向量组成的矩阵。这些特征向量对应的特征值即为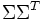中的元素。综上所述，这个分解看起来是如下的样子：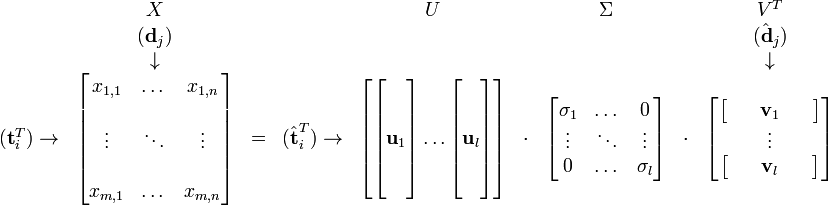

 

 被称作是奇异值，而  和则叫做左奇异向量和右奇异向量。

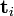通过矩阵分解可以看出，原始矩阵中的 只与U矩阵的第 i 行有关，我们则称第 i 行为 。

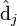同理，原始矩阵中的只与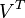中的第 j 列有关，我们称这一列为。

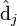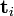与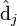并非特征值，但是其由矩阵所有的特征值所决定。

当我们选择 k 个最大的奇异值，和它们对应的Ｕ与Ｖ中的向量相乘，则能得到一个X矩阵的 k 阶近似，此时该矩阵和X矩阵相比有着最小误差（即残差矩阵的Frobenius范数）。

但更有意义的是这么做可以将词向量和文档向量映射到语义空间。

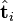向量与含有 k 个奇异值的矩阵相乘，实质是从高维空间到低维空间的一个变换，可以理解为是一个高维空间到低维空间的近似。

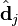同理，向量 也存在这样一个从高维空间到低维空间的变化。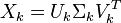

这种变换用公式总结出来就是这个样子：

Relevant Link: 

https://blog.csdn.net/roger__wong/article/details/41175967
https://blog.csdn.net/zhzhji440/article/details/47193731

 

5. 神经网络语言模型（neural network language model, NNLM）(2003年)

0x1：传统统计语言模型的问题

统计语言模型在学习单词序列的联合概率时，一个比较显然的问题是维度灾难，计算和存储参数巨多，在高维下，数据稀疏会导致统计语言模型存在很多为零的条件概率。

至于为什么会存在高维空间中，词向量会出现概率稀疏问题，笔者有自己的一个理解，我们可以从Johnson–Lindenstrauss定理中得到启发。简单说来，它的结论是这样的：一个一百万维空间里的随便一万个点，一定可以几乎被装进一个几十维的子空间里！

举一个形象的例子说明，即高维物体之间的“间隙”可能很大，换句话说高维空间是非常“空旷”、”稀疏“的。

从简单的2维开始举例：下图单位正方形内部有四个直径为0.5的圆把它充满，那么这些圆之间的空隙中能填上的最大小圆（红色那个）的直径约为0.21。

如果换成三维单位正方体，则情况如下图。此时红色小球的直径约为0.37，比2维时变大了。

再往高维走，这个间隙中的小球直径可以用如下方法计算： ，其中n为维度数。

我们会发现：这个“填缝隙的小球”的直径居然可以无限增大！事实上在4维的时候，小球的直径达到0.5，这就和周围那些球一样大了。而到了9维的时候，小球已经膨胀到能接触正方体的壁了。

形象点说：高维沙堆之间的空隙能轻易放下一堆高维大西瓜。

那这些和统计语言模型的高维稀疏问题有什么关系呢？

简单来说，由于自然语言本身的特性，词集空间越大，维度就越高，就越容易出现高维稀疏问题，一段自然语言句子常常会分布在高维空间的高维部分，而低维部分大量浪费了。

后面要介绍的词向量主要就是解决该问题，将每个词”相对均匀“地分布到一个维度相对适中的词向量空间中，避免了维度稀疏。

词向量的核心思想是，不从词频角度来对文本进行建模，而是将所有词都看作是一个向量空间中的一个向量，这就不存在”未登录词“的问题，所有的词都被映射到向量空间中某个向量点。

Relevant Link: 

https://blogs.scientificamerican.com/roots-of-unity/why-you-should-care-about-high-dimensional-sphere-packing/   
https://zh.wikipedia.org/zh-hant/%E7%BA%A6%E7%BF%B0%E9%80%8A-%E6%9E%97%E7%99%BB%E6%96%AF%E7%89%B9%E5%8A%B3%E6%96%AF%E5%AE%9A%E7%90%86
https://www.zhihu.com/question/32210107
http://imaginary.farmostwood.net/573.html 

0x2：分布式表征（distributed representation）词向量概念

1. word embedding词向量历史

NNLM 最早由Bengio系统化提出并进行了深入研究[Bengio, 2000, 2003]。当然分开来看，(1) distributed representation最早由Hinton提出(1985), (2)利用神经网络建模语言模型由Miikkulainen and Dyer，Xu and Rudnicky分别在1991和2000提出。

Bengio提出词向量的概念，代替ngram使用离散变量(高维)，采用连续变量(具有一定维度的实数向量)来进行单词的分布式表示，解决了维度爆炸的问题，同时通过词向量可获取词之间的相似性。

2. 什么是分布式表征词向量？和传统的词频统计词向量有什么区别？

传统的词频统计模型是one-hot类型的，每个词都是一个 |V| 长度的且只有一位为1，其他位都为0的定长向量。每个词向量之间都是完全正交的，相关性为0。虽然可以实现对原始语料进行编码的目的，但是对不同的词之间的相似性、语法语义的表征能力都很弱。

为了解决这个问题，Hinton教授提出了分布式表征词向量，先来直观地看一下什么是分布式表征词向量，下面是一组将高维词向量通过t-SNE降维到2维平面上进行可视化展示的截图。

可以看到，在该二维图中，每一个词不仅对应了一个向量（词向量化编码）。同时相似的词之间，例如“are”和“is”是紧挨在一起的。

通过这个图，我们可以很直观地对这个所谓的分布式表征词向量的特性作一个猜想：

1. 首先，这个所谓的分布式表征词向量依然是一个定长的向量，每个词向量都位于同一个向量空间中；
2. 词向量之间具有明显的空间相关性（这里借用了线性先关的概念思想），即相似的词都明显聚集在某一个空间区域中，用其中一个词可以表达(代替)这个区域中的所有词。相对的，不相似的词分布在空间中的不同区域；

这么美妙的特性是怎么得到的呢？接下来我们来深入讨论。

笔者思考：在学习word embedding之前，读者朋友可以先进行一个前导思考，思考一下AutoEncoder的核心原理，或者更本质的，我们思考一下神经网络的全连接隐层到底代表着什么？

从线性代数角度来看，神经网络的隐藏层接受输入层向量，经过权重系数矩阵对应的线性变换(linear transformation)之后，原始的输入向量被变换到了另一个向量空间中。通过末端损失函数的BP负反馈，反过来不断调整隐层系数矩阵对应的向量空间的概率分布，最终当损失函数收敛时，隐藏层的系数矩阵对应的向量空间的概率分布是“最有利于”预测值靠近目标函数的。这点其实并不难理解，只是我们在学习神经网络初期可能更关注的是神经网络末端的输出层，毕竟输出层才是我们要的二分类/多分类/概率预测的有用结果，而对训练结束后，隐藏层到底长什么样并不十分关心。

可以看到，隐藏层会朝什么方向调整，取决于神经网络末端的损失函数。如果我们的用一个表达语法语义结构的概率似然函数来作为损失函数进行BP优化，则可以想象，训练收敛后，隐藏层的概率分布会趋向于和语料集中的语法语义结构同构。

对类似的原理感兴趣的读者朋友可以google一些作CNN隐藏层可视化的文章和代码，通过将CNN的隐藏层进行反向激活后可视化，可以看到CNN的每一个隐藏层都代表了一种特定的细节滤波器，都具有明显的几何纹理特征。

3. 用似然函数来表征语言模型的条件概率 - 语法语义结构表征

需要强调的是，本文介绍的所有语言模型都是在基本语言模型（language model）框架之下的，区别仅仅在于用于表达每个词向量的生成过程和表达方式不同。

语言模型本质上是一个概率分布模型  ，对于语言里的每一个字符串  给出一个概率  。假设有一个符号的集合  ，我们不妨把每一个  称作一个“单词”，由零个或多个单词连接起来就组成了一个字符串  ，字符串可长可短，例如实际语言中的句子、段落或者文档都可以看作一个字符串。

所有合法（例如，通过一些语法约束）的字符串的集合称作一个语言，而一个语言模型就是这个语言里的字符串的概率分布模型。

可实际上越远的词语其实对该词的影响越小，那么如果考虑一个n-gram, 每个词都只受其前面n-1个词的影响，所以我们加入了马尔科夫假设之后，则有：

上面公式定义非常清晰，但是不是非常直观，我们举一个例子：

假设我们的语料只有一句话：我爱祖国

如果用传统语言模型，对应的联合概率分布就是：P（我，爱，祖，国） = P（我 | start）+ P（爱 | 我）+ P（祖 | 爱，我）+ P（国 | 祖，爱，我）

加入马尔科夫假设后，即只考虑一个ngram范围内的前序词，对应的联合概率分布就是（以2-gram为例）：P（我，爱，祖，国） = P（我 | start）+ P（爱 | 我）+ P（祖 | 爱）+ P（国 | 祖）

上述就是基本的语言模型（language model）。

接下来的问题，这个条件概率如何计算呢？

如果是统计语言模型，条件概率是通过统计对应的ngram词序列的出现次数来计算的，也就是词频，具体方法可以回到之前章节的讨论。

备注：我们熟悉的朴素贝叶斯判别器就是一个词频统计语言模型的应用

但我们知道，词频统计很容易遇到“未登录词”的问题，虽然有很多平滑手段，但是无法100%解决该问题。

神经网络不再使用词频来作为统计工具，而是直接基于似然函数（例如tahn、sigmoid）来计算条件概率。

同时，这个模型需要满足的概率累加和约束，即对于任意的，表示与上下文所有可能的组合的概率和为1。 

这看起来太美好了，我们可以有一个函数可以直接得到语句对应的【0，1】值域内的概率值！不用再保存大量的ngram词频统计结果。那接下来的问题就是，似然函数形式如何？似然函数值如何计算呢？显然不像词频统计那样直接进行一个 count/N 就可以的。

4. Bengio NIPS’03 Model - N-gram neural model

Bengio使用前馈神经网络（FFNN，Feed Forward Neural Network）表示f，其结构如下：

1）输入层

这里所谓的ngram neural，通俗的解释是说神经网络的输入层是ngram的形式。如上面流程图所示，最下方绿色方块代表了一组ngram词序列。这么做的原因和ngram统计语言模型是一样的，为了捕获词序列的短程依赖特征。

输入层的size由ngram序列长度决定。

2）全连接隐层 - 词向量矩阵层

接下来，我们需要定义词向量嵌入空间（embedding空间）的维度，读者朋友在TensorFlow编程中对这个参数应该非常熟悉了，就是output_dim参数，在NLP项目开发中，我们一般会设置64/128/256这样的值，这里记作 m。

这层隐层实际上构建了一个的矩阵C（m 行 |V| 列），每个词都对应一个m维的列向量，总共 |V| 个单词。这个矩阵C作为一个shared super parameters在整个隐层所有神经元中共享。

这个系数矩阵C非常重要，它既是训练过程中将每次词转换为一个m维向量的lookup-table，也是最终训练完成后，我们得到的”词嵌入向量表“。

通过训练的负反馈调整，矩阵C中初始的每一个m维向量都进行了调整，使得和训练预料和语法和语义最匹配。

映射矩阵将输入的每个单词$\mathrm{映射到实数向量}$

如前所述，每次向神经网络输入一个ngram词序列，句子单词${\mathrm{以onehot形式作为输入，与共享矩阵C做矩阵相乘得到索引位置的词向量（其实就是一个查表过程）。}}^{}$

拼接得到一个新的向量 e

3）非线性变换层

经过非线性层

4）softmax输出层 - 条件概率输出层

输出层为Softmax，保证满足概率分布累加和为1的约束，生成每一个（总共 |V| 个）目标词wt的概率为：

softmax输出的是一个长度为 |V|、且累加和为1的的向量，例如[0.01, ..., 0.05]

5）损失函数

在神经网络的损失计算中，我们需要计算按照神经网络的正向传播计算的分数S1，和按照正确标注计算的分数S2（目标值），之间的差距，计算Loss，才能应用反向传播。

整个网络的损失值(cost)为多类分类交叉熵（类型数为 |V|），用公式表示为

其中表示第 i 个样本第 k 类的真实标签(0或1)，表示第 i 个样本第 k 类softmax输出的概率。

6）反向传播负反馈

模型的训练目标是最大化以下似然函数：

其中 θ 为模型的所有参数，R(θ) 为正则化项。

模型求解方式采用随机梯度上升（SGA，Stochastic Gradient Ascent），SGA类似于SGD，仅目标函数存在min和max的区别。

5. 词嵌入向量是神经网络训练的副产品

我们可以将这个网络理解为在传统ngram之上的一种stacking升级，在ngram之上加上了神经网络。通过神经网络，在大语料集上通过神经网络的梯度向上进行训练，即联合概率最大似然目标函数，当完成训练后，神经网络的副产品，也就是输入层的对应的”词汇表中每个词对应的分布式向量表示“就是我们要的词向量。

Relevant Link: 

https://www.zhihu.com/question/62060876
http://blog.pluskid.org/?p=352 
http://www.jmlr.org/papers/volume3/bengio03a/bengio03a.pdf
https://www.zhihu.com/question/23765351
http://www.paddlepaddle.org/documentation/docs/zh/0.14.0/new_docs/beginners_guide/basics/word2vec/index.html
https://blog.csdn.net/u010089444/article/details/52624964
http://www.flickering.cn/nlp/2015/03/%E6%88%91%E4%BB%AC%E6%98%AF%E8%BF%99%E6%A0%B7%E7%90%86%E8%A7%A3%E8%AF%AD%E8%A8%80%E7%9A%84-3%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E8%AF%AD%E8%A8%80%E6%A8%A1%E5%9E%8B/

0x3：embedding词向量的一个示例 

# -*- coding: utf-8 -*-

texts = [
    'This is a text',
    'This is not a text',
    'This is an text'
]

from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences 
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Embedding

max_review_length = 6         # maximum length of the sentence
embedding_vecor_length = 3    # embedding dimension
top_words = 10

# num_words is tne number of unique words in the sequence, if there's more top count words are taken
tokenizer = Tokenizer(top_words)
tokenizer.fit_on_texts(texts)
sequences = tokenizer.texts_to_sequences(texts)
word_index = tokenizer.word_index
print('Found %s unique tokens.' % len(word_index))
print "word_index: ", word_index

#max_review_length is the maximum length of the input text so that we can create vector [... 0,0,1,3,50] where 1,3,50 are individual words
data = pad_sequences(sequences, max_review_length)

# 原始语料经过embedding编码得到的词向量联合结果
print('shape of data tensor:', data.shape)
print(data)

 
model = Sequential()
model.add(Embedding(top_words, embedding_vecor_length, input_length=max_review_length,mask_zero=True))
model.compile(optimizer='adam', loss='categorical_crossentropy')
output_array = model.predict(data)
print "output_array: ", output_array

# 打印出embedding层每一个神经元（即每一个词）对应的词嵌入向量（这里是3维）
print "model.layers[0].get_weights(): ", model.layers[0].get_weights()

Relevant Link:  

https://keras.io/layers/about-keras-layers/
https://stackoverflow.com/questions/45649520/explain-with-example-how-embedding-layers-in-keras-works
https://keras.io/zh/layers/embeddings/ 

0x4：为什么NNLM经过训练后，词向量之间会形成相似相聚，相异相远的情况

我们现在已经对NNLM的词向量特性很理解了，词向量真是太美妙了，它有很多非常棒的特性，非常适合在NLP任务中作为input layer使用。

这个章节我们来继续深入讨论下，词向量能够在向量空间上表达出和语法/语义近似吻合的空间聚集和空间疏远结构，其背后的原理是啥。

1. 向量的cosine夹角余弦相似度 - 词向量相似性度量的理论基础

余弦夹角是几何数学中的概念，用来度量两个向量之间的夹角。余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。 

反之，如果a和b向量夹角较大，或者反方向，则说明这两个向量有较低的相似性。

2. NNLM网络的训练过程本质就是一个夹角余弦函数的回归训练过程

我们换一个抽象视角来看NNLM网络，将其整个隐层看做是一个夹角余弦函数。

将输入文本的马尔科夫概率累乘公式：

改成成输入文本的词向量之间的cosine夹角余弦的累乘公式：

训练中，BP过程从output层的softmax开始链式求导（或者直接计算Hessian矩阵），逐层调整其权重w， 对于词向量所在的隐层来说，本质上调整的是其空间分布，最终，相似的词之间的词向量的cosine夹角会变小，相异的词的词向量的cosine夹角会变大，最终收到到某个空间结构上。

3. 通过一个从二元线性回归的训练过程来理解词向量的训练过程

我们假设一个2维的词向量，将其目标值（label）和训练收敛后的词向量（2-dim word vector）显示在二维平面上，如下：

上图中，语料库中的sentence是不同单词的次词向量的累乘结果（cosine夹角余弦），通过训练，不同的组成相同sentence的词向量的权重w收敛到空间上相近的区域。

Relevant Link:   

https://baike.baidu.com/item/%E4%BD%99%E5%BC%A6%E7%9B%B8%E4%BC%BC%E5%BA%A6/17509249?fr=aladdin

 

6. RNN长序列语言模型(2010年)

0x1：传统ngram统计语言模型和NNLM语言模型的局限

ngram词频统计语言模型的问题在于捕捉句子中长期依赖的能力非常有限，目前在工业界的使用范围已经比较小，ngram词频统计模型的意义主要在于学术研究。

改进后的NNLM引入了神经网络结构，通过隐藏层的的线性/非线性变换得到一定的抽象表征能力，但是本质上就是使用神经网络编码的n-gram模型，而且对输入数据要求固定长度(一般取5-10)，因为本质上遵从了Markov Assumption，所以同样也无法解决长期依赖的问题。 

RNN长序列语言模型的提出，主要就是为了解决如何学习到长距离的依赖关系的问题。

0x2：Recurrent Neural Networks Pipeline

新的语言模型是利用RNN对序列建模，复用不同时刻的线性非线性单元及权值，理论上每一步 t 预测的单词，依赖于 t 之前所有的单词。

给定一个词向量序列，序列按照时间点 t 逐个输入，每个时间点都会得到一个对应的输出

在时刻 t 时输出的整个词表 |V| 上的概率分布，是给定上文和最近的单词预测的下一个单词。其中

隐藏层神经元的特征表示：

：是时间 t 时输入的单词的词向量。

：输入词向量的的权值矩阵。

：前一个时间节点隐藏层特征表示的权值矩阵。

：前一个时间点 t−1 的非线性激活函数的输出。

σ()：非线性激活函数(sigmoid)。

关于RNN神经网络的更多讨论，可以参阅另一篇blog。

0x3：RNN语言模型

回顾一下最本质的语言模型（language model）

总结一句话：通过联合概率和条件概率的形式来数值化定义一段文本序列的似然概率。

在ngram词频统计语言模型中，通过词频统计的方式进行贝叶斯条件概率计算，得到似然条件概率值，例如著名的朴素贝叶斯算法。同时因为保存了词汇表，因此可以得到每个文本序列的词向量表示（向量空间由词表决定），这算一个副产品；

在NNLM语言模型中，通过神经网络的线性/非线性转换以及激活函数（例如softmax）得到似然条件概率值。同时因为保存了隐层的系数矩阵，因此可以得到每个文本序列以及每个词的词向量表示（向量空间维数由开发者指定），这算一个副产品；

在RNN语言模型中，通过循环神经网络的隐状态神经元以及激活函数得到似然条件概率。同时因为每一个输入词x都会得到一个对应的输入y，因此可以得到每个文本序列的词向量表示（向量空间由词表决定），这算一个副产品。只是大部分时候我们不太关注这个词向量，对于RNN语言模型，我们多数时候用到的是它的序列预测能力；

Relevant Link:  

https://www.cnblogs.com/LittleHann/p/6627711.html
http://www.hankcs.com/nlp/cs224n-rnn-and-language-models.html
https://www.cnblogs.com/rocketfan/p/5052245.html 

 

7. word2vec语言模型（CBOW&Skip-gram）(2013年)

0x1：word2vec提出的历史背景 - 传统NNLM语言模型存在的问题

学术研究就是在不断提出问题和解决问题的螺旋中前进，Bengio在提出NNLM模型后，大家发现NNLM存在几个问题：

1. 一个问题是，同Ngram模型一样，NNLM模型只能处理定长的序列。在03年的论文里，Bengio等人将模型能够一次处理的序列长度N提高到了5，虽然相比bigram和trigram已经是很大的提升，但依然缺少灵活性。因此，Mikolov等人在2010年提出了一种RNNLM模型，用递归神经网络代替原始模型里的前向反馈神经网络，并将Embedding层与RNN里的隐藏层合并，从而解决了变长序列的问题；
2. 另一个问题就比较严重了。NNLM的训练太慢了。即便是在百万量级的数据集上，即便是借助了40个CPU进行训练，NNLM也需要耗时数周才能给出一个稍微靠谱的解来。显然，对于现在动辄上千万甚至上亿的真实语料库，训练一个NNLM模型几乎是一个impossible mission；

Mikolov发现，原始的NNLM模型的训练其实可以拆分成两个步骤：

1. 用一个简单模型训练出连续的词向量；
2. 基于词向量的表达，训练一个连续的Ngram神经网络模型。而NNLM模型的计算瓶颈主要是在第二步，简单说就是其计算量仍过大，主要计算量集中在非线性层h和输出层z的矩阵W,U运算和softmax计算；

word2vec的主要思想就是：既然我们只是想得到word的连续特征向量，完全可以对第二步里的神经网络模型进行简化。

Mikolov在2013年推出了两篇paper，并开源了一款计算词向量的工具，word2vec。

他对原始的NNLM模型做如下改造：

1. 移除前向反馈神经网络中非线性的hidden layer，直接将中间层的Embedding layer与输出层的softmax layer连接；
2. 忽略上下文环境的序列信息（没有隐层对接上下文环境的词序列）：输入的所有词向量均汇总到同一个Embedding layer；
3. 将future words（当前词的前序和后序字符）都纳入上下文环境

0x2：word2vec语言模型结构

严格来说，word2vec不是一个具体的语言模型，它是2013年Google团队发表的一个。word2vec工具主要包含两个模型：跳字模型（skip-gram）和连续词袋模型（continuous bag of words CBOW），以及两种高效训练的方法：负采样（negative sampling）和层序softmax（hierarchical softmax）。

平时业内大家交流时直接简称都叫word2vec了，并没有什么太大问题，读者朋友只要知道这点即可。

1. CBoW模型（Continuous Bag-of-Words Model）

CBOW的思想是从一个词序列中抠掉一个词，用这个词的上下文去预测这个词。

整体架构逻辑图如下：

 

注意输入层中词序列输入的时刻 t 前序和后序的词。 

数据结构图如下：

 

1）输入层

输入层和NNLM没有太大区别，本质上还是一个ngram序列。

上下文词序列以onehot形式输入，单词向量空间dimension为V，上下文单词个数为C。

2）隐藏层 - embedding layer

输入序列的所有onehot分别乘以共享的输入权重系数矩阵W（V*N矩阵，N为自己设定的词嵌入向量维度）。矩阵W就是最终训练结束后得到的词向量矩阵，也叫做word vector look-up table。

所得的向量相加求平均作为隐层向量（相加求平均提高了网络的计算性能），size为1N。所以有些paper上把这层也叫projection layer，理解意思即可。

3）输出层，

乘以输出权重矩阵W'（N*V），得到向量（1V）。输入激活函数处理得到V-dim概率分布，每一维代表一个单词的似然概率。

概率最大的index所指示的单词为预测出的中间词（target word）与true label的onehot做比较，进行反向反馈训练。

2. Skip-gram模型

Skip-Gram模型和CBOW的思路是反着来的，即输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。

1）输入层

和CBow是一样的，区别在于单词数为1。

2）隐藏层 - embedding

3）输出层

上下文context的序列长度由开发者通过skip_window参数指定。

例如我们设定skip_window=2代表着选取左input word左侧2个词和右侧2个词进入我们的窗口，所以整个窗口大小span=2x2=4。

即已知${\mathrm{，预测出现的对数似然函数为}}^{}$

通过softmax取前max的context序列，之后和目标值进行对比，计算损失并反向梯度反馈。

举一个Skip-gram的例子说明上述过程：

我们选定句子“The quick brown fox jumps over lazy dog”，设定我们的窗口大小为2（window_size=2），也就是说我们仅选输入词前后各两个词和输入词进行组合。下图中，蓝色代表input word，方框内代表位于窗口内的单词。Training Samples（输入， 输出）

3. CBow和Skip-gram的优点

这两种方式与NNLM有很大的不同，NNLM的主要任务是预测句子概率，词向量只用到了上文信息，是其中间产物。

word2vec是为获得单词的分布式表征而生，根据句子上下文学习单词的语义和语法信息。除了网络结构更加结合上下文信息, word2vec的另一大贡献在计算优化上。word2vec去掉了非线性隐层,CBOW将输入直接相加通过softmanx进行预测，减少了隐层的大量计算，同时通过分层softmax (hierarchical Softmax)和负采样(Negative sampling)对softmax的计算也做了很大优化。

0x3：Hierarchical Softmax

1. 为什么会提出hierarchical softmax

原始的word2vec模型从隐藏层到输出的softmax层的计算量很大，因为要计算所有词的softmax概率，再去找概率最大的值。这个模型如下图所示。其中V是词汇表的大小。

为此，Mikolov引入了两种优化算法：层次Softmax（Hierarchical Softmax）和负采样（Negative Sampling），我们接下来逐个讨论。

笔者思考：本质上，h-softmax解决的问题是“Massive multi-label（海量多分类）”的问题，当待分类或待预测的label数量很多时，利用二叉树这种数据结构，可以将O(N)的复杂度显著降低到O(logN)的对数复杂度，大大提高运算效率。

2. 通过二叉二叉霍夫曼树代替输出层神经元

与传统的神经网络softmax输出不同，为了避免要计算整个词表每一个词的softmax概率，word2vec的hierarchical softmax结构把输出层改成了一颗Huffman树。

1）图中叶子节点

图中白色的叶子节点表示词汇表中所有的 |V| 个词，Huffman树并没有改变整个模型的基础架构，对于输出层来说，每一个词依然会有一个对应的似然概率计算路径。

接下来我们讨论在神经网络训练过程中，是如何调整Huffman树节点对应的权重系数的。

2）图中黑色非叶子节点

Huffman树中每一叶子结点代表一个label，在每一个非叶子节点处都需要作一次二分类，走左边的概率和走右边的概率，这里用逻辑回归（sigmoid函数）的公式表示：

向左走（正类）：

向右走（负类）：

其中 xi 是当前节点中的词向量，θ 是要学习的模型参数。

3）计算输入条件概率

每一个叶子节点都对应唯一的一条从root节点出发的路径，以上图为例，当我们计算${\mathrm{w2输出概率时，我们需要从根节点到叶子结点计算概率的乘积。}}^{}$

4）更新路径上节点的权重向量

我们的目的是使得$\mathrm{这条路径的概率最大，即最大。}$

$\mathrm{通过累乘路径上所有节点的似然概率公式，然后通过随机梯度上升进行BP反馈，不断}$更新从根结点到${\mathrm{叶子结点的路径上面节点的向量即可，而不需要更新所有的词的出现概率，这样大大的缩小了模型训练更新的时间。}}^{}$

0x4：Negative Sampling

1. 为什么会提出Negative sampling

在NNLM和word2ve的方法输出层的维度均为词表大小$|V|，从而输出权重矩阵为dim \times |V|，矩阵高维稀疏。$

在训练神经网络时，每当接受一个训练样本，然后调整所有神经单元权重参数，来使神经网络预测更加准确。换句话说，每个训练样本都将会调整所有神经网络中的参数，非常耗时。

$回到语言模型训练的核心任务，当训练一个样本时，我们主要目标是让预测这个训练样本（正样本）更准，对负样本只需要进行微调即可。最终让正负样本在概率空间有足够的区分性。$

$negative\; sampling的核心思想就是：每次让一个训练样本仅仅更新一小部分神经元的权重参数，从而显著降低梯度下降过程中的计算量。$

举一个例子，如果 vocabulary 大小为1万时， 当输入样本 ( "fox", "quick") 到神经网络时， “ fox” 经过 one-hot 编码，在输出层我们期望对应 “quick” 单词的那个神经元结点输出 1，其余 9999 个都应该输出 0。

在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们为 negative word candidate set，即可能成为Negative sampling selection的候选词。

negative sampling 的具体做法是 ，将根据词频正序排列选择一定数量的 negative words，比如选 10个 negative words 来更新对应的权重参数。

在论文中作者指出指出对于小规模数据集，建议选择 5-20 个 negative words，对于大规模数据集选择 2-5个 negative words.

如果使用了 negative sampling 仅仅去更新positive word- “quick” 和选择的其他 10 个negative words 的结点对应的权重，共计 11 个输出神经元，相当于每次只更新 dim x 11 个权重参数。对于 dim * |V| 的权重来说，计算效率就大幅度提高。

2. Negative Sampling负采样方法说明

接下来讨论具体的 negative word 是根据什么标准选出来的。

负采样的选择利用带权采样，即根据出现概率来选，经常出现的词更容易被选为负例样本。公式如下

这里的$\mathrm{0.750.75是一种平滑策略，让低频词出现的机会更大一些。}$

Relevant Link:  

https://rare-technologies.com/word2vec-tutorial/
https://arxiv.org/pdf/1301.3781.pdf
https://arxiv.org/pdf/1310.4546.pdf
https://www.jianshu.com/p/471d9bfbd72f
https://radimrehurek.com/gensim/models/word2vec.html
http://www.cnblogs.com/pinard/p/7160330.html
https://www.cnblogs.com/guoyaohua/p/9240336.html
https://www.cnblogs.com/eniac1946/p/8818892.html
http://www.cnblogs.com/pinard/p/7160330.html
https://blog.csdn.net/itplus/article/details/37969979
http://www.cnblogs.com/pinard/p/7249903.html
https://www.jianshu.com/p/ed15e2adbfad

 

8. GloVe（Global Vectors for Word Representation）(2014年)

正如原始论文的标题而言，GloVe的全称叫Global Vectors for Word Representation，顾名思义，它是一个基于全局词频统计（count-based & overall statistics）的词表征（word representation）模型。

0x1：GloVe的语言模型假设

1. Glove依然符合基本语言假设范畴

Glove在语言模型的表征上做了很多的创新，但我们学习它也应该认识到，其本质并没有跳出语言模型的核心范畴。

语言模型的核心任务用一句话概括就是：将一段词序列（一段文本、基因序列、音频序列），表示为所有词（文字、单基因碱基对、单波峰音频）和其所在上下文（可以是前序/后序/双序）组合，的条件概率的累乘，即联合条件概率。文本存在即概率，万物存在皆有概率。

具体用公式表示如下：

2. Glove对原有提出的语言模型的继承与发展

各个语言模型的区别就在于计算得到这个条件概率。我们来回顾一下文章此前讨论的语言模型：

1. Ngram Frequency Aspect Language Model：P（wi | wj）= Count(wi,wj) / N：
直接统计所有ngram词序列出现的频率作为概率值，这是频率派的观点，即在大数据情况下，频率统计 = 概率真值。在这个基础上，有一些衍生的所谓平滑方法，本质是加入了一些先验因子，用极大后验概率统计代替极大似然统计，但是这些不重要，读者朋友要理解的是其核心思想，即频率派思维；

2. Neural-Network Likelihood Function Aspect：
NNLM、RNN、word2vec各自的细节有区别，笔者这里概括如下：
input(Central words，单个词/词序列) word vector -> 
Neural-Network -> 
Likelihood Function（softmax）-> 
output(most likely context words) = 极大后验概率估计得到可能性最大的context上下文词/词序列) -> 
Loss Function(基于预测结果和目标结果的diff计算损失) -> 
BP反向调整神经网络的参数；

基本上来说，Glove和上述两种模式都不太一样，Glove综合了频率统计特征、高维隐神经元表征词向量、和Ngram滑动窗口思想，Glove提出了Ngram窗口用词共现矩阵(word-word  co-occurrence matrix) 的方式来提取和表征语料的词法和语义。

Glove语言模型的基本假设可以概括为：基于Ngram滑动窗口，彼此相似的词，相比于彼此不相似的词，在窗口中共同出现的概率要更高，语义的相似性可以通过窗口共现概率来体现。

这样解释还是非常抽象，下个章节，我们从词共现窗口这个概念开始讨论起，逐渐抽丝剥茧。

0x2：Window based co-occurrence matrix（基于窗口的共现矩阵）

在开始讨论Glove的算法原理之前，我们先从一个简单的例子开始，讨论一下什么是共现矩阵。

1. 一个Unigram-co-occurrence matrix的简单例子

ngram窗口长度这里选择为1，即unigrame，矩阵具有对称性（与在左侧或右侧无关）。样本数据集包含3段sentence：

1. I like deep learning.
2. I like NLP.
3. I enjoy flying.

得到如下词共现矩阵，统计的方法是统计所有的ngram滑动窗口中，每个中心词和和其他背景词出现次数的累加和：

例如上图中，我们看到第二行第一列，“I”和“like”的共现词频统计结果为2，这是因为在训练预料中，“I”和“like”这2个词在所有ngram滑动窗口中，共同出现了2次。

1）我们能否直接基于共现矩阵本身直接得到词向量表示呢？

我们已经基于训练预料得到一个词共现矩阵了，是不是直接就已经得到词向量表示了呢？答案是肯定的！

bow onehot编码 - 统计视角

有了词共现矩阵，每个词的向量就可以表示出来了，词频本身也是语言规律的一种体现。比如上图图1中，“I”就是对应第一行的向量，所以在这个模型中，I的向量表示就是 (0,2,1,0,0,0,0,0)或(0,2,1,0,0,0,0,0)，其他的类推。

但是onehot词向量编码存在一些固有的问题，熟悉ngram词袋语言模型的同学应该非常熟悉了：

1. 随着词汇增多，词汇表会随之增大，词向量的大小会变得很大；
2. 每个词向量都非常高维，需要大量存储空间；
3. 随之产生的的分类模型具有稀疏性的问题。因为维数高，又稀疏，模型分类不易
4. 模型不够健壮（robust）

那这个想法不行，我们换一个。

Singular Value DecomposiRon（SVD，奇异值分解）- 降维视角

既然onehot直接编码的词向量空间太大了，那一个很自然的改进想法就是，找一个低维向量(Low dimensional vectors)来替代原始的onehot向量。

这种方案的想法是：将“大多数”的重要信息保存在一个固定的、数量较小的维度的向量。通常这个维度是25-1000维。

如文章前面所讨论，可以采用SVD矩阵奇异值分解的方法，找到一个和原始词向量矩阵近似的低阶矩阵。

但是SVD（奇异值分解）依然有以下几个问题：

1. 计算代价太大。对于一个n*m的矩阵，计算复杂度是O(mn2)O(mn2)。这就导致会与数百万的文档或词汇不易计算；
2. 难以将新的词汇或文档合并进去，这在工程项目中是很要命的，在大量业务场景中，时刻都会有新的语料输入，我们可能会需要定期对模型进行重新训练，采用SVD方案，意味着每当输入一些当前词汇表中不存在的新词，整个SVD过程就要重新来一遍；

这两个想法都不行，那问题出在哪呢？其实仔细思考后就会发现，这2个想法的问题和ngram词袋模型都一样，都是信息冗余度太高了，没有有效地利用低阶近似这个逼近原理，虽然SVD是在做matrix projction，但是因为矩阵运算天然的巨大运算量，实际场景难以使用。

其实NNLM的思想是非常跨时代的，NNLM并不是像SVD那样要直接对原始的信息矩阵进行降维（正面硬扛），而是引入了极大似然估计的思想，通过神经网络的隐层来构建出一个新的词向量空间，通过极大似然估计不断训练迭代，使这个词向量空间不断逼近我们的目标信息矩阵。

2. Glove 2-gram word-co-occurrence matrix

看另一个例子，对于句子“我老爱我老婆了”，滑动窗口大小设定为2，则得到以下共现概率矩阵

假设词表大小为$\mathrm{V，共现矩阵X大小则为 [V, V]}$：

• 表示单词 j 出现在单词 i 的上下文中的次数；
•  表示单词 i 的上下文中所有单词出现的总次数，即，它可以理解为一个边缘概率；
• ，即表示单词 j 出现在单词 i 的上下文中的概率占比（局部和整体的比率），这个比率值越大，说明 i 和 j 的词组合在语料库中出现的频率越高，即说明 i 和 j 非常可能很接近，原理上有点类似TF-IDF的局部与全局思想。

3. 词共现矩阵具备语法/语义表征能力吗？

原论文中，作者举了一个例子，很直观地说明了，词共现矩阵是一种非常有效地语法/语义表征方式。

假定我们关心两个中心词，i和j。其中，我们假定i=ice，j=steam。

我们知道，ice和solid更有关，而steam和solid关系相对就不是那么大。具体到底谁更相关呢？通过对比两个条件概率的比率，可以很清楚的看到这种相关度差距有多大，差距越大，区分度就越明显。在第一列中，P(k|ice) / P(k|steam)的比例就高达10，说明区分度是比较明显的。

同样，其他条件组合也是一样，读者朋友可以逐一审阅。

这样，我们就已经得到了所有词序列组合的条件概率了，并且也确信它的确非常有效，这很棒！泡杯咖啡。接下来的任务是构建一个新的词向量空间，来逼近拟合我们已知的条件概率。

0x3：词向量相似性推导 

构建词向量（Word Vector）和共现矩阵（Co-ocurrence Matrix）之间的近似关系，论文的作者提出以下的公式可以近似地表达两者之间的关系：

代表两个单词向量的向量乘积，即表示向量间的余弦相似度。上面解释过了，是一个概率比率。这里隐含的假设是，越相似的单词越有可能大量在ngram滑动窗口中共同出现。

两边同时取对数可得：

逼近损失计算公式为：

通过最小化平方损失函数可得损失函数的原始形式：

同时，我们知道词共现矩阵 V $\mathrm{是一个对称矩阵，单词和上下文单词其实是相对的，即\; i\; 和\; j\; 向量是可以互换位置而不影响最终结果的。}$

但是我们发现上述原始损失函数等号右侧的$\mathrm{的存在，导致损失函数是不满足对称性（symmetry）的，而且这个其实是跟\; |V|\; 是独立的，它只跟 i 有关，它可以理解为边缘分布，利用偏置项 bi，bj 代替,。}$

$\mathrm{于是得到一个新的对称性损失函数：}$

到了这一步，还没有结束，还有最后一个问题，论文作者为了更好地表征真实情况的语言规律，又增加一个约束函数，即：

下面来解释 f(Xij)

我们知道在一个语料库中，肯定存在很多单词他们在一起出现的次数是很多的（frequent co-occurrences），那么我们希望能对损失函数增加几个约束条件（constraint）：

• 1. 高频单词的权重要大于那些很少在一起出现的单词（rare co-occurrences），所以这个函数要是非递减函数（non-decreasing）；
• 2. 但我们也不希望这个权重过大（overweighted），当到达一定程度之后应该不再增加；
• 3. 如果两个单词没有在一起出现，也就是 ${\mathrm{，那么他们应该不参与到loss\; function的计算当中去，也就是f(x)要满足f(0)=0}}^{}$

满足以上两个条件的函数有很多，作者采用了如下形式的分段函数：

f(x)起到对每个词重新分配一个权重的作用，函数图像如下所示：

${\mathrm{和 \alpha 为手动设定的阈值，glove给出的经验值 \alpha =3/4，，论文作者在它的数据集上表现的非常好，我们在自己的项目中也可以根据实际情况调整，实际上，笔者从实践中发现，可以根据数据集的实际情况动态计算得到，它本质上是起到归一化的作用。}}^{}$ 

值得注意的是，这种思想也是机器学习中一个非常常见的思想，用一个概率分布去拟合另一个概率分布，属于生成式模型的一种。

0x4：Glove的简单使用

在这里可以找到论文作者基于维基百科及推特还有其他数据集分别训练的多个GloVe模型，可以下载下来，解压缩，使用gensim工具包进行使用。

我们这里使用已经训练好的模型，查看Glove对寻找相似词的能力：

# -*- coding: utf-8 -*-


from gensim.test.utils import datapath, get_tmpfile
from gensim.models import KeyedVectors
from gensim.scripts.glove2word2vec import glove2word2vec



if __name__ == '__main__':
    # 输入文件
    # http://nlp.stanford.edu/data/glove.840B.300d.zip
    glove_file = './glove.840B.300d.txt'
    # 输出文件
    tmp_file = get_tmpfile("test_word2vec.txt")

    # call glove2word2vec script
    # default way (through CLI): python -m gensim.scripts.glove2word2vec --input <glove_file> --output <w2v_file>

    # gensim库添加了一个模块，可以用来将glove格式的词向量转为word2vec的词向量，这样，我们就可以完美的用gensim加载glove训练的词向量了
    glove2word2vec(glove_file, tmp_file)

    # 加载转化后的文件
    model = KeyedVectors.load_word2vec_format(tmp_file) 
     
    # 获得单词cat的词向量
    cat_vec = glove_model['cat']
    print(cat_vec)
    # 获得单词frog的最相似向量的词汇
    print(glove_model.most_similar('frog'))

查看前3个相似词：

可以看到，Glove能够表达出一些词相似性，但是也受到训练预料的影响，存在一定的误差。

Relevant Link:   

https://nlp.stanford.edu/projects/glove/
https://medium.com/m/global-identity?redirectUrl=https%3A%2F%2Ftowardsdatascience.com%2Femnlp-what-is-glove-part-i-3b6ce6a7f970
https://en.wikipedia.org/wiki/GloVe_(machine_learning) 
http://www.fanyeong.com/2018/02/19/glove-in-detail/#comment-2190 
https://zhuanlan.zhihu.com/p/50946044 
https://nlp.stanford.edu/pubs/glove.pdf
https://zhuanlan.zhihu.com/p/42073620 

 

9. ELMo语言模型（Embedding from Language Model）(2018年)

0x1：历史原有语言模型遇到的新挑战及其思考

Glove/Word2vec在NLP领域受到新挑战是”多义词问题“，多义词是自然语言中经常出现的现象，也是语言灵活性和高效性的一种体现。

比如根据不同的上下文，苹果可能指手机，也可能指水果。

但是在用传统语言模型训练的时候，不论什么上下文的句子经过word2vec/glove，都只能得到苹果的一个静态词向量表达，所以word embedding无法区分多义词的不同语义，这就是它的一个比较严重的问题。

那该如何去思考解决的方向呢？让我们回到一个NLP语言模型的核心任务上来，泛化地说，一个NLP语言模型必须要完成如下几个目标：

（1）对词具备编码能力；
（2）capture syntactic and semantic information of words: 有效表征对应语言的语法和语义特性，也即对不同的语法和语义要在编码上能够区分；
（3）context-dependent: 对语言中包含的上下文多态性，也即多义词要具备编码能力，也即对不同上下文环境下的词在编码上能够区分；

以上3点，传统模型完成可以胜任前2点，但是第3点对模型提出了更高的复杂性要求。这给了我们几个启发式地思考方向：

1. 要引入更深的神经网络来存储和表征这部分新的信息；
2. bidirectional RNN/LSTM网络，能够捕获单词所在的不同上下文环境信息；
3. 使用多层双向循环神经网络结构，能够提取不同层次的语言信息，较低层的LSTM抓住的是词汇的简单句法信息（也就是我们所谓的多义词），较高层次的LSTM向量抓住的是词汇的语义信息（上下文无关的语言信息）。关于这点，我们从CNN的不断层次的卷积核代表不同层次的图像细节也可以得到类似的启发；

0x2：ELMO网络整体结构

整体上，ELMo包括预训练+微调两个阶段，如下图所示：

1. 预训练（pre-train unsupervised）：
无监督的语法/语义学习，主要用于提取词的语法/语义/上下文信息。
无监督的语言模型起到encoder的作用，将词转换为词向量，之后作为输入进入另一个有监督的语言模型中。这种架构目前被学术界和工业界大量接受并采用。
同时，这种架构也是一种迁移学习（Transfer learning model）的思想，即通过预训练一种泛化能力较好的网络模型，并将网络的输出作为下游特定任务模型的输入进行有监督训练；

2. 微调（fine-tune supervised task model）：
有监督NLP任务模型，主要用于根据特定标签数据，针对special task，对词向量进行特定性的调整；

1. 输入层 - embedding

ELMo在embedding层得到基础的词向量表示。

2. 双向双层LSTM网络

这个网络结构是ELMO和主要核心，论文花了大量的篇幅对这个话题展开了讨论，我们这里介绍其主要的思想。

1）Bidirectional language models

讨论双向语言模型前，我们再来回顾下我们传统的标准语言模型，也叫前向语言模型（forward language model）。

给定一个包含N个token的序列(t1, t2, ..., tN)，计算每个词(tk)以及这个词的前序子序列(t1, ..., tk−1)的条件概率累积和：

不管前面介绍的语言模型如何复杂，本质上都没有跳出这个语言模型的范畴。直到 Bidirectional language models 被提出(2016)。

双向LSTM网络如下图所示：

biLM在大数据集上利用语言模型任务，根据单词${\mathrm{的上下文去正确预测单词。}}^{}$

${\mathrm{图中左侧部分LSTM的输入是的上文，右侧部分LSTM的输入是的下文，模型参数共享输入Embedding层和Softmax层，目标函数为：}}^{}$

2）two-layer LSTM

论文作者通过分析lowest和top layer中词向量在空间聚集性上的表现，发现不同层次的layer，提取出了不同的语言信息：

1. 较低层的LSTM抓住的是词汇的简单句法信息（也就是我们所谓的多义词）；
2. 较高层次的LSTM向量抓住的是词汇的语义信息（上下文无关的语言信息）；

这个实验读者朋友自己通过t-SNE可视化来得到。

3. Linear combination of the biLM layers

上个章节说道，不同层次的LSTM捕获到了不同层次的语言信息。ELMO模型通过线性组合，将所有LSTM层组合起来(projection)，获得了一个更好的性能。

在线性组合层中，ELMO通过归一化加权，将biLM转换成一个向量输入到下游任务中。

4. 下游任务（special task NLP model）

这一层可以是任意有监督网络结构。

Relevant Link:    

https://arxiv.org/pdf/1802.05365.pdf

 

10. GPT(Generative Pre-Training)(2018年)

2018年提出的GPT，全称是生成式的预训练，它是一种基于多层transformer的单向语言模型。GPT总体包括两个阶段：首先利用其语言模型的特性在海量语料库上进行预训练；完成预训练后，通过fine-tune的模型解决下游任务。如下图所示，GPT可以用于丰富的任务类型

GPT与ELMo很像，区别主要在于

1. 使用transformer取代LSTM对特征进行抽取。Transformer是当前NLP领域最强的特征抽取器，可以更加充分地提取语义特征。
2. 坚持使用单向语言模型。ELMo的一个显著特点是利用上下文信息对词向量进行表征，而GPT使用的是单向语言模型，仅使用上文信息对下文进行预测。这种选择比较符合人类的阅读方式，同时也有一定的局限性，如阅读理解中，我们通常需要结合上下文才能进行决策，仅考虑上文会使预训练丢失掉很多信息量。(注：这一点会在BERT中进行优化。)
3. GPT预训练后的使用方式也与ELMo不同，ELMo属于基于特征的预训练方式，而GPT在完成预训练后需要进行finetune（类似于图像中迁移学习的方式）

Relevant Link: 

11. BERT(2018年)

ELMo通过双向拼接融合词向量表征上下文，GPT利用单向语言模型来获取向量表达，2018年提出的BERT对GPT的改进有点借鉴于NNLM到CBOW的改进，将任务从预测句中下一个词变为从句子中抠掉一个词用上下文去预测这个词，同时增加了预测是否是下一个句子的任务。模型结构沿用GPT的思想，利用transformer的self-attentnion和FFN前馈网络叠加，充分利用transformer强大特征抽取能力

相比GPT在微调时需要加入起始符、终结符和分隔符等改造，BERT在训练时就将其加入，保证预训练和微调的输入之间没有差异，提高预训练的可利用性。
BERT是对近几年NLP进展（特征抽取器、语言模型）的集大成者，充分利用大量的无监督数据，将语言学知识隐含地引入特定任务。

Relevant Link: 

12. GPT-2(2019年)

2019年提出的GPT-2文本生成的效果十分惊艳。这里对GPT-2进行简单的讨论，主要关注其优化点。

1. 对数据质量进行筛选，使用更高质量的数据
2. 数据的选取范围更广，包括多个领域
3. 使用更大的数据量
4. 加大模型，增加参数（15亿参数），是BERT large（3亿参数）五倍的参数量，两倍的深度，这里体现出深层神经网络的强大表达能力
5. 对transformer网络结构进行微调如下：调整layer-norm的位置，根据网络深度调整部分初始化，调整部分超参
6. 如论文名称Language Models are Unsupervised Multitask Learners（无监督多任务学习器，这个标题非常好地解释了语言模型的本质），GPT-2更加强调了语言模型天生的无监督和多任务这两种特性，这也是当前NLP领域最显著的两个趋势。

直观上而言就是GPT-2使用更多更优质更全面的数据，并增加模型的复杂度。除此以外，GPT-2其实还蕴含了很多深意，值得进行深入研究。

Relevant Link: 

http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/Attain%20(v3).pdf