南京大学 静态软件分析（static program analyzes）-- Interprocedural Analysis 学习笔记

一、Motivation of Interprocedural Analysis

在实际的程序中方法调用非常常见，那么我们如何分析带方法调用的程序呢？

最简单的处理方式是（这里仍然以常量传播作为一个例子）：做最保守的假设，即为函数调用返回NAC。而这种情况会丢失精度。

如果使用过程内分析最safe的的处理方式，下图中的n和y分析结果都不是常量，尽管我们能够一眼看出他们的运行时值是n=10，y=43。

通过引入过程间分析能够提高精度。

 

二、Call Graph Construction (CHA)

接下来我们讨论一个必要的数据结构Call Graph（调用关系图）。

Definition of Call Graph

A representation of calling relationships in the program

• Essentially, a call graph is a set of call edges from call-sites to their target methods (callees)

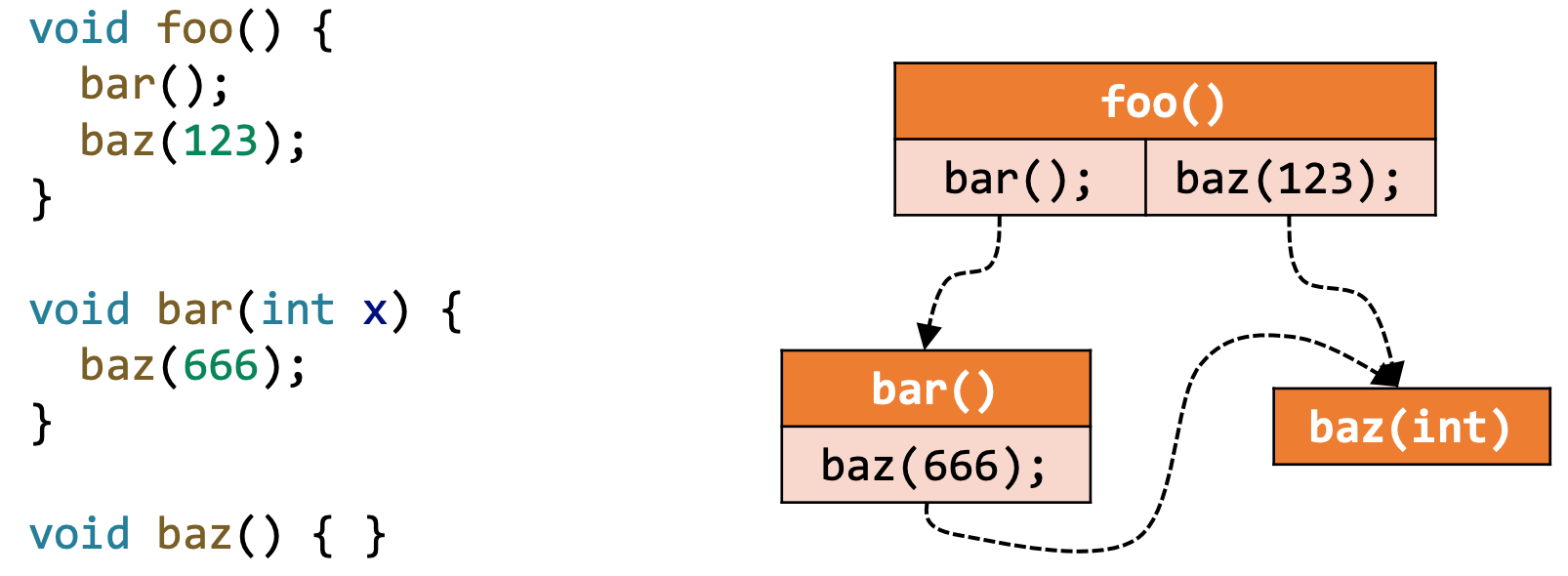
Call Graph的应用场景：

• Foundation of all interprocedural analyses
• Program optimization
• Program understanding
• Program debugging
• Program testing
• And many more …

Call Graph Construction for OOPLs（focus on Java）

Call Graph有很多种不同的构造方法，我们接下来会讲解两个极端：最准确的和最快速的。

Call types in Java

本课主要关注Java的调用关系图构建。为此，我们需要先了解Java中调用的类型。Java中call可分为三类：

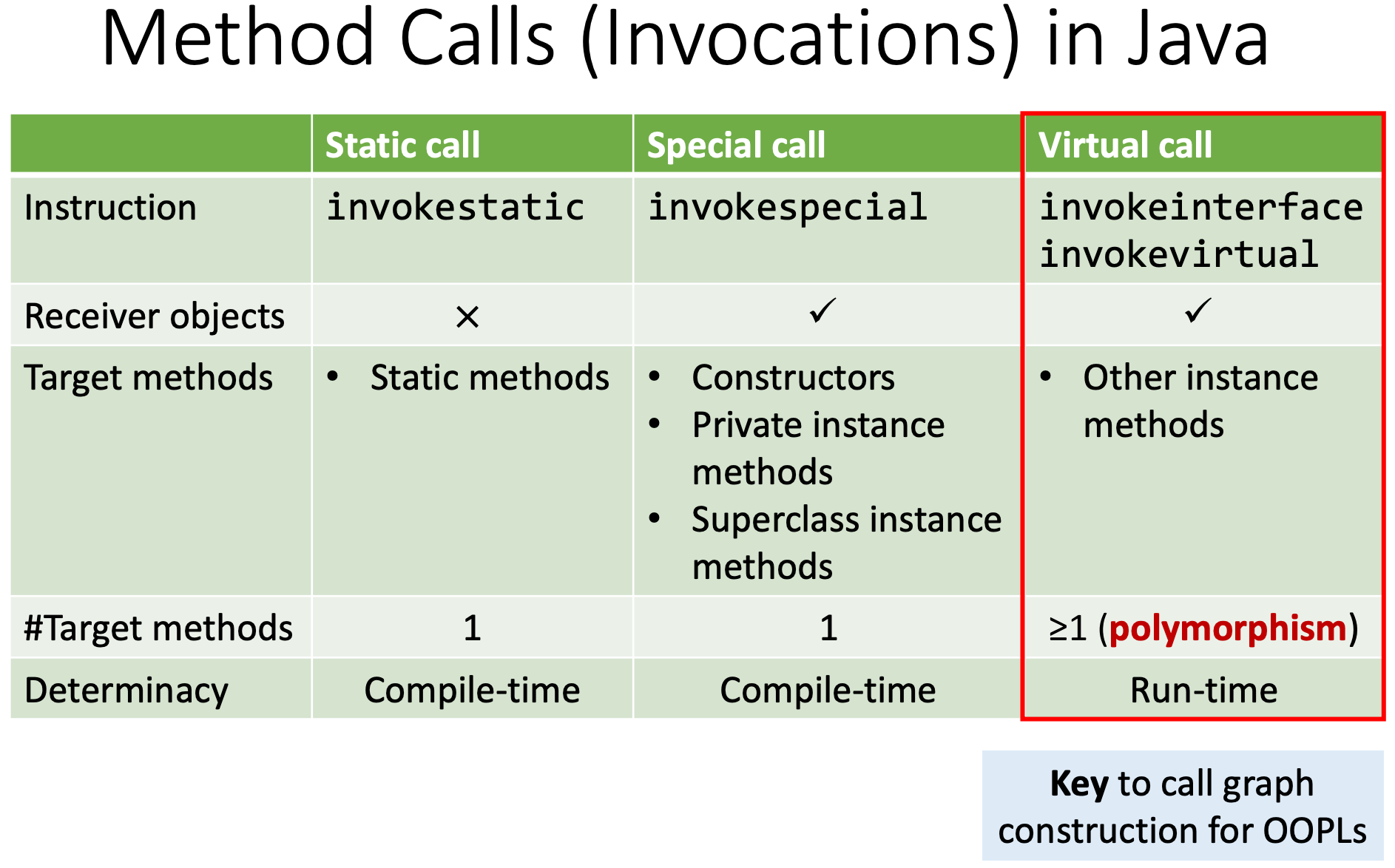
• Instruction：指Java的IR中的指令
• Receiver objects：方法调用对应的实例对象（static方法调用不需要对应实例）
• Target methods：表达IR指令到被调用目标方法的映射关系
• Num of target methods：call对应的可能被调用的目标方法的数量。Virtual call与动态绑定和多态实现有关，可以对应多个对象下的重写方法。所以Virtual call的可能对象可能超过1个
• Determinacy：指什么时候能够确定这个call的对应方法。Virtual call与多态有关，只能在运行时决定调用哪一个具体方法的实现。其他两种call都和多态机制不相关，编译时刻就可以确定

Method Dispatch of Virtual Calls

由于多态和receiver在静态分析时不能确定的原因，java的Virtual call的实际调用函数需要在运行代码时确定，在静态分析时是无法确定其准确值的。在动态运行时，Virtual call基于两点决定调用哪个具体方法： 

• type of the receiver object (pointed by o)：c
  • 
• method signature at the call site：m。In this lecture, a signature acts as an identifier of a method
  • Signature = class type + method name + descriptor
  • Descriptor = return type + parameter types

We define function Dispatch(𝑐, 𝑚) to simulate the procedure of run-time method dispatch

Dispatch: An Example

在实际执行时，需要根据调用的对象和调用的方法来找到最终调用的实际函数。举一个例子说明如何采用Dispatch的方式进行查找。

在这个例子中，

• x.foo()的receiver是x，receiver type是B，因为在class B中找不到和方法调用同名的非抽象方法声明，因此继续搜索class B的父类，即class A，因此dispatch结果为A.foo()
• x.foo()的receiver是x，receiver type是C，因为在class C中找到了和方法调用同名的非抽象方法声明，因此dispatch结果为C.foo()

Class Hierarchy Analysis* (CHA)：Call Graph Construction的关键环节

 

Definition of CHA

• Require the class hierarchy information (inheritance structure) of the whole program
  • 需要首先获得整个程序的类继承关系图
• Resolve a virtual call based on the declared type of receiver variable of the call site
  • 通过接收变量的声明类型来解析Virtual call
  • 接收变量的例子：在a.foo()中，a就是接收变量
  • 
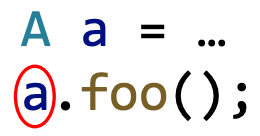
• Assume the receiver variable a may point to objects of class A or all subclasses of A（Resolve target methods by looking up the class hierarchy of class A）
  • 假设一个接收变量能够指向A或A的所有子类

Call Resolution of CHA

总结一下CHA算法，

Algorithm of Resolve

We define function Resolve(𝑐𝑐𝑠𝑠) to resolve possible target methods of a call site 𝑐𝑐𝑐𝑐 by CHA

• call site(cs)就是调用语句，m(method)就是对应的函数签名。
• T集合中保存找到的结果
• 三个if分支分别对应之前提到的Java中的三种call类型
  • Static call(所有的静态方法调用)
  • Special call(使用super关键字的调用，构造函数调用和Private instance method)
  • Virtual call(其他所有调用)

Static call 

具体来说，静态方法调用前写的是类名，而非静态方法调用前写的是变量或指针名。静态方法调用不需要依赖实例。 

Special call

Superclass instance method（super关键字）最为复杂，故优先考虑这种情况

为什么处理super调用需要使用Dispatch函数？

在下图所示情况中没有Dispatch函数时无法正确解析C类的super.foo调用： 

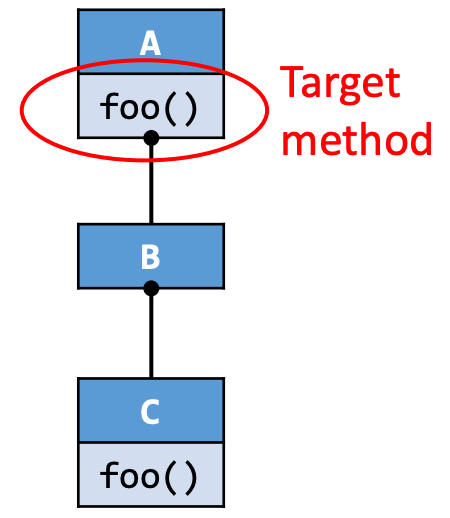
而Private instance method和Constructor（一定由类实现或有默认的构造函数）都会在本类的实现中给出，使用Dispatch函数能够将这三种情况都包含，简化代码。 

Virtual call 

receiver variable在例子中就是c。

对receiver c和c的所有直接间接子类都作为call site调用Dispatch 

CHA：Examples

• Resolve(c.foo()) = {C.foo()}：class C重新定义了foo()，所以c.foo()是一个普通私有函数调用，因此Resolve(c.foo()) = {C.foo()}
• Resolve(a.foo()) = {A.foo()，C.foo()，D.foo()}：a.foo()是一个virtual call，所以要对class A及其所有子类进行递归查找，因此Resolve(a.foo()) = {A.foo()，C.foo()，D.foo()}
• Resolve(b.foo()) = {A.foo()，C.foo()，D.foo()}：b.foo()是一个virtual call，所以要对class B及其所有子类进行递归查找，因此Resolve(a.foo()) = {A.foo()，C.foo()，D.foo()}

 

CHA in IDE (IntelliJ IDEA)

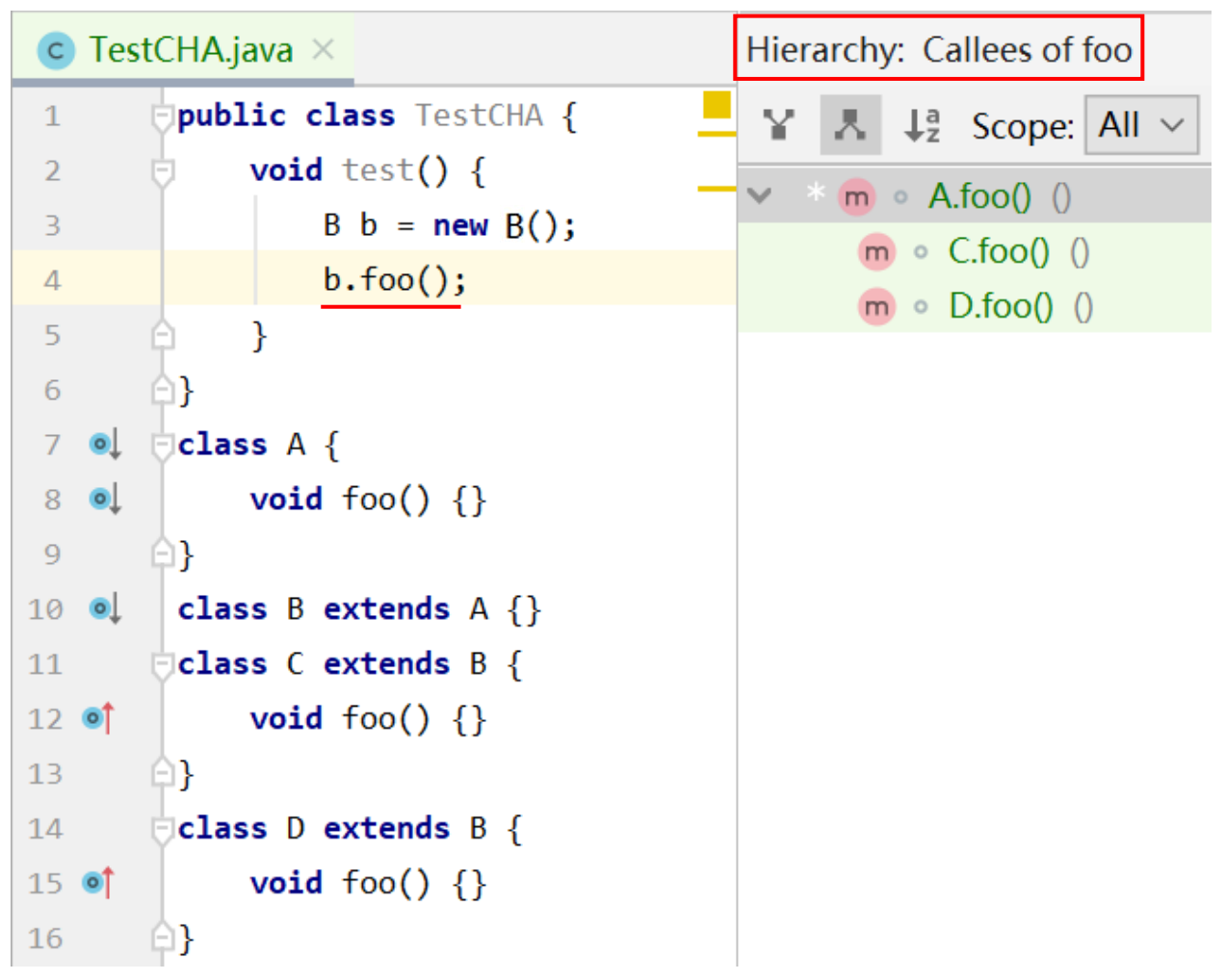
Features of CHA 

• Advantage: fast 
  • Only consider the declared type of receiver variable at the call-site, and its inheritance hierarchy
  • Ignore data- and control-flow information

• Disadvantage: imprecise
  • Easily introduce spurious target methods
  • Addressed in next lectures

Call Graph Construction: Algorithm

Idea

• Build call graph for whole program via CHA
  • 通过CHA构造整个程序的call graph
• Start from entry methods (focus on main method)
  • 通常从main函数开始
• For each reachable method 𝑚, resolve target methods for each call site 𝑐𝑠 in 𝑚 via CHA (Resolve(𝑐𝑠))
  • 递归地处理每个可达的方法
• Repeat until no new method is discovered
  • 当不能拓展新的可达方法时停止
  • 整个过程和计算理论中求闭包的过程很相似

Algorithm 

• Worklist：记录需要处理的methods
• Call graph：需要构建的目标，是call edges的集合
• Reachable method (RM)：已经处理过的目标，在Worklist中取新目标时，不需要再次处理已经在RM中的目标

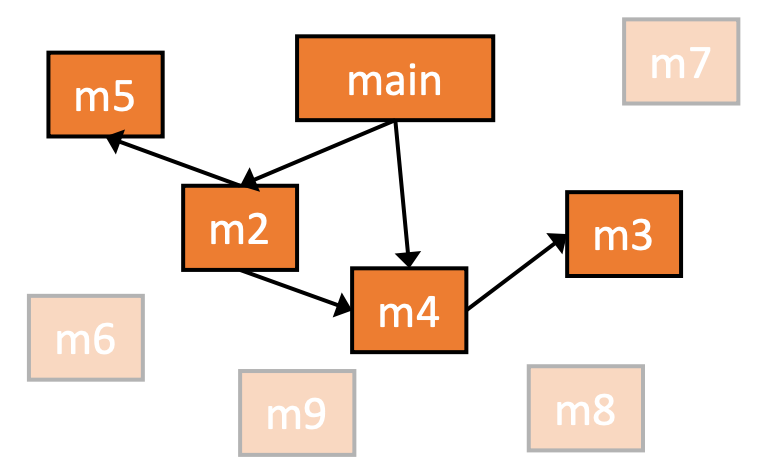
Example

1、初始化

2、处理main后向WL中加入A.foo()

3、继续分析，由于A.foo()之前已经处理过（在集合RM中），之后不会再进行处理

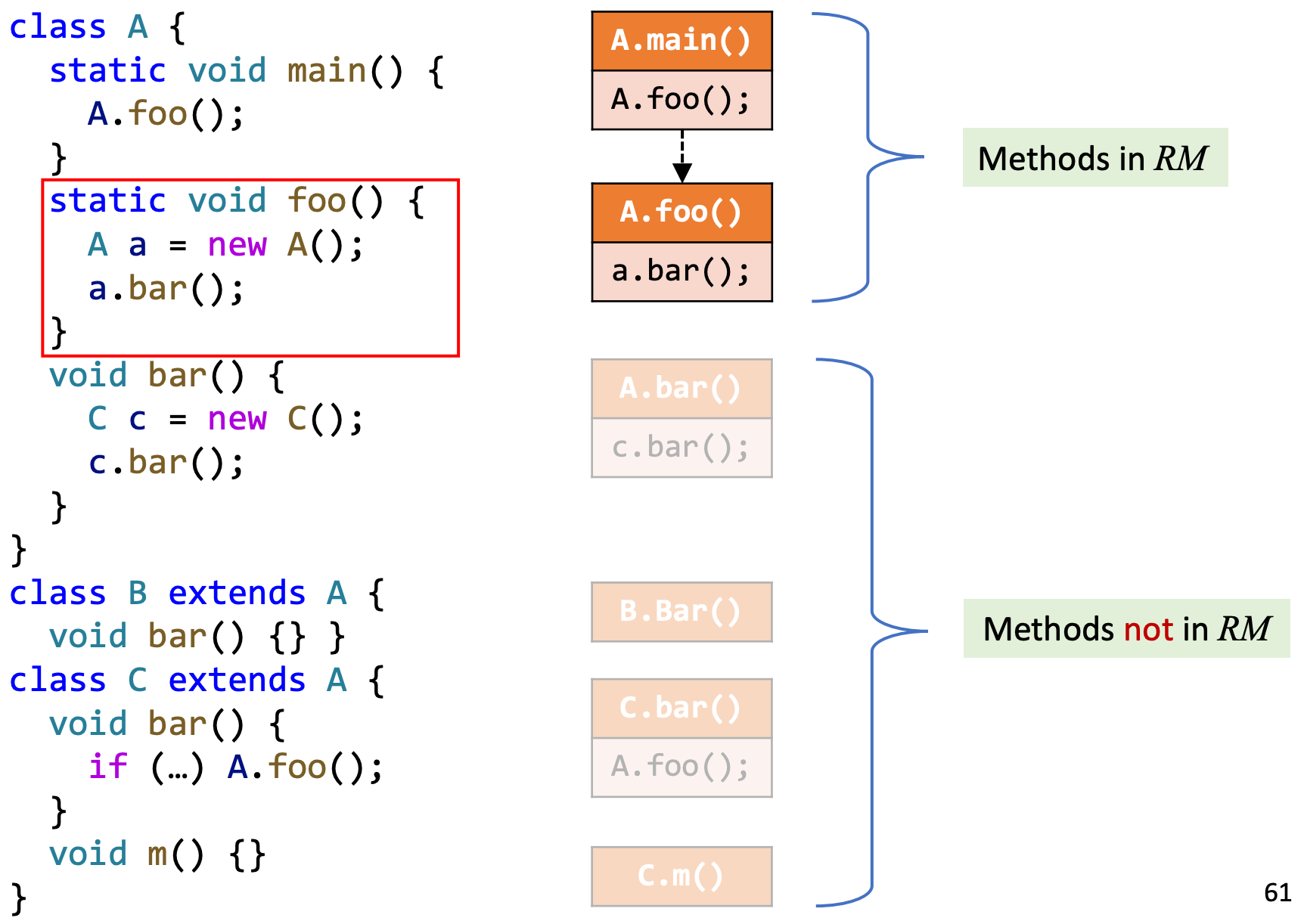
4、继续分析a.bar()，按照virtual call的规则进行may analyzes

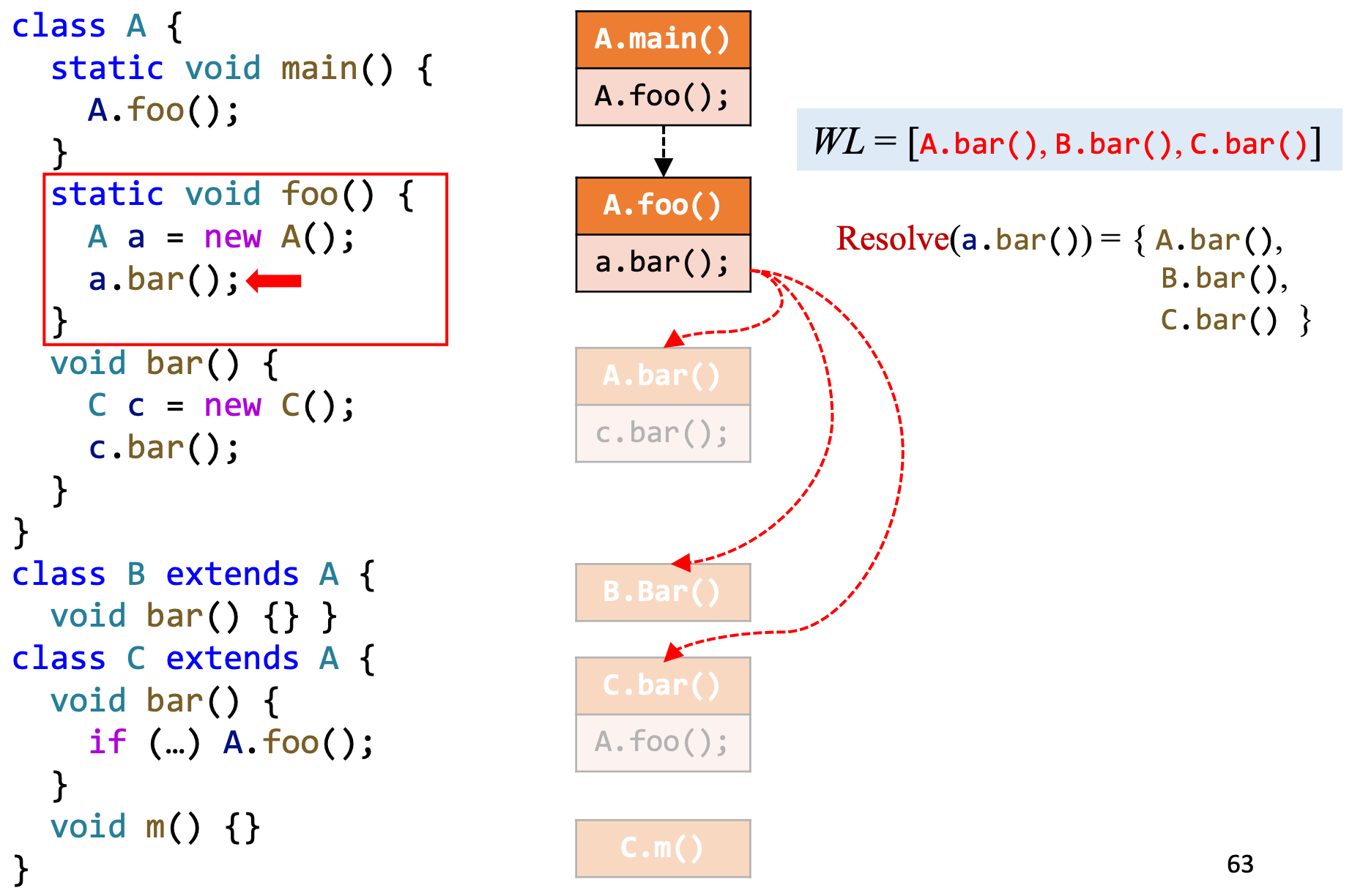
5、处理c.bar() 

6、处理B.bar()，因为B.bar()没有新的callsite，也没有继承子类，跳过

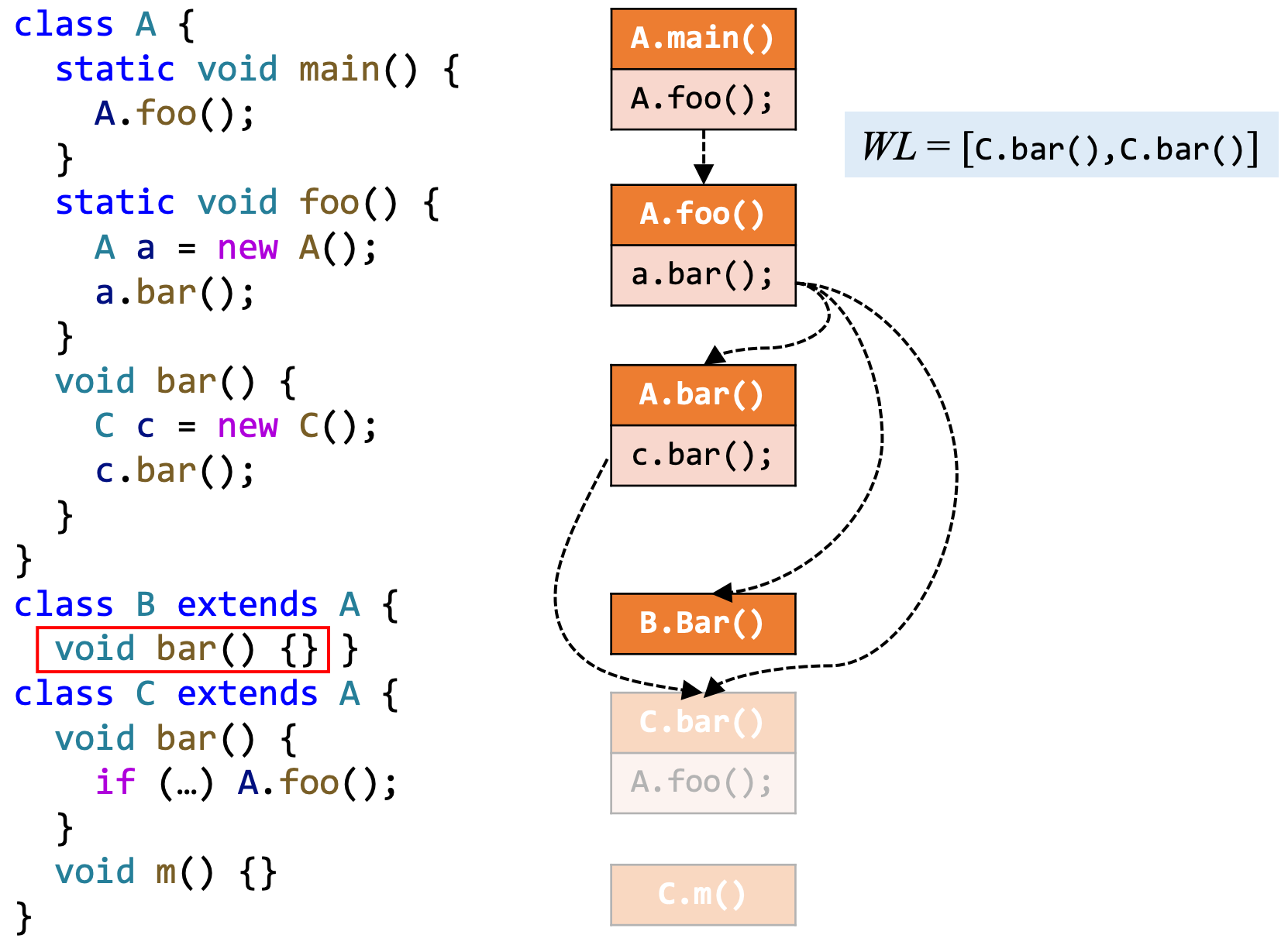
7、继续分析，由于A.foo()之前已经处理过（在集合RM中），之后不会再进行处理

8、C.m()是不可达的死代码 

 

三、Interprocedural Control-Flow Graph

• CFG represents structure of an individual method
• ICFG represents structure of the whole program，With ICFG, we can perform interprocedural analysis
• ICFG = CFGs + call & return edges
  • Call edges: from call sites to the entry nodes of their callees
  • Return edges: from exit nodes of the callees to the statements following their call sites (i.e., return sites)

 

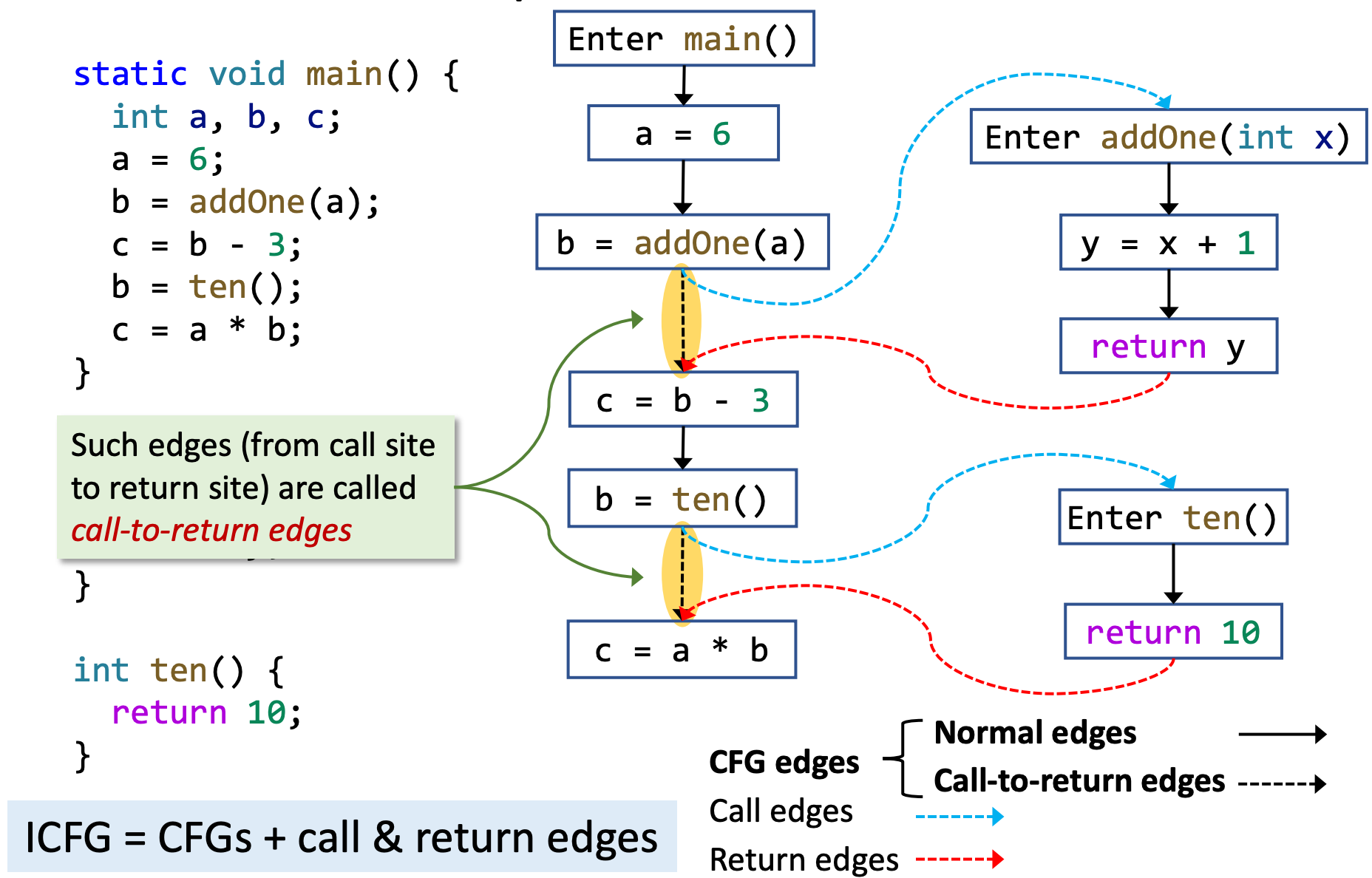
四、Interprocedural Data-Flow Analysis

Analyzing the whole program with method calls based on interprocedural control-flow graph (ICFG).

定义与比较

Edge transfer处理引入的call & return edge。为此，我们需要在CFG基础上增加三种transfer函数。 

• Call edge transfer：从调用者向被调用者传递参数
• Return edge transfer：被调用者向调用者传递返回值
• Node transfer：大部分与过程内的常数传播分析一样，不过对于每一个函数调用，都要kill掉LHS（Left hand side）的变量

下面以常量传播为例子进行解释。

• Node transfer
  • Call nodes: identity
  • Other nodes: same as intraprocedural constant propagation
• Edge transfer
  • Normal edges: identity
  • Call-to-return edges: kill the value of LHS variable of the
  • call site, propagate values of other local variables
  • Call edges: pass argument values
  • Return edges: pass return values

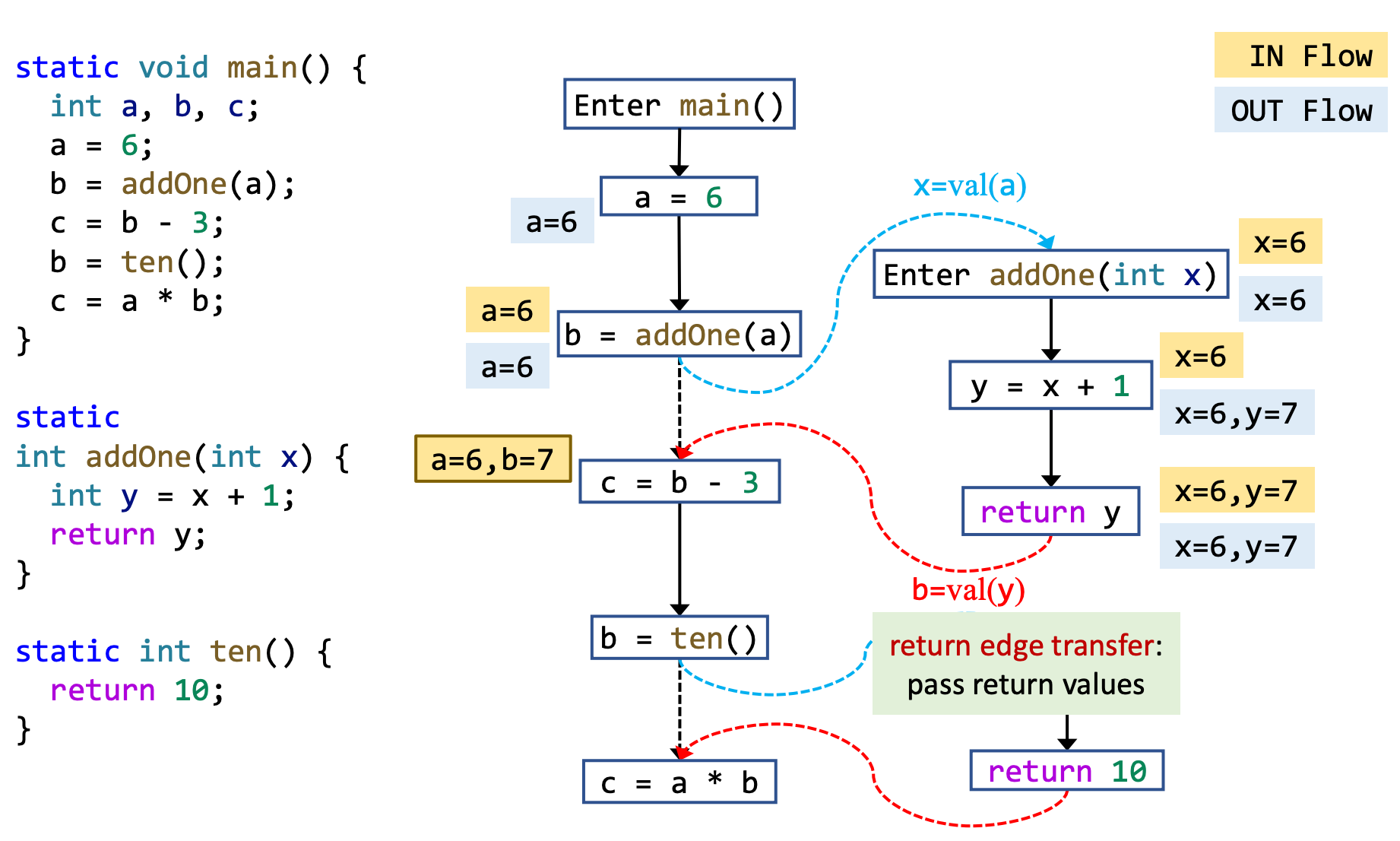
要记得在调用语句处kill掉表达式左边的值，否则会造成结果的不准确，如：

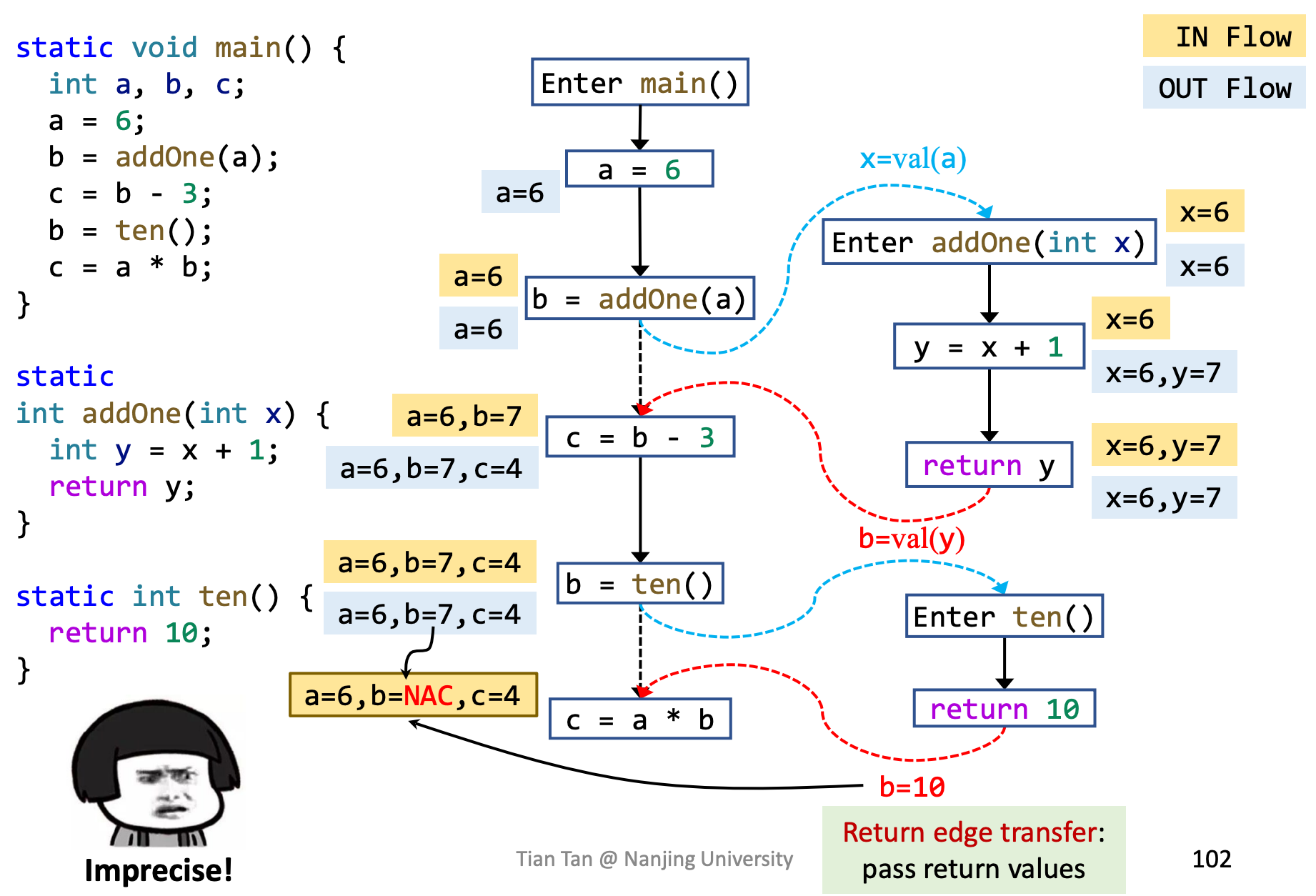
kill掉callsite b的左值后如下：

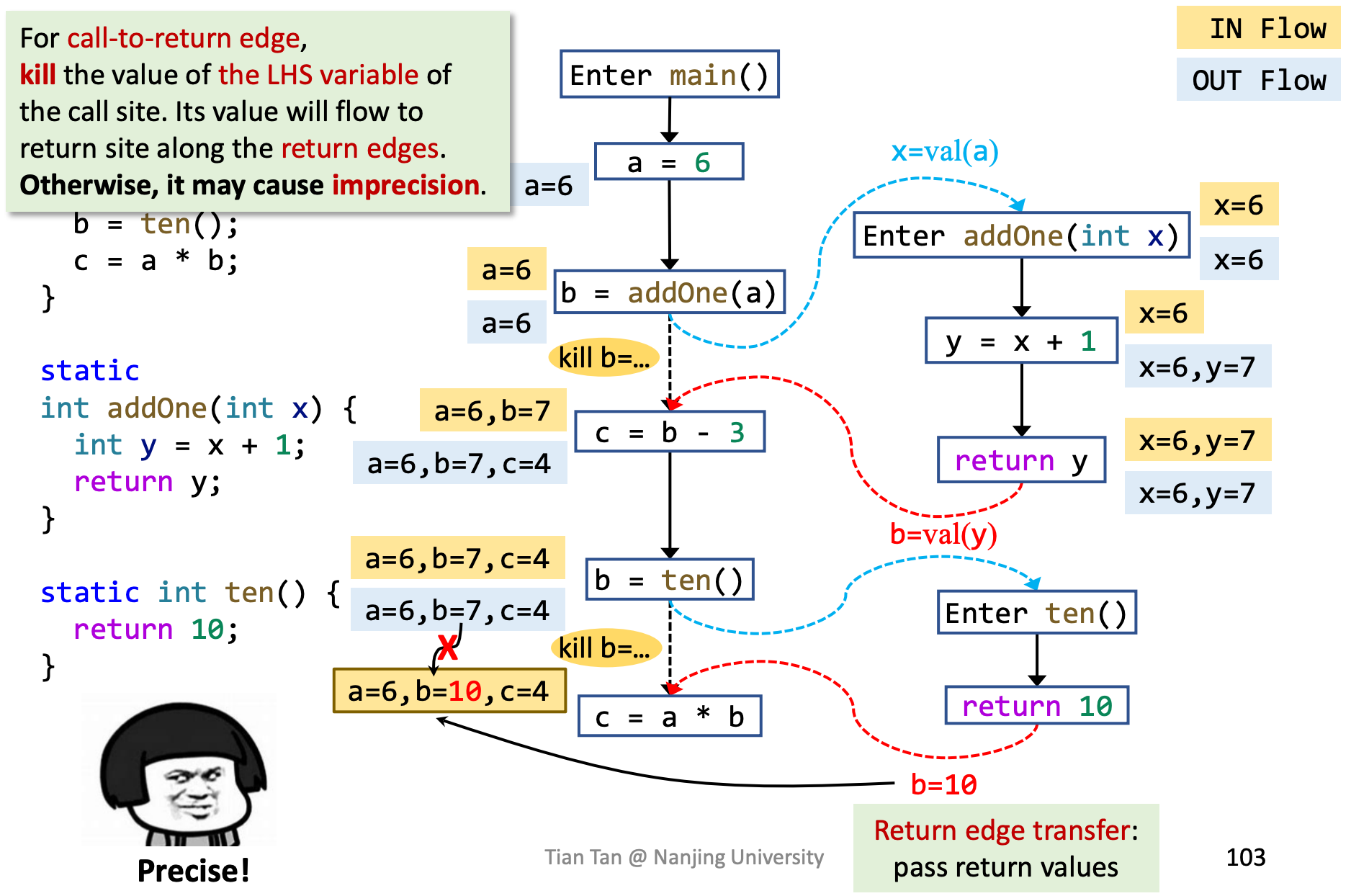
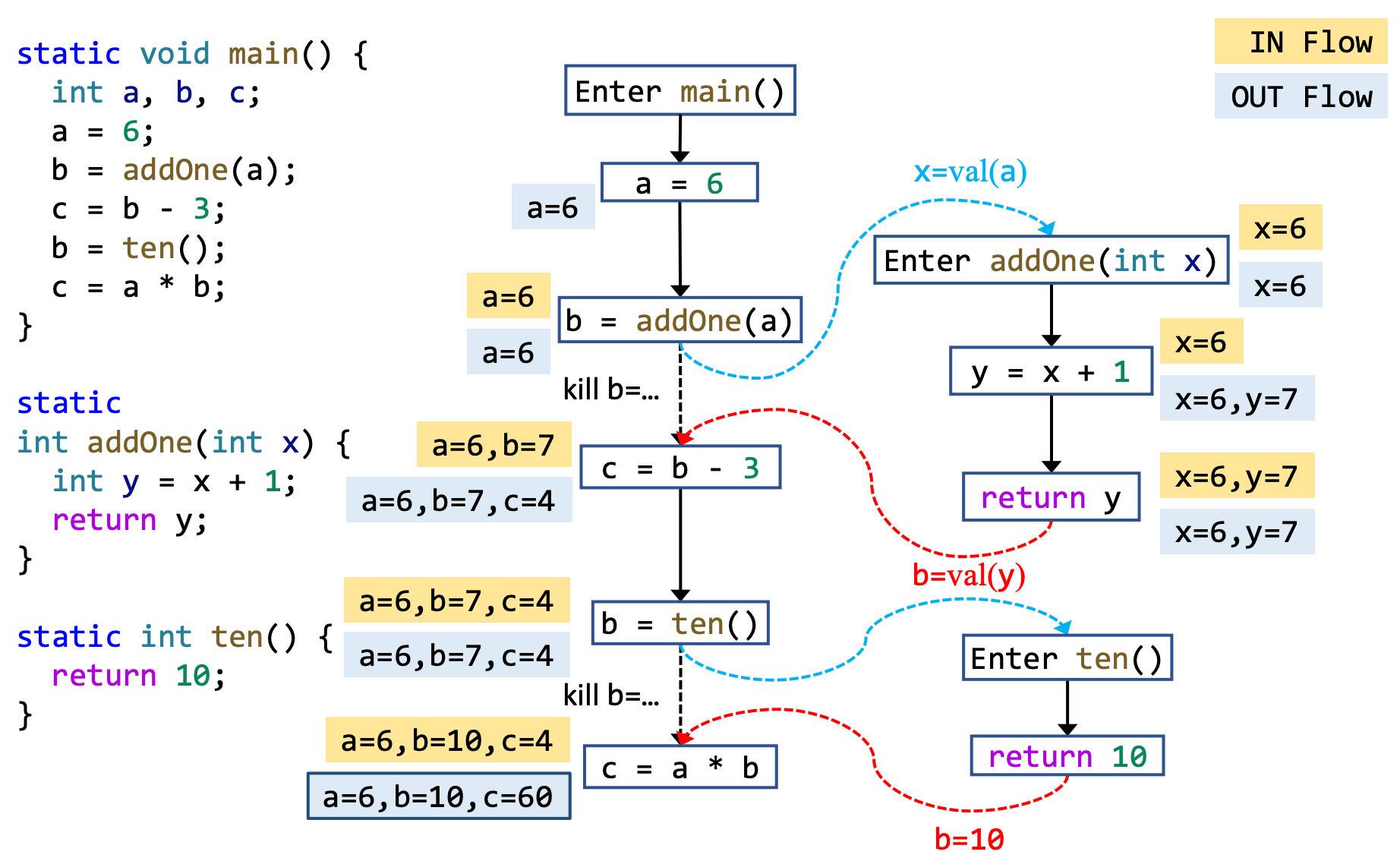
这里有一个问题要思考一下，这一段有存在的必要吗？

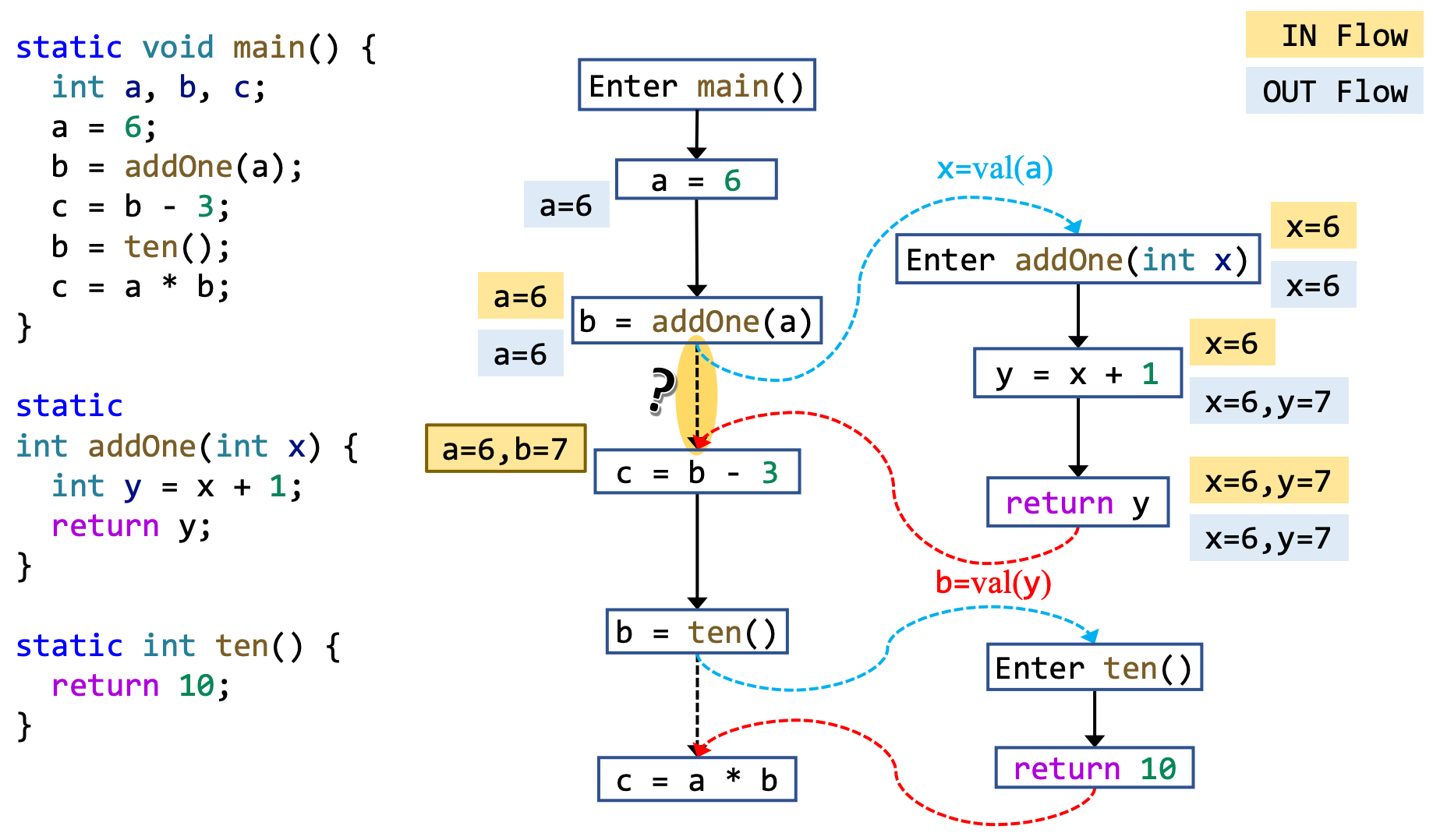
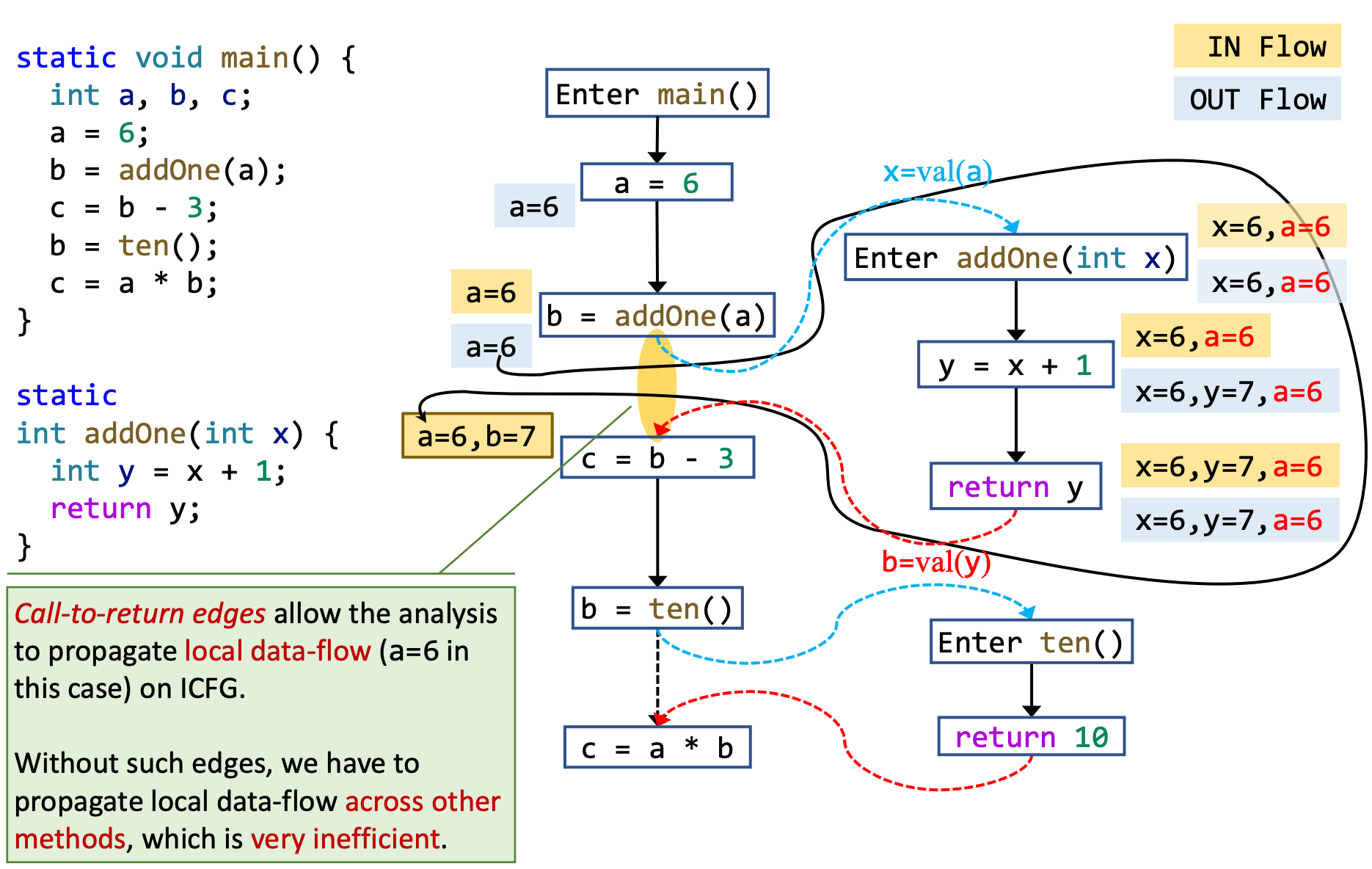
Such edge (from call site to return site) is named call-to-return edge. It allows the analysis to propagate local data-flow (a=6 in this case) on ICFG.

如果没有这一段，那么a就得“出国”去浪费地球资源——在分析被调用函数的全程中都需要记住a的值，这在程序运行时会浪费大量内存。

 

五、How Important Interprocedural Data-Flow Analysis

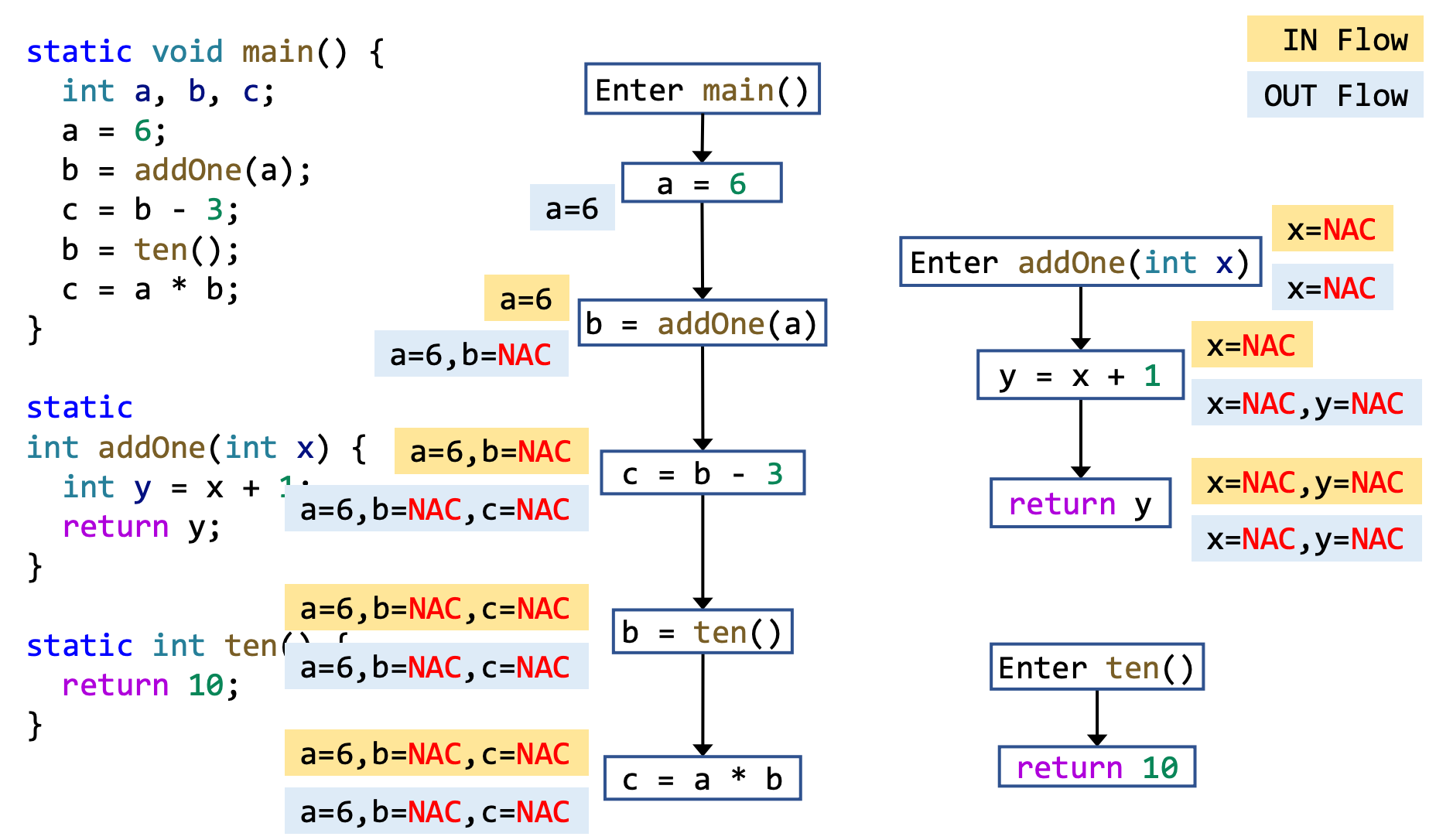
还是看上章的常量传播的例子， 而如果只做过程内分析，则精度大大下降：

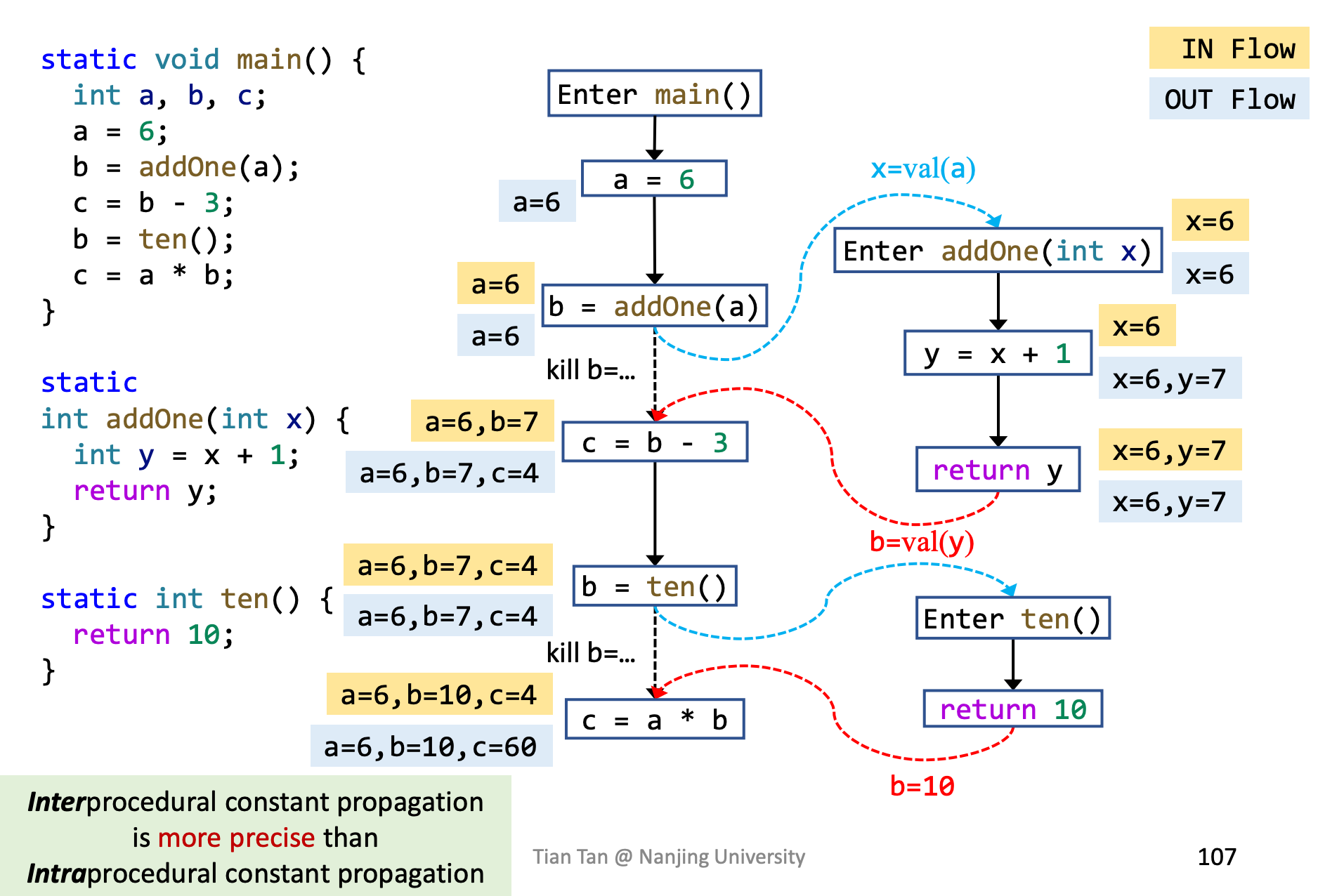
应用过程间分析的完整推导如下：