南京大学 静态软件分析(static program analyzes)-- Data Flow Analysis:Foundation 学习笔记
一、Iterative Algorithm, Another View
recall the iterative algorithm for data flow analysis
This general iterative algorithm produces a solution to data flow analysis.

给定一个有 k 个节点的 CFG,迭代算法会更新每个节点 n 的 OUT[n] 值。那么我就可以考虑把这些值定义为一个 k-tuple,每一个节点的值域空间设为V:
![]()
则,我们的数据流分析迭代算法框架就可记为:
![]() Vk代表着一个节点的k-tuple。
Vk代表着一个节点的k-tuple。
通过这个视角,整个data-flow analyzes迭代过程就可以重新表示为:

在这个框架下,我们就有一些想知道的问题:
- 算法是否确保一定能停止/达到不动点?会不会总是有一个解答?
- 如果能到达不动点,那么是不是只有一个不动点?如果有多个不动点,我们的结果是最优的吗?
- 什么时候我们会能得到不动点?
为了回答这个问题,我们需要先回顾一些数学。
二、Partial Order
所谓偏序集合(poset),就是一个由集合


- Reflexivity 自反性:x
x
- Antisymmetry 反对称性:x
y, y
x, 则 x = y
- Transitivity 传递性:x
y, y
z, 则 x
z
举几个例子:
- (S, ⊑) 是一个 poset,S 代表由整数构成的集合,⊑ 代表 ≤ (less than or equal to) 这种偏序关系。
- (S, ⊑) 不是一个 poset,S 代表由整数构成的集合,⊑ 代表 < (less than) 这种偏序关系。
- (S, ⊑) 是一个 poset,S 代表由英文单词构成的集合,⊑ 代表 子串(substring)这种偏序关系。
- (S, ⊑) 是一个 poset,S 代表集合 {a,b,c} 的幂集,⊑ 代表 ⊆(subset)这种偏序关系。
这里第三、第四个例子需要注意一下,
偏序关系与全序关系的区别在于,全序关系可以让任意两个元素比较,而偏序关系不保证所有元素都能进行比较。


三、Upper and Lower Bounds
给定一个偏序集
- 若存在集合u(u∈P),使得 S 的任意元素 x 都满足:x ⊑ u,则我们说 u 是 S 的上界(Upper bound)
- 若存在集合l(l∈P),使得 S 的任意元素 x 都满足:l ⊑ x,则我们说 l 是 S 的下界(Lower bound)
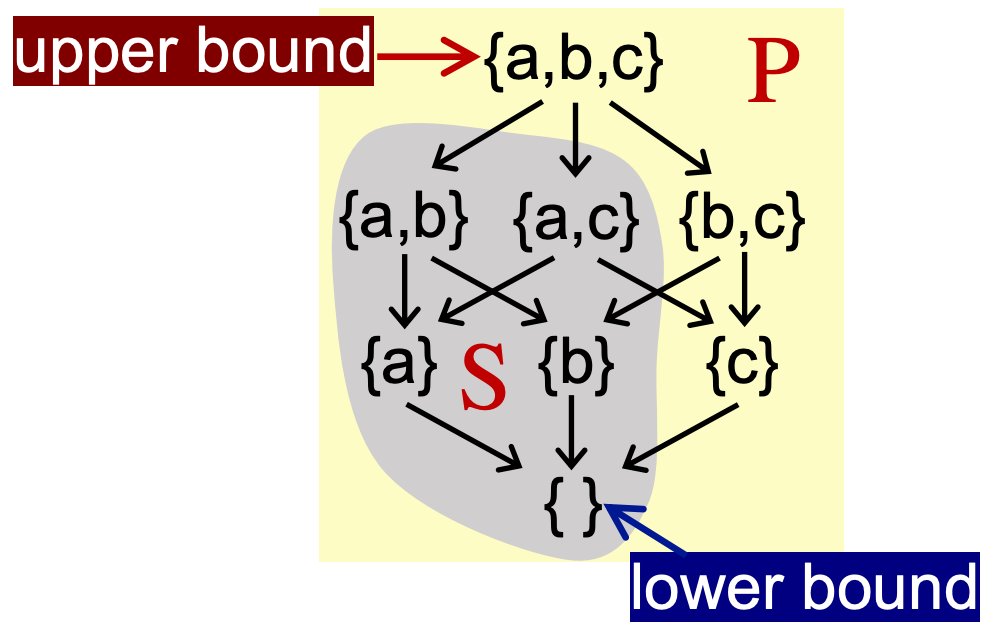
然后我们衍生出集合S的最小上界和最大下界的概念:
- 在 S 的所有上界中,我们记最小上界(Least upper bound,lub or join)为⊔S,满足所有上界 u 对 lub 有: ⊔S ⊑ u
- 在 S 的所有下界中,我们记最大下界(Greatest lower bound,glb, or meet)为⊓S,满足所有下界 l 对 glb 有: l ⊑ ⊓S
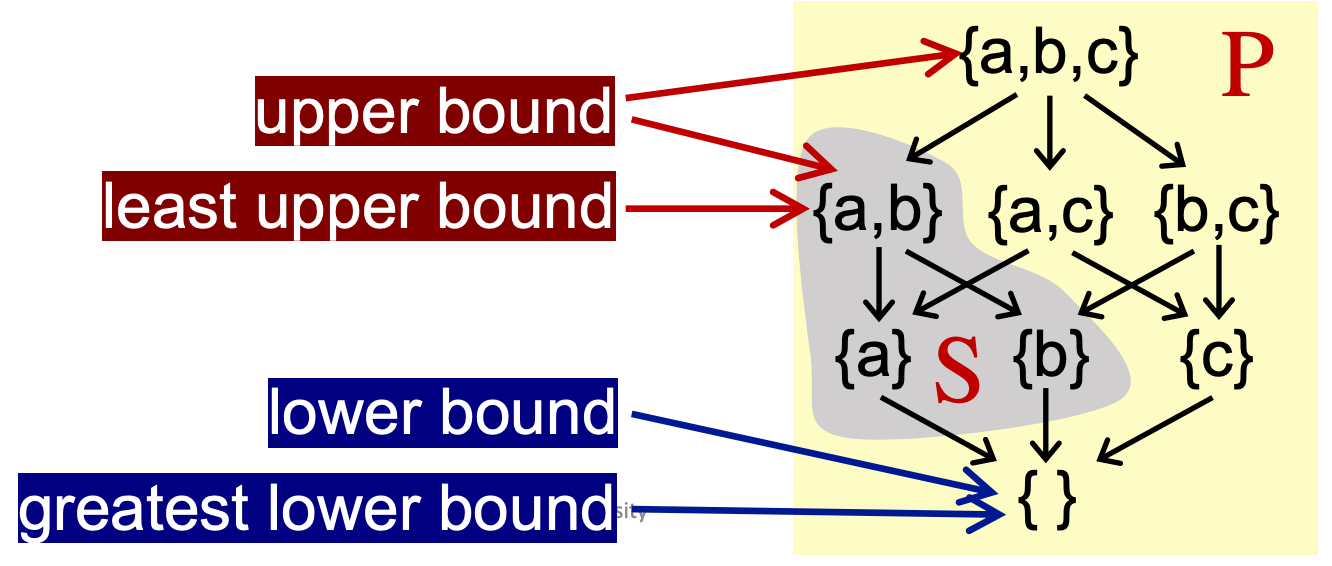
当 S 的元素个数只有两个{a, b}时,我们还可以有另一种记法:
- 最小上界⊔S:a ⊔ b (the join of a and b)
- 最大下界⊓S:a ⊓ b (the meet of a and b)
需要注意的是,并不是每个偏序集都有 lub 和 glb,但是如果有,那么该 lub, glb 将是唯一的。
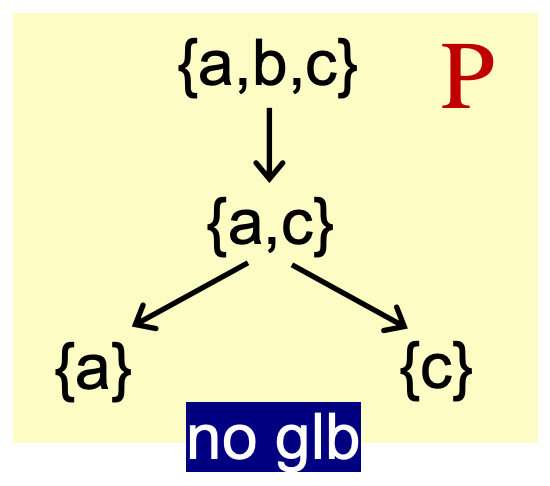
四、Lattice, Semilattice, Complete and Product Lattice
Lattice定义
给定一个偏序集

下面举几个例子:
- (S, ⊑) 是一个 lattice,S 代表由整数构成的集合,⊑ 代表 ≤ (less than or equal to) 这种偏序关系。
- (S, ⊑) 不是一个 lattice,S 代表由英文单词构成的集合,⊑ 代表 子串(substring)这种偏序关系。
- (S, ⊑) 是一个 lattice,S 代表集合 {a,b,c} 的幂集,⊑ 代表 ⊆(subset)这种偏序关系。
Semilattice定义
给定一个偏序集
- 如果只有 a ⊔ b 存在,那么偏序集
就叫做 join semilattice
- 如果只有 a ⊓ b 存在,那么偏序集
就叫做 meet semilattice
Complete Lattice
给定一个偏序集

下面举几个例子:
- (S, ⊑) 不是一个 complete lattice,S 代表由整数构成的集合,⊑ 代表 ≤ (less than or equal to) 这种偏序关系。
- (S, ⊑) 是一个 complete lattice,S 代表集合 {a,b,c} 的幂集,⊑ 代表 ⊆(subset)这种偏序关系。 ‘
- a greatest element T = ⊔P called top
- a least element ⊥ = ⊓P called bottom

Product Lattice
Given lattices L1 = (P1, ⊑1), L2 = (P2, ⊑2), …, Ln = (Pn, ⊑n), if for all i,(Pi, ⊑i) has ⊔i (least upper bound) and ⊓i (greatest lower bound), then we can have a product lattice Ln = (P, ⊑) that is defined by:
- P = P1 × … × Pn
- (x1, …, xn) ⊑ (y1, …, yn) ⟺ (x1 ⊑ y1) ∧ … ∧ (xn ⊑ yn)
- (x1, …, xn) ⊔ (y1, …, yn) = (x1 ⊔1 y1, …, xn ⊔n yn)
- (x1, …, xn) ⊓ (y1, …, yn) = (x1 ⊓1 y1, …, xn ⊓n yn)
即多个 lattice 的笛卡尔积也能形成一个新的 lattice,同时如果 product lattice L是全格的积,那么 L 也是全格。
五、Data Flow Analysis Framework via Lattice
从抽象视角来看,一个数据流分析框架(D, L, F)由以下元素组成:
- D:数据流的方向,前向还是后向
- L:包含了数据值域 V,和 meet, join 符号的格
- F:V -> V 的转移方程族

六、Monotonicity and Fixed Point Theorem
Monotonicity单调性
定义:A function f:L → L (L is a lattice) is monotonic if ∀x, y ∈ L, x ⊑ y ⟹ f(x) ⊑ f(y).
Fixed-Point Theorem不定点定理
给定一个全格,(L, ⊑),如果满足:
- f: L → L is monotonic
- L is finite
那么:
- the least fixed point of f can be found by iterating f(⊥), f(f(⊥)), …, fk(⊥) until a fixed point is reached
- the greatest fixed point of f can be found by iterating f(T), f(f(T)), …, fk(T) until a fixed point is reached
证明过程(Existence of Fixed Point):

证明过程(Least Fixed Point):

同理证明过程(Greast Fixed Point)
通过上面的证明,我们又回答了一个问题:如果我们的迭代算法符合不动点定理的要求,那么迭代得到的不动点,确实就是最优不动点(即唯一最优解)。
七、Relate Iterative Algorithm to Fixed Point Theorem
首先定义抽象:
- 对此时的lattice的定义:迭代算法的元素为各状态的product,是有限全格
- 对此时的f的定义:迭代算法的操作则可以看做是对格点依次应用转换规则f1(L -> L),以及对控制流应用meet/join function(⊔/⊓: L x L -> L )

根据不动点定理的定义,迭代算法需要满足该定义(有限lattice,f单调)的证明。迭代算法的元素为各状态的product,是有限全格。接下来我们证明转换规则f的单调性。
我们的迭代函数 F 包括了转移函数 f 和 join/meet 函数,证明 F 是单调的,那么也就能得到 F: L -> L 是单调的。

于是我们就完成了迭代算法到不动点定理的对应。
现在我们可以来回答迭代算法的停机问题,即什么时候算法停机?即这个算法最大的步数是多少?
要回答这个问题,需要引入“height of a lattice h”的概念,每个 lattice 都有其高度。假设 lattice 的高度为 h,h 代表了 lattice 中最常路径的长度。

我们的 CFG 节点数为 k,就算每次迭代只能使一个节点在 lattice 上升一个高度,那么最坏情况下,我们的迭代次数也就是 i = h^k
最后我们再列出这三个问题与其回答:
- 算法是否确保一定能停止/达到不动点?如果能!会不会总是有一个解答?可以!
- 如果能到达不动点,那么是不是只有一个不动点?如果可以有很多。如果有多个不动点,我们的结果是最优的吗?是的!
- 什么时候我们会能得到不动点?最坏情况下,是 lattice 的高度与 CFG 的节点数的乘积。
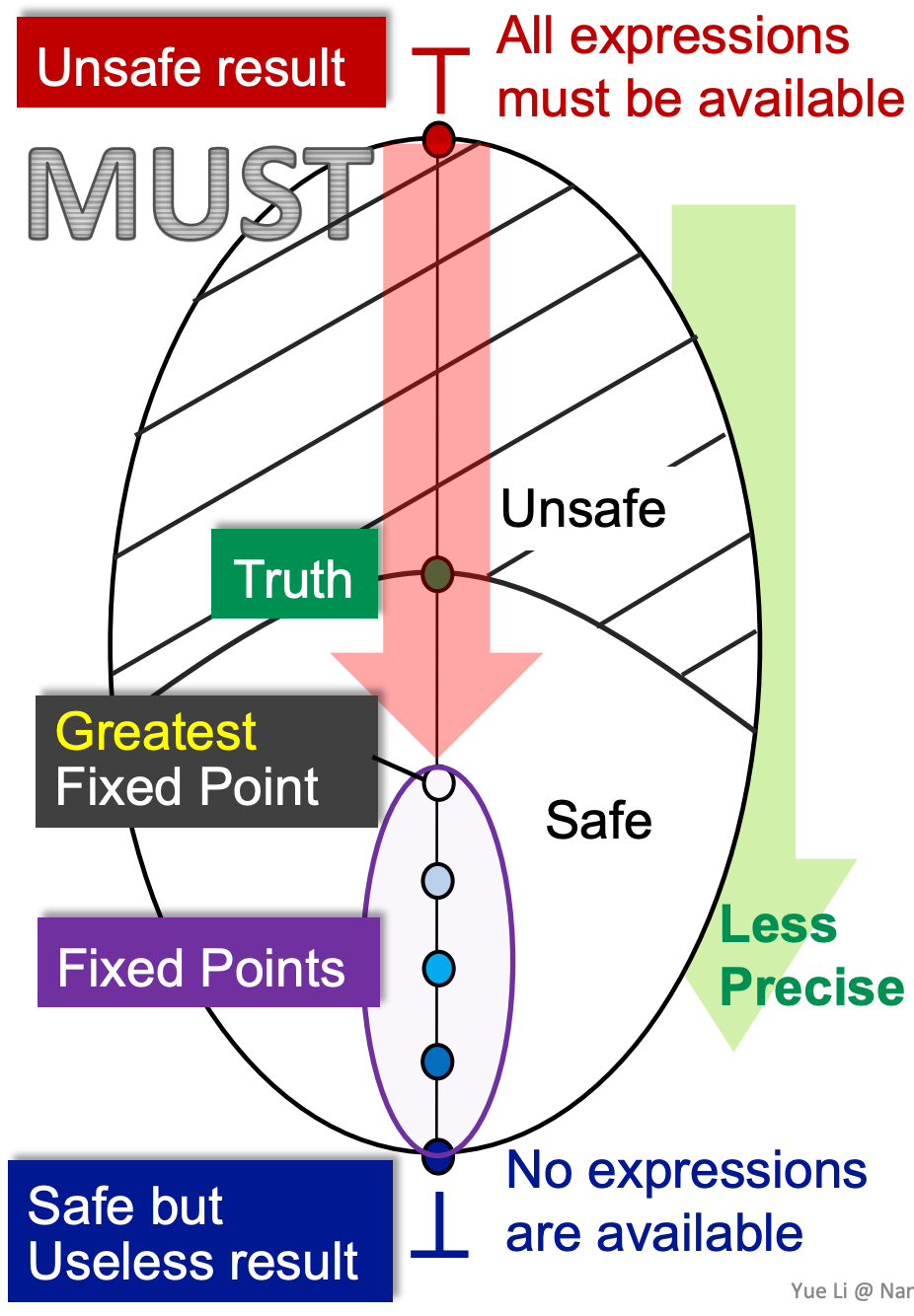
八、May/Must Analysis, A Lattice View
无论 may 还是 must 分析,都是从一个方向到另一个方向去走。考虑我们的 lattice 抽象成这样一个视图:
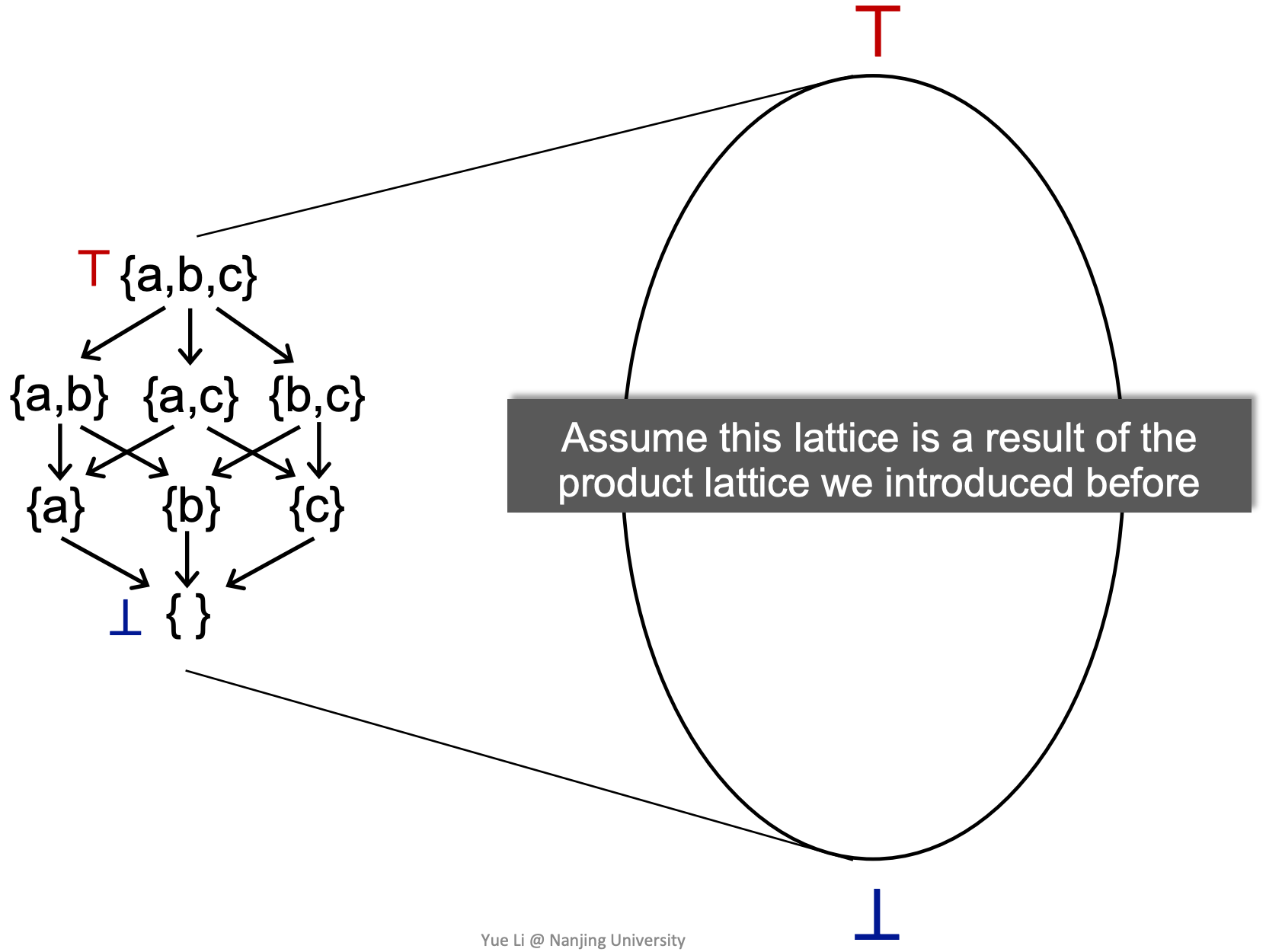
以Reaching Definitions Analyzes为例
- 下界代表没有任何可到达的定值
- 上界代表所有定值都可到达
我们知道,静态分析的抽象Abstraction是和具体的任务目标语境有关的,
- 下界代表 unsafe 的情形,即我们认为任何定值都无法到达。可对相关变量的存储空间进行替换 or 该文件不存在潜在污点流传播风险,这是一种complete but not sound的结果。在这里,complete but not sound就意味着unsafe,因为可能漏报
- 上界代表 safe but useless 的情绪,即认为定值必然到达。所有相关变量都不可替换 or 所有文件被被判定为存在污点流传播风险,这相当于一棒子把所有人都打死,是一种sound but not complete的结果,这里sound but not complete就意味着safe but useless,因为可能产生大量误报
而因为我们采用了 join 函数,那么我们必然会从 lattice 的最小下界往上走。而越往上走,我们就会失去更多的精确值。那么,在所有不动点中我们寻找最小不动点,那么就能得到了在保证safe的前提下精确值最大的不动点结果。

以Available Expressions Analyzes为例
- 下界代表无可用表达式
- 上界代表所有表达式都可用
结合可用表达式分析的具体任务目标语境,我们有,
- 下界代表 safe but useless 的情形,因为需要重新计算每个表达式,即使确实有表达式可用。这会导致大量的漏报
- 上界代表 unsafe,因为不是所有路径都能使表达式都可用。这会导致误报
与 may analysis 一样,通过寻找最大不动点,我们能得到safe的结果中精确值最大的结果。
9. MOP and Distributivity
Meet-Over-All-Paths Solution (MOP)
我们引入 Meet-Over-All-Paths Solution,即 MOP。在这个 solution 中,我们不是根据节点与其前驱/后继节点的关系来迭代计算数据流,而是直接查找所有路径,根据所有路径的计算结果再取上/下界。
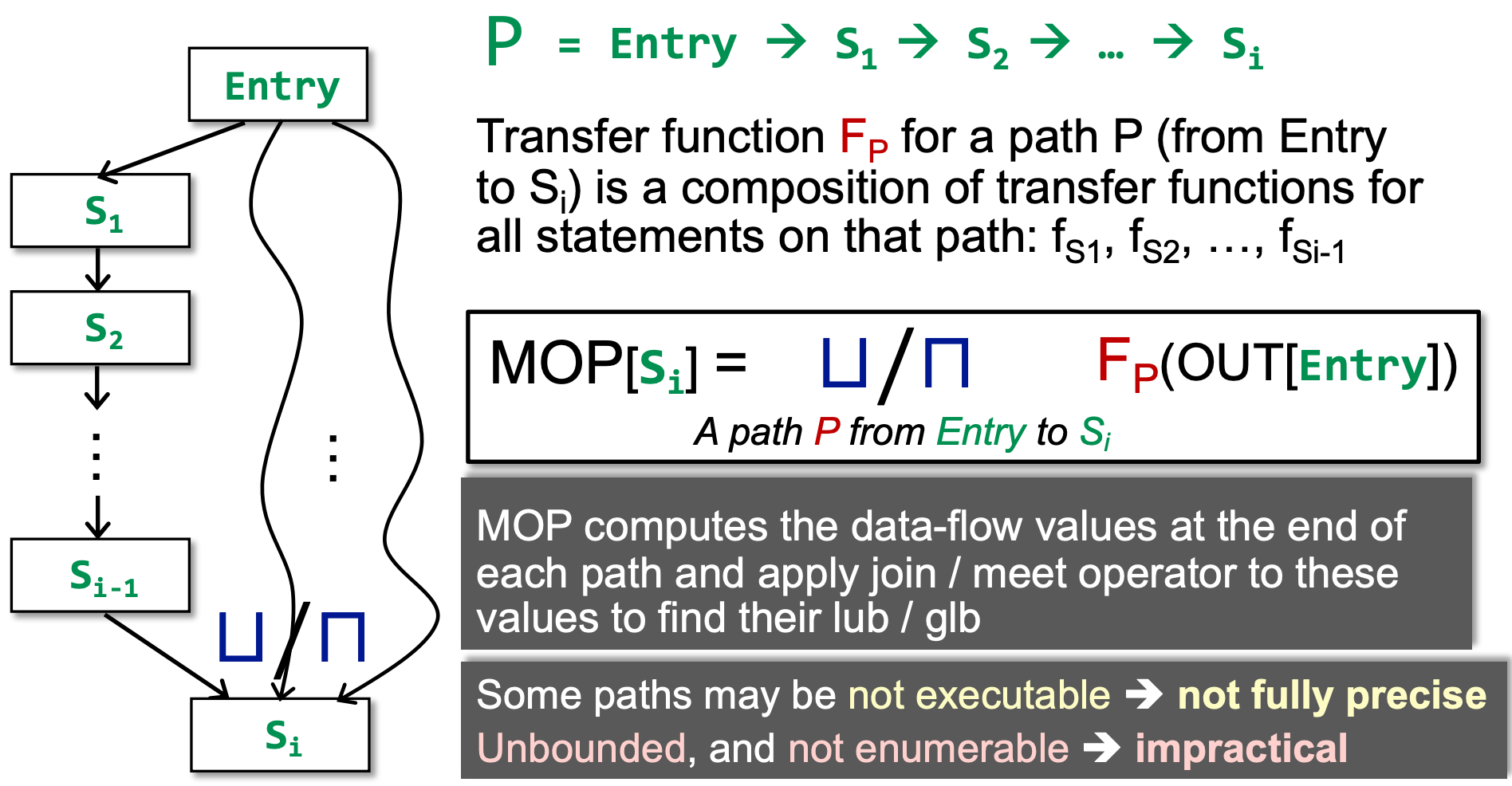
Ours (Iterative Algorithm) vs. MOP

可以看到,
- 迭代算法是 s3 对前驱取 join 后进行进行 f3 的转移
- MOP 算法是对到达 s3 之后,s4 之前的路径结果取 join
那么迭代算法和 MOP 哪个更精确呢?我们下面来证明一下。

以上证明表明 MOP 是更为精确的。
特别地,如果 F 是可分配的(满足分配率),那么确实可以让偏序符号改为等于号。

在之前的例子中(Reaching Definitions Analysis、Live Variables Analysis、Available Expressions Analysis),在 gen/kill problem 下,F 满足可分配。因此在前面的例子中,迭代算法的精度与 MOP 相等。
十、Constant Propagation
在另一些场景下,F 是不可分配的,如常量传播(Constant Propagation)。
常量传播定义:Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p.
- The OUT of each node in CFG, includes a set of pairs (x, v) where x is a variable and v is the value held by x after that node
我们来回顾一下data flow analysis framework (D, L, F)的定义:
- D:a direction of data flow:forwards or backwards
- L:a lattice including domain of the values V and a meet ⊓ or join ⊔ operator
- F:a family of transfer functions from V to V
Domain
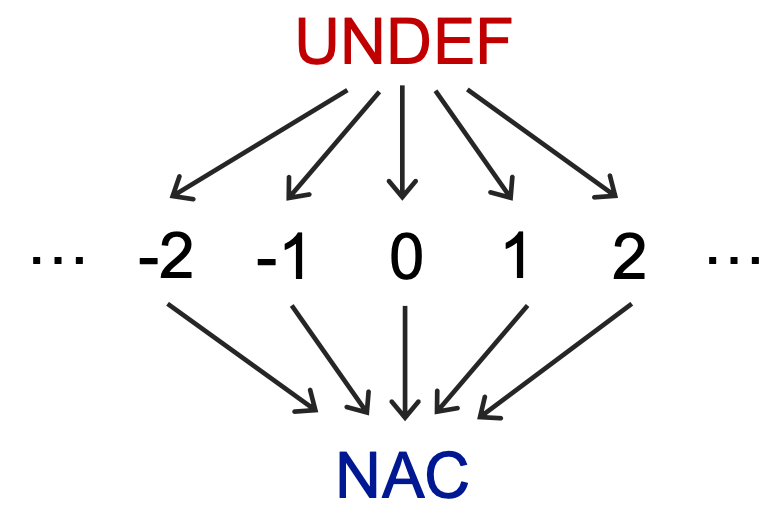
Lattice
在常量传播分析中,
- 最大上界是 undefine,因为我们不知道一个变量到底被定义为了什么值
- 最小下界是 NAC(Not A Constant),这是safe的
- 中间就是各种常量。这是因为分析一个变量指向的值是否为常量,那么要么它是同一个值,要么它不是常量

Transfer Function
给定一个 statement s: x = ...,我们定义转移函数:
![]()
其中我们根据赋值号右边的不同,决定不同的 gen 函数:

Nondistributivity
常量传播是不可分配的。以下图为例:
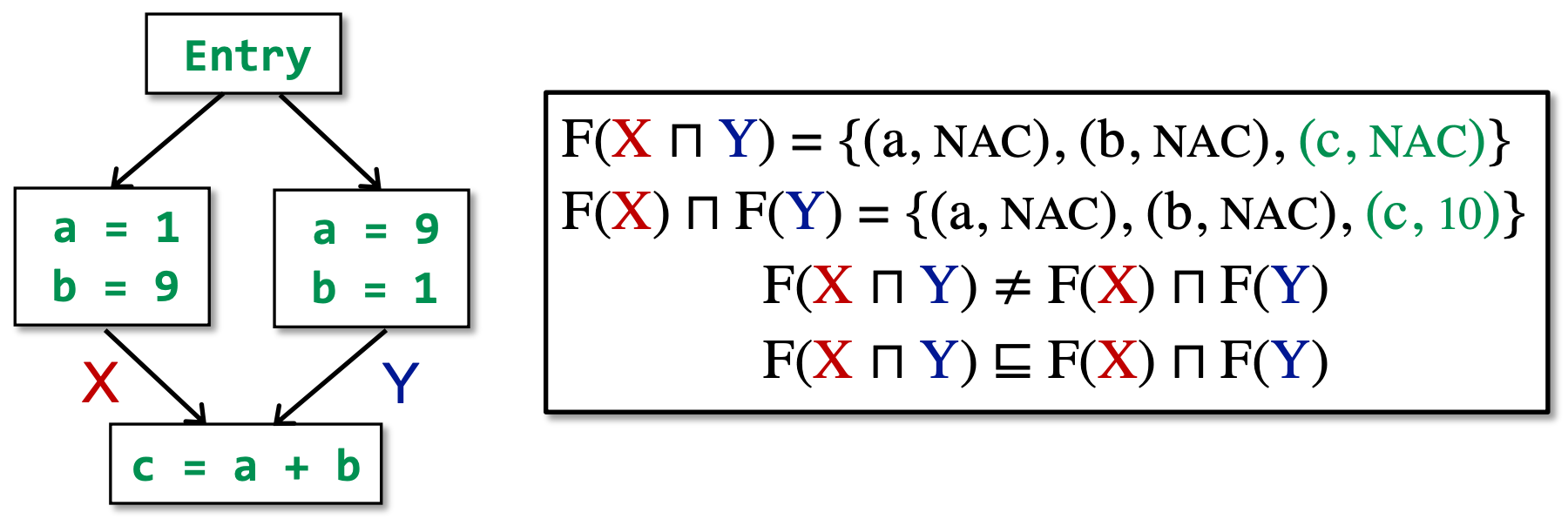
以上证明表明constant propagation analysis是单调的。
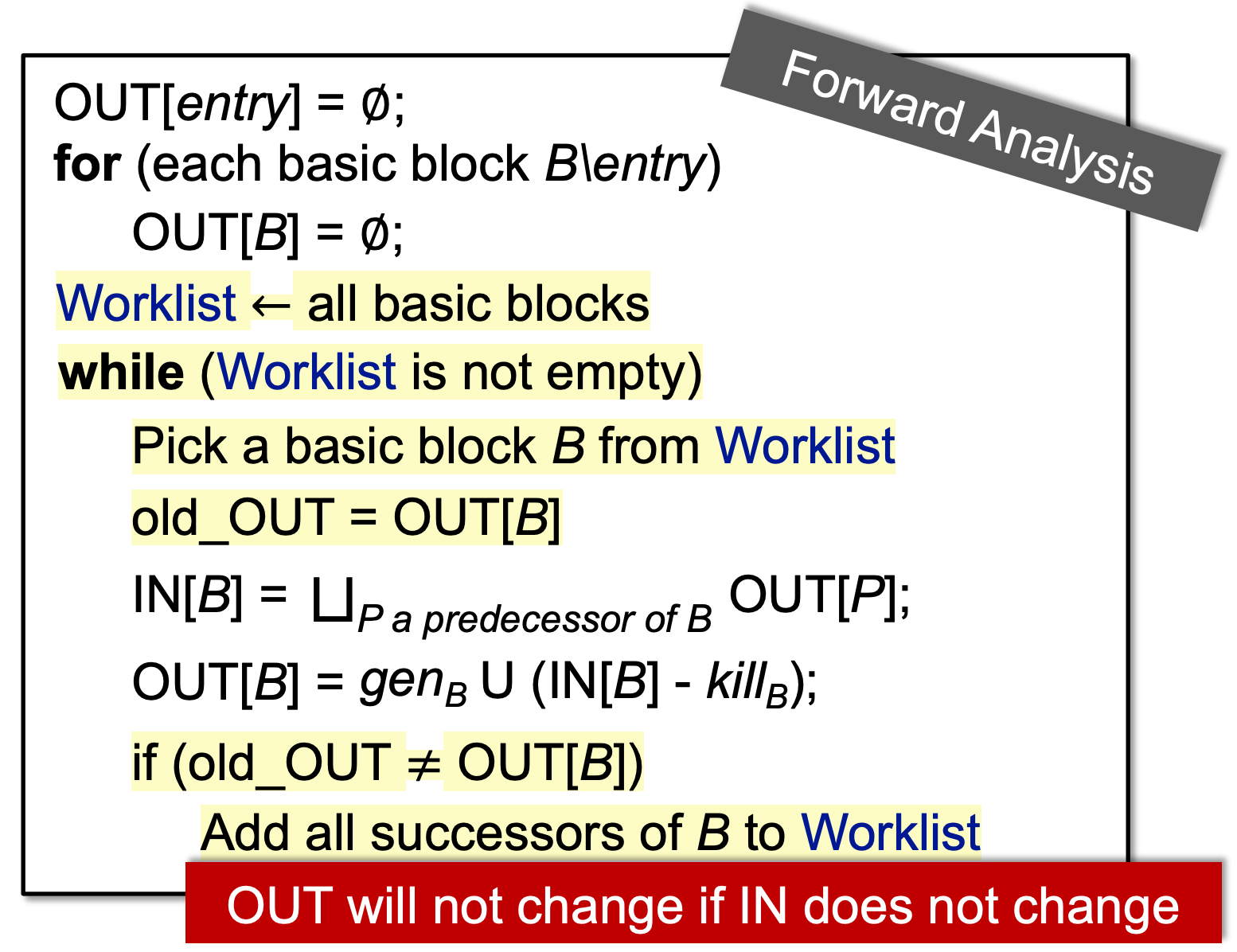
十一、Worklist Algorithm



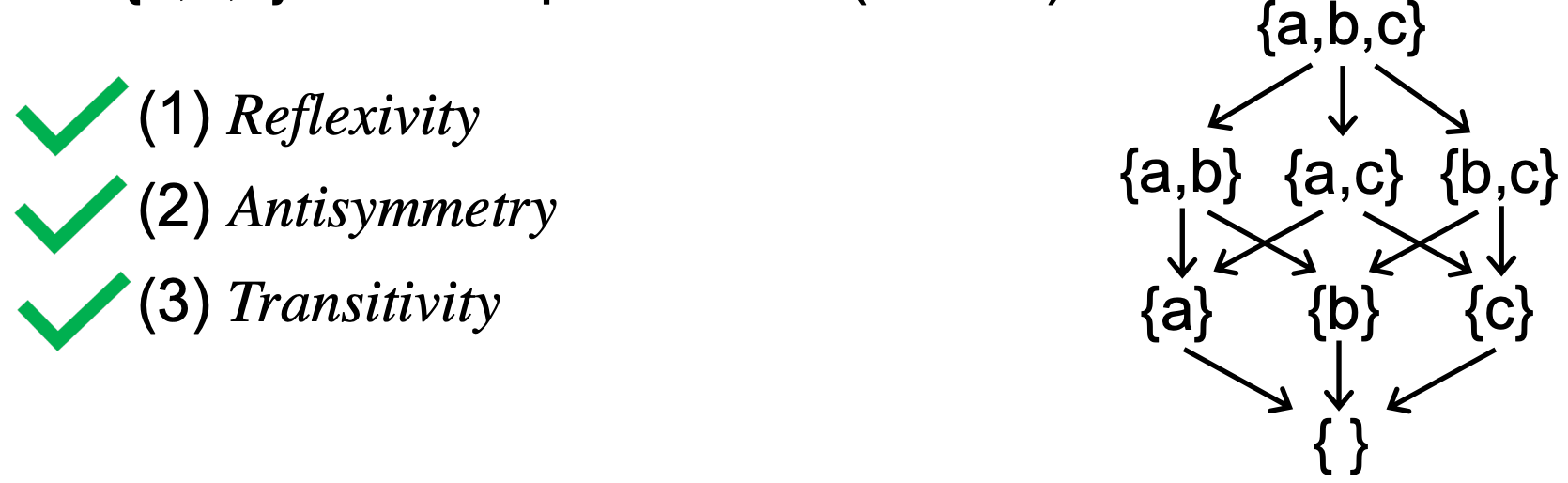


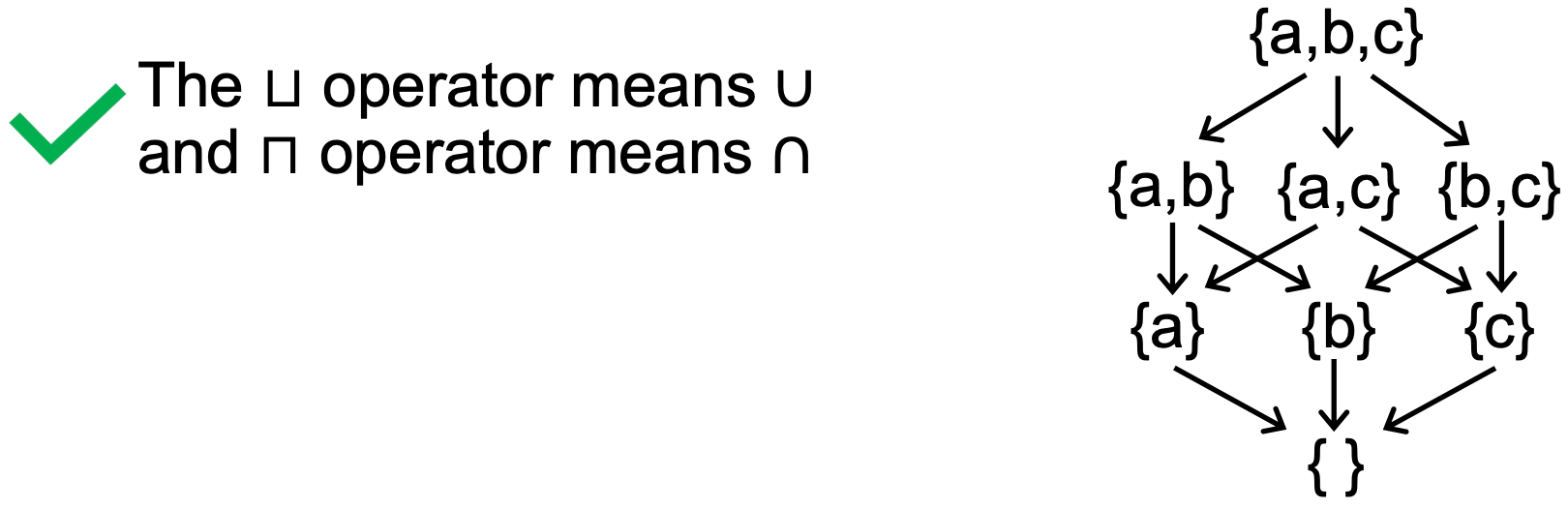



 浙公网安备 33010602011771号
浙公网安备 33010602011771号