树状数组

引入

已知一个数列，树状数组可以在 \(O(\log n)\) 的时间内维护以下操作：

将某一个数加上 \(x\)
求出某区间每一个数的和

lowbit 操作

\(lowbit(x)\) 指一个数 \(x\) 最低位 \(1\) 的位权。

负数的补码是其反码加一。如 \(-4=-(000\cdots0100)_2=(111\cdots1011)_2+1\)。\(x\) 的相反数会将其低位的 \(0\) 全部变成 \(1\)，再加 \(1\) 会把低位连续的 \(1\) 全部变成 \(0\)，同时进位。如：

\[\begin{array}1 原码 & 000\cdots01\color{red}{00}\\ 反码 & 111\cdots10\color{red}{11}\\ 补码 & 111\cdots1\color{red}{100} \end{array} \]

因此，\(x\&-x\) 的结果就是 \(x\) 最低位的 \(1\) 的位权，即 \(lowbit\)。

int lowbit(int x) { return x&-x; }

树状数组的结构

如果没有修改操作，区间和问题可以用前缀和在 \(O(1)\) 的时间内解决。

加上修改操作之后，单次修改需要 \(O(n)\) 的时间重新维护前缀和，难以承受。

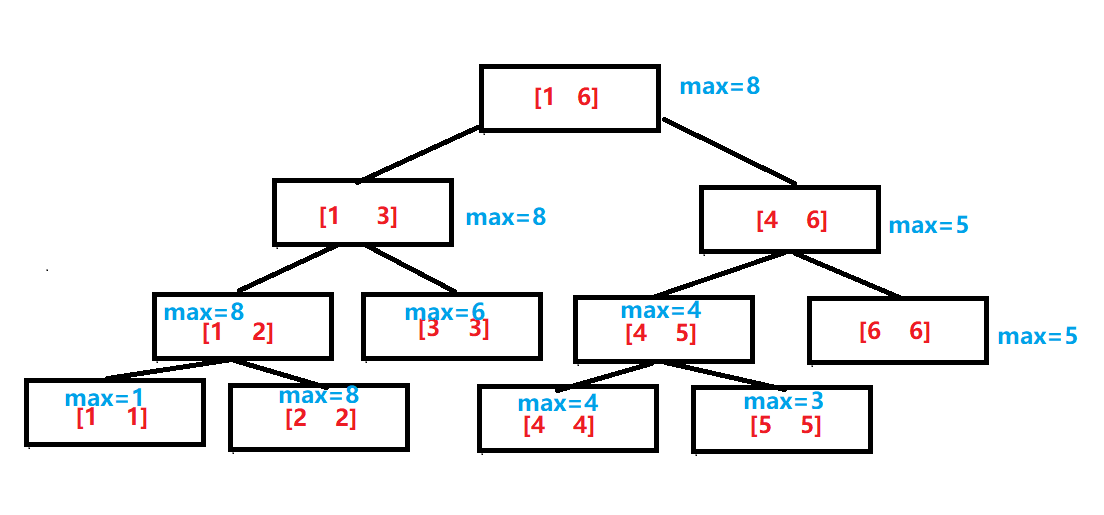
我们可以考虑将原数列拆分为若干段长度为 \(2^k\) 的块，每次修改只修改有限的块，每次查询将指定的块合并，以平衡修改和查询的时间复杂度。

^[1]

上图所示的这种数据结构称为线段树，而树状数组可以视为线段树的简化版本。树状数组的结构如下图所示：

^[2]

树状数组的结构具有以下三个特点：

从上往下看，树状数组相当于砍去了线段树的每一个右儿子
每一层从左往右看，节点呈间隔分布
下标为 \(i\) 的位置存放着区间 \([i-lowbit(i)+1,i]\) 的信息，该位置是其所在块的末端

我们从树状数组的结构出发理解其代码。

考虑查询操作。记当前所在位置为 \(x\)，\(x\) 存储着 \([x-lowbit(x)+1,x]\) 的信息，而这个区间的前一个区间应该以 \(x-lowbit(x)\) 结尾。在进行查询操作时我们可以直接跳到 \(x-lowbit(x)\)，从结果上看，查询的过程相当于对 \(x\) 做二进制拆分，当 \(x=0\) 时查询结束。

for (; x <= n; x += lowbit(x)) { t[x] += d; }

考虑修改操作。记当前所在位置为 \(x\)，我们需要找到所有包含 \(x\) 的区间并进行修改。从结构上看，\([x-lowbit(x)+1,x]\) 这个区间所在一层的上一层就是下一个需要修改的区间，而根据每一层节点间隔分布的性质，\(x\) 右侧被砍去了一个长度为 \(lowbit(x)\) 的区间，而 \(x+lowbit(x)\) 是这个区间的结尾，也是上一层父区间的结尾。因此，从结果上看，修改的过程相当于不断对 \(x\) 累加 \(lowbit(x)\)。

for (; x; x -= lowbit(x)) { res += t[x]; }

需要特别注意的是，树状数组是利用下标的二进制工作的，其结构要求了下标必须从 \(1\) 开始，尝试修改/询问 \(0\) 都会爆炸。

基本操作及模板

树状数组的基本操作分为三类：

①单点修改+区间查询，详见【模板】树状数组 1；
②区间修改+单点查询，详见【模板】树状数组 2；
③区间修改+区间查询，详见 243. 一个简单的整数问题2。

第一种操作是树状数组的模板，核心代码如下：

int n, t[N];
int lowbit(int x) { return x&-x; }
void modify(int x, int d)
{
	for (; x <= n; x += lowbit(x)) {
		t[x] += d;
	}
}
int query(int x)
{
	int res = 0;
	for (; x; x -= lowbit(x)) { res += t[x]; }
	return res;
}

使用树状数组维护差分，可以将第二类操作转换为第一类操作。

if (op == 1) {
    int x, y, k; cin >> x >> y >> k;
    modify(x, k);
    modify(y+1, -k);
} else {
    int x; cin >> x;
    cout << a[x] + query(x) << endl;
}

而第三种操作一般采用线段树实现，树状数组解法详见例题。

除此之外，树状数组还可以用于解决带修前缀最值问题（后文有提及）。在做题时，一种便捷的思路是将题意转化为三种基本操作中的一种，如单点修改+区间查询，然后直接套用树状数组。

243. 一个简单的整数问题2

用树状数组维护区间修改+区间查询的操作。

记 \(a\) 的差分数组为 \(d\)，\(a_i=\displaystyle\sum_{j=1}^id_j\)，把前缀和转化为对差分数组求和：

\[\begin{array}l d_1 & d_2 & d_3 & \cdots & d_n\\ \color{red}{d_1} & d_2 & d_3 & \cdots & d_n\\ \color{red}{d_1} & \color{red}{d_2} & d_3 & \cdots & d_n\\ \cdots\\ \color{red}{d_1} & \color{red}{d_2} & \color{red}{d_3} & \color{red}{\cdots} & \color{red}{d_n}\\ \end{array} \]

红色部分是实际的答案，将问题转化为整个矩阵减去黑色部分，即：

\[S_n=(n+1)\times\sum_{i=1}^nd_i-\sum_{i=1}^{n}id_i \]

使用两个树状数组，一个维护 \(d_i\)，一个维护 \(id_i\)。

AC代码

#include <bits/stdc++.h>
typedef long long ll;

using namespace std;

const int N=1e5+5;
int n, m;
ll a[N], sa[N];

struct BIT {
    ll t[N];
    int lowbit(int x) { return x&-x; }
    void modify(int x, ll d) {
        for (; x <= n; x += lowbit(x)) { t[x] += d; }
    }
    ll pre_sum(int x)
    {
        ll s = 0;
        for (; x; x -= lowbit(x)) { s += t[x]; }
        return s;
    }
} T1, T2;

ll query(int x)
{
    return (x+1)*T1.pre_sum(x) - T2.pre_sum(x);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        sa[i] = sa[i-1] + a[i];
    }
    while (m--) {
        char op; cin >> op;
        if (op == 'Q') {
            int l, r;
            cin >> l >> r;
            cout << sa[r]-sa[l-1]+query(r)-query(l-1) << endl;
        } else {
            int l, r; ll x;
            cin >> l >> r >> x;
            T1.modify(l, x);
            T1.modify(r+1, -x);
            T2.modify(l, l*x);
            T2.modify(r+1, (r+1)*(-x));
        }
    }
}

AT_abc388_D - Coming of Age Celebration

考虑 pull 和 push。

考虑每个人受到前方哪些人送的石头，等价于考虑每个人会送给后方哪些人石头。因为前 \(i-1\) 个人的石头都送完后，第 \(i\) 个人有多少石头自然就能求出来了。

不难发现，push 型的操作可以转化为区间修改+单点查询。具体而言，如果一个人有 \(x\) 块石头，它会给区间 \([i+1,\min(i+x, n)]\) 上每个人都送一块石头。

用树状数组维护即可。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
    int n; 
    vector<int> t;
    BIT(int n): n(n) { t.assign(n+1, 0); }
    int lowbit(int x) {
        return x&-x;
    }
    void modify(int x, int d) {
        for (; x <= n; x += lowbit(x)) { t[x] += d; }
    } 
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) { res += t[x]; }
        return res;
    }
};

int main()
{
    int n; cin >> n;
    BIT t(n);
    vector<int> a(n);
    for (auto &x: a) { cin >> x; }
    for (int i = 1; i <= n; ++i) {
        int now = a[i-1] + t.query(i);
        if (i+1 <= n) { t.modify(i+1, 1); }
        int p = min(i+now, n) + 1;
        if (p <= n) { t.modify(p, -1); }
        a[i-1] = now - (p-i-1);
    }
    for (auto &x: a) { cout << x << " "; }
}

权值树状数组

将值域作为树状数组的下标，称为权值树状数组。

权值树状数组通常结合离散化使用。

P1972 [SDOI2009] HH 的项链

离线处理询问。

每枚举到一个数 \(a_i\)，将上一个数 \(a_i\) 删去，这样剩下多少个数就是答案。

记 \(t_i=0/1\) 表示某个数是否计入答案，每次询问相当于求

\[\sum_{j=l_i}^{r_i}t_j \]

单点修改，区间求和，可以用树状数组维护。

【回溯时删数】是树状数组的一种典型技巧，相似的题目还有 P2982 [USACO10FEB] Slowing down G。

AC代码

#include <bits/stdc++.h>

using namespace std;

const int N=1e6+5;
int n, m, a[N], ans[N], pre[N];
vector <pair<int,int>> q[N];

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

struct BIT {
	int t[N];
	int lowbit(int x) { return x&-x; }
	void modify(int x, int d)
	{
		for (; x <= n; x += lowbit(x)) { t[x] += d; }
	}
	int query(int x)
	{
		int res = 0;
		for (; x; x -= lowbit(x)) { res += t[x]; }
		return res;
	}
} T;

int main()
{
	n = read();
	for (int i = 1; i <= n; ++i) { a[i] = read(); }
	m = read();
	for (int i = 1; i <= m; ++i) {
		int l=read(), r=read();
		q[r].push_back({l,i});
	}
	for (int i = 1; i <= n; ++i) {
		if (pre[a[i]]) { T.modify(pre[a[i]], -1); }
		pre[a[i]] = i;
		T.modify(i, 1);
		for (auto [L, id]: q[i]) {
			ans[id] = T.query(i)-T.query(L-1);
		}
	}
	for (int i = 1; i <= m; ++i) { printf("%d\n", ans[i]); }
}

逆序对

权值树状数组的经典运用是求逆序对。

建立权值树状数组，离散化后每次标记 \(t[a[i]]=1\)。此前已标记的数字下标都小于当前数字，因此 \(a[i]\) 的后缀和（不包括 \(a[i]\)）就是在该点处逆序对的个数。

P1966 [NOIP2013 提高组] 火柴排队

当 \(a[i]\) 与 \(b[i]\) 大小顺序相同（如：213 对 546）时，高度差最小。证明如下：

\[\begin{align} \forall a_i<a_j, b_i<b_j,\\& \left((a_i-b_i)^2 + (a_j-b_j)^2\right) - \left((a_i-b_j)^2 + (a_j-b_i)^2\right)\\ & = -2a_i b_i -2 a_j b_j +2a_ib_j +2a_jb_i \\ & = 2(a_i-a_j)(b_j-b_i) \\ & < 0 \end{align} \]

原问题转化为求伪排序时的逆序对。
定义 \(idx[x]=i\) 表示在 \(a[]\) 中第 \(x\) 小的数字下标为 \(i\)，则 \(b[]\) 中第 \(x\) 小的元素下标也应该变成 \(i\).
建立权值树状数组，每次标记 \(t[i]=1\)，当前已标记的数字都是下标小于当前数字的，因此求 \(T[i:n]\)，答案累加即可。

AC代码

#include <bits/stdc++.h>
typedef long long ll;

using namespace std;

const int N=1e5+5, MOD=1e8-3;
int n, idx[N];
ll a[N], aa[N], b[N], bb[N], ans;

struct BIT {
	ll t[N];
	int lowbit(int x) { return x&-x; }
	void modify(int x, int d) {
		for (; x <= n; x += lowbit(x)) { t[x] += d; }
	} 
	int query(int x)
	{
		ll res = 0;
		for (; x; x -= lowbit(x)) { res += t[x]; }
		return res;
	}
} T;

int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) { cin >> a[i]; aa[i]=a[i]; } sort(aa+1, aa+n+1);
	for (int i = 1; i <= n; ++i) { cin >> b[i]; bb[i]=b[i]; } sort(bb+1, bb+n+1);
	for (int i = 1; i <= n; ++i) {
		int x = lower_bound(aa+1, aa+n+1, a[i])-aa;
		idx[x] = i;
	}
	for (int i = 1; i <= n; ++i) {
		int x = lower_bound(bb+1, bb+n+1, b[i])-bb;
		ans = (ans + T.query(n)-T.query(idx[x])) % MOD;
		T.modify(idx[x], 1);
	}
	cout << ans << endl;
}

最长上升子序列

权值树状数组的另一个典型运用是求解最长上升子序列（LIS）。

以下仅讨论 \(O(n\log n)\) 的求解方法，\(O(n^2)\) 的 DP 基础省略。

离散化后建立权值树状数组，以 \(a[i]\) 结尾的最长上升子序列长度存入 \(t[a[i]]\)，每次求出以早于 \(a[i]\) 出现的且小于 \(a[i]\) 的值结尾的最长上升子序列长度，再加一就是当前位置的答案，即

\[\max_{1\leq k< i}{t[a[k]]}+1 \]

模板题见 B3637 最长上升子序列。以下为参考代码：

#include <bits/stdc++.h>

using namespace std;

const int N=1e5+5;
int n, a[N], aa[N], f[N], ans;

struct BIT {
    int t[N];
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d)
    {
        for (; x <= n; x += lowbit(x)) { t[x] = max(t[x], d); }
    }
    int query(int x)
    {
        int res = 0;
        for (; x; x -= lowbit(x)) { res = max(res, t[x]); }
        return res;
    }
} T;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i) { cin >> a[i]; aa[i]=a[i]; }
    sort(aa+1, aa+n+1);
    f[0] = 0;
    for (int i = 1; i <= n; ++i) {
        int x = lower_bound(aa+1, aa+n+1, a[i])-aa;
        f[i] = T.query(x-1) + 1;
        T.modify(x, f[i]);
        ans = max(ans, f[i]);
    }
    cout << ans << endl;
}

AT_abc393_f

可以用树状数组在 \(O(n\log n)\) 内求出 LIS。

离线所有询问，不难发现询问 \((r,x)\) 就是在问区间 \([1,r]\) 上以不大于 \(x\) 的数作为结尾的 LIS 长度。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
    int n;
    vector<int> t;
    BIT(int n): n(n) { t.assign(n+1, 0); }
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x+=lowbit(x)) { t[x] = max(t[x], d); }
    }
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) { res = max(res, t[x]); }
        return res;
    }
};

void solve()
{
	int n, q;
    cin >> n >> q;
    vector<int> a(n), b, ans(q);
    vector<array<int,3>> qu(q);
    for (auto &x: a) { cin >> x; b.push_back(x); }
    for (int i = 0; i < q; ++i) {
        cin >> qu[i][0] >> qu[i][1];
        qu[i][2] = i;
        b.push_back(qu[i][1]);
    }
    sort(qu.begin(), qu.end());
    sort(b.begin(), b.end());
    b.erase(unique(b.begin(), b.end()), b.end());
    BIT t(b.size());
    int now = 0;
    for (auto [r, x, id]: qu) {
        while (now < r) {
            int pos = lower_bound(b.begin(), b.end(), a[now])-b.begin()+1;
            int res = 1;
            if (pos-1) { res = t.query(pos-1) + 1; }
            t.modify(pos, res);
            ++now;
        }
        int ask = lower_bound(b.begin(), b.end(), x)-b.begin()+1;
        ans[id] = t.query(ask);
    }
    for (auto x: ans) { cout << x << "\n"; }
}

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int t = 1;
	while (t--) { solve(); }
}

gym104945A. Card game

讨论 \(P_4^4=24\) 中颜色的排序，对于每种情况，操作数为 \(n-\rm{LIS}\)。

AC代码

#include <bits/stdc++.h>

using namespace std;

const int N=1e5+5;
int n, v[5], w[N], ans=INT_MAX;

struct BIT {
    int t[N];
    int lowbit(int x) { return x&(-x); }
    void clear()
    {
        for (int i = 1; i <= n; ++i) { t[i] = 0; }
    }
    void modify(int x, int d)
    {
        for (; x <= n; x += lowbit(x)) { t[x] = max(t[x], d); }
    }
    int query(int x)
    {
        int mx = 0;
        for (; x; x -= lowbit(x)) { mx = max(mx, t[x]); }
        return mx;
    }
} T;

struct card {
    char tp;
    int num;
} c[N];

int co_to_id(char x)
{
    switch (x) {
        case 'S': return 1;
        case 'W': return 2;
        case 'E': return 3;
        case 'R': return 4;
        case 'C': return 5;
        default: return -1;
    }
}

void solve()
{
    for (int i = 1; i <= n; ++i) { w[i] = i; }
    sort(w+1, w+n+1, [](int a, int b){
        return (
            (v[co_to_id(c[a].tp)] < v[co_to_id(c[b].tp)]) 
            || (v[co_to_id(c[a].tp)] == v[co_to_id(c[b].tp)] && c[a].num<c[b].num)
        );
    });
    T.clear();
    int res = 1;
    for (int i = 1; i <= n; ++i) {
        int f = T.query(w[i])+1;
        res = max(res, f);
        T.modify(w[i], f);
    }
    ans = min(ans, n-res);
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        string x; cin >> x;
        c[i].tp = x[0];
        c[i].num = stoi(x.substr(1,(int)x.length()-1));
    }
    for (int i = 1; i <= 4; ++i) { v[i] = i-1; }
    do {
        solve();
    } while (next_permutation(v+1, v+5));
    cout << ans << endl;
}

偏序问题

生活中有很多情景需要进行多维度比较，比如同时比较两名运动员的耐力和爆发力。此时经常出现类似 \(A\) 的耐力强，但 \(A\) 的爆发力不如 \(B\) 的情况。我们一般会认为两人各有长处，没有绝对的高下之分。

这种情况下，我们称集合中的元素建立了偏序关系。诸如统计满足 \(\begin{cases}a_i<a_j\\b_i>b_j\end{cases}\) 的二元组 \((i,j)\) 的问题，称为偏序问题。

树状数组常应用于解决偏序问题，比如逆序对就是对 \(\begin{cases}i<j\\a_i>a_j\end{cases}\) 的二元组 \((i,j)\) 进行计数，LIS 就是通过对 \(j\) 求出所有满足 \(\begin{cases}i<j\\a_i<a_j\end{cases}\) 的二元组 \((i,j)\) 中的 \(\max(f_i)\) 进行转移。更多应用详见例题。

gym104875J. Justice Served

偏序问题。

先按左端点从小到大排序，再按右端点从大到小排序。此时按顺序遍历就可以从大到小地访问每一个区间。

对右端点离散化后开权值树状数组，后缀最大值再 \(+1\) 即为答案。

AC代码

#include <bits/stdc++.h>

using namespace std;

const int N=2e5+5;
int n, a[N], b[N], p[N], tot, id[N], c[N];

struct BIT {
    int t[N];
    int lowbit(int x) { return x&(-x); }
    void modify(int x, int d)
    {
        for (; x <= n; x += lowbit(x)) { t[x] = max(t[x], d); }
    }
    int query(int x)
    {
        int mx = 0;
        for (; x; x -= lowbit(x)) { mx = max(mx, t[x]); }
        return mx;
    }
} T;

int pos_to_id(int pp)
{
    return lower_bound(p+1, p+tot+1, pp, greater<int>())-p;
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i] >> b[i];
        p[i] = b[i] = a[i]+b[i]-1;
        
    }
    sort(p+1, p+n+1, greater<int>()); tot=unique(p+1,p+n+1)-(p+1);
    for (int i = 1; i <= n; ++i) { id[i] = i; }
    sort(id+1, id+n+1, [](int x, int y){
        return a[x]<a[y] || (a[x]==a[y] && b[x]>b[y]);
    });
    for (int i = 1; i <= n; ++i) {
        c[id[i]] = T.query(pos_to_id(b[id[i]])) + 1;
        T.modify(pos_to_id(b[id[i]]), c[id[i]]);
    }
    for (int i = 1; i <= n; ++i) { cout << c[i]-1 << " "; }
}

P5200 [USACO19JAN] Sleepy Cow Sorting G

将 \(p\) 从右端向左的单调减部分划为一组，剩下部分划作另一组。
显然，左侧不满足单调性的部分都需要移动，非单调部分的长度即为操作数。

例如样例：1 2 4 3，满足单调性的部分只有 3，剩下的 1 2 4 都需要移动

对于 1，需要跨过 2 4，并放在单调部分的对应位置
单调部分的对应位置，即求单调部分左侧有多少数小于 1（显然没有）
所以 1 需要移动 \(2\) 步，此时 \(p\) 变为 2 4 1 3

同理对于 2，先移动 \(1\) 步跨过 4，单调部分有一个数 1 小于 4，就再走一步，共 2 步
此时 \(p\) 变为 4 1 2 3

同理对于 4，不用额外移动跨过非单调部分（因为只有它自己）
单调部分有三个数 1 2 3 比它小，所以再走 \(3\) 步，总共走 \(3\) 步，\(p\) 变为 1 2 3 4

上述步骤中，对于一个数 \(x\)，每次需要计算：

跨过非单调部分所需步数（非单调部分长度减 \(1\)）
单调部分左侧比 \(x\) 小的数的个数，可以用树状数组维护

AC代码

#include <bits/stdc++.h>

using namespace std;

const int N=1e5+5;
int n, a[N], k=1;

struct BIT {
	int t[N];
	int lowbit(int x) { return x&-x; }
	void modify(int x, int d)
	{
		for (; x <= n; x += lowbit(x)) { t[x] += d; }
	}
	int query(int x)
	{
		int res = 0;
		for (; x; x -= lowbit(x)) { res += t[x]; }
		return res;
	}
} T;

int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) { cin >> a[i]; }
	for (int i = n; i; --i) {
		T.modify(a[i], 1);
		if (a[i-1] > a[i]) {
			k = i-1; break;
		}
	}
	cout << k << endl;
	for (int i = 1; i <= k; ++i) {
		cout << k-i+T.query(a[i]) << " ";
		T.modify(a[i], 1);
	}
}

iai405. 铁人三项

三维偏序问题，先通过从大到小排序消去 \(x\)，再用一个数组，\(y\) 作为下标，\(z\) 作为值。

如果一个运动员，存在一个运动员比他先出现（\(x\) 比他大）下标比他大（\(y\) 比他大）值比他大（\(z\) 比他大），那么这个运动员就是无用的。

此时，问题转换为后缀最值，可用树状数组，同时使用 \(n-y\) 作为下标转换为前缀最值。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
	int n;
    vector <int> t;
    BIT(int n): n(n) { t.resize(n+1, 0); }
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x += lowbit(x)) { t[x] = max(t[x], d); }
    }
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) { res = max(res, t[x]); }
        return res;
    }
};

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int n; cin >> n;
	vector<array<int,3>> p(n);
	for (auto& [x, y, z]: p) { cin >> x >> y >> z; y=n-y+1; }  // +1 防止因修改 0 导致 TLE
	sort(p.begin(), p.end(), greater<array<int,3>>());
	BIT t(n);
	int ans = n;
	for (auto [x, y, z]: p) {
		if (t.query(y-1) > z) { --ans; }
		t.modify(y, z);
	}
	cout << ans << "\n";
}

P2344 [USACO11FEB] Generic Cow Protests G

\(O(n^2)\) 分组 DP 是显然的。

记前缀和数组为 \(s_i\)，前 \(i\) 头牛分组的方案数为 \(f_i\)，当 \([j+1,i]\) 的和不小于 \(0\) 时 \([j+1,i]\) 可被分为一组，此时方案数为 \(f_j\)，则

\[f_i=\displaystyle\sum_{j=1}^{i-1}f_j[s_i-s_j\geq0] \]

考虑优化求和式。将前缀和改写为 \(s_i\geq s_j\)，就是一个典型的偏序问题。

将 \(s_i\) 作为权值数组的下标，\(t[s_i]=f_i\)，原求和式等价于求 \(t\) 中 \(s_i\) 处的前缀和。

单点修改，区间求和，用树状数组维护即可。

AC代码

#include <bits/stdc++.h>

using namespace std;
const int MOD = 1e9+9;
typedef long long ll;

struct BIT {
	int n;
    vector <ll> t;
    BIT(int n): n(n) { t.resize(n+1, 0); }  // 注意值域树状数组中 n=tot
    int lowbit(int x) { return x&-x; }
    void modify(int x, ll d) {
        for (; x <= n; x += lowbit(x)) { t[x] += d; }
    }
    ll query(int x) {
        ll res = 0;
        for (; x; x -= lowbit(x)) { res += t[x]; }
        return res;
    }
};

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int n; cin >> n;
    vector<int> a(n+1), s(n+1), p;
    vector<ll> f(n+1);
    p.push_back(0);
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        s[i] = s[i-1] + a[i];
        p.push_back(s[i]);
    }
    sort(p.begin(), p.end());
    p.erase(unique(p.begin(),p.end()), p.end());
    BIT t(p.size());
    for (int i = 0; i <= n; ++i) {
        int id = lower_bound(p.begin(), p.end(), s[i])-p.begin()+1;
        f[i] = i>0? t.query(id) % MOD: 1;
        t.modify(id, f[i]);
    }
    cout << f[n] << "\n";
}

iai100. 132型序对

固定看 \(\texttt{1}\)、看 \(\texttt{3}\)、看 \(\texttt{2}\)，都不行。因此采用补集思想，先算 \(\texttt{123}+\texttt{132}\) 的数量，再减 \(\texttt{123}\) 的数量：

对于 \(\texttt{123}+\texttt{132}\) 的数量，固定看 \(\texttt{1}\)，找到比 \(\texttt{1}\) 后出现的、两个更大的数字，组成数对。

对于 \(\texttt{123}\) 的数量，固定看 \(\texttt{2}\)，找到比 \(\texttt{2}\) 早出现的、更小的数字，和比"\(\texttt{2}\) 晚出现的、更大的数字。

因此，可以考虑可以从前往后，从后往前对 \(a\) 各扫一遍，构建树状数组统计比 \(a_i\) 早出现的、更小的数字和比 \(a_i\) 晚出现的、更大的数字，将答案分别记录在 \(pre[]\) 和 \(suf[]\) 中，则答案为：

\[\sum_{i=1}^n\left( C_{suf[i]}^{2} - pre[i]\times suf[i]\right) \]

AC代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

struct BIT {
	int n;
    vector <int> t;
    BIT(int n): n(n) { t.resize(n+1, 0); }  // 注意值域树状数组中 n=tot
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x += lowbit(x)) { t[x] += d; }
    }
	// 前缀和
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) { res += t[x]; }
        return res;
    }
};

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int n; cin >> n;
	vector<int> a(n+1), pre(n+1), suf(n+1), b;
	for (int i = 1; i <= n; ++i) { cin >> a[i]; b.push_back(a[i]); }
	sort(b.begin(), b.end());
	b.erase(unique(b.begin(), b.end()), b.end());
	// 求 pre[]
	BIT t(n);
	for (int i = 1; i <= n; ++i) {
		int id = lower_bound(b.begin(), b.end(), a[i])-b.begin()+1;
		pre[i] = t.query(id-1);
		t.modify(id, 1);
	}
	// 求 suf[]
	t = BIT(n);
	for (int i = n; i; --i) {
		int id = lower_bound(b.begin(), b.end(), a[i])-b.begin()+1;
		suf[i] = (n-i+1)-t.query(id);
		t.modify(id, 1);
	}
	// 计算答案
	ll ans = 0;
	for (int i = 1; i <= n; ++i) {
		ans += 1LL*suf[i]*(suf[i]-1)/2 - pre[i]*suf[i];
	}
	cout << ans << "\n";
}

树状数组上倍增

求第一个前缀和等于 \(x\) 的位置，可以使用二分套树状数组在 \(O(\log^2n)\) 的时间内完成。

而由于树状数组天然具有二分的结构，我们也可以直接在树状数组上倍增。

^[2:1]

考虑找到最后一个前缀和严格小于 \(x\) 的位置，加一即为答案。

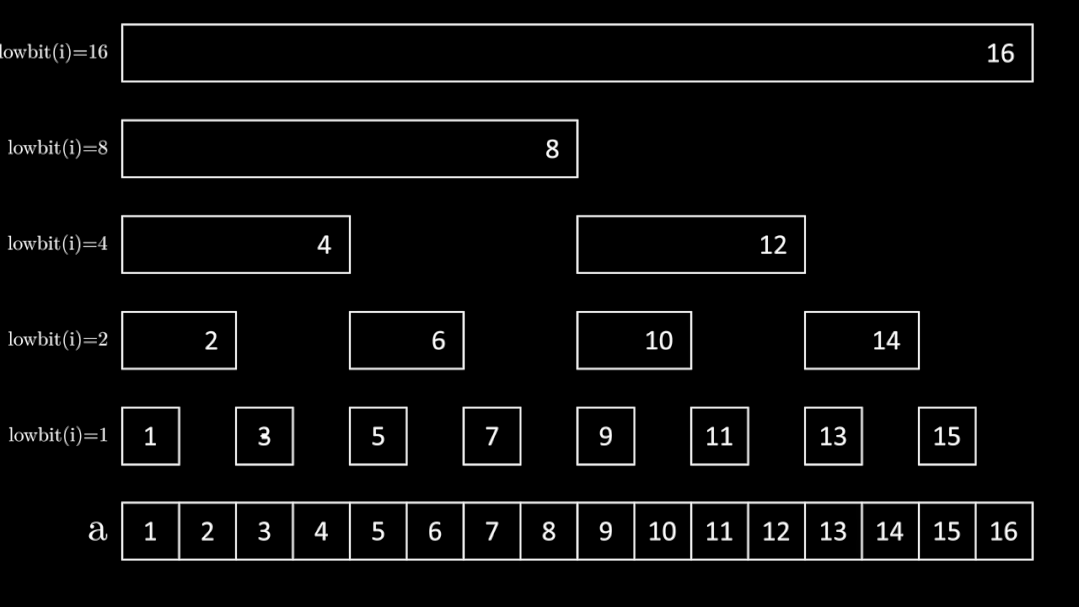
继续从树状数组的结构出发。树状数组是一棵天然的二叉搜索树，二分的过程可以看作：检查左儿子的终点处前缀和是否严格小于 \(x\)，如果小于，则进入右儿子，否则进入左儿子。

记此时父节点的长度为 \(2^{k+1}\)。虽然实际情况中，这个节点的右儿子被隐藏掉了，但我们仍然通过可以让下标加 \(2^k\) 的方式到达其长度为 \(2^k\) 的左儿子的终点，达成“跳过左儿子”的效果。

比如在上图中，考虑从下标为 \(0\) 开始，以长度为 \(2^4=16\) 的 \(16\) 号节点作为父节点，如果此时其左儿子终点 \(8\) 的前缀和严格小于 \(x\)，说明答案处于右子区间 \([9,16]\)，我们可以令下标加 \(2^3=8\) 等价地进入右子区间，否则继续处在下标为 \(0\) 的位置，等价于进入左子区间。

将树状数组还原为线段树，树状数组上倍增和线段树二分是完全等价的。因此，虽然对任意的 \(x\)，\(t[x+2^k]\) 并不总包含了区间 \([x+1,x+2^k]\) 的信息，但我们可以保证在倍增过程中所遍历到的 \((x,k)\) 都是满足这一性质的，我们只需要将 \(+2^k\) 的操作看作跳过左儿子即可。树状数组真是太奇妙了~

单次查询时间复杂度为 \(O(\log n)\)。参考代码如下：

// 求最小的前缀和等于x的位置
int select(int x) {
    int ans = 0, sum = 0;
    for (int i = I; i >= 0; --i) {
        if (ans+(1<<i) <= n && sum+t[ans+(1<<i)] < x) { 
            ans += 1<<i;
            sum += t[ans];
        }
    }
    return ans + 1;
}

维护第 \(k\) 大的数字，或者说求剩余数组中下标为 \(k\) 的数字，是树状数组上倍增的经典运用，详见例题。

gym104945K. Team selection

题意可化为：对一个初值为 \(1\) 到 \(m\) 的数组，维护两种操作：①查询第 \(a_i,b_i\) 位的元素，②删除一个元素。

设权值数组 \(t[i]=\begin{cases}1&i尚未删去\\0&i已经删去\end{cases}\)，查询剩余的第 \(k\) 位的元素等价于在 \(t\) 中找到第一个前缀和等于 \(k\) 的位置，可以直接在树状数组上二分完成。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
    int n;
    vector<int> t;
    BIT(int n): n(n) { t.assign(n+1, 0); }
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x+=lowbit(x)) { t[x] += d; }
    }
    int select(int x) {
        int ans = 0, sum = 0;
        for (int i = ceil(log2(n)); i >= 0; --i) {
            if (ans+(1<<i) <= n && sum+t[ans+(1<<i)] < x) {
                ans += 1<<i;
                sum += t[ans];
            }
        }
        return ans + 1;
    }
};

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int m; cin >> m;
    BIT t(m);
    for (int i = 1; i <= m; ++i) { t.modify(i, 1); }
    vector<int> a(m/2+1), b(m/2+1);
    for (int i = 1; i <= m/2; ++i) { cin >> a[i]; }
    for (int i = 1; i <= m/2; ++i) { cin >> b[i]; }
    for (int i = 1; i <= m/2; ++i) {
        a[i] = t.select(a[i]); t.modify(a[i], -1);
        b[i] = t.select(b[i]); t.modify(b[i], -1);
    }
    for (int i = 1; i <= m/2; ++i) { cout << a[i] << " \n"[i==m/2]; }
    for (int i = 1; i <= m/2; ++i) { cout << b[i] << " \n"[i==m/2]; }
}

AT_abc392_f

从后往前处理排位。数字 \(n\) 的位置为 \(p_n\)，数字 \(n-1\) 的位置为剩下位置中的 \(p_{n-1}\)，以此类推……

记权值数组 \(t[i]=0/1\) 表示第 \(i\) 个位置已/未被占，“剩下位置中的第 \(x\) 个”等价于第一个前缀和等于 \(x\) 的位置，用树状数组倍增维护即可。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
    int n;
    vector<int> t;
    BIT(int n): n(n) { t.assign(n+1, 0); }
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x+=lowbit(x)) { t[x] += d; }
    }
    int query(int x) {
        int res = 0;
        for (; x; x-=lowbit(x)) { res += t[x]; }
        return res;
    }
    int select(int x) {
        int ans = 0, sum = 0;
        for (int i = ceil(log2(n)); i >= 0; --i) {
            if (ans+(1<<i) <= n && sum + t[ans+(1<<i)] < x) {
                ans += 1<<i;
                sum += t[ans];
            }
        }
        return ans + 1;
    }
};

void solve()
{
	int n; cin >> n;
    vector<int> p(n+1), a(n+1);
    for (int i = 1; i <= n; ++i) { cin >> p[i]; }
    BIT t(n);
    for (int i = 1; i <= n; ++i) { t.modify(i, 1); }
    for (int i = n; i; --i) {
        int pos = t.select(p[i]);
        a[pos] = i;
        t.modify(pos, -1);
    }
    for (int i = 1; i <= n; ++i) { cout << a[i] << " \n"[i==n]; }
}

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
	int t = 1;
	while (t--) { solve(); }
}

P3988 [SHOI2013] 发牌

销牌的操作只会将牌堆顶的牌移到堆底，等价于将原数组看作一个环，在环上向前走了一步。破环为链，将数组复制一份接在末尾，用一个 \(1\leq p\leq n\) 的指针指向开头的位置，记 \(m\) 为此时牌堆的大小，从 \(p\) 往后的 \(m\) 张牌就是此时的牌堆。如：

\[[1,2,3,4],1,2,3,4\to1,2,[3,4,1,2],3,4 \]

此时如果进行发牌操作，发出的就是原始牌堆中剩余的第 \(p\) 张。

从而，单次销牌的操作转换为了 \(p\leftarrow (p+R_i)\%m\)，其中 \(m\) 表示牌堆此时的大小。题目转换为，维护剩余的原始牌堆，查询其中的第 \(p\) 张牌并将其删去。

设权值数组 \(t[i]=\begin{cases}1&a_i尚未删去\\0&a_i已经删去\end{cases}\)，查询剩余的第 \(p\) 张牌等价于在 \(t\) 中找到第一个前缀和等于 \(p+1\) 的位置（注意 \(p\) 从 \(0\) 开始），可以直接在树状数组上二分完成。

AC代码

#include <bits/stdc++.h>

using namespace std;

struct BIT {
    int n;
    vector<int> t;
    BIT(int n): n(n) { t.assign(n+1, 0); }
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x+=lowbit(x)) { t[x] += d; }
    }
    int select(int x) {
        int ans = 0, sum = 0;
        for (int i = ceil(log2(n)); i >= 0; --i) {
            if (ans+(1<<i) <= n && sum+t[ans+(1<<i)] < x) { 
                ans += 1<<i;
                sum += t[ans];
            }
        }
        return ans + 1;
    }
};

int main()
{
	cin.tie(nullptr)->sync_with_stdio(false);
    int n; cin >> n;
    BIT t(n);
    for (int i = 1; i <= n; ++i) { t.modify(i, 1); }
    int p = 0;
    for (int m = n; m; --m) {
        int R; cin >> R;
        p = (p + R) % m;
        int id = t.select(p+1);
        cout << id << "\n";
        t.modify(id, -1);
    }
}

总结

以下给出个人封装后的模板。

struct BIT {
    int n;
    vector <int> t;
    BIT(int n): n(n) { t.resize(n+1, 0); }  // 注意值域树状数组中 n=tot
    int lowbit(int x) { return x&-x; }
    void modify(int x, int d) {
        for (; x <= n; x += lowbit(x)) { t[x] += d; }
    }
    // 前缀和
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) { res += t[x]; }
        return res;
    }
    // 求最小的前缀和等于x的位置
    int select(int x) {
        int ans = 0, sum = 0;
        for (int i = ceil(log2(n)); i >= 0; --i) {
            if (ans+(1<<i) <= n && sum+t[ans+(1<<i)] < x) { 
                ans += 1<<i;
                sum += t[ans];
            }
        }
        return ans + 1;
    }
};
BIT T(n);

例题汇总如下：

题目	备注
243. 一个简单的整数问题2	区间修改+区间查询模板题
AT_abc388_D - Coming of Age Celebration	思维题，区间修改+单点查询
P1972 [SDOI2009] HH 的项链 P2982 [USACO10FEB] Slowing down G	回溯时删数
P1966 [NOIP2013 提高组] 火柴排队	思维题+逆序对模板
AT_abc393_f	LIS 模板拓展
gym104945A. Card game	思维题+LIS 模板
gym104875J. Justice Served	偏序问题
P5200 [USACO19JAN] Sleepy Cow Sorting G	思维题，权值树状数组
iai405. 铁人三项	三维偏序模板
P2344 [USACO11FEB] Generic Cow Protests G	树状数组优化 DP
iai100. 132型序对	计数题，权值树状数组
gym104945K. Team selection	树状数组上倍增模板题
AT_abc392_f	树状数组上倍增
P3988 [SHOI2013] 发牌	思维题，树状数组上倍增

图片摘自【学习笔记】详解线段树(浅显易懂,匠心之作,图文并茂) ↩︎
图片摘自什么是树状数组？让这个12岁年轻人为你讲解 ↩︎ ↩︎

posted @ 2025-02-04 12:03 LittleDrinks 阅读(26) 评论(0) 编辑收藏举报

刷新页面返回顶部

引入

lowbit 操作

树状数组的结构

基本操作及模板

权值树状数组

逆序对

最长上升子序列

偏序问题

树状数组上倍增

总结

公告