20240119方程图像研究
事情起因:

研究人:csj、lqy、xzq、yjf
前言
方程 \(f(x,y)=0\) 的图像相比函数更为抽象,它同时涉及 \(x,y\) 两个参数,没有“一个 \(x\) 对应一个 \(y\)”的限制,可能具有高次项(如 \(x^4\))、交叉项(如 \(xy\))等复杂的形式。在这种情况下,对方程图像研究的研究策略显得尤为重要。
方程图像研究要求:
- 描点法画图(使用卡西欧),在 \(x\) 轴上任取值,对于给定 \(x_0\),应在有限时间内求出所有对应的 \(y\)。
- 草图绘制(直接绘制):综合方程性质(如定义域、单调性、对称性),明确区间单调性及端点,利用对称性作图、或化归为已知方程并求出其参数。
- 精准图像绘制(使用 Geogebra):已知 Geogebra 可以绘制关于两个参数 \(x,y\) 方程 \(f(x,y)=0\) 的图像,所有研究最后应经过检验。
下文将先以 \(x^4+y^4=x^2+y^2\)、\(11x^2+10xy+3y^2+4x+4y=0\) 为例,按照上述要求进行探索,罗列对图像研究有所帮助的思路,并在最后对思路进行复盘。
Q1:方程 \(x^4+y^4=x^2+y^2\)
描点法
设 \(t=y^2\),以 \(x\) 作为参数,移项得:\(t^2-t+(x^4-x^2)=0\)。
对于给定的一个 \(x_0\in R\),可以利用卡西欧求解四次方程,或手动(卡西欧)求解二次方程,得到对应这个 \(x_0\) 的所有 \(y\) 值。
草图绘制
第一,观察到原方程中所有 \(x,y\) 都是平方或四次方,因此考虑对称性。取 \(P(x,y)\in \text{I}\),将 \(P'(-x,y)\) 代入原方程,易得原方程依然成立。同理可知 \((x,-y),(-x,-y)\) 同样成立。于是原方程的图像关于原点对称(坐标轴上的点也满足)。 接下来,我们只需要研究它第一象限(含两条坐标轴正半轴,下文同)的图像即可。
第二,观察到原方程的形式非常对称(\(x,y\) 完全可以交换),于是可以进一步研究它的对称性。取 \(P(x,y)\in \text{I}\),\(Q(y,x)\) 也满足方程,所以它第一象限的图像关于直线 \(y=x\) 对称。 接下来,我们只需要研究它第一象限在直线 \(y=x\) 上方的部分(\(y>x\))即可。
第三,联想到圆的方程,可以进行配方,得到 \(\displaystyle(x^2-\frac12)^2+(y^2-\frac12)^2=\frac12\)。
第四,由于其关于原点对称,想到使用极坐标。设 \(\begin{cases}x=\rho\cos\theta\\ y=\rho\sin\theta\end{cases}\),则 \(x^2+y^2=\rho^2\)。代入化简得到:\(\rho^2(\cos^4\theta+\sin^4\theta)=1\)。进一步化简得到:\(\rho^2=\displaystyle\frac{1}{1-\frac12\sin^22\theta}\),可以形象地知道:方程在第一象限的图像类似于一个圆的一部分。
第五,原方程可以把 \(x,y\) 分开(即不包含 \(x^ay^b\) 项),移项得到 \(x^4-x^2=-(y^4-y^2)\)。观察到移项后两侧具有相同的形式。于是可以设 \(f(a)=a^4-a^2\),图像上任意一点 \(P(x,y)\) 均满足 \(f(x)=-f(y)\)。
通过标根法我们可以画出 \(f(a)\) 的图像。
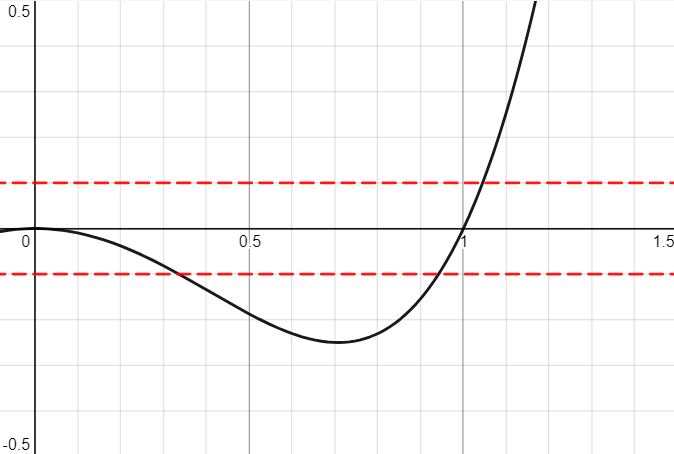
按照上文的思路,为研究原方程在第一象限且 \(y>x\) 的图像,我们观察 \(f(a)\) 图像 \([0,+\infty)\) 的部分,并且取 \(y_0\in[1,+\infty)\),在图像上画出 \(y=f(y_0)\) 和 \(y=-f(y_0)\) 两条平行于 \(x\) 轴的直线。我们容易得到以下两条结论:
- 这部分图像,一个 \(y_0\) 对应两个 \(x_0\),原方程图像的趋势是先增后减,记 \(f(a)\) 在 \((0,1)\) 上的极值点为 \(x_a\),则原方程图像在 \(x_a\) 处取得最大值
- \(x\) 的取值是有限的,并且 \(y\) 的取值范围也是有限的
进一步,我们希望求出 \(f(a)\) 在 \((0,1)\) 上的那个极小值点。求导得 \(f'(a)=4a^3-2a=a(4a^2-2)=0\Rightarrow a=\displaystyle\frac{\sqrt 2}{2}\)。因此,原函数的这部分图像在 \([0,\displaystyle\frac{\sqrt2}{2}]\) 严格增,在 \([\displaystyle\frac{\sqrt2}{2},1]\) 严格减,使用在“描点法”中提到的求 \(y\) 的方法,求得:最高点 \((\displaystyle\frac{\sqrt2}{2},1.0986841134678111)\),最低点 \((0,1),(1,1)\)。
或配方,\(\displaystyle(x^2-\frac12)^2+(y^2-\frac12)^2=\frac12\),当 \(x=\displaystyle\frac{\sqrt2}{2}\) 时,\(\displaystyle(x^2-\frac12)^2=0\),此时有 \(y\) 的最大值 \(\displaystyle\sqrt{\sqrt{\frac12}+\frac12}\)。
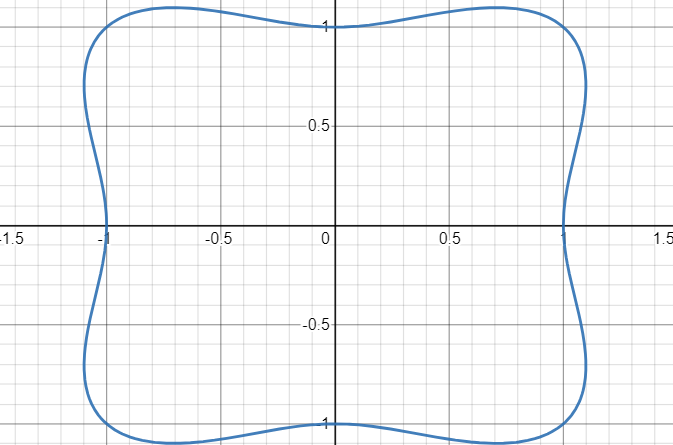
最后,根据上文的对称性,我们可以画出原方程的图像。形象地说,是以 \((-1,1),(-1,-1),(1,1),(1,-1)\) 为顶点的正方形向外胖出一点点。
精确图像绘制
复盘
Q2:方程 \(11x^2+10xy+3y^2+4x+4y=0\)
描点法
对于任意给定的 \(x_0\),代入,能得到一个关于 \(y\) 的一元二次方程,求解即可得到对应 \(x_0\) 的两个 \(y_0\)。
草图绘制
第一,取图像上一点 \(P(x,y)\),代入 \(P(-x,y)\) 等易得:原方程不关于原点或对称轴对称。
第二,原方程左侧不带常数项,显然必过 \((0,0)\)。
第三,联想到形如 \(Ax^2+Bxy+Cy^2+Dx+Ey+F\) 的式子可以由两个带 \(x,y\) 的一次式子相乘得到,如 \((x+y+1)^2\),故猜测可能是两条直线。
接下来我们可以解方程验证这一想法。先整理方程得:\(11x^2+(10y+4)x+3y^2+4y=0\),计算 \(\Delta=(10y+4)^2-44(3y^2+4y)=-32y^2-96y+16\)。显然,\(y\) 不可能取遍一切实数,因而不可能是直线。
(可以通过取两个 \(x\) 确定 4 个 \(y\),组成 2 条直线,然后取第三个点代入验证,同样可以否定两条直线的想法。但这样计算过于繁琐,因此开始考虑直接求 \(\Delta\),观察是否可以求得比较简单的特殊点,进而发现 \(y\) 不可取遍一切实数这一性质。)
同理主元 \(y\),易得 \(x\) 也不可能取遍一切实数,因而原方程的图像必然是一个有限的封闭图形。
上网查资料,二次曲线 \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) 是圆锥曲线,由此继续研究。根据上文所得“有限封闭图形”,原方程的图像只能是椭圆经过平移与旋转后所得。
此外,通过求 \(x\) 和 \(y\) 的范围。可以发现 \(\displaystyle x\in[\frac{1-\sqrt{\Delta_1}}{2},\frac{1+\sqrt{\Delta_1}}{2}]\),其取值范围关于 \(\displaystyle\frac12\) 对称;\(\displaystyle y\in[\frac{-3-\sqrt{\Delta_2}}{2}, \frac{-3+\sqrt{\Delta_2}}{2}]\),其取值范围关于 \(-\displaystyle\frac{3}{2}\) 对称。显然,最左侧和最右侧的点关于对称中心对称,最上面和最下面的点也关于对称中心对称,于是对称中心为 \(\displaystyle(\frac12,-\frac32)\)。
通过把原方程中 \(x\) 换为 \(x+\displaystyle\frac12\),把 \(y\) 换成 \(y-\displaystyle\frac32\),易得平移前的方程为:\(11x^2+3y^2+10xy-2=0\)。
接下来求旋转角和原椭圆方程。
设旋转前椭圆上一点为 \(P(x,y)\),旋转后椭圆 \(11x^2+3y^2+10xy-2=0\) 上的一点为 \(Q(x',y')\),设 \(d=\left|\vec{OP}\right|=\left|\vec{OQ}\right|\),\(\vec{OP}\) 与 \(x\) 轴正半轴的夹角为 \(\alpha\)。设原椭圆向逆时针旋转 \(\theta\in(0,\pi]\),并且 \(\left<\vec{OP},\vec{OQ}\right>=\theta\)。
则有 \(\begin{cases}x=d\cos\alpha\\ y=d\sin\alpha\\ x'=d\cos(\alpha+\theta)\\ y'=d\sin(\alpha+\theta)\end{cases}\),两角正弦和公式展开得 \(\begin{cases}x'=d(\cos\alpha\cos\theta-\sin\alpha\sin\theta)\\ y'=d(\sin\alpha\cos\theta+\cos\alpha\sin\theta)\end{cases}\),将 \(x,y\) 代入得 \(\begin{cases}x'=x\cos\theta-y\sin\theta\\ y'=x\sin\theta+y\cos\theta\end{cases}\)。(此处参考知乎)
将 \((x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)\) 代入旋转后的方程:\(11(x\cos\theta-y\sin\theta)^2+3(x\sin\theta+y\cos\theta)^2+10(x\cos\theta-y\sin\theta)(x\sin\theta+y\cos\theta)=2\)。
化简,即可用 \(\theta\) 表示旋转前的方程:
- \(x^2\) 项: \((11\cos^2\theta+3\sin^2\theta+10\cos\theta\sin\theta)x^2\)
- \(y^2\) 项:\((11\sin^2\theta+3\cos^2\theta-10\cos\theta\sin\theta)y^2\)
- \(xy\) 项:\((-8\sin2\theta+10\cos2\theta)xy\)
- 常数项:\(-2\)
由于旋转前的方程是标准方程,所以 \(xy\) 项的系数 \(\displaystyle -8\sin2\theta+10\cos2\theta=0\Rightarrow\tan2\theta=\frac54\Rightarrow \theta=90°\times k + \frac12\arctan\frac54\ (k\in Z)\)。
当 \(\displaystyle\theta=\frac12\arctan\frac54\) 时,原椭圆方程约为 \(13.4x^2+0.59y^2=2\)。
当 \(\displaystyle\theta=90°+\frac12\arctan\frac54\) 时,原椭圆方程约为 \(0.59x^2+13.4y^2=2\)。
这两者旋转后的结果是一致的。
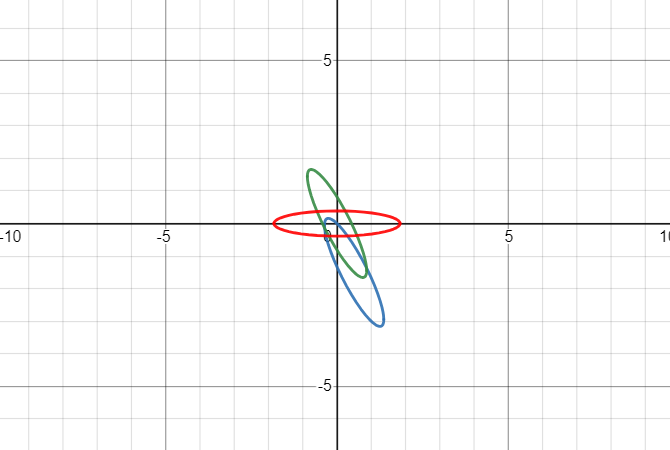
综上,原方程的图像是椭圆 \(0.59x^2+13.4y^2=2\) 逆时针旋转 \(\displaystyle\frac12\arctan\frac54\approx25.04°\) 后向 \(\displaystyle(\frac12,-\frac32)\) 平移后所得。
精确图像绘制
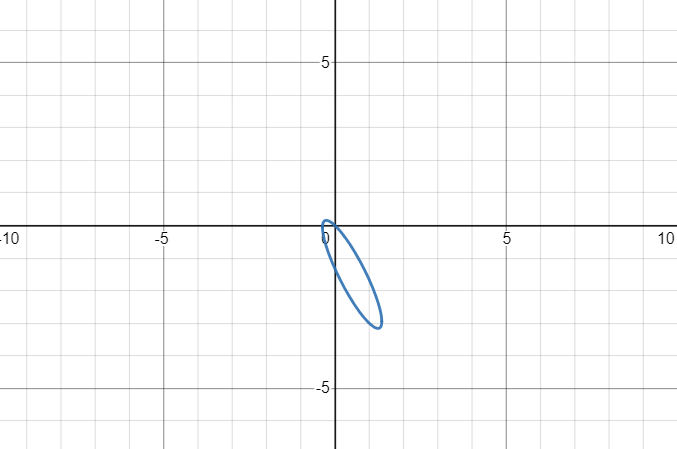
复盘
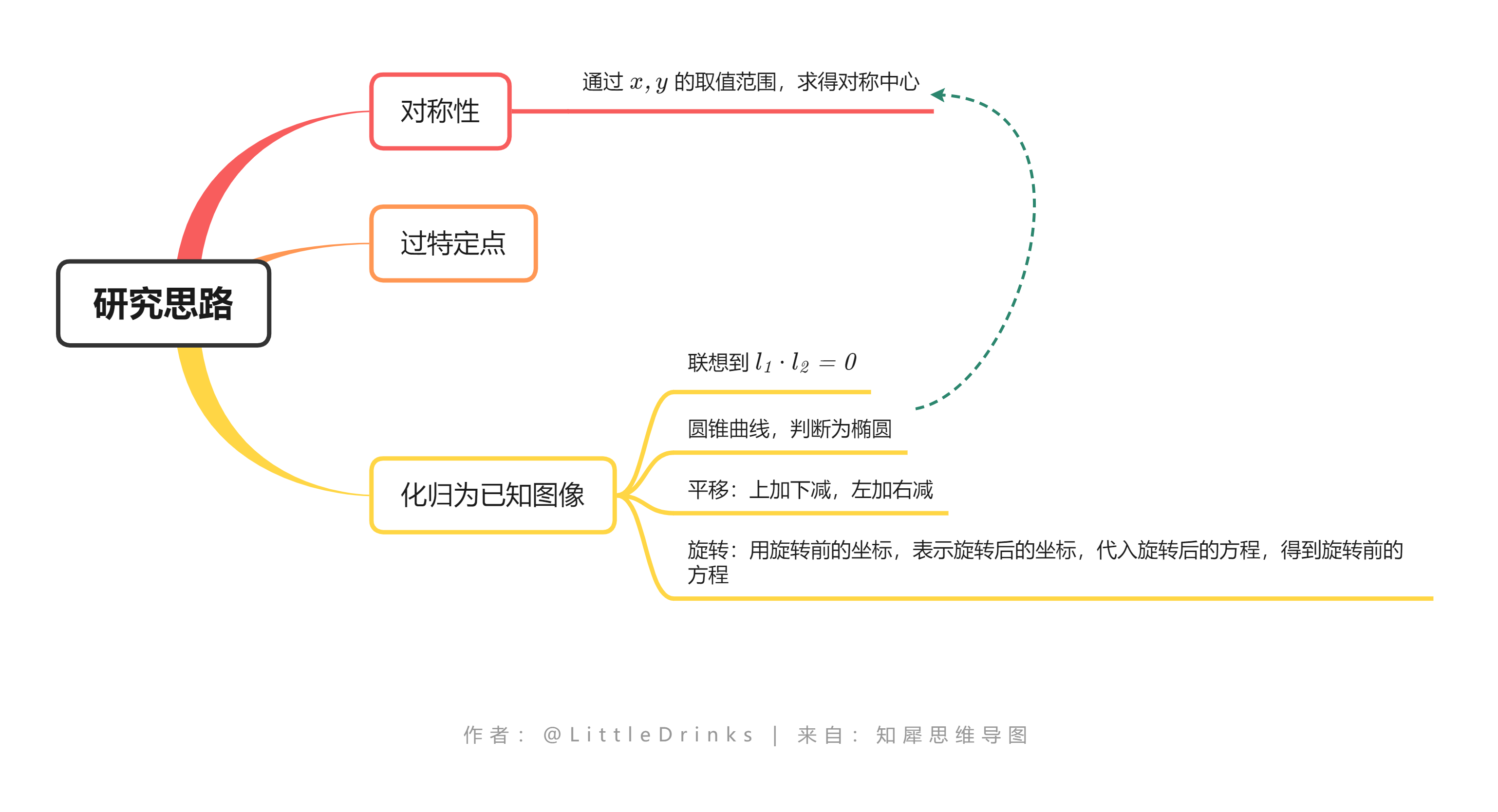
总结
由上文对两个方程的探究,可以总结出方程图像研究的具体条目:
- 是否过特定点
- 对称性
- 看到偶次项,代入 \(P(-x,y)\) 等研究其对于坐标轴、原点的对称性
- 看到形式上很对称的方程,\(x,y\) 完全可以互换,可以考虑 \(y=x\)
- 有关于某个特定点的对称性(如椭圆的对称中心),可以通过 \(x,y\) 取值范围的中心求出这一对称中心
- 具有对称性的图像,使用极坐标进行研究会比较简便
- 化归为已知方程
- 类比圆进行配方,可求最值
- 判断 \(x,y\) 是否可以取遍一切实数判断是否为有限的封闭图形
- 二次曲线 \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) 是圆锥曲线
- 平移:上加下减,左加右减
- 旋转:用旋转前的坐标,表示旋转后的坐标,代入旋转后的方程,得到旋转前的方程
- 如果方程两侧形式一致,可以考虑抽象为同一个函数 \(f(a)\),进而研究 \(f(a)\)
上文对思路的罗列可能略显凌乱,接下来将通过研究方程 \(x^4+y^4=1\) 实践总结出的策略。
Q3:\(x^4+y^4=1\)
- 显然过点 \((\pm1,0),(0,\pm1)\)
- 对称性
- 都是偶次项,代入 \(P(-x,y)\) 等易得方程图像关于原点、坐标轴对称
- 形式对称,代入 \(Q(y,x)\) 符合,说明其关于直线 \(y=x\) 对称
- 无特殊对称中心
- 使用极坐标,设 \(\begin{cases}x=\rho\cos\theta\\ y=\rho\sin\theta\end{cases}\),代入得到 \(\rho^4(\cos^4\theta+\sin^4\theta)=1\),使用降次公式化简得到 \(\rho^4=\displaystyle\frac{4}{3+\cos4\theta}\),从形式上看类似于一个圆,对比单位圆 \(\rho=1\) 可以形象地知道:原方程图像比单位圆胖出一圈
- 化归为已知图像
- 类比圆,此处已经完成配方,易得当 \(x=0\) 时 \(y_{max}=1,y_{min}=-1\)。
- 取其第一象限研究,移项得 \(y=\sqrt[4]{1-x^4}\),随着 \(x\) 的增大 \(y\) 减小,并且 \(\begin{cases}-1\leq x\leq1\\ -1\leq y\leq 1\end{cases}\)
- 四次曲线,不是圆锥曲线
- 不必考虑平移或旋转
- 设原方程等价于 \(x^4+m=-y^4-m\),计算得 \(m=-\displaystyle\frac12\),于是可以抽象出函数 \(f(a)=a^4-\displaystyle\frac12\),曲线上的点 \((x,y)\) 满足 \(f(x)=-f(y)\)。由图像的对称性,仅研究第一象限内 \(y>x\) 的部分,同样可以得到:该部分图像在 \([0,\displaystyle\sqrt[4]\frac12]\) 上严格减,端点为 \((0,1),\ (\displaystyle\sqrt[4]\frac12,\displaystyle\sqrt[4]\frac12)\)
综合上述研究,容易画出原函数的图像:
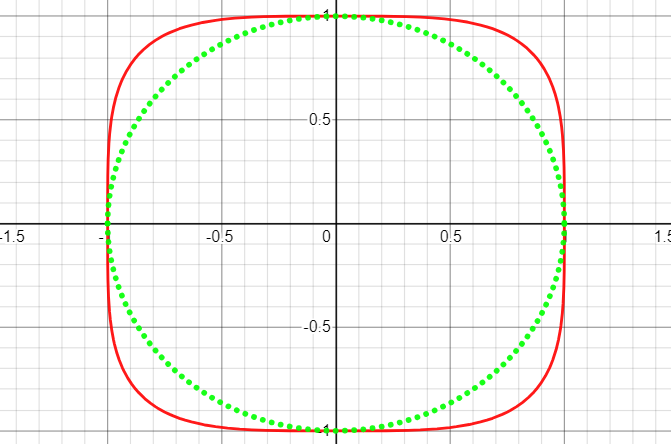
结语
通过对三个方程的研究,本文研究了方程图像绘制的具体研究条目,为研究抽象方程提供了路径。
受制于研究的方程数量,本文的总结可能有所欠缺,有待进一步补充。
参考资料
(均已在使用处以链接形式标出)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号