分块

分块是一种码量较小，复杂度相对优秀的算法。

可以参考 OI wiki上对分块的介绍。

例题引入：P3870 [TJOI2009] 开关

这道题用来介绍分块的基本操作。

首先题意非常明确，需要维护区间求和、区间取反两种操作，暴力修改查询的话，单次需要 \(O(n)\)。

我们可以将 \(sz\) 个连续的灯划为一个块。

为什么要分块呢？

设 \(cnt\) 表示某时刻亮着的灯的数量，即答案。对所有灯进行一次取反操作，此时的答案可以很快维护出来，即 \(cnt\leftarrow n-cnt\)，而维护的过程并没有做单点修改，打个懒标记记录一下即可。

推广一下，对于一段固定的区间 \([L,R]\)，我们可以记录下这段区间的大小 \(k\) 和答案 \(cnt_i\)，在对整块操作时，令 \(cnt_i\leftarrow k-cnt_i\)，再打上懒标记，在 \(O(1)\) 的时间内将答案维护出来，节约时间。也就是说，整块相较一个一个单点修改，有较优的方式维护，而剩下的散点则可以用相对暴力的方式维护。 通过分块，我们就可以利用这一较优的维护方式。

但这种做法是有问题的。首先，这段区间 \([L,R]\) 的长度不能太小，这样才能起到优化时间的作用，否则相当于一个一个单点修改。可是，一旦区间长度增大，那么单次修改【整个】区间的可能性就随之降低。也就是说，整块长度越大，优化时间越多，但优化到的概率却越低。

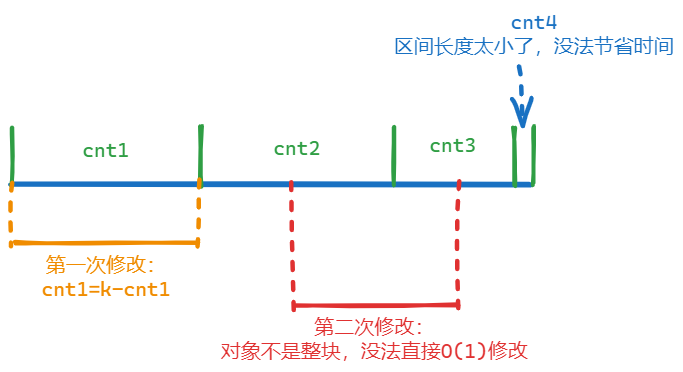
为了在【优化时间】和【优化概率】之间达到平衡，我们设单个块的大小为 \(sz\)，共有 \(\displaystyle k=\lceil\frac{n}{sz}\rceil\) 个块，接下来，我们需要通过计算确定具体的取值。

考虑单次修改的时间复杂度。我们最多对 \(k\) 个块进行整块的操作，而整块修改单次 \(O(1)\)；最多对 \(2\times sz\) 个单点下传懒标记并进行暴力修改，时间复杂度 \(O(sz)\)。单次修改总时间复杂度 \(O(k+sz)\)。查询时同理。

设修改次数为 \(n\)，于是总的时间复杂度为：\(\displaystyle O(n\times sz+\frac{n^2}{sz})\)，当 \(\displaystyle n\times sz=\frac{n^2}{sz}\Rightarrow n=\sqrt n\) 时有最小时间复杂度 \(O(n\sqrt n)\)。这个复杂度相当优秀，加上分块常数较小，可以和 \(O(n\log^2 n)\) 甚至 \(O(n\log n)\) 的算法媲美。

总结一下分块的思路：

• 针对题目中要求的操作，找到一种节约时间的整块维护方式；
• 计算复杂度，推导 \(sz\) 的取值，在【优化时间】和【优化概率】之间达到平衡；
• 对单点和整块分开处理。

具体实现见代码，主要关注【如何分块】、【如何在操作时区分单点和整块】。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXN=1e5+5, MAXK=355;
int n, m, k, L[MAXK], R[MAXK], belong[MAXN];
int cnt[MAXK], tag[MAXK], status[MAXN];

void modify(int a, int b)
{
	// a、b在一个块内，直接暴力修改
	if (belong[a] == belong[b]) {
		for (int i = a; i <= b; ++i) {
			status[i]^=1, cnt[belong[i]]+=(status[i]^tag[belong[i]]?1:-1);
		}
		return;
	}
	
	// a往后不满一个块
	int l=L[belong[a]], r=R[belong[a]];
	while ( (l<a) && (a<=r) ) {
		status[a]^=1, cnt[belong[a]]+=(status[a]^tag[belong[a]]?1:-1), ++a;
	}
	
	// b往前不满一个块
	l=L[belong[b]], r=R[belong[b]];
	while ( (l<=b) && (b<r) ) {
		status[b]^=1, cnt[belong[b]]+=(status[b]^tag[belong[b]]?1:-1), --b;
	}
	
	// 整块处理
	for (int i = belong[a]; i <= belong[b]; ++i) {
		tag[i]^=1, cnt[i]=R[i]-L[i]+1-cnt[i];
	}
}

int query(int a, int b)
{
	int res=0;
	
	// a、b在一个块内，直接暴力修改
	if (belong[a] == belong[b]) {
		for (int i = a; i <= b; ++i) {
			res += status[i]^tag[belong[i]];
		}
		return res;
	}
	
	// a往后不满一个块
	int l=L[belong[a]], r=R[belong[a]];
	while ( (l<a) && (a<=r) ) {
		res+=status[a]^tag[belong[a]], ++a;
	}
	
	// b往前不满一个块
	l=L[belong[b]], r=R[belong[b]];
	while ( (l<=b) && (b<r) ) {
		res += status[b]^tag[belong[b]], --b;
	}
	
	// 整块处理
	for (int i = belong[a]; i <= belong[b]; ++i) {
		res += cnt[i];
	}
	
	return res;
}

int main()
{
	cin.tie(nullptr) -> sync_with_stdio(false);

	// I.N.
	cin >> n >> m;
	
	// init
	k = sqrt(n);
	for (int i = 1; i <= k; ++i) {
		L[i]=(i-1)*k+1, R[i]=i*k;
		for (int j = L[i]; j <= R[i]; ++j) { belong[j]=i; }
	}
	if (R[k] < n) {
		++k, L[k]=R[k-1]+1, R[k]=n;
		for (int j = L[k]; j <= R[k]; ++j) { belong[j]=k; }
	}
	
	//
	while (m--) {
		int c, a, b;
		cin >> c >> a >> b;
		if (c == 0) {
			modify(a, b);
		} else {
			cout << query(a, b) << endl;
		}
	}
	
	// E.D.
	return 0;
}

题单

题目	备注
P3870 [TJOI2009] 开关	例题，用于讲解分块操作
U332582 树上距离	模拟赛题目，分块思想的应用
P3203 [HNOI2010] 弹飞绵羊	用分块压缩区间信息
P4168 [Violet] 蒲公英	蓝书的题，强制在线的区间众数，用分块处理区间不可加问题
Acwing252 磁力块	蓝书的题，一个分块后的小技巧
P2617 Dynamic Rankings	动态第 k 大问题的分块解法
Anton and Permutation	动态逆序对的分块做法

CF342E Xenia and Tree

常规的暴力做法是 \(O(1)\) 做单点修改，\(O(n)\) 做单次 bfs 查询。或者 \(O(n)\) 把全局的距离全部更新，\(O(1)\) 做单点查询。接下来自然的一个想法，就是牺牲一点修改或者查询的时间，使两者达到平衡。

本题的正解是对操作序列分块，将一些修改操作堆积在一起，一次性做完。

具体而言，设现在每个节点到其最近红色节点的距离为 \(dis_i\) ，块长为 \(k\)，队列当前为空。

每当遇到一个修改操作，直接将其加入队列。期间如果遇到对节点 \(u\) 的查询，利用 【st 表+欧拉序】在 \(O(1)\) 时间内求出队列中每个节点到 \(u\) 的距离，再与 \(dis_u\) 取较小值即可，时间复杂度 \(O(qk)\)。

当队列中堆积的修改操作大于 \(k\) 后，用 bfs 进行一次全局修改。这种操作共进行 \(\displaystyle\frac{q}{k}\) 次，时间复杂度 \(\displaystyle O(\frac{qn}{k})\)。

总时间复杂度 \(\displaystyle O(qk+\frac{qn}{k})\)，假设 \(q,n\) 同构，当 \(k=\sqrt n\) 时有时间复杂度最小值 \(O(n\sqrt n)\)。

注：倍增求两点距离的话，目前的数据是 80 分。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;
typedef pair<int,int> pii;

const int N=1e5+5;
int n, m;
vector<int> nd;
vector<int> G[N];

template<typename T>
struct ST {
    int n, I;
    vector<int> Log;
    vector<vector<T>> st;
    ST() {}
    ST(const vector<T> &a): n(a.size()), Log(vector<int>(n+1)) {
        for (int i = 2; i <= n; ++i) {
            I = Log[i] = Log[i/2] + 1;
        }
        st.assign(I+1, vector<T>(n));
        copy(a.begin(), a.end(), st[0].begin());
        for (int i = 1; i <= I; ++i) {
            for (int j = 0; j+(1<<(i-1)) < n; ++j) {
                st[i][j] = min(st[i-1][j], st[i-1][j+(1<<(i-1))]);
            }
        }
    }
    T query(int l, int r) {
        assert(l <= r);
        int s = Log[r-l+1];
        return min(st[s][l], st[s][r-(1<<s)+1]);
    }
};

int dep[N], first[N];
vector<pii> eular;
void dfs(int u, int fa)
{
    first[u] = eular.size();
    dep[u] = dep[fa] + 1;
    eular.push_back( { dep[u], u } );
    for (int v: G[u]) {
        if (v != fa) {
            dfs(v, u);
            eular.push_back( { dep[u], u } );
        }
    }
}
ST<pii> st;
int LCA(int u, int v)
{
    u = first[u];
    v = first[v];
    if (u > v) { swap(u, v); }
    return st.query(u, v).second;
}

int d[N];
bool vis[N];
void bfs()
{
    queue<int> q;
    memset(vis, 0, sizeof(vis));
    for (int x: nd) { q.push(x); d[x]=0; }
    nd.clear();
    while (!q.empty()) {
        int u = q.front(); q.pop();
        if (vis[u]) { continue; }
        vis[u] = true;
        for (int v: G[u]) {
            if (!vis[v]) { d[v]=min(d[v], d[u]+1); q.push(v); }
        }
    }
}

int main()
{
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i < n; ++i) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    int k = sqrt(m);
    memset(d, 0x3f, sizeof(d));
    dfs(1, 0);
    st=ST<pii>(eular);
    nd.push_back(1);
    while (m--) {
        int t, v;
        cin >> t >> v;
        if (t == 1) {
            nd.push_back(v);
            if ((int)nd.size() > k) { bfs(); }
        } else {
            int ans = d[v];
            for (int x: nd) {
                int lca = LCA(x, v);
                ans = min(ans, dep[x]+dep[v]-2*dep[lca]);
            }
            cout << ans << "\n";
        }
    }
}

P3203 [HNOI2010] 弹飞绵羊

这题其实把思路讲出来就很简单了，但初看真的想不到。

首先最原始的做法就是暴力，一个一个跳，单次查询复杂度 \(O(ans)\)。

但这很明显太慢了，优化思路是，如果没有修改操作，弹飞的路径是固定的，完全可以将一段弹力装置放在一起处理，或者说，把某一段弹力装置压缩变成一个超级弹力装置。

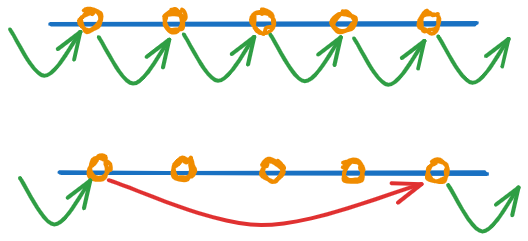
在没有修改的情况下，我们自然而然地就会想到，把所有弹力装置从头到尾压缩在一起。但加上了修改，情况就不一样了。重新计算超级弹力装置的时间是 \(O(sz)\)，其中 \(sz\) 表示这个超级弹力装置压缩了几个弹力装置。如果把所有弹簧压缩在一起，这个修改成本是非常高的。

整块有利于查询操作，单点有利于修改操作。于是考虑分块。

设块的大小为 \(sz\)，共有 \(k=\displaystyle\frac{n}{sz}\) 个块。

查询时，至多经历 \(k\) 个块，单次复杂度 \(O(1)\)，总时间复杂度 \(O(k)\)。

修改时，重新计算这个块，算出在不同位置进入这个块所对应的弹出位置，单次复杂度 \(O(sz)\)，一次只修改一个弹力值，同时重新计算它所在的块，总复杂度 \(O(sz)\)。

共 \(m\) 次操作，总时间复杂度 \(\displaystyle O(m(sz+\frac{n}{sz}))\)，当 \(sz=\sqrt n\) 时有复杂度最小值 \(O(m\sqrt n)\)。

最后，本题和 CF13E 重复，双倍经验。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXN=2e5+5, MAXK=450;
int n, m, k, a[MAXN], L[MAXK], R[MAXK], belong[MAXN], arr[MAXN], cnt[MAXN];

void update(int block, int ith)
{
	arr[ith] = (ith+a[ith]>R[block]? ith: arr[ith+a[ith]]);
	cnt[ith] = (ith+a[ith]>R[block]? 0: cnt[ith+a[ith]]+1);
}

void init()
{
	k = sqrt(n);
	for (int i = 1; i <= k; ++i) {
		L[i]=(i-1)*k+1, R[i]=i*k;
	}
	if (R[k] < n) {
		++k, L[k]=R[k-1]+1, R[k]=n;
	}
	for (int i = k; i; --i) {
		for (int j = R[i]; j >= L[i]; --j) {
			belong[j]=i;
			update(i, j);
		}
	}
	
}

void modify(int x, int y)
{
	a[x] = y;
	for (int i = x; i >= L[belong[x]]; --i) {
		update(belong[x], i);
	}
}

int query(int x)
{
	int res=0;
	while (x <= n) {
		res+=cnt[x], x=arr[x];
		x=x+a[x], ++res;
	}
	return res;
}

int main()
{
	// cin.tie(nullptr) -> sync_with_stdio(false);

	// I.N.
	cin >> n;
	for (int i = 1; i <= n; ++i) { scanf("%d", &a[i]); }
	
	// 预处理分块信息
	init();
	
	// O.P.
	scanf("%d", &m);
	while (m--) {
		int op, x, y;
		scanf("%d%d", &op, &x), ++x;
		if (op == 1) {
			printf("%d\n", query(x));
		} else {
			scanf("%d", &y);
			modify(x, y);
		}
	}
	
	// E.D.
	return 0;
}

P4168 [Violet] 蒲公英

强制在线的区间众数问题。

首先会有一个显然的暴力 \(O(mn)\) 做法，枚举 \([L,R]\)，开个桶记录一下就行了。

由于本题强制在线，\(m\) 这个维度是不可能优化掉的，只能从 \(n\) 下手。显然，不加任何预处理的情况下，直接扫一遍的 \(O(n)\) 解法是获取区间众数的最优做法了。想要优化，就要通过预处理一些量，在多次询问间压缩掉多余的扫描。

提到预处理众数，可能的第一反应就是对每种蒲公英预处理前缀和，快速求出某段区间内该种蒲公英的数量，进而优化枚举的时间。

这种思路有两个问题。一是，预处理每种蒲公英的前缀和是 \(O(n^2)\) 的运算量，会爆时间和空间。二是，单次询问需要拿到区间内所有出现过的数字，这依然不好维护。

这里参考蓝书上的一种做法，用分块解决这两个问题。

首先，想要求出某段区间 \([L,R]\) 内数字 \(x\) 出现的次数，不一定要用前缀和，我们可以牺牲一点查询的时间来换取较为快捷的预处理。具体而言，我们可以对每种蒲公英开一个 vector，记作 \(cnt[a_i]\)，记录下每种蒲公英的出现位置。每次询问出现的次数时，做两次二分即可，看有多少下标落在 \([L,R]\) 这个区间内，就是答案。预处理所有蒲公英的时间是 \(O(n)\)，单次查询 \(O(\log n)\)，在这里很合适。

然后，【不知道这个区间内出现了哪些数字】的问题其实可以换一个角度看，只需要把对答案计算没用的数字撇去就可以了。假设我们已经知道了区间 \([L,R]\) 的众数，在询问区间 \([L-1,R]\) 的时候会有【两种可能】，要么答案就是 \([L,R]\) 的众数，要么答案是 \(a_{L-1}\)，换句话说，除了区间 \([L,R]\) 的答案和 \(a_{L-1}\)，剩下所有数字都是没用的，根本不用看。

引用分块的概念，这里限制时间复杂度的，是散块的大小。设块的大小为 \(sz\)，一共有 \(k\) 个块，通过分块，我们可以将散块的大小限制在 \(2sz\) 以内，散块单次查询复杂度 \(O(sz\log n)\)。

对整块而言，我们需要预处理出第 \(l\) 到第 \(r\) 个整块的答案，记作 \(ans_{[l,r]}\)。从块左端点开始向右暴力扫描，开个桶记录出现次数，预处理时间复杂度 \(O(kn)\)，查询时间复杂度 \(O(1)\)。

最后求答案的时候，只需要看【整块的众数】和【散块中出现的次数】就可以了。总的来说，预处理时间复杂度 \(\displaystyle O(kn)=O(\frac{n^2}{sz})\)，查询时间复杂度 \(O(m\times sz\log n)\)，总时间复杂度 \(\displaystyle O(\frac{n^2}{sz}+m\times sz\log n)\)，假设 \(n,m\) 同构，当左右两部分相等时，即 \(\displaystyle sz=\sqrt{\frac{n}{\log n}}\) 时，有时间复杂度最小值 \(O(n\sqrt{n\log n})\)。

整理一下代码的思路。

1. 分块，块的大小 \(sz=n\sqrt{n\log n}\)；
2. 枚举块作为左端点，开个桶向右暴力扫描，预处理 \(ans_{[l,r]}\)，表示第 \(l\) 到 \(r\) 个块的答案；
3. 预处理 \(cnt[a_i]\)，表示第 \(a[i]\) 种蒲公英出现的下标，开个 vector 往里丢就行了；
4. 对于每次询问，对于散块中出现过的数字，可以通过在 \(cnt[a[i]]\) 内二分快速求出出现次数，与整块的答案合并，就是询问的答案。

AC 代码提交记录

（这份代码里面 \(sz\) 表示了块的数量，可能跟上文所说不太一样，比较抽象……）

#include <bits/stdc++.h>

using namespace std;

const int MAXN=4e4+5, MAXK=805;
int n, m, a[MAXN], b[MAXN], a_to_tp[MAXN], tot;
int k, sz, L[MAXK], R[MAXK], belong[MAXN];
int ans[MAXK][MAXK][2], ht[MAXN];
vector <int> cnt[MAXN];

inline int read()
{
    int ret=0;
    int f=1;
    char c=getchar();
    while(c<'0' || c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0' && c<='9'){
        ret=ret*10+c-'0';
        c=getchar();
    }
    return ret*f;
}

inline int get_frequency(int num, int l_aid, int r_aid)
{
	// 查看在[l_aid,r_aid]之间 num 出现了多少次
	int rid=upper_bound(
		cnt[num].begin(),cnt[num].end(),r_aid)-cnt[num].begin();
	int lid=lower_bound(
		cnt[num].begin(),cnt[num].end(),l_aid)-cnt[num].begin();
	return rid-lid;
}

inline void update(int num, int fqc, int &tp, int &tpcnt)
{
	if ( (fqc>tpcnt) || (fqc==tpcnt && num<tp)) {
		tp=num, tpcnt=fqc;
	}
}

inline void init()
{
	// 离散化
	sort(b+1, b+n+1), tot=unique(b+1, b+n+1)-(b+1);
	for (int i = 1; i <= n; ++i) {
		a_to_tp[i] = lower_bound(b+1, b+tot+1, a[i])-(b);
	}
	
	// 分块信息
	sz=sqrt(n*log(n)), sz=(sz==0? 1: sz), k=n/sz;
	for (int i = 1; i <= sz; ++i) {
		L[i]=(i-1)*k+1, R[i]=i*k;
	}
	if (R[sz] < n) {
		++k, L[sz]=R[sz-1]+1, R[sz]=n;
	}
	for (int i = 1; i <= sz; ++i) {
		for (int j = L[i]; j <= R[i]; ++j) {
			belong[j]=i;
			cnt[a_to_tp[j]].push_back(j);  // 预处理 cnt[a[i]]，表示 a[i]种蒲公英出现的下标
		}
	}
	
	// 预处理 ans[l][r]
	// 枚举左端点，然后枚举右端点进行操作
	// 对于 a[i]，它属于第 belong[a[i]]个块，用二分看它在[i,belong[a[i]]]这些块中出现了多少次
	// 记下 a[i]的答案，不清空、只更新
	// 直到这一个块扫完，将答案填入 ans[l][r]
	for (int i = 1; i <= sz; ++i) {
		int tp=0, tpcnt=0;  // tp : type
		memset(ht, 0, sizeof(ht));
		for (int j = i; j <= sz; ++j) {
			for (int z = L[j]; z <= R[j]; ++z) {  // 对一个块内进行扫描，每次处理 a[z]的答案
				update(a_to_tp[z], ++ht[a_to_tp[z]], tp, tpcnt);
			}
			ans[i][j][0]=tp, ans[i][j][1]=tpcnt;
		}
	}
}

inline int query(int l, int r)
{
	int i=l, j=r, tp=0, tpcnt=0;
	
	// 求散块的答案
	while ( (L[belong[i]]<i) && (i<=R[belong[i]]) ) {
		// 收缩左边界，对于 a[i]，看它在左侧散块中出现了多少次
		update(a_to_tp[i], get_frequency(a_to_tp[i], l, r), tp, tpcnt), ++i;
	}
	while ( (L[belong[j]]<=j) && (j<R[belong[j]]) ) {
		// 同上收缩右边界
		update(a_to_tp[j], get_frequency(a_to_tp[j], l, r), tp, tpcnt); --j;
	}
	
	// 将整块的答案合并
	if (tpcnt == ans[ belong[i] ][ belong[j] ][1]) {  // 频次相同，取编号较小
		tp = min(tp, ans[ belong[i] ][ belong[j] ][0]);
	} else if (tpcnt < ans[ belong[i] ][ belong[j] ][1]) {  // 整块答案频次大，否则就不更新
		tp = ans[ belong[i] ][ belong[j] ][0];
	}
	
	// 返回答案
	return tp;
}

int main()
{
	cin.tie(nullptr) -> sync_with_stdio(false);
	n=read(), m=read();
	for (int i = 1; i <= n; ++i) {
		a[i]=read(), b[i]=a[i];
	}
	
	// 预处理：分块、块的答案
	init();
	
	// Q.E.
	int x=0, l, r;
	while (m--) {
		// 输入询问 and 解密
		// cin >> l >> r;
		// scanf("%d%d", &l, &r);
		l=read(), r=read();
		l=(l+x-1)%n+1, r=(r+x-1)%n+1;
		if (l > r) { swap(l,r); }
		
		// 处理询问
		x = b[query(l,r)];
		
		printf("%d\n", x);
	}
	
	// E.D.
	return 0;
}

Acwing252 磁力块

每一块磁石都可以将在范围内、并且质量不大于它的磁石吸到身边。视磁石质量和磁力不同，可能有的磁石磁力大但是质量小，吸引不了质量大的磁石，反之亦然。因此，防止多维度的最优解被忽略，在极限情况下每块磁石都要被考虑一次，复杂度 \(O(n)\)。吸到后的磁石就不必再次考虑，可以使用队列维护，开始时，将磁石 \(L\) 放入队列。对于剩下的磁石，需要找到一种较优复杂度的做法，快速把一块磁石能吸引的全部加入队列之中。

于是问题转化为了二维偏序问题。

首先，第一想法肯定是通过排序消除一个维度，比如选择根据距离进行排序。此时想要判断磁力的相对关系，只需要一次二分即可。但此时第二个维度质量就变得非常无序，只能暴力扫描，复杂度 \(O(n)\)，爆了。

为了平衡两个维度的查询时间，我们可以考虑分块。将剩下的磁石按照距离排序，排完序后分块，块内按照质量排序。每次去除队列开头的石头 \(x\)，设其在第 \(belong[x]\) 块中。

若磁石在 \(belong[x]\) 左侧的块中，距离符合条件，块内找质量满足条件的磁石即可。该步可以维护一个指针 \(l\_id\)，表示磁石最左侧还未被取走的磁石，再维护一个 \(taken[]\)，如果符合条件就右移指针，然后在 \(taken[]\) 中标记。

若磁石在 \(belong[x]\) 右侧的块中，距离不符合条件，不用考虑。在第 \(belong[x]\) 块内，直接遍历每一个磁石看是否符合条件。

预处理时先按照距离排序，再在块内按照质量排序。每次用新的磁石进行吸引时，首先需要二分找到块的位置，然后每个块内从左往右将符合条件的磁石加入队列中。块长设置为 \(\sqrt{n}\)，时间复杂度够用。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXN=250005, MAXK=505;
long long x_0, y_0, ans, dis_max[MAXK];
int n, k, sz, L[MAXK], R[MAXK], belong[MAXN], l_ms_id[MAXK];
queue <long long> q;
bool taken[MAXN];

struct magnet_stone {
	long long dis, m, p, r;
} ms[MAXN];

long long dis2(long long x, long long y)
{
	return (x-x_0)*(x-x_0)+(y-y_0)*(y-y_0);
}

bool cmp_dis(magnet_stone a, magnet_stone b)
{
	return a.dis < b.dis;
}

bool cmp_m(magnet_stone a, magnet_stone b)
{
	return a.m < b.m;
}

void init()
{
	// 分块信息
	k=sqrt(n), sz=n/k;
	for (int i = 1; i <= sz; ++i) {
		L[i]=(i-1)*k+1, R[i]=i*k;
	}
	if (R[sz] < n) {
		++sz, L[sz]=R[sz-1]+1, R[sz]=n;
	}
	for (int i = 1; i <= sz; ++i) {
		l_ms_id[i] = L[i];
		for (int j = L[i]; j <= R[i]; ++j) {
			belong[j] = i;
		}
	}
	
	// 按照距离对 ms[]进行排序
	sort(ms+1, ms+n+1, cmp_dis);
	
	// 块内按照质量排序
	for (int i = 1; i <= sz; ++i) {
		dis_max[i] = ms[R[i]].dis;  // 块内距离最大值，用于二分
		sort(ms+L[i], ms+R[i]+1, cmp_m);
	}
}

void attract(int curr)
{
	// 先按照距离，找到最大值严格大于 ms[curr].r*ms[curr].r 的块 x
	int x=upper_bound(dis_max+1, dis_max+sz+1, ms[curr].r*ms[curr].r)-(dis_max);
	// x = (x==0? 1: x);
	
	// 在块 x 的左侧，距离都符合条件，直接看质量
	for (int i = 1; i < x; ++i) {
		while (l_ms_id[i] <= R[i]) {
			if (taken[l_ms_id[i]]) {  // 已经吸上来了，跳过
				++l_ms_id[i];
			} else if (ms[l_ms_id[i]].m <= ms[curr].p) {  // 符合条件，吸上来
				++ans, taken[l_ms_id[i]]=true, q.push(l_ms_id[i]), ++l_ms_id[i];
			} else {  // 质量不符合条件，向右质量递增，也不可能符合条件，跳出循环
				break;
			}
		}
	}
	
	// 如果 x 超出了块的范围，直接跳出
	if (x > sz) { return; }
	
	// 对于块 x，扫描其中每一个磁石，判断是否符合条件
	for (int i = l_ms_id[x]; i <= R[x]; ++i) {
		if (taken[i]) {  // 已经吸上来了，跳过
			continue;
		} else if ( (ms[i].m<=ms[curr].p) && (ms[i].dis<=ms[curr].r*ms[curr].r) ) {  // 符合条件，吸上来
			++ans, taken[i]=true, q.push(i);
		}
	}
}

int main()
{
	cin.tie(nullptr) -> sync_with_stdio(false);

	// I.N.
	cin >> x_0 >> y_0 >> ms[0].p >> ms[0].r >> n; q.push(0);
	for (int i = 1; i <= n; ++i) {
		long long x,y; cin>>x>>y; ms[i].dis=dis2(x,y);  // 输入距离
		cin >> ms[i].m >> ms[i].p >> ms[i].r;           // 输入其他量
	}
	
	// 预处理分块信息
	init();
	
	// 类 bfs 吸引磁石
	while (!q.empty()) {
		int curr=q.front(); q.pop();
		attract(curr);
	}
	
	// E.D.
	cout << ans << endl;
	return 0;
}

P2617 Dynamic Rankings

这里介绍一下动态第 \(k\) 大问题的分块做法。

和线段树一样，分块的特点，是易于处理区间可加性问题，但在很多时候，在有限时空限制内无法通过区间相加直接维护出想要的量，此时可以转换思路，间接维护。

除此之外，分块还可以在分完的块内进行排序操作，以维护有序性，便于调用。

在这里，将两个想法相结合，就可以得到本题的正解。

首先，动态第 \(k\) 大问题显然不能转化为区间可加性问题，不用想着开个桶死磕什么的（好像有对值域分块的做法，但我不会 qwq）。我们对序列分块，将块内排序后二分答案 \(x\)，每次验证答案时利用块内有序性，快速求出比 \(x\) 小的元素个数，把多个块的答案相加，就能得到 \(x\) 的排序。

块长取 \(\sqrt n\) 即可，不开 O2 也可以在 2.8 秒左右通过最大的测试点。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXN=1e5+5, MAXK=355;
int n, q, a[MAXN];
vector <int> arr(MAXN);
int k, sz, L[MAXK], R[MAXK], belong[MAXN];

void init()
{
	// 分块信息
	k=sqrt(n), sz=n/k;
	for (int i = 1; i <= k; ++i) {
		L[i]=(i-1)*sz+1, R[i]=i*sz;
	}
	if (R[k] < n) {
		++k, L[k]=R[k-1]+1, R[k]=n;
	}
	for (int i = 1; i <= k; ++i) {
		for (int j = L[i]; j <= R[i]; ++j) {
			belong[j] = i;
		}
		sort(arr.begin()+L[i], arr.begin()+R[i]+1);
	}
}

void modify(int x, int y)
{
	arr.erase(
		lower_bound(arr.begin()+L[belong[x]], arr.begin()+R[belong[x]], a[x])
	);
	arr.insert(
		upper_bound(arr.begin()+L[belong[x]], arr.begin()+R[belong[x]], y), y
	);
	a[x] = y;
}

int get_lower_cnt(int l, int r, int num)
{
	int cnt=0;
	if (belong[l] == belong[r]) {
		for (int i = l; i <= r; ++i) {
			cnt += (a[i]<num);
		}
		return cnt;
	}
	while ( (L[belong[l]]<l) && (l<=R[belong[l]]) ) { cnt+=(a[l]<num), ++l; }
	while ( (L[belong[r]]<=r) && (r<R[belong[r]]) ) { cnt+=(a[r]<num), --r; }
	for (int i = belong[l]; i <= belong[r]; ++i) {
		cnt += lower_bound(arr.begin()+L[i], arr.begin()+R[i]+1, num)-(arr.begin()+L[i]);
	}
	return cnt;
}

int query(int x, int y, int k)
{
	int l=0, r=1e9+5, mid=(l+r)>>1, cnt;
	while (l != r-1) {
		mid=(l+r)>>1, cnt=get_lower_cnt(x, y, mid);
		if (cnt > k-1) {
			r = mid;
		} else {
			l = mid;
		}
	}
	return l;
}

int main()
{
	cin.tie(nullptr) -> sync_with_stdio(false);

	// I.N.
	cin >> n >> q;
	for (int i = 1; i <= n; ++i) { cin>>a[i]; arr[i]=a[i]; }
	init();
	
	// O.P.
	while (q--) {
		char op;
		int x, y, k;
		cin >> op >> x >> y;
		if (op == 'C') {
			modify(x, y);
		} else {
			cin >> k;
			cout << query(x, y, k) << endl;
		}
	}
	
	// E.D.
	return 0;
}

Anton and Permutation

这里介绍一下动态逆序对的分块做法。

设块的大小为 \(k\)，则块的数量为 \(\displaystyle\frac{n}{k}\)。设 query(l+1,r-1,v) 表示区间 \([l+1,r-1]\) 中严格小于 \(v\) 的数的个数。

接下来我们讨论交换 \(n_1\)、\(n_2\) 后对答案的贡献：

为了方便表述，这里设 \([l+1,r-1]\) 中的任意一个数是 \(a\)。

当 \(n_1\) 往后移动时，若移动前 \((n_1,a)\) 是逆序对，则该逆序对被消除，即 ans += -query(l+1,r-1,n_1)；若移动前 \((n_1,a)\) 不是逆序对，则 \((a,n_1)\) 是逆序对，即 ans += (r-l-1)-query(l+1,r-1,n_1)。

同理，当 \(n_2\) 往前移动时，ans += query(l+1,r-1,n_2)，ans += -(r-l-1)+query(l+1,r-1,n_2)。

最后，若 \((n_1,n_2)\) 是一个逆序对，则交换后被消除，--ans，否则 ++ans。

具体实现时，块内排序做二分即可。query() 的时间复杂度 \(\displaystyle O(k + \frac{n\log{k}}{k})\)；update() 的时间复杂度 \(O(k)\)；modify() 的时间复杂度 \(\displaystyle O( n \times (k + \frac{n\log n}{k}) )\)。块长取 \(k=\sqrt{n\log n}\)。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXN=2e5+5, MAXK=2000;
int n, a[MAXN], b[MAXN], q;
long long ans;
int k, sz, L[MAXK], R[MAXK], belong[MAXN];
int num_to_aid[MAXN], num_to_bid[MAXN];

inline int read()
{
    int ret=0;
    int f=1;
    char c=getchar();
    while(c<'0' || c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0' && c<='9'){
        ret=ret*10+c-'0';
        c=getchar();
    }
    return ret*f;
}

inline void init()
{
	// 初始化原序列
	for (int i = 1; i <= n; ++i) { a[i]=b[i]=i, num_to_aid[i]=num_to_bid[i]=i; }
	
	// 分块
	k=sqrt(n*log2(n)), k=(k==0? 1: k);
	// k = sqrt(n);
	sz = n/k;
	for (int i = 1; i <= sz; ++i) {
		L[i]=(i-1)*k+1, R[i]=i*k;
	}
	if (R[sz] < n) {
		++sz, L[sz]=R[sz-1]+1, R[sz]=n;
	}
	for (int i = 1; i <= sz; ++i) {
		for (int j = L[i]; j <= R[i]; ++j) {
			belong[j] = i;
		}
	}
}

inline long long query(int l, int r, int v)
{
	// 求[l,r]区间内比 v 小的数的个数
	if (l>r) { return 0; }
	long long res=0;
	if (belong[l] == belong[r]) {
		for (int i = l; i <= r; ++i) {
			res += (a[i]<v);
		}
		return res;
	}
	while ( (L[belong[l]]<l) && (l<=R[belong[l]])) { res+=(a[l]<v), ++l; }
	while ( (L[belong[r]]<=r) && (r<R[belong[r]])) { res+=(a[r]<v), --r; }
	for (int i = belong[l]; i <= belong[r]; ++i) {
		res += upper_bound(b+L[i],b+R[i]+1,v)-(b+L[i]);
	}
	return res;
}

inline void update(int x, int bid)
{
	while ( (L[belong[bid]]<bid) && (b[bid-1]>x) ) {
		swap(b[bid-1], b[bid]);
		swap(num_to_bid[b[bid-1]], num_to_bid[b[bid]]);
		--bid;
	}
	while ( (bid<R[belong[bid]]) && (x>b[bid+1]) ) {
		swap(b[bid], b[bid+1]);
		swap(num_to_bid[b[bid]], num_to_bid[b[bid+1]]);
		++bid;
	}
}

inline void modify(int n_1, int n_2)
{
	// 保证 n_1 在 n_2 左侧
	int l=num_to_aid[n_1], r=num_to_aid[n_2];
	if (l>r) { swap(l,r), swap(n_1,n_2); }
	
	// 更新答案
	ans += (
		2*query(l+1,r-1,n_2)-2*query(l+1,r-1,n_1)
		+ (n_1<n_2? 1: -1)
	);
	
	// 交换
	swap(a[num_to_aid[n_1]], a[num_to_aid[n_2]]);
	swap(num_to_aid[n_1], num_to_aid[n_2]);
	
	if (belong[num_to_bid[n_1]] != belong[num_to_bid[n_2]]) {
		swap(b[num_to_bid[n_1]], b[num_to_bid[n_2]]);
		swap(num_to_bid[n_1], num_to_bid[n_2]);
		update(n_1, num_to_bid[n_1]);
		update(n_2, num_to_bid[n_2]);
	}
}

int main()
{
	// cin.tie(nullptr) -> sync_with_stdio(false);

	// I.N.
	n=read(), q=read();
	
	// 初始化
	init();
	
	// O.P.
	while (q--) {
		int n_1, n_2;
		n_1=read(), n_2=read();
		if (n_1 == n_2) {
			printf("%lld\n", ans); continue;
		}
		modify(n_1, n_2);
		printf("%lld\n", ans);
	}
	
	// E.D.
	return 0;
}

总结

分块的思路：

• 针对题目中要求的操作，找到一种节约时间的整块维护方式；
• 计算复杂度，推导 \(sz\) 的取值；
• 对单点和整块分开处理。

和线段树一样，分块的特点，是易于处理区间可加性问题，但在很多时候，在有限时空限制内无法通过区间相加直接维护出想要的量，此时可以转换思路，间接维护。比如区间众数问题（P4168 [Violet] 蒲公英）就需要换一种储存方式，储存数字出现的下标，而不用桶直接做哈希。比如动态第 \(k\) 大问题（P2617 Dynamic Rankings），可以使用二分答案。

除此之外，分块可以在分完的块内进行排序操作，以维护有序性，便于调用（如 Acwing252 磁力块）。

• TODO：CF1830E
• TODO：IOI2011 Dancing Elephants