堆

本文针对 CSP-S2/NOIP 复习，重点在在哪用、怎么写，底层原理和实现不是重点。

---

堆的概念、应用情景、stl 实现

【堆的概念】

堆是一种可以在 \(O(\log n)\) 的时间内维护一个最值的数据结构，维护最大值的称为大根堆，维护最小值的称为小根堆。

【堆的应用情景】

堆的应用只有一个，就是求最值，但求什么最值、求出最值后怎么用，需要根据题目具体分析。

• 使用对顶堆可以维护第 \(k\%\) 位数（具体见例题 P7072）
• 反悔贪心一般需要维护所做的最劣决策，一般也会用到若干个堆（见反悔贪心）

现在比赛可以用 stl 了，所以就不复习怎么手写堆了，用 priority_queue 就行了。

【存已有的数据类型】

priority_queue <int, vector<int>, greater<int> > q;

• 先声明 priority_queue
• 参数要么只写一个数据类型（像 int、long long ……），要么就三件套，数据类型、vector、比较方式
  • 比较方式有两种，greater<数据类型> 和 less<数据类型>，分别表示当数字大/小时下沉，也就对应了小根堆和大根堆。
  • 需要特别注意：greater 是小根堆！greater 是小根堆！大于表示大数字下沉而小数字在堆顶！
  • 如果只写数据类型而不声明比较方式，默认为大根堆

【存 struct】

• 存 struct 需要重载运算符。
  • 重载的一定是小于号，因为 priority_queue 默认大根堆，调用小于号
  • 重载部分，< 对应大根堆，> 对应小根堆。
• 重载完之后只需要写数据类型就够了，不用再声明比较方式了。

struct node {
	// 这里写一些结构体中的变量
	int x;
	// 这里是重载部分
	const bool <(const node& x) const
	{
		return x < b.x;  // 大根堆
		// return x > b.x; 就是小根堆  
	}
};

priority_queue <node> q;

【堆的删除】

在堆中，除了堆顶之外，具体元素的位置是不清楚的，遍历删除耗时太久，可以用懒删除。（具体见例题 P2061）

例题

题目	备注
P7072 [CSP-J2020] 直播获奖	对顶堆，k%位数
P2061 [USACO07OPEN] City Horizon S	扫描线，堆的懒删除
iai433 分数排序	普通的堆，但比较难想
P2048 [NOI2010] 超级钢琴	前缀和+RMQ+堆，非常难想

P7072 [CSP-J2020] 直播获奖

\(k\%\) 位数问题，是堆的一个经典应用。

解法是对顶堆：开一个大根堆 q 和一个小根堆 p，大根堆存小数字，小根堆存大数字，并且保证总数为奇数时，小根堆的大小恰好为 \(p\times w\%\)。

每当考虑一个新的数字 \(a\) 时，做两步：

• 因为大根堆要存小数字，所以先拿 \(a\) 和 q.top() 进行比较，来决定加入哪个堆中。
• 再调整小根堆的大小，小根堆多就把多出来的数字丢到大根堆，少就从大根堆里弹出堆顶补充。

题目中所求的答案即为小根堆堆顶。

比如对于这组数据：5, 6, 1, 2, 7, 4, 1、\(w=50\)。
假设我们已经知道了前五个数的 \(50\%\) 位数是 5。
则现在大根堆中的数据：2, 1，小根堆中的数据为 5, 6, 7。

处理接下来一个数字 4，在这里，因为 4 比大根堆堆顶 2 大，所以加入小根堆。
现在小根堆中有 4 个数字：4, 5, 6, 7，而 \(p\times w\%=3\)，所以把小根堆堆顶 4 弹出，放到大根堆。
现在大根堆中的数据：4, 2, 1，小根堆中的数据为 5, 6, 7，输出答案 5。

再处理接下来一个数字 1，比大根堆堆顶 4 小，所以加入大根堆
现在大根堆中的数据：4, 2, 1, 1，小根堆中的数据为 5, 6, 7，\(p\times w\%=4\)。
调整大小，把大根堆堆顶 4 弹出放入小根堆。
现在大根堆中的数据：2, 1, 1，小根堆中的数据为 4, 5, 6, 7，输出答案 4。

实现方面，只需要用两个 priority_queue 即可。

AC 代码提交记录

#include <bits/stdc++.h>

using namespace std;

int n, w;
priority_queue <int> q;
priority_queue <int, vector<int>, greater<int>> p;

int main()
{
	cin >> n >> w;
	for (int i = 1; i <= n; ++i) {
		int x, k=max(1, i*w/100);
		cin >> x;
		if (q.empty() || x > q.top()) {
			p.push(x);
		} else {
			q.push(x);
		}
		while (!p.empty() && p.size() > k) { q.push(p.top()); p.pop(); }
		while (!p.empty() && p.size() < k) { p.push(q.top()); q.pop(); }
		cout << p.top() << " ";
	}
	return 0;
}

P2061 [USACO07OPEN] City Horizon S

矩形面积并，一眼【扫描线】。

从左往右，在有建筑开始或结束的地方，放一条假想的、垂直于地平线的【扫描线】，对合并完之后的那个奇形怪状的图形做切割。

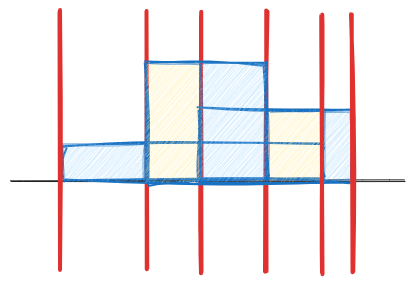
这样一来，每次切割出来的部分是一个矩形。面积可以拿相邻两条扫描线的距离差 \(\Delta x\)，乘上这段里面的高度最大值 \(h_{max}\)。答案是这 \(2n\) 条扫描线切割出来的面积之和，即 \(S=\sum(\Delta x\times h_{max})\)。

因为扫描线是人为定下来的，\(\Delta x\) 很好求，难点在于如何维护 \(h_{max}\)。二维平面上的扫描线需要用到线段树，但在这里，因为题干中有地平线的存在，只需要拿一个堆即可。

假设我们已经维护出了前 \(i\) 条扫描线 \(bd_i\)，对于第 \(i+1\) 条扫描线 \(bd_{i+1}\)：

• 两条扫描线之间的距离差为 \(\Delta x=bd_{i+1}.x-bd_i.x\)，从堆中取出 \(h_{max}\)，将 \(\Delta x\times h_{max}\) 计入答案。
• 如果这条扫描线标记了某一幢建筑的【起点】，那么将这幢建筑的高度加入堆中。
• 如果这条扫描线标记了某一幢建筑的【终点】，那么执行删除操作。

接下来介绍堆的删除操作：【懒删除】。

因为在堆中，我们只能很快知道堆顶的元素，对于具体元素的位置需要遍历整个堆，时间吃不住。

但是，我们可以发现，如果被删去的元素不在堆顶，那么将不会从堆中取出被删去的元素，进而也就不会对答案产生影响。

所以我们可以用 flag 数组，或者 cnt 数组，或者再开一个堆，记下所有要删除的元素。
每次从堆中取出元素时，检查它是否被删除，然后才真正执行删除操作。

当然，在这题中，可以比较当前扫描线的位置，和取出的高度所代表的这幢楼的终点的位置，也可以判断取出的 \(h_{max}\) 是否合法。

AC 代码提交记录

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int MAXN=4e4+5;
int n;
ll ans;

struct node {
	ll x, h;
	bool st;
} bd[MAXN<<1];

priority_queue <ll> q, del_q;

int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		long long a, b, h; cin >> a >> b >> h;
		bd[2*i-1] = { a, h, 1 };
		bd[2*i]   = { b, h, 0 };
	}
	sort(bd+1, bd+2*n+1, [](node a, node b){return a.x<b.x;});
	for (int i = 1; i <= 2*n; ++i) {
		while ( (!q.empty()) && (!del_q.empty()) && (q.top() == del_q.top())) { q.pop(); del_q.pop(); }
		if (!q.empty()) { ans += q.top() * (bd[i].x-bd[i-1].x); }
		if (bd[i].st) { q.push(bd[i].h); }
		else            { del_q.push(bd[i].h); }
	}
	cout << ans << endl;
}

iai433 分数排序

\(\displaystyle\frac ab\) 是最简真分数，等价于 \(a,b\) 互质，等价于 \(\gcd(a,b)=1\)。

把所有分数都罗列出来，复杂度是平方级别的，显然吃不住，只能拿 60 分，所以只能从小到大一个一个看。

• 如果分母相同，分子越小，分数越小。
• 如果分子相同，分母越大，分数越小。
• 如果分子分母都不相同，就没办法快速比较了。

所以这里可以用堆维护最小的分数，相同分母的分数，只要选最小的那个加入堆即可。

初始时，堆中有 \(n-1\) 个元素，分别为 \(\displaystyle\frac12, \frac13, \cdots, \frac1n\)。每次取出最小的那一个 \(\displaystyle\frac ab\)，然后考虑下一个以 \(b\) 为分母的分数 \(\displaystyle\frac{a+1}{b}\)，如果是最简真分数就入堆，不合法就再枚举下一个。

AC代码提交记录

#include <bits/stdc++.h>

using namespace std;

const int MAXK=2e5+5;
int n, k, cnt;

struct node {
	int a, b;
	double a_b;
	bool operator <(const node &x) const
	{
		return a_b > x.a_b;
	}
} num;

priority_queue <node> q;

int main()
{
	cin >> n >> k;
	for (int i = 2; i <= n; ++i) { q.push({1, i, double(1)/i}); }
	node c;
	for (int i = 1; i <= k; ++i) {
		c=q.top(); q.pop();
		int a = c.a + 1;
		while ( (a < c.b) && (__gcd(a,c.b)!=1) ) { ++a; }
		q.push( {a, c.b, double(a)/c.b} );
	}
	cout << c.a << "/" << c.b << endl; return 0;
}

P2048 [NOI2010] 超级钢琴

要求长度在 \([L,R]\) 的前 \(k\) 个最大连续子段和（超级和弦）之和，总的数量是 \(O(n^2)\)，如果暴力枚举，可以使用前缀和优化，再用堆维护现在前 \(k\) 大超级和弦中的最小值，打擂台，时间复杂度 \(O(n^2log k)\)。

想要优化，就必然不能把 \(O(n^2)\) 种情况全部枚举一遍。可以类比 [[iai433]] 的做法，对于一类超级和弦，只将最大的那一个加入堆中，每当从堆中取出一个超级和弦时，再将次大的超级和弦加入。

具体而言，假设我此时考虑的超级和弦起点为 \(st\)，终点 \(ed\) 的取值范围为 \([st+L-1, st+R-1]\)。不妨设该区间为 \([l,r]\)，于是我们可以用一个三元组 \((st,l,r)\) 描述以 \(st\) 为起点，终点 \(ed\) 范围在 \([l,r]\) 的超级和弦。

这样一来，设前缀和数组为 \(s[i]\)，这段超级和弦的美妙度可以用前缀和描述为 \(s[ed]-s[st-1]\)，由于左端点固定，当 \(s[ed]\) 取到最大值（设该位置为 \(t\)）时，这段超级和弦的美妙度也取到了最大值，即 \(s[t]-s[st-1]\)。而这个求 \(t\) 和 \(s[t]\) 的步骤，可以使用 ST 表在 \(O(1)\) 的时间内完成。

接下来，对于这一类超级和弦 \((st,l,r)\)，要取它们中的次大值。

可想而知的是，区间 \([l,r]\) 内的最大值 \(s[t]\) 已经被取掉，次大值只能在区间 \([l,t)\cup(t,r]\) 中。于是此时，我们可以将 \((st,l,t-1)\) 和 \((st,t+1,r)\) 加入堆中，进而将【求次大值】转化为与【求最大值】同构的子问题（注意特判 \(l>t-1\) 和 \(t+1>r\) 的情况）。

由题意得，我们需要从堆中恰好取出 \(k\) 段超级和弦，而每次取出后，至多只会往堆中加入 \(2\) 段新的超级和弦，于是堆的大小规模为 \(O(2k)=O(k)\)。不会爆空间。

整体的流程如下：

1. 对于输入的美妙度 \(a[i]\)，求其前缀和 \(s[i]\)，时间复杂度 \(O(n)\)；
2. 对前缀和数组 \(s[i]\) 建立 ST 表，预处理时间复杂度 \((n\log n)\)；
3. 将所有超级和弦按照起点分类，以三元组 \((st,l,r)\) 的形式加入堆中，时间复杂度 \(O(n \log n)\)；
4. 从堆中取出美妙度最大的超级和弦，将美妙度 \(s[t]\) 累加计入答案，将次小值可能在的两个区间以三元组 \((st,l,t-1)\) 和 \((st,t+1,r)\) 的形式加入堆中，重复，直到累计取出 \(k\) 段超级和弦为止，时间复杂度 \(O(k\log k)\)；
5. 输出答案。总时间复杂度 \(O(n\log n+k\log k)\)

AC 代码提交记录

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int MAXN=5e5+5, MAXI=20;
int n, k, L, R, p[MAXN][MAXI+5];
ll a[MAXN], s[MAXN][MAXI+5], ans;

pair<ll,int> query(int l, int r)
{
	int i = log2(r-l+1);
	ll  lv=s[l][i], rv=s[r-(1<<i)+1][i];
	int lp=p[l][i], rp=p[r-(1<<i)+1][i];
	if (lv < rv) { return make_pair(rv,rp); }
	else         { return make_pair(lv,lp); }
}

struct node {
	int st, l, r, p;
	ll x;
	bool operator < (const node &c) const {
		return x < c.x;
	}
};

node new_node(int st, int l, int r)
{
	int pos; ll val;
	tie(val,pos) = query(l,r);
	return (node){ st, l, r, pos, val-s[st-1][0] };
}

priority_queue <node> q;

int main()
{
	cin >> n >> k >> L >> R;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		s[i][0] = s[i-1][0] + a[i];
		p[i][0] = i;
	}

	// 建立 st 表
	for (int i = 1; i <= MAXI; ++i) {
		for (int j = 1; j+(1<<(i-1)) <= n; ++j) {
			ll  lv=s[j][i-1], rv=s[j+(1<<(i-1))][i-1];
			int lp=p[j][i-1], rp=p[j+(1<<(i-1))][i-1];
			if (lv < rv) { s[j][i]=rv; p[j][i]=rp; }
			else         { s[j][i]=lv; p[j][i]=lp; }
		}
	}

	// 建堆
	for (int i=1, l=i+L-1, r=i+R-1; l <= n; ++i, ++l, ++r) {
		r = min(n, r);
		q.push( new_node(i,l,r) );
	}

	// 选取前 k 个
	for (int i = 1; i <= k; ++i) {
		node c = q.top(); q.pop();
		ans += c.x;
		if (c.l <= c.p-1) { q.push( new_node(c.st, c.l, c.p-1) ); }
		if (c.p+1 <= c.r) { q.push( new_node(c.st, c.p+1, c.r) ); }
	}

	// E.D.
	cout << ans << endl;
	return 0;
}