斜率优化

前置知识

分组 dp

很多情况下，斜率优化会出现在分组 dp 的题里面。
不限制组数，“1D/1D”：\(\displaystyle f(i)=\min_{1\leq j < i}\{ f(j)+val(j+1,i)\}\)。
有限制组数，“2D/1D”：\(\displaystyle f(i,k)=\min_{1\leq j < i} \{ f(j,k-1)+val(j+1,i) \}\)。

斜率优化的原理

针对 \(\displaystyle f(i)=\min_{0\leq j < i}\{ -K_iX_j+Y_j \}\) 进行优化。
注意：\(K_i\) 只跟 \(i\) 有关而不跟 \(j\) 有关，\(X_j\) 同理，常数部分归到哪里都是可以的。

上述方程如果【朴素】实现，时间复杂度是 \(O(n^2)\)，因为首先需要一层循环枚举 \(i\)，然后需要再枚举 \(j\) 找到最小值。
既然是进行【优化】，那么必然需要【略去】一些部分不加以计算，从而达到降低复杂度的效果。

数形结合

我们可以将上述式子中的 \((X_j,Y_j)\) 抽象为平面上的一些点。

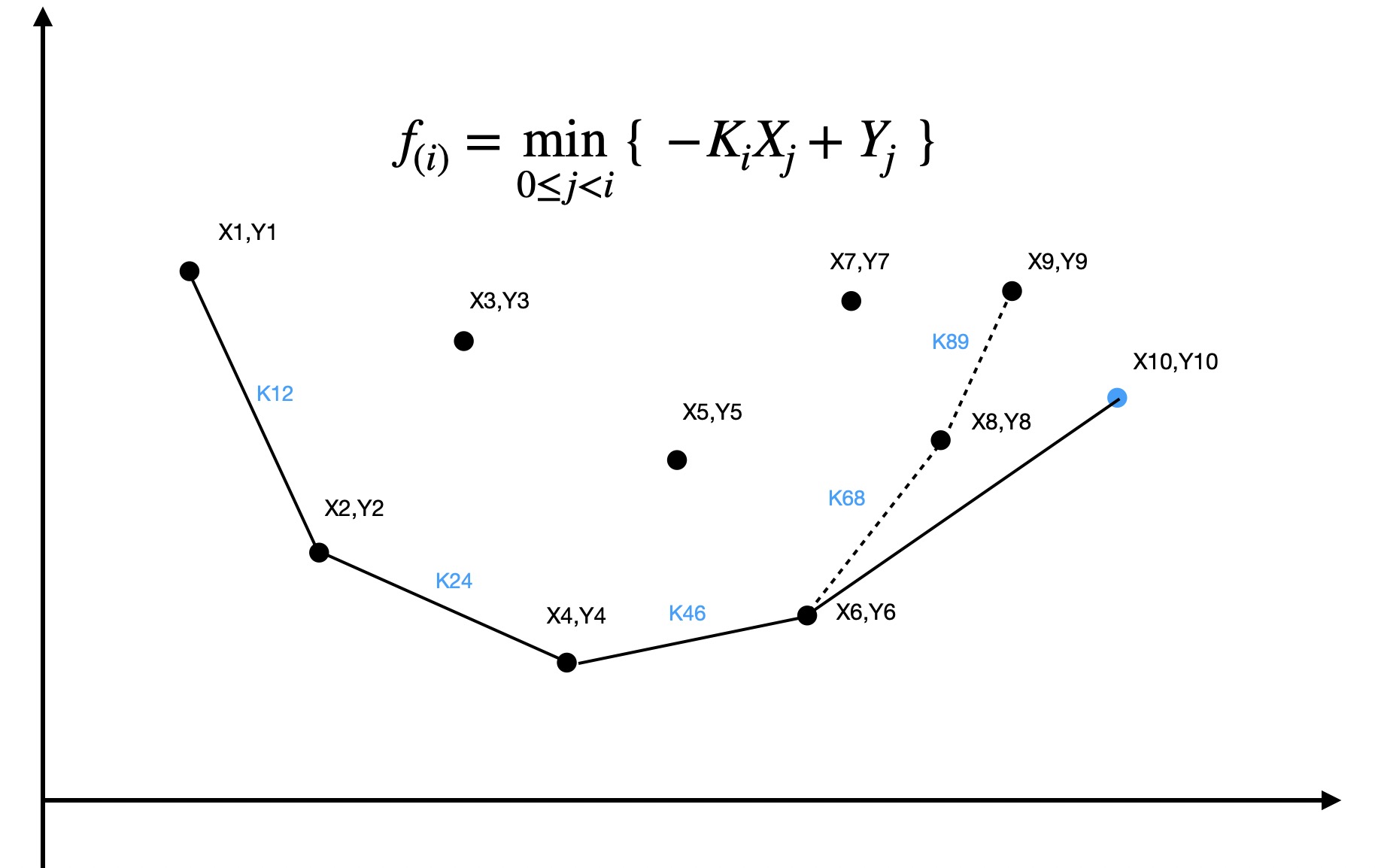
（图是老师上课的课件）
在这张图上，\(-K_iX_j+Y_j\) 对应的几何意义为：一条【斜率】为 \(K_i\) 且经过 \((X_j,Y_j)\) 的直线，在【纵轴上的截距】。
我们考虑，当枚举到 \(i\) 的时候，我们可以确定的是这条直线的斜率 \(K_i\)，并且我们已知前面的所有点 \((X_j,Y_j)\)。
我们可以想象一条直线从纵轴负无穷【逐渐向上】。
不难发现，图中【黑线往上】的点，都是【不必枚举】的，因为在碰到黑线往上的点之前，就已经【先碰到】恰好在黑线上的点了。
于是，只要能够用合理的方法【维护】出这条黑线，并利用其【快速求解】，我们就完成了优化的过程。

凸包的概念

我们可以用更形式化的语言描述图中的黑线。
观察图，我们可以发现，从左到右，黑线的【斜率】是【递增】的。
如果有一系列点，【相邻两点】连线的【斜率】是【递增】或【递减】的，那么我们称其为【凸包】。
（斜率递增时，直线先向下，再逐渐向上，和图中情况一样，称为下凸包，反之则为上凸包）
我们称上文所述的【黑线往上】为【在（下）凸包内部】

如何维护凸包（\(X_j\) 单调递增）

我们考虑 \(X_j\)【单调递增】的情况，我们可以用【单调队列】维护凸包。
我们可以观察图中的虚线部分，当枚举到 \(X_9\) 的时候，虚线部分是【此时】的凸包。
当枚举到 \(X_{10}\) 的时候，8 号点与 9 号点的连线斜率 \(K_{8-9}>K_{9-10}\)，所以此时 9 号点来到了凸包内部。
此时我们就应该从单调队列中【删去】9 号点，并【接着考虑】8 号点是否也应该被删去。
这个过程一直做到 6 号点，4—6—10 是一个合法的凸包。

上述过程可以总结为以下的步骤：

枚举到点 \(i\)，求出此时第 \(i\) 号点的坐标 \((X_i,Y_i)\)
看单调队列队尾的第 \(k\) 号点，是否满足 \(k-1\rightarrow k\rightarrow i\) 符合凸包的性质
- 如果不满足，删除队尾，重复这一步
- 如果满足，则到这一步已经维护出了一个合法的凸包，结束
  可以用如下的代码描述：

int head, tail;

// 这里是为了方便计算，用了宏定义，括号内的内容需要具体填充
#define y(j) ()
#define x(j) ()
#define k(i) ()
#define IC(i,j) (y(j)-k(i)*x(j))
#define slope(i,j) ((long double)(y(i)-y(j))/(x(i)-x(j)))

bool check(int i, int j, int k)
{
    return slope(k,j) <= slope(j,i);
}

for (int i = 1; i <= n; ++i) {
	// 维护凸包
	while ( (head<tail) && (check(q[tail-1], q[tail], i)) ) { --tail; }
	q[++tail] = i;
}

如何求解答案（\(K_i\) 单调递增）

我们不难发现，求解答案的过程，实际上就是找到 \(K_i\) 的大小应该【位于】单调队列的何处。
如果 \(K_{p_1-p_2}\leq K_i\leq K_{p_2-p_3}\)，那么 \(p_2\) 就是此时的决策点。

（图片来自 OI-wiki）
在 \(K_i\) 单调递增的情况下，我们可以不断【从队首删去元素】，这样就可以快速地找到决策点进行转移。
具体过程可以用如下代码实现

for (int i = 1; i <= n; ++i) {
	// 维护决策点
	while ( (head<tail) && (IC(i,q[head])>=IC(i,q[head+1])) ) { ++head; }
	f[i] = ...;  // 此处进行转移
}

完整板子（\(X_j\) 和 \(K_i\) 都单调递增）

int head, tail;

// 这里是为了方便计算，用了宏定义，括号内的内容需要具体填充
#define y(j) ()
#define x(j) ()
#define k(i) ()
#define IC(i,j) (y(j)-k(i)*x(j))
#define slope(i,j) ((long double)(y(i)-y(j))/(x(i)-x(j)))

bool check(int i, int j, int k)
{
    return slope(k,j) <= slope(j,i);
}

for (int i = 1; i <= n; ++i) {
	// 维护决策点
	while ( (head<tail) && (IC(i,q[head])>=IC(i,q[head+1])) ) { ++head; }
	f[i] = ...;  // 此处进行转移
	// 维护凸包
	while ( (head<tail) && (check(q[tail-1], q[tail], i)) ) { --tail; }
	q[++tail] = i;
}

TODO：此处仅讨论的 \(X_j\) 和 \(K_i\) 都单调的情况，如果不单调情况会复杂很多，俺也不会……

例题

iai480 排版问题

朴素 dp

写 dp 方程的这一步，就是直接套分组 dp 的板子。
设 \(f[i]\) 表示截至第 \(i\) 个单词的最小偏离度。
设 \(s[i]\) 是字符长度 \(w[i]\) 的前缀和数组。
把第 \(j+1\) 到第 \(i\) 个物品分在一起，套用题干中的 \((x-a)^2\) 计算其对答案的贡献，应该是 \((s[i]-s[j]-a)^2\)。
于是有：\(f[i] = min\{ f[j]+(s[i]-s[j]-a)^2 \}\)。

优化过程

设 \(k[i]=2(s[i]-a)\)，将上述状态转移方程展开，有如下结果：

\[f[j] + \frac{k[i]^2}{4} - k[i]\times s[j] + s[j]^2 \]

于是套用斜率优化的板子，可以设：

\[\begin{cases} y[j] = f[j]+s[j]\times s[j] \\ x[j] = s[j] \\ IC(i,j) = y[j]-k[i]\times x[j] \\ \end{cases} \]

完整代码

#include <bits/stdc++.h>

using namespace std;

const int MAXN=2e5+5;
int n, a;
long long s[MAXN], f[MAXN];
deque <int> q;

/*
最小化sum{ (x-a)^2 }

分组dp，设f[i]表示截至第i个单词，最小偏离度
f[i] = min{ f[j]+(s[i]-s[j]-a)^2 }

设k[i]=2*(s[i]-a)，将上述状态转移方程展开
f[j] + (1/4)*k[i]^2 - k[i]*s[j] + s[j]^2

y[j]    = f[j]+s[j]*s[j]
x[j]    = s[j]
IC(i,j) = y[j]-k[i]*x[j]
*/

#define k(i) (2*(s[i]-a))
#define y(j) (f[j]+s[j]*s[j])
#define x(j) (s[j])
#define IC(i,j) (y(j)-k(i)*x(j))

bool check(int i, int j, int k)
{
    return (
        (y(j)-y(i))*(x(k)-x(j)) >= (y(k)-y(j))*(x(j)-x(i))
    );
}

int main()
{
//    freopen("iai480_1.in", "r", stdin);
    cin.tie(nullptr) -> sync_with_stdio(false);

    // I.N.
    cin >> n >> a;
    for (int i = 1; i <= n; ++i) {
        int w; cin>>w;
        s[i] = s[i-1] + w;
    }

    // D.P.
    q.push_back(0);
    for (int i = 1; i <= n; ++i) {
        while ( (q.size()>1) && (IC(i,q[0])>=IC(i,q[1])) ) { q.pop_front(); }  // 从左侧开始，看从哪个转移
        f[i] = f[q[0]] + (s[i]-s[q[0]]-a)*(s[i]-s[q[0]]-a);
        while ( (q.size()>1) && (check( q[q.size()-2], q.back(), i )) ) { q.pop_back(); }  // 从右侧开始，维护凸包
        q.push_back(i);
    }

    // E.D.
    cout << f[n] << endl;
    return 0;
}

备注及实现细节

关于斜率计算

注意板子中的 check()，有两种写法，一种是开 long double 用除法，另一种是交叉相乘。
- 后者不用考虑精度丢失的问题，但毒瘤题目可能会爆 long long。
- 有的题目可能会出现两个 \(X\) 相同的情况，此时需要特判为 +inf
斜率可正可负，不能开 unsigned long long，所以斜率优化的题范围不可能太极限。

关于题目套路

斜率优化的题都比较偏板子，如果真有难点，也是怎么写朴素 dp。
理解斜率优化的原理、板子打熟，斜优部分就是顺手一加。
斜率优化还可能和别的优化套在一起（尤其是 wqs 二分）

题单

题目	AC 代码提交记录	备注
iai480 排版问题	https://iai.sh.cn/submission/592286	例题
P3195 [HNOI2008] 玩具装箱	https://www.luogu.com.cn/record/105652174	和例题非常像
P3628 [APIO2010] 特别行动队	https://www.luogu.com.cn/record/108080155	偏板子
P2120 [ZJOI2007] 仓库建设	https://www.luogu.com.cn/record/108069165	出现了斜率为 `inf` 的情况（hack）
P2900 [USACO08MAR] Land Acquisition G	https://www.luogu.com.cn/record/107436024	写朴素 dp 的过程有一点思维难度
P5785 [SDOI2012] 任务安排	https://www.luogu.com.cn/record/108055923	从 \(O(n^3)\) 写到 \(O(n^2)\) 的朴素 dp 很有难度

posted @ 2023-08-11 21:06 LittleDrinks 阅读(35) 评论(0) 收藏举报

刷新页面返回顶部

LittleDrinks