最短路问题
最短路问题(sp),即在图上求出两点之间总权值之和最小的路径。
最短路问题分为单源最短路(sssp)和多源最短路(mssp),前者只需要求出一个点到其余所有的最短路径权值和,而后者要求出图上任意两点的最短路径权值和。
最短路问题有以下集中常见算法:(设所给有向图中有 \(n\) 个点,\(m\) 条边)
| 算法 | 应用 | 时间复杂度 | 备注 |
|---|---|---|---|
| Floyd | mssp / sssp | \(O(n^3)\) | |
| heap-Dijkstra | sssp | 二叉堆优化后 \(O((n+m)\log n)\) | 不能处理负环 |
| Bellmen-Ford / spfa | sssp | \(O(nm)\) | 能处理负环 会被卡掉 “关于 spfa,它已经死了”,详见这篇 |
本文中,所有“松弛”操作的定义为:如果 \(u\rightarrow k\rightarrow v\) 的路径比 \(u\rightarrow v\) 的路径短,那么将这两点间的距离更新为前者。
if (dis[u][v] > dis[u][k] + dis[k][v]) {
dis[u][v] = dis[u][k] + dis[k][v];
}
任意两点最短路——Floyd
Floyd 算法的本质是 dp。
设 \(f[k][u][v]\) 表示经过点 \(k\) 松弛后 \(u\rightarrow v\) 的最短路径权值和。
刚开始:
求最短路的过程就是不断松弛的过程,其状态转移方程为:
Floyd 需要三层循环,分别枚举中转点、起点、终点,这三层循环的顺序是 Floyd 算法唯一需要注意的地方。
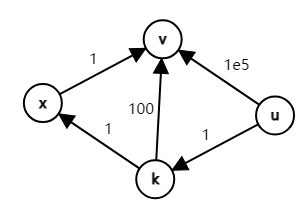
如图所示,我们考虑把枚举起点放在最外层循环,第一个枚举到的是 \(u\),此时最优选择是通过 \(k\) 中转,最短路为 \(u\rightarrow k\rightarrow v\),由于 \(k\) 点出发的最短路尚未更新,此时 \(u\rightarrow v\) 的最短路权值为 \(101\)。而之后从 \(u\) 出发的最短路将不再有机会更新,所以权值为 \(3\) 的最短路 \(u\rightarrow k\rightarrow x\rightarrow v\) 并没有被找到。
枚举终点同理会有问题,因此,枚举中转点 \(k\) 应该放在最外层循环。
最后,可以使用滚动数组优化空间。时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\)。
for (int k = 1; k <= n; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++i) {
f[i][j] = min( f[i][j], f[i][k]+f[k][j] );
}
}
}
B3611 【模板】传递闭包
无向图上任意两点可达性可以通过并查集维护。
有向图上任意两点可达性可以通过 Floyd 求出。
邻接矩阵存图,使用 std::bitset 可以将时间复杂度优化到 \(O(\dfrac{n^3}{w})\),可以处理 \(2000\) 左右的数据。
#include <bits/stdc++.h>
using namespace std;
const int N=105;
int main()
{
int n; cin >> n;
bitset <N> b[N];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
int x; cin >> x;
b[i][j] = x;
}
}
for (int j = 1; j <= n; ++j) {
for (int i = 1; i <= n; ++i) {
if (b[i][j]) { b[i] |= b[j]; }
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
cout << char(b[i][j]+'0') << " ";
}
cout << "\n";
}
}
单源最短路——从bfs讲起
从某个点出发,尝试更新周围点的最短路,如果成功了就将其加入队列留待继续更新,这是非常朴素的 bfs 算法。
bfs 算法在最短路问题上有非常多应用。比如通过建立超级源点,bfs 算法可以处理多个起点的最短路问题。比如在走迷宫等可以转化为单位边权图的问题上,bfs 可以在 \(O(n)\) 的时间内求出所有点的最短路。
只有从最短路已经确定的点出发,才可能求出最短路。单位边权图上最短路一定是按照 bfs 遍历的顺序求出,因此 bfs 算法在其上的复杂度非常优秀。但拓展到任意边权的图上就没有“顺序求得最短路”这一性质了。从最短路尚未求出的点 \(u\) 出发向外松弛是无用的,因为一旦 \(u\) 被松弛,之前的操作就需要一摸一样地再进行一遍。
也就是说,我们需要仔细考虑任意边权图上 bfs 复杂度的退化情况,或是按照某些性质选定队列内点遍历的顺序,才能在一个可以接受的复杂度内套用 bfs 算法。
spfa(Bellman-Ford)
Bellman-Ford 算法指出,在一张无负环的任意边权图上,每花费 \(O(m)\) 的时间对所有边进行一次松弛,可以使最短路的长度加一。因此最多 \(O(nm)\) 次松弛操作就可以求出所有点的最短路。
spfa 是 Bellman-Ford 算法的队列实现。很多时候我们并不需要那么多无用的松弛操作。很显然,只有上一次被松弛的结点所连接的边,才有可能引起下一次的松弛操作。那么我们用队列来维护【哪些结点可能会引起松弛操作】,就能只访问必要的边了。[1]
不难发现,其实 spfa 就是 bfs,它和 Bellman-Ford 算法等价,而 Bellman-Ford 证明了其算法的复杂度最劣为 \(O(nm)\),所以我们就可以继续愉快地 bfs 了。
稀疏图上 spfa 效率较高,但可以被随意构造的菊花图卡成 \(O(nm)\)。
void spfa()
{
queue<int> q;
for (int i = 1; i <= n; ++i) {
dis[i] = inf;
vis[i] = 0;
}
q.push(s); dis[s]=0; vis[s]=true;
while (!q.empty()) {
int u=q.front(); q.pop(); vis[u]=0;
for (int i = head[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (dis[v] > dis[u]+e[i].val) {
dis[v] = dis[u]+e[i].val;
if (!vis[v]) {
vis[v] = true;
q.push(v);
}
}
}
}
for (int i = 1; i <= n; ++i) {
cout << dis[i] << " ";
}
}
P3385 【模板】负环
由于负环的存在,边权会越绕越小,因此图中不存在最短路,Dijkstra 会在这里被卡成 TLE。
显然在实际应用中我们无法使用 TLE 判负环法。
使用 spfa,在求最短路的过程中记录一下最短路经过的点的数量 \(viscnt\),如果 \(viscnt\) 大于 \(n-1\) 说明在负环上绕圈了。
#include <bits/stdc++.h>
using namespace std;
const int N=2e3+5;
const int inf = INT_MAX;
int n, m;
vector <pair<int,int>> G[N];
bool spfa(int s=1)
{
queue <int> q;
vector <int> dis(n+1, inf), cnt(n+1, 0);
vector <bool> inq(n+1, false);
dis[s] = 0;
inq[s] = true;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = false;
for (auto& [v, w]: G[u]) {
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
cnt[v] = cnt[u] + 1; // 最短路径上的节点数量,无负环则至多为 n-1
if (cnt[v] >= n) { return true; }
if (!inq[v]) { q.push(v); inq[v] = true; }
}
}
}
return false;
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) { G[i].clear(); }
for (int i = 1; i <= m; ++i) {
int u, v, w;
cin >> u >> v >> w;
if (w >= 0) {
G[u].push_back( {v, w} );
G[v].push_back( {u, w} );
} else {
G[u].push_back( {v, w} );
}
}
if (spfa()) { cout << "YES\n"; }
else { cout << "NO\n"; }
}
int main()
{
int t; cin >> t;
while (t--) { solve(); }
}
Dijkstra
Dijkstra 算法指出,在边权非负的图上,尚未访问到的点中,距离最小的那一个最短路一定已经求出。
只需要把 bfs 的队列换成优先队列即可。
可以使用 Dijkstra 寻找有向图上的最小环。枚举图上的一个点 \(u\) 作为环的起点,跑一遍 Dijkstra 求出点 \(u\) 到剩下所有点 \(v\) 的最短距离。如果有一条 \(v\to u\) 的边,那么就找到了一个环,环的权值为 \(dis[v]+w(v,u)\)。最终时间复杂度 \(O(NM\log N)\)。
以下给出 Dijkstra 找最小环的示例代码。
void Dijkstra(int s)
{
priority_queue <pii, vector<pii>, greater<pii>> q;
for (int i = 1; i <= n; ++i) { vis[i]=0; dis[i]=inf; }
dis[s] = 0;
q.push( {0, s} );
while (!q.empty()) {
int u = q.top().second; q.pop();
if (vis[u]) { continue; }
vis[u] = 1;
for (auto [v,p]: G[u]) {
if (dis[v] > dis[u] + p) {
dis[v] = dis[u] + p;
if (!vis[v]) { q.push( {dis[v], v}); }
}
// 与 Dijkstra 唯一的区别
if (v == s) { mnc = min(mnc, dis[u]+p); }
}
}
}
如果你觉得已经学会了单源最短路的话,尝试写一写 P4779 【模板】单源最短路径(标准版)吧
题单
| 题号 | 备注 |
|---|---|
| B3611 | 传递闭包 |
| P3385 | 负环模板题 |
| P4779 | 单源最短路模板 |
| CF2041D | bfs |
| gym103409E | 有向图上找最小环 |
| gym103409K | 最短路分层 |
| gym105386J | ST 表维护二元距离 |
CF2041D. Drunken Maze
用 \((x,y,d,cnt)\) 表示到达某个节点时的坐标、方向、步数,然后大力 bfs 即可。
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
const int dx[]={1,0,-1,0}, dy[]={0,1,0,-1};
int main()
{
int n, m;
cin >> n >> m;
vector <string> mp(n);
map <array<int,4>, int> dis;
int stx, sty, edx, edy;
for (int i = 0; i < n; ++i) { cin >> mp[i]; }
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (mp[i][j] == 'S') { stx=i; sty=j; }
if (mp[i][j] == 'T') { edx=i; edy=j; }
}
}
queue <array<int,4>> q;
q.push({stx, sty, 0, 0});
while (!q.empty()) {
auto [nowx, nowy, d, cnt] = q.front(); q.pop();
if (nowx==edx && nowy==edy) {
cout << dis[{nowx,nowy,d,cnt}] << "\n"; return 0;
}
for (int i = 0; i < 4; ++i) {
int tx = nowx + dx[i];
int ty = nowy + dy[i];
if (0<=tx && tx<=n-1 && 0<=ty && ty<=m-1 && mp[tx][ty]!='#') {
if (i != d) {
if (!dis.count({tx,ty,i,1})) {
dis[{tx,ty,i,1}] = dis[{nowx,nowy,d,cnt}] + 1;
q.push({tx,ty,i,1});
}
} else {
if (cnt < 3 && !dis.count({tx,ty,i,cnt+1})) {
dis[{tx,ty,i,cnt+1}] = dis[{nowx,nowy,d,cnt}] + 1;
q.push({tx,ty,i,cnt+1});
}
}
}
}
}
cout << -1 << "\n";
}
gym103409E. Buy and Delete
一共只有三种情况。
- 如果爱丽丝能够在图上构造出若干个环,那么鲍勃至少需要先用一步把所有环破坏掉,再用一步把剩下的边全部删掉。显然,一种可行的策略是,鲍勃可以选择先删除所有 \(u<v\) 的边 \(u\to v\),再删除 \(u>v\) 的边 \(u\to v\)。因此如果图上有环,那么鲍勃只需要两步就能结束游戏。
- 如果爱丽丝无法构造出一个环,但有钱买得起若干条边,那么鲍勃只需要一步就可以把边全部删光。
- 如果爱丽丝一条边都买不起,那么鲍勃一步都不需要,游戏就结束了。
于是这道题转化为:求有向图上的最小环。枚举图上的一个点 \(u\) 作为环的起点,跑一遍 Dijkstra 求出点 \(u\) 到剩下所有点 \(v\) 的最短距离。如果有一条 \(v\to u\) 的边,那么就找到了一个环,环的权值为 \(dis[v]+val(v,u)\)。最终时间复杂度 \(O(N(N+M)\log N)\)。
#include <bits/stdc++.h>
#define inf 1e18
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const int N=2005;
int n, m, c, vis[N];
ll dis[N], mnc=inf, mne=inf;
vector <pii> G[N];
void Dijkstra(int s)
{
priority_queue <pii, vector<pii>, greater<pii>> q;
for (int i = 1; i <= n; ++i) { vis[i]=0; dis[i]=inf; }
dis[s] = 0;
q.push( {0, s} );
while (!q.empty()) {
int u = q.top().second; q.pop();
if (vis[u]) { continue; }
vis[u] = 1;
for (auto [v,p]: G[u]) {
if (dis[v] > dis[u] + p) {
dis[v] = dis[u] + p;
if (!vis[v]) { q.push( {dis[v], v}); }
}
if (v == s) { mnc = min(mnc, dis[u]+p); }
}
}
}
int main()
{
cin >> n >> m >> c;
for (int i = 1; i <= m; ++i) {
int u, v; ll p;
cin >> u >> v >> p;
G[u].push_back( {v,p} );
mne = min(mne, p);
}
for (int u = 1; u <= n; ++u) { Dijkstra(u); }
if (c >= mnc) { cout << 2 << endl; }
else if (c >= mne) { cout << 1 << endl; }
else { cout << 0 << endl; }
}
gym103409K. Tax
每个点只能由最短路径到达。先跑一边最短路求出距离,按距离将图分层。然后跑一遍 dfs,当且仅当 \(dis[v]=dis[u]+1\) 时通过 \((u,v)\) 继续向下遍历。
考虑如何计算复杂度。
这个问题等价于,将一个正整数 \(n\) 划分为若干正整数 \(a_i\) 的和,求 \(\max\{\prod a_i\}\).
首先可以通过平方差公式证明,\(a\) 中任意两个数字最多相差 \(1\)。然后这个问题变为求 \(f(x)=x^{n/x}\) 的最大值。利用对数求导法求得 \(\displaystyle f'(x)=\frac{n(1-\ln x)}{x^2}\),当 \(x=e\) 时有 \(f(x)_{max}=f(e)=e^{n/e}\)。
因此,当每层都只有三个点时,有复杂度最大值 \(O(3^{\frac{N}{3}})\),可以通过本题。
#include <bits/stdc++.h>
#define inf 1e18
#define mp make_pair
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N=55, M=3005;
int n, m, w[M], t[M];
ll dis[N], vis[N], ans[N];
vector <pii> G[N];
void Dijkstra()
{
priority_queue <pii, vector<pii>, greater<pii>> q;
for (int i = 1; i <= n; ++i) { dis[i] = inf; }
dis[1] = 0;
q.push( {0,1} );
while (!q.empty()) {
int u = q.top().second; q.pop();
if (vis[u]) { continue; }
vis[u] = true;
for (auto [v,c]: G[u]) {
if (dis[v] > dis[u] + 1) {
dis[v] = dis[u] + 1;
if (!vis[v]) { q.push(mp(dis[v], v)); }
}
}
}
#ifndef ONLINE_JUDGE
for (int i = 1; i <= n; ++i) { printf("dis[%d]=%d\n", i, dis[i]); }
#endif
}
void dfs(int u, int fa, ll ww)
{
#ifndef ONLINE_JUDGE
printf("current node %d :: %lld\n", u, fa);
#endif
ans[u] = min(ans[u], ww);
for (auto [v,c]: G[u]) {
if (dis[v] == dis[u] + 1) {
dfs(v, u, ww+(++t[c])*w[c]);
--t[c];
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; ++i) { cin >> w[i]; }
for (int i = 1; i <= m; ++i) {
int u, v, c;
cin >> u >> v >> c;
G[u].push_back( {v,c} );
G[v].push_back( {u,c} );
}
Dijkstra();
for (int i = 1; i <= n; ++i) { ans[i] = inf; }
dfs(1, 0, 0);
for (int i = 2; i <= n; ++i) { cout << ans[i] << endl; }
}
gym105386J. The Quest for El Dorado
记现在正在使用第 \(r\) 张车票,已经行驶的距离为 \(d\),定义距离为二元组 \((r,d)\)。原问题等价于求点 \(1\) 到各点的最短路是否存在。
记第 \(i\) 张车票为 \(tic[i]\)。设 \(u\) 点的最短路为 \((r,d)\),经过一条边 \((u,v,c,l)\) 时,如果 \(c\ne tic[i].a\) 或者 \(d+l>tic[i].b\),那么需要换一张车票,\(v\) 点距离更新为 \((r',l)\);否则继续使用原来的车票,\(v\) 点距离更新为 \((r,d+l)\)。
考虑如何维护 \(r'\)。\(r'\) 需要同时满足三个条件
记 \(rk[a][j]=i\) 表示第 \(j\) 张 \(a\) 公司的车票为 \(tic[i]\),在 \(rk[a]\) 中二分找到第一个 \(rk[a][y]>r\) 的 \(y\)。
记 \(val[a][j]=b\) 表示第 \(j\) 张 \(a\) 公司的车票可以行驶 \(b\) 的距离,在 \(val[a]\) 中二分找到第一个 \([y,z]\) 最大值大于等于 \(l\) 的 \(z\),则 \(r'=rk[a][z]\)。这一步可以用 ST 表维护。
最终复杂度为 \(O(m(\log n+\log k))\)。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=5e5+5;
int n, m, k;
vector <array<int,3>> G[N];
template <typename T>
struct ST {
int n=0, I=0;
vector<int> Log;
vector<vector<T>> st;
ST() { }
ST(const vector<T>& a) {
n = a.size();
Log.assign(n+1, 0);
for (int i = 2; i <= n; ++i) { I=Log[i]=Log[i/2]+1; }
st.assign(I+1, vector<T>(n));
copy(a.begin(), a.end(), st[0].begin());
for (int i = 1; i <= I; ++i) {
for (int j = 0; j+(1<<(i-1)) < n; ++j) {
st[i][j] = max( st[i-1][j], st[i-1][j+(1<<(i-1))] );
}
}
}
T query(int l, int r) { // 注意下标从 0 开始
int s = Log[r-l+1];
return max( st[s][l], st[s][r-(1<<s)+1] );
}
int find(int l, T x) { // 第一个区间 [l,r] 最值大于等于 x 的 r
if (l >= n) { return -1; }
int rl=l-1, rr=n;
while (rl != rr-1) {
int mid = (rl + rr) >> 1;
if (query(l, mid) >= x) { rr = mid; }
else { rl = mid; }
}
if (rr < n) { return rr; }
return -1;
}
};
void solve()
{
cin >> n >> m >> k;
for (int i = 1; i <= n; ++i) { G[i].clear(); }
for (int i = 1; i <= m; ++i) {
int u, v, c, l;
cin >> u >> v >> c >> l;
G[u].push_back( {v,c,l} );
G[v].push_back( {u,c,l} );
}
vector <ST<int>> st(m+1);
vector rk(m+1, vector<int>());
vector val(m+1, vector<int>());
vector <pii> tic(k+1);
for (int i = 1; i <= k; ++i) {
int a, b;
cin >> a >> b;
tic[i] = { a, b };
rk[a].push_back(i);
val[a].push_back(b);
}
for (int i = 1; i <= m; ++i) { st[i] = ST<int>(val[i]); }
vector<bool> vis(n+1, false);
priority_queue<array<int,3>, vector<array<int,3>>, greater<array<int,3>>> q;
auto update = [&](int r, int d, int u) {
vis[u] = true;
for (auto [v,c,l]: G[u]) {
if (vis[v]) { continue; }
if (c != tic[r].first || d+l > tic[r].second) {
int y = upper_bound(rk[c].begin(), rk[c].end(), r)-rk[c].begin();
int z = st[c].find(y, l);
if (z != -1) {
q.push( { rk[c][z], l, v } );
}
} else {
q.push( { r, d+l, v } );
}
}
};
update(0, 0, 1);
while (!q.empty()) {
auto [r, d, u] = q.top(); q.pop();
if (!vis[u]) { update(r, d, u); }
}
for (int i = 1; i <= n; ++i) { cout << int(vis[i]); }
cout << "\n";
}
int main()
{
cin.tie(nullptr)->sync_with_stdio(false);
int t; cin >> t;
while (t--) { solve(); }
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号