P10493 Bloxorz ||

你以为的解法：数学找规律 ×
实际上的解法：数学 + bfs搜索 √

题目大意：

如果想要练习bfs，可以查看其原题 Bloxorz |.

题目的背景续接 Bloxorz |，在一的主角(没错，就是屏幕面前的蒟蒻)被打败后，一怒之下，
向我们发起了新的问题：如果给定方块的坐标，在无限大的棋盘上，需要至少多少步才可以到达？

题目范围:终点坐标始终为 \((0,0)\) ，方块坐标 \(|x|,|y| \le 10^9\) .且题目有多组数据最多不超过100组。

注：与一代不同的是，方块起始的状态虽然仍是一个1x2的方块，但是会以 "竖立(U)","与x轴平行-横躺(V)","与y轴平行-竖躺(H)" 三种形态其中一种为初始状态.
详细说明，题目里也说了横躺和竖躺的另外一个格子坐标为 \((x + 1,y)\) 和 \((x,y + 1)\) .

题目解法：

这是一只蒟蒻QWQ，他在看题的第一眼便点开标签：广搜bfs。

bfs?这么大，哪来的时间模拟？肯定是个数学题QAQ，又要开始受苦了...

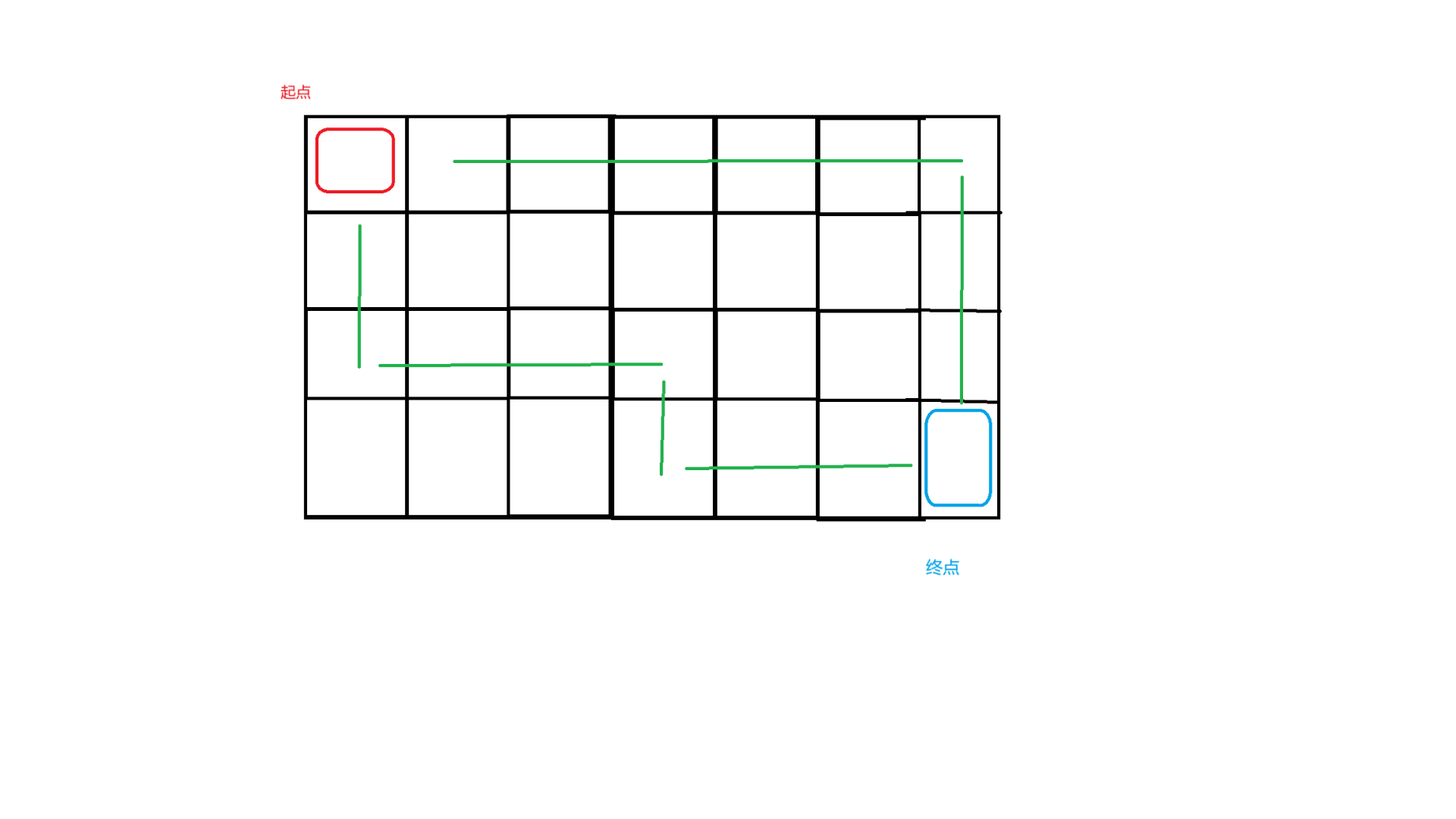
在漫长的折磨中，蒟蒻画出了这样的一个图：

欸？为什么在走了一定格子数量后由回到了原始状态？
计算ing...
好像只要差距为3的倍数就可以！那是不是其他的也是这个规律，再去找找...

只剩下一堆草稿纸和一只悲伤的蒟蒻QAQ...

题目自身规律发现并不难，关键是怎么将未知的情况转为已知的情况。
也就是说，是否任意情况下，都能走到与终点坐标差为3的倍数的格子。

这点好说，既然题目没说走不到的情况，那么就一定能走到.

是的，这点没错，但没有证明.这点也很好证。对于处于树立状态的方块，一定能到自己周围的四个格子，像这样：

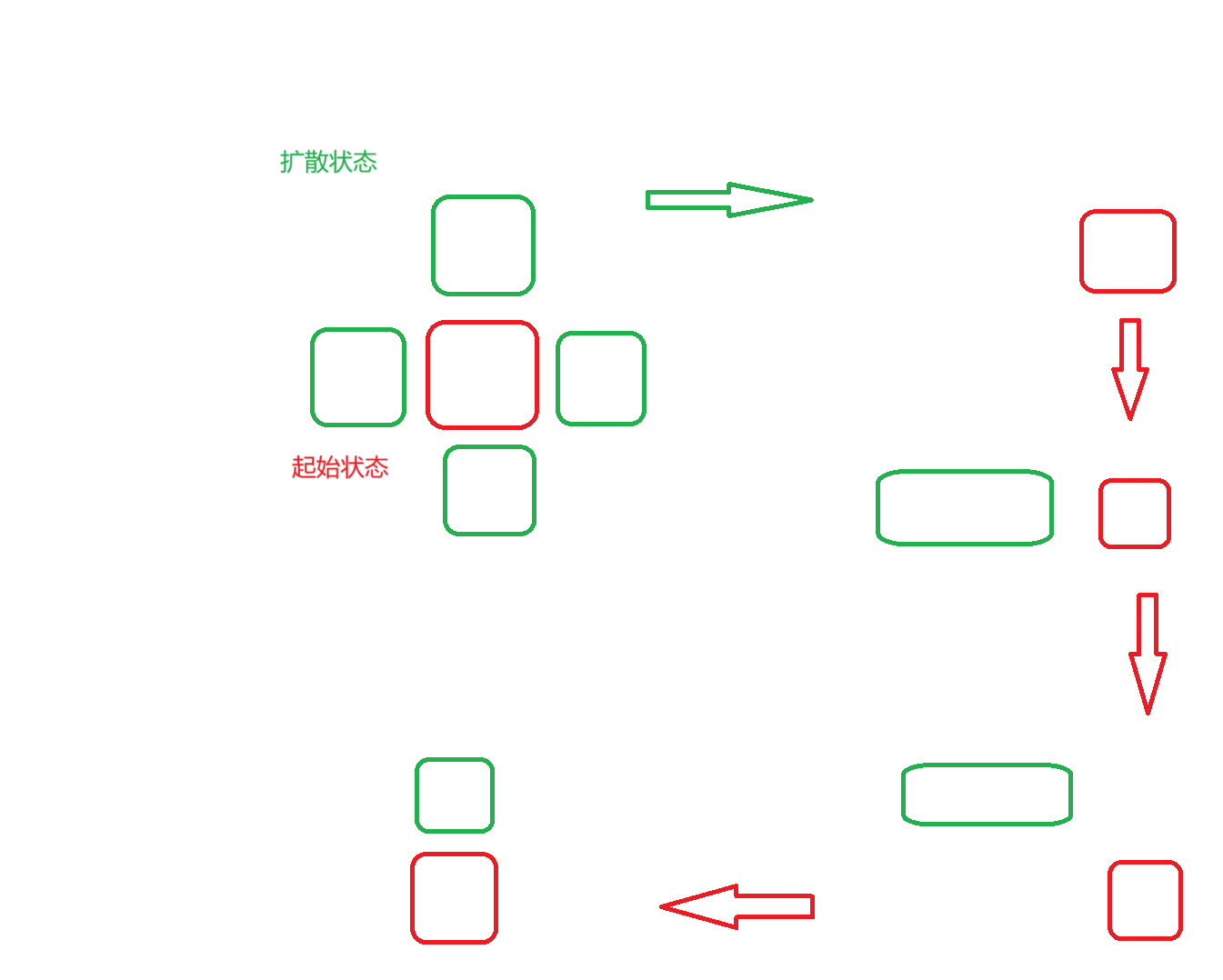
以此类推，根据归纳法，得到只要是能到达的格子，都一定能向四周扩散一个格子，这样便能推广到无限个格子。粗略的证明便完成了.

虽然看起来没什么用，但也告诉了我们任意情况一定能到达符合条件的那个点，而找寻的过程，便是搜索的事了。

我们只需搜索三格以内的所有状态，为什么是三个格？取余三的结果只有0,1,2.每个格子各占一个数值，
根据鸽巢原理，三格之内必然有一个为0的，因此只用搜三格之内.

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
struct node{
	int x, y;
    int direction;
};
char c;
int fx,fy;
int d[15][15][3];
int dx[3][4] = {{-2,1,0,0},{-1,1,0,0},{-1,2,0,0}};
int dy[3][4] = {{0,0,-2,1},{0,0,-1,2},{0,0,-1,1}};
int dd[3][4] = {{2,2,1,1},{1,1,0,0},{0,0,2,2}};
void bfs(int x, int y, int z){
	memset(d,-1,sizeof(d));
	d[x][y][z] = 0;
	queue<node> q;
	q.push({x, y, z});
	int ans = 1e10;
	while (q.size()){
		auto t = q.front();
		q.pop();
		int x = t.x, y = t.y, z = t.direction;
		if (x % 3 == 0 && y % 3 == 0 && z == 0){
			int nx = fx + x - 3, ny =fy + y - 3;
			int xd = nx / 3 * 2, yd = ny / 3 * 2;
			if (xd < 0 || yd < 0) continue;
			ans = min(ans, d[x][y][z] + xd + yd);
		}
		for (int i = 0; i < 4; i++){
			int a = x + dx[z][i];
			int b = y + dy[z][i];
			int _direction = dd[z][i];
			if (a < 0 || a >= 15 || b < 0 || b >= 15) continue;
			if (d[a][b][_direction] == -1){
				d[a][b][_direction] = d[x][y][z] + 1;
				q.push({a, b, _direction});
			}
		}
	}
    cout<<ans<<'\n';
    return
}
signed main(){
	while (cin >> c >> fx >>fy && c != EOF){
		int z;
		if (c == 'U'){z = 0;
        }else if (c == 'H'){z = 1;
        }else z = 2;
		int sx = fx % 3 + 3;
		int sy = fy % 3 + 3;
        bfs(sx, sy, z);
	}
	return 0;
}

在结尾感谢这篇文章给了我思路，使我想写一篇博客记录一下，也是第一次在洛谷交题解，管理员求过！QAQ

谢谢！