【Trick】slope trick

斯鲁普特瑞克怎么你了？

不要看到斜率就只会斜率优化，你要学会斯鲁普特瑞克。

slope trick 是一类用于维护下凸的dp函数的技巧（通常是下凸的分段一次函数）。如同所有的技巧一般，slope trick也有自己鲜明的特征，先来看一道例题。

CF713C Sonya and Problem Wihtout a Legend

给定一个有 $n$ 个正整数的数组，一次操作中，可以把任意一个元素加一或减一。（元素可被减至负数或 $0$），求使得原序列严格递增的求最小操作次数。

我们设 $f_{i,j}$ 表示考虑到第 $i$ 个数，它最终改变为 $j$ 的最小操作数。

很容易列出转移式子：

$$
f_{i,j}=\min \limits_{k=1}^{k<j}f_{i-1,k}+|a_i-j|
$$

看到转移柿子里存在绝对值函数，考虑用 slope trick 维护。先简单用数学归纳法证明下 $f_i$ 是个下凸函数。

假设 $f_{i-1}$ 长这样：

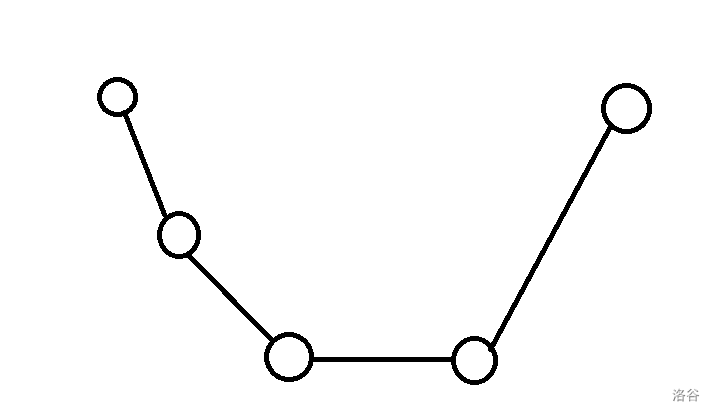
取 min 之后长这样：

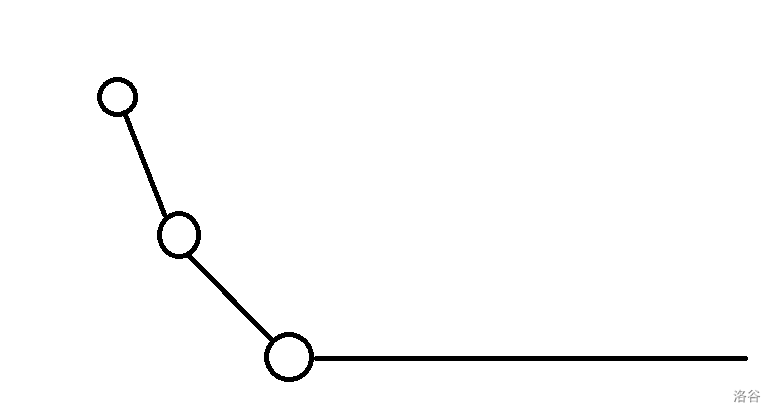
绝对值函数也是下凸函数，显然两个下凸函数加在一起还是下凸函数。

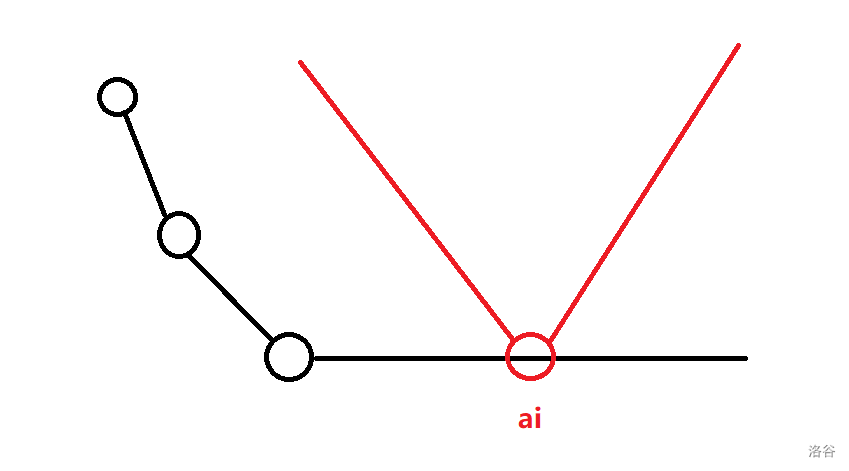
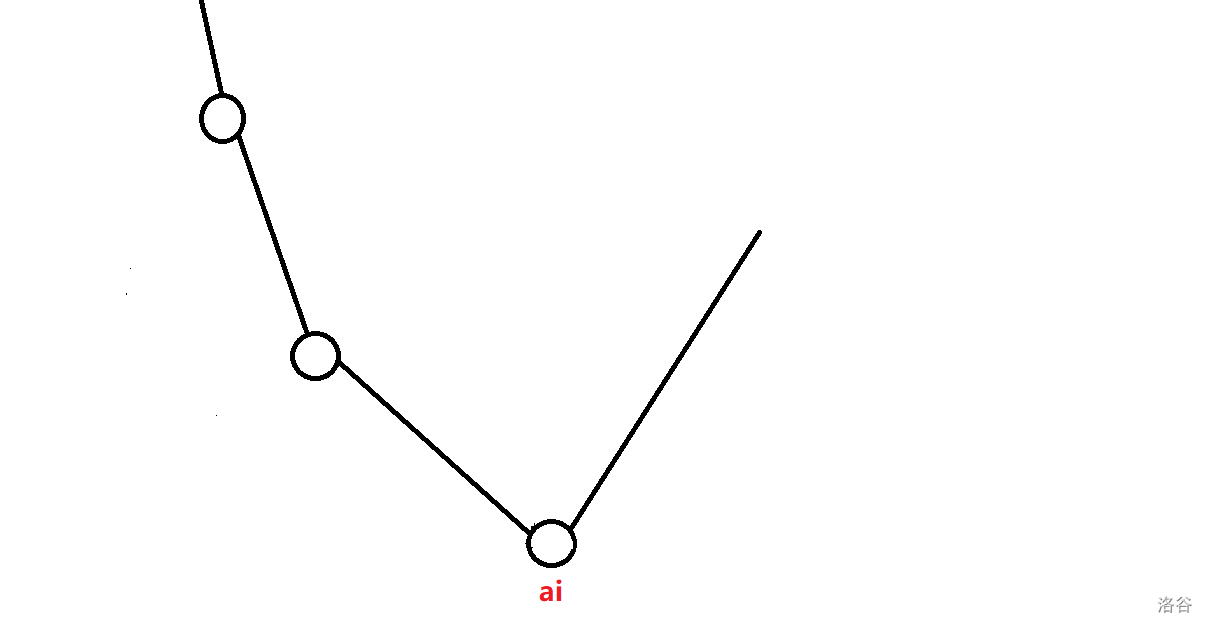
函数上有很多分界点，函数在经过分界点的时候斜率会加一，因此我们可以通过维护分界点来维护整个函数。

回到这一题，我们考虑使用一个大根堆来维护所有分界点，其中堆顶是当前
dp 函数的最低点（最低点右边的分界点在每次 dp 转移的时候都将被删除，因此没必要维护）。

现在考虑加一个绝对值函数 $|a_i-j|$，显然 $a_i$ 左边的部分斜率减一，右边的部分斜率加一，分两种情况讨论：

• $a_i$ 在当前最低点的右边，此时最低点右移到 $a_i$ 的位置，而最低点对应的 dp 值不变，并将一个 $a_i$ 放进堆中（左边的斜率减一，右边的斜率虽然加一但在之后的转移中会被推平，因此斜率变化从负一到零，加入一个 $a_i$）。

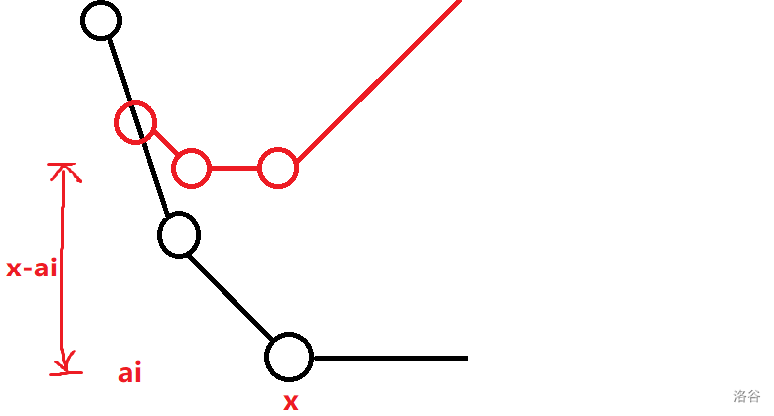
• $a_i$ 在当前最低点的左边，假设当前最低点为 $x$ ，先将两个 $a_i$ 放进堆中，此时最低点左移至堆中次大值的位置，最低点对应的 dp 值将会加上 $x-a_i$ （此时 $a_i$ 左边斜率减一而右边斜率加一，斜率变化从负一到一，因此加入两个 $a_i$）。

代码也及其好写：

#include<bits/stdc++.h>
#define int long long
using namespace std;
priority_queue<int> q;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
int n,ans;
signed main()
{
	n=read();
	for(int i=1; i<=n; i++) {
		int tmp=read()-i;
		q.push(tmp);
		if(tmp<q.top()) {
			ans+=q.top()-tmp;
			q.pop();
		}
	}
	printf("%lld",ans);
	return 0;
}

• 未完