原题回顾:在4x4方格表中选四个方格,要求每行每列恰有一个方格被选中,问四个数字之和的最大值。
| 11 | 21 | 31 | 40 |
| 12 | 22 | 33 | 42 |
| 13 | 22 | 33 | 43 |
| 15 | 24 | 34 | 44 |
Solution 1 暴力枚举
时间复杂度:O(n!)
枚举法在这里不过多提及,应该是考场上部分人的复杂且有效的方式解题。本文重点在下面。
Solution 2 状压DP
时间复杂度:O(n²2ⁿ)
该表格用a[i][j]存储。
确定状态:
定义dp[i][j]为当选取第i列,已选择的方案状压值为j时的最大值(不是所有有序对(i,j)都具有意义)。
至于状压值是什么:选取第一列那么状压值+2,选取第二列状压值+4,选取第三列状压值+8,选取第四列状压值+16;例如,状压值是18那么18=16+2,此时i=2,已选择的列数是第一列和第四列。
不难证明,对于任意一个状压值,由此计算出的选择的列的方案唯一。
初状态:
a[1][k]的所有数字都移入dp[1][1<<k]中。
状态转移方程:
当dp[i][j]非零时,有
dp[i+1][(1<<k)|j]=max(dp[i+1][(1<<k)|j],dp[i][j]+a[i+1][k]);
其中i为选择的行数,k为此时的列数。
Code:
#include<bits/stdc++.h>
using namespace std;
int n;
int a[5][5],dp[5][34];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
dp[1][1<<i]=a[1][i];
for(int i=1;i<=n-1;i++)
for(int k=1;k<=n;k++)
for(int j=1;j<=(1<<(n+1))-1;j++)
if(dp[i][j]&&(1<<k)|j>j)
dp[i+1][(1<<k)|j]=max(dp[i+1][(1<<k)|j],dp[i][j]+a[i+1][k]);
cout<<dp[n][(1<<(n+1))-2];
return 0;
}
在顺次输入
4
11
21
31
40
12
22
33
42
13
22
33
43
15
24
34
44
时输出
112
Solution 3 二分图最大权(完美)匹配-KM算法
时间复杂度:O(n³)
这个方法就有意思了,这道题是怎么跟二分图最大权匹配联系到一起的呢?
首先观察这个表格像不像邻接矩阵?
将二分图划分成两个区域,那么表格中的a[i][j]是否可以表示成区域I的i号点连接区域II的j号点,边权为a[i][j]呢?
所以说,我们可以得到以下的二分图:
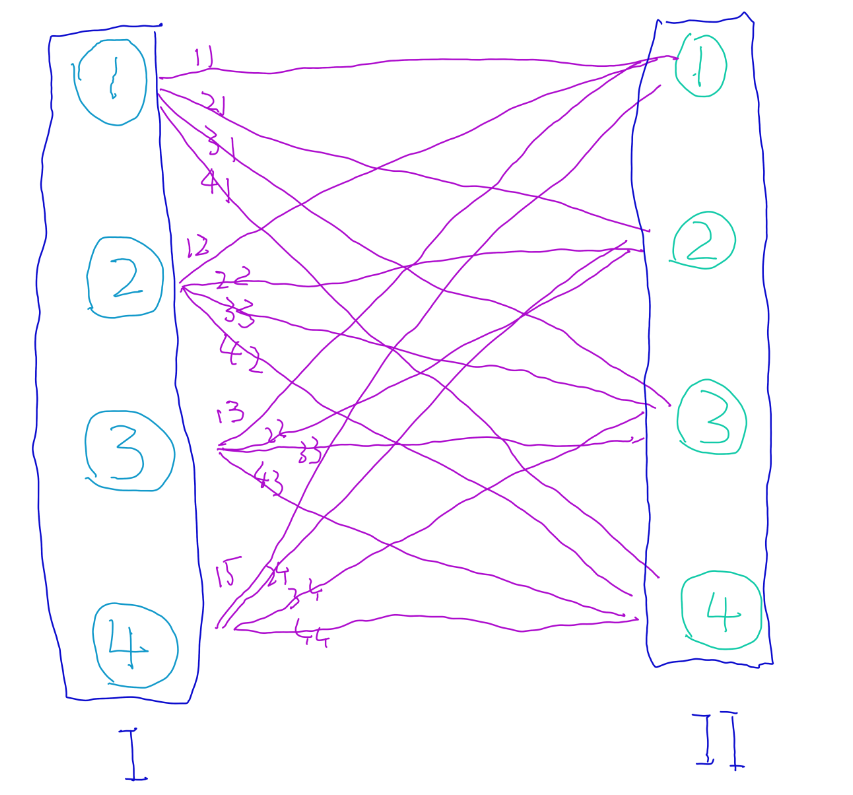
丑图致歉,就是这么个意思qwq。
i值代表区域I,j值代表区域II,那么根据匹配的定义(设G为二分图,G的子图M中任意两边都没有公共节点,称M是G的一组匹配),这幅图的最大全完美匹配值就是本题答案。
Code:
#include<bits/stdc++.h>
using namespace std;
int M;
const int maxN=403;
struct KM
{
int mp[maxN][maxN],linkx[maxN],linky[maxN],N;
bool visx[maxN],visy[maxN];
int que[maxN<<1],top,fail,pre[maxN];
int hx[maxN],hy[maxN],slk[maxN];
inline int check(int i)
{
visx[i]=true;
if(linkx[i])
{
que[fail++]=linkx[i];
return visy[linkx[i]]=true;
}
while(i)
{
linkx[i]=pre[i];
swap(i,linky[pre[i]]);
}
return 0;
}
void bfs(int s)
{
for(int i=1;i<=N;i++)
{
slk[i]=INT_MAX;
visx[i]=visy[i]=false;
}
top=0,fail=1;
que[0]=s;
visy[s]=true;
while(1)
{
int d;
while(top<fail)
{
for(int i=1,j=que[top++];i<=N;i++)
{
if(!visx[i]&&slk[i]>=(d=hx[i]+hy[j]-mp[i][j]))
{
pre[i]=j;
if(d)
slk[i]=d;
else if(!check(i))
return;
}
}
}
d=INT_MAX;
for(int i=1;i<=N;i++)
if(!visx[i]&&slk[i]<d)
d=slk[i];
for(int i=1;i<=N;i++)
{
if(visx[i])
hx[i]+=d;
else
slk[i]-=d;
if(visy[i])
hy[i]-=d;
}
for(int i=1;i<=N;i++)
if(!visx[i]&&!slk[i]&&!check(i))
return;
}
}
void init()
{
for(int i=1;i<=N;i++)
{
linkx[i]=linky[i]=0;
visy[i]=false;
for(int i=1;i<=N;i++)
{
hx[i]=0;
for(int j=1;j<=N;j++)
hx[i]=max(hx[i],mp[i][j]);
}
}
}
}km;
int main()
{
cin>>km.N>>M;
for(int i=1,u,v,w;i<=M;i++)
{
cin>>u>>v>>w;
km.mp[u][v]=w;
}
int ans=0;
km.init();
for(int i=1;i<=km.N;i++)
km.bfs(i);
for(int i=1;i<=km.N;i++)
ans+=km.mp[i][km.linkx[i]];
cout<<ans;
return 0;
}
在输入
4 16
1 1 11
1 2 21
1 3 31
1 4 40
2 1 12
2 2 22
2 3 33
2 4 42
3 1 13
3 2 22
3 3 33
3 4 43
4 1 15
4 2 24
4 3 34
4 4 44
时输出
112

