CMU Convex Optimization(凸优化)笔记1--凸集和凸函数

CMU凸优化笔记--凸集和凸函数

结束了一段时间的学习任务，于是打算做个总结。主要内容都是基于CMU的Ryan Tibshirani开设的Convex Optimization课程做的笔记。这里只摘了部分内容做了笔记，很感谢Ryan Tibshirani在官网中所作的课程内容开源。也很感谢韩龙飞在CMU凸优化课程中的中文笔记，我在其基础上做了大量的内容参考。才疏学浅，忘不吝赐教。

1、凸集合

1.1 基本概念

定义：给定一个集合$C \subseteq \mathbb{R}^n $,满足下列条件则称为凸集

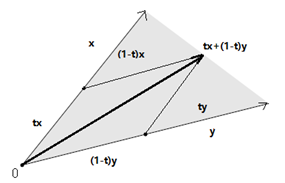
$x,y \in C  \Rightarrow tx+(1-t)y \in C $ 对于任意的 $ 0 \leq t \leq 1$

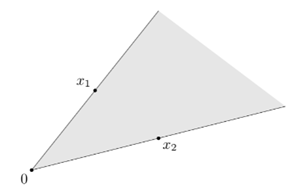
直观上看，可以利用下图帮助理解，假定我们的变量在二维空间中，$x,y$为二维空间变量，黑体线代表的向量为$tx+(1-t)y$，$t$取值范围为$[0,1]$，那么无论t怎么变化，向量$tx+(1-t)y$总会落在$x$和$y$张成的集合空间中。

那么从定义出发，我们也能知道非凸集的情况，下图左侧为凸集，右图为非凸集

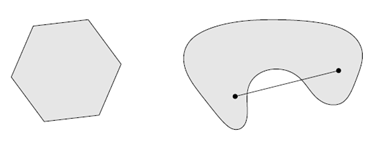
一句话来概括凸集就是集合内任意两点间连线依旧在集合内。

1.2  凸集简单例子

• 凸包(convex hull)：给定集合内的任意$k$个元素$x_1,...,x_k \in \mathbb{R}^n$,任意的线性组合形式：

$\theta_1 x_1+...+\theta_k x_k,\theta_i \leq,i=1,...,k$ 并且$ \sum_{i=1}^{k}\theta_i=1$。称之为集合的convex hull,表示为$conv(C)$。convex hull总是凸的。可以直观认为凸包就是最外围的元素所围成的集合外壳，下图是两个凸包的例子：

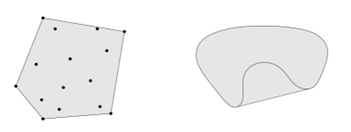
• 空集、点、线都是凸集合
• 范数球（Norm ball）: 半径为$r$的范数球为：$\left \{x:||x|| \leq r \right \}$
• 超平面（Hyperplane）: 给定任意$a,b$ ,$\left \{x:a^Tx=b \right \}$
• 半空间（Half space）: $\left \{x:a^Tx \leq b \right \}$
• 仿射空间(Affine space):$\left \{x:Ax = b \right \}$
• 多面体(Polyhedron):$\left \{x:Ax \leq b \right \}$，下图为多面体

 

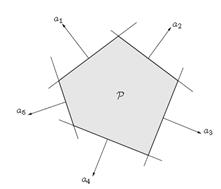
Note:集合$\left \{x:Ax \leq b,Cx=d \right\}$也是一个Polyhedron吗？

Answer:是的。因为对于任意的$Cx=d$，都可写成$Cx \leq d$ 与$-Cx \leq -d$,这样就和$Ax \leq b $形式一致。

1.3  锥（Cone）：

定义：给定$C \in \mathbb{R}^n $，满足$x \in C \Rightarrow tx\in C$ 对于任意$ t\geq 0$称之为锥。

凸锥（convex cone）：$x_1,x_2 \in C \Rightarrow t_1 x_1+t_2 x_2 \in C $,对于任意$ t_1,t_2 \geq 0$都成立，那么称集合$C$为凸锥。显然凸锥是锥的一种。

例子：

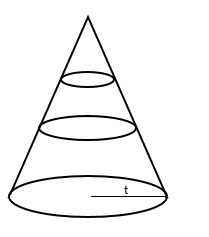
范数锥(Norm cone):$\left \{(x,t):||x|| \leq t \right \}$，对于一范数和二范数成立。下图取定不同的$t$做出了三维情况下的图：

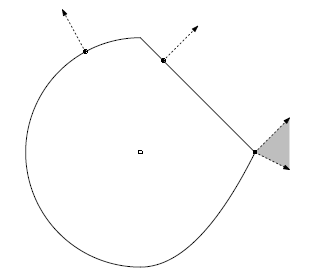
正规锥(Normal cone):给定任意集合$C$，集合内任意一点$x \in C$,定义：

$\mathbb{N}_c(x)=\left \{g:g^Tx \geq g^Ty ,for \quad any \quad y \in C \right \}$

其含义是指Normal cone中的点与集合$C$内的点的内积永远大于集合内任意点与Normal cone内点的内积。如下图所示：

 

1.4  凸集的一些特性

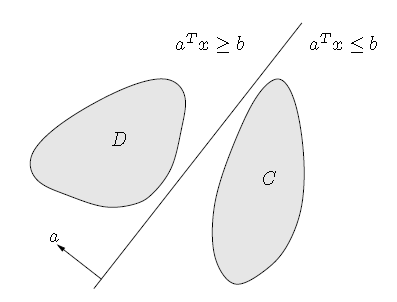
•  可分离超平面理论（Separating hyperplane theorem）：两个不相交的凸集总存在一个超平面能将两者分离，如果$C \bigcap D =  \varnothing $,那么总存在着$a,b$使得有:

$C \subseteq \left \{x:a^Tx \leq b \right \}$ ,$D \subseteq \left \{x:x^T \geq b \right \}$。如下图所示：

• 支撑超平面理论(Supporting hyperplane theorem):凸集边界上的一点必然存在一个支撑超平面穿过该点，即如果$C$都是非空凸集，$ x_0 \in $ bd$(C) $，那么必然存在一个超平面$a$，使得, $C \subseteq \left \{x:a^Tx \leq a^T x_0 \right \}$。如下图：

1.5  保凸操作

• 集合交（Intersection）：任何凸集之交产生的集合依旧是凸集。
• 缩放和平移（Scaling and translation）：假设$C$为凸集，那么$aC+b=\left \{ax+b:x \in C \right \}$对于任意$a,b$也是凸的。
• 仿射映射与预映射(Affine images and preimages)：如果$f(x)=Ax+b$是凸集，那么$f(C)=\left \{f(c):x \in C \right\}$也是凸集，如果$D$为凸集，那么$f^(-1)(D)=\left \{x:f(x) \in D \right \}$也是凸的。

1.6  凸集与保凸操作相关例子

条件概率集合(conditional probability set)：$U,V$分别为$\left \{1,...,n\right \}$与$\left \{1,...,m\right \}$上的两个随机变量集合。$ C \subseteq \mathbb{R}^{nm} $为$U,V$的联合分布集合。对于每个$p \in C$，定义联合概率分布 $p_{ij} = \mathbb{P}(U=i,V=j)$。D为对应的条件概率分布，对于每个$q \in D$定义 $q_{ij}=\mathbb{P}(U=i|V=j)$。假定$C$为凸集，那么D一定为凸集。简单证明可用保凸操作中的Affine images and preimages，$D=\{q\in\mathbb{R}^{nm}:q_{ij}={\textstyle\frac{p_{ij}}{\textstyle\overset n{\underset{k=1}{\sum p_{kj}}}}}\}$

2 、凸函数 

2.1 基本概念

 定义：给定映射$f:\mathbb{R}^n \rightarrow \mathbb{R}$ 并且 dom$(f) \subseteq \mathbb{R}^n$为凸集，那么

$f(tx+(1-t)y) \leq tf(x)+(1-t)f(y)$ 对于任意 $0 \leq t \leq 1$，且 任意$x,y \in dom(f)$。如下图：

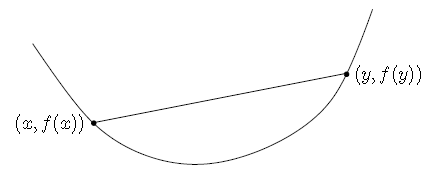
从上图可以看出，$f$的函数值总是位于连接$f(x)$和$f(y)$之间的直线下方。

Note:

• 严格凸(Strictly convex):对于任意$x \neq y$,且$0<t<1$,有$f(tx+(1-t)y)<tf(x)+(1-t)f(y)$。简而言之，就是$f$比线性函数要更弯曲
• 强凸(Strongly convex):对于参数$m>0$:$f-\frac{m}{2}||x||^2_2$依旧是一个凸函数。简而言之就是$f$要比一般的二次函数要弯曲。
• 强凸 $\Rightarrow$ 严格凸 $\Rightarrow$ 凸

2.2 凸函数例子

• 单变量函数：

例如指数函数$e^{ax} $对于任意a都是凸的，幂函数$x^a$在$a\geq 1 或 a \leq 0$的时候为凸，当$0 \leq a \leq 1$的时候非凸，对数函数$log x$是非凸函数

• 仿射函数(Affine function):

$a^Tx+b$既是凸函数又是非凸函数

• 二次函数(Quadratic function)：

$\frac{1}{2}x^TQx+b^Tx+c$当$Q \succeq 0$（半正定）的时候为凸

• 最小平方损失函数（Least squares loss）:

$||y-Ax||_2^2$总是凸的，因为展开后的$A^TA$总是半正定的

• 范数(Norm)：

$||x||$的任何范数总是凸的，$\ell_p$范数定义为：$\parallel x\parallel_p=(\overset n{\underset{i=1}{\sum x_i^p}})^{1/p}$，对于任意$p\geq1$,$\parallel x\parallel _{\infty} =max|x_i|$。

谱(spectral)范数：$\parallel X \parallel _{op}=\sigma_1(X)$,

核范数（nuclear）:$||X||_{tr}=\sum_{i=1}^{r}\sigma_r(X)$。其中$\sigma_1(X)\geq...\geq\sigma(X)\geq0$为矩阵$X$的从大到小排序的奇异值。

• 指示函数(Indicator function):

如果$C$为凸，那么其指示函数为：$I_C(x)=\left\{\begin{array}{lc}0&x\in C\\\infty&x\not\in C\end{array}\right.$为凸函数。

• 最大值函数（Max function）:

$f(x)=max\left\{x_1,...,x_n\right\}$为凸函数

2.3 凸函数的一些特性

• 上镜特性(Epigraph characterization):函数$f$为凸函数当且仅当其上镜图$epi(f)=\left \{(x,t)\in dom(f)\times \mathbb{R}:f(x)\leq t\right\}$为凸集，如下图：

• 一阶特性(First-order characterization):假设$f$处处可微，那么$f$为凸函数当且仅当$dom(f)$为凸，并且有：$f(y)\geq f(x)+\nabla f(x)^T(y-x)$对于所有$x,y\in dom(f)$。

Note:如何证明凸函数的一阶特性？

Answer:从凸函数定义出发，$f(ty+(1-t)x) \leq tf(y)+(1-t)f(x) \quad \Rightarrow \quad \\ f(t(y-x)+x)+f(x))\leq t(f(y)-f(x))+f(x) \quad \Rightarrow \quad \\ \frac{f(t(y-x)+x)-f(x)}{t(y-x)}\leq frac{f(y)-f(x)}{y-x} \quad \Rightarrow \quad \\ \lim_{t\rightarrow0} \frac{f(t(y-x)+x)-f(x)}{t(y-x)}=\nabla f(x) \quad \Rightarrow \quad  \\ \nabla f(x)(y-x) \leq f(y)-f(x) \quad \Rightarrow \quad \\ f(y) \geq f(x)+\nabla f(x)(y-x)$

• 二阶特性：如果函数二阶可微分，则$f$为凸函数当且仅当$dom(f)$为凸，且对于所有$x \in dom(f)$ 都有$\nabla^2f(x)\succeq0$
• Jensen不等式：假若$f$为凸，并且$X$由$dom(f)$所支持的随机变量，则有$f(\mathbb{E}[x])\leq\mathbb{E}[f(x)]$

 2.4保凸操作

• 非负线性组合

$f_1,...,f_m$均为凸函数，那么对任意$a_1,...a_m\geq0$均有$a_1f_1+...+a_mf_m$为凸。

• 逐点最大化

如果$f_s$对于任意$s\in S$均为凸，那么$f(x)=max_{s\in S}f_s(x)$是凸函数。

• 部分最小化

如果$g(x,y)$在任意$x,y$处为凸函数，并且$C$是凸的，那么$f(x)=min_{y\in C}g(x,y)$为凸函数。

2.5 证明凸函数例子

对数求和函数(Log-sum-exp function)：“soft max”函数：对于给定$a_i,b_i,i=1,...,k$，$g(x)=log(\sum_{i=1}^{k}e^{a_i^Tx+b_i})$。其光滑近似为$max_{i=1,...,k}(a_i^Tx+b_i)$。

那么为了证明凸函数，首先我们知道仿射函数均是凸函数，并且对于求和函数可以看成是$f(x)=log(\sum_{i=1}^{n}e^{x_i})$与$h(x)=a_i^Tx+b_i$的复合函数。因此只需要证明$f(x)$为凸函数即可。

$\nabla _i f(x)=\frac{e^{x_i}}{\sum_{l=1}{n}e^{x_l}}\\$

$\nabla_{ij}^{2}f(x)=\frac{e^{x_i}}{\sum_{l=1}{n}}1\{i=j\}-\frac{e^{x_i}e^{x_j}}{(\sum_{l=1}^{n}e^{x_l})^2}\\$

将上式重写为$\nabla^2f(x)=diag(z)-zz^T$,其中$z_i=e^{x_i}/(\sum_{l=1}^{n}e^{x_l})$。这是一个对角占优矩阵，因此是半正定矩阵，因此满足二阶性质。原式为凸函数得证。