数据结构与算法（7）--树和二叉树

Ch7 树和二叉树

---

0x01 树

---

树的定义

树是n个结点的有限集，当n=0时称为空树。
树其实是一种递归的实现，树的定义中还用到了树的概念。
在任意一个非空树中：
（1）有且仅有一个特定的结点：根结点（root）（根结点没有前驱结点）。
（2）当n>1时，其余结点可以分为m>0个互不相交的有限集，其中每一个集合本身又是一棵树，并且称为根的子树。
（3）根结点存在时，是唯一的，不可能同时存在多个根结点。
（4）子结点存在时，子树的个数没有限制，但它们一定互不相交。

一些术语

• 结点：由数据元素和构造数据元素之间关系的指针组成
• 结点的度：结点所拥有的子树的个数
• 叶结点：度为0的结点，也称作终端结点
• 分支结点：度不为0的结点
• 孩子结点：树中一个结点的子树的根结点
• 双亲结点：若树中某结点有孩子结点，则这个结点就称作它的孩子结点的双亲结点
• 兄弟结点：具有相同的双亲结点的结点
• 树的度：树中所有结点的度的最大值
• 结点的层次：从根结点到树中某结点所经路径上的分支数
• 树的深度：树中所有结点的层次的最大值
• 无序树：树中任意一个结点的各孩子结点之间的次序构成无关紧要的树
• 有序树：树中任意一个结点的各孩子结点有严格排列次序的树
• 森林：m（m≥0）棵树的集合。

树的表示方法

直观表示法、形式化表示法，凹入表示法。

树的操作集合

创建树，撤销树，查找树中当前结点的双亲结点，左孩子结点，右兄弟结点，遍历树等。

树的存储结构

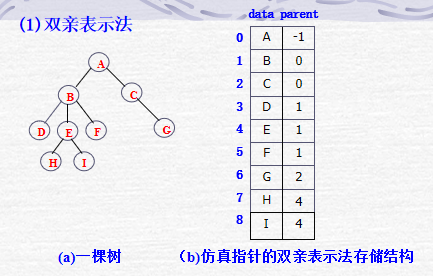
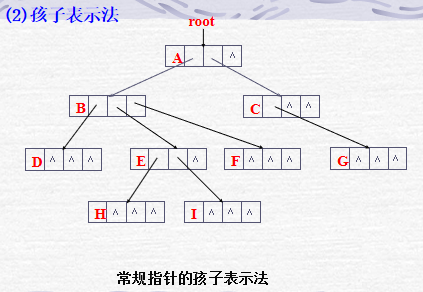
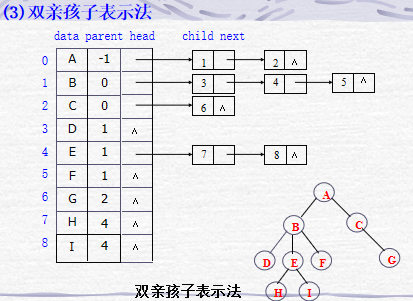
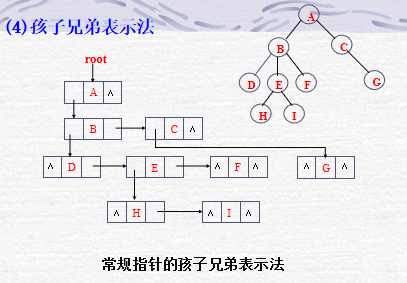
树的结点之间的逻辑关系主要有双亲-孩子关系，兄弟关系。因此，从结点之间的逻辑关系分，树的存储结构主要有：双亲表示法、孩子表示法、双亲孩子表示法和孩子兄弟表示法四种组合。

0x02 二叉树

二叉树是n≥0个结点的有限集合，该集合可以为空集（空二叉树），或者由一个根结点和两颗互不相交的分别称为根结点的左子树和右子树的二叉树组成。
二叉树特点：

• 每个结点最多只能有两颗子树
• 左子树和右子树是有顺序的，不能颠倒
• 即使某个结点只有一颗子树，也要区分左右子树。

二叉树基本形态

• 空二叉树
• 只有根结点
• 只有左子树
• 只有右子树
• 左右子树都有

特殊的二叉树

满二叉树：
在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树。（一个叶子都不少）
完全二叉树：
如果一棵深度为k，有n个结点的二叉树中各结点能够与深度为k的顺序编号的满二叉树从1到n标号的结点相对应的二叉树称为完全二叉树。（只有最后一层结点不满，且结点全部集中在左侧，允许右边缺少连续若干个结点）

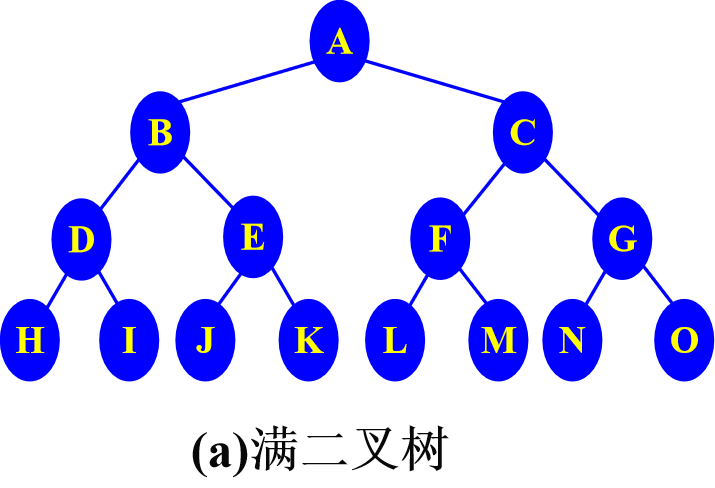
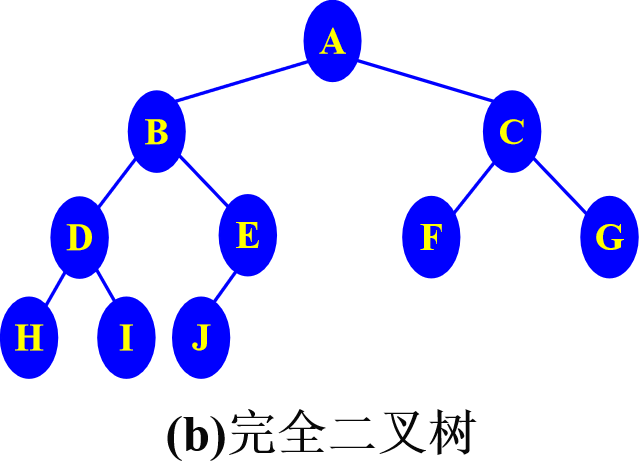
满二叉树是完全二叉树的一个特例。

二叉树的操作集合

创建二叉树、撤销二叉树、左插入结点、右插入结点、左删除子树、右删除子树、遍历二叉树。

---

二叉树的性质

---

二叉树的五种特性：
1.第i层最多有2的i次方个结点（i>=0，即从1开始计数时)
2.深度为k的二叉树最多有2的k+1次方-1个结点。（k>=-1）
3.具有n个结点的完全二叉树的深度k为向下取整的log2(n+1) + 1。
4.对有n个结点的完全二叉树中的结点从上到下，从左到右编号i(0≤i≤n），那么有：

• 如果i=0，则结点i是二叉树的根，无双亲。如果i>0，则其双亲是结点(i-1)/2(“/”表示整除）。
• 如果2i+1≥n，则结点无左孩子，否则左孩子是结点2i+1。
• 如果2i+2≥n,则结点i无右孩子，否则其右孩子是结点2i+2。

5.（补充）对于任何一颗二叉树，如果其叶子结点数为n0，度（即子结点数）为2的结点数为n2，那么有n0=n2+1。
证明：
对于分支数有B=n-1=n2*2+n1 =》n = n2*2+n1 + 1
对于结点数，又有n = n2+n1+n0
综上得到结论n0=n2+1。

二叉树的存储结构

• 顺序存储结构
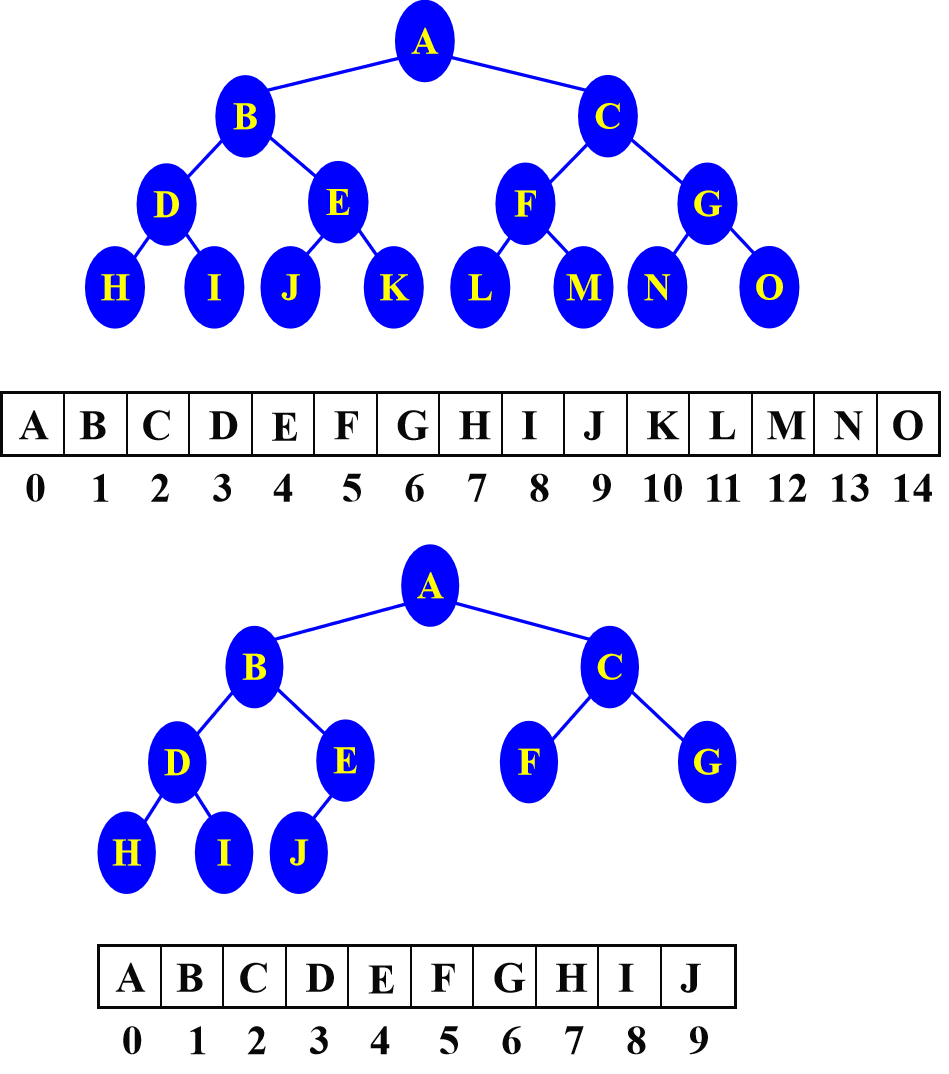
  完全二叉树的结点可按从上至下和从左至右的次序存储在一维数组中，其结点之间的关系可由公式计算得到。
  
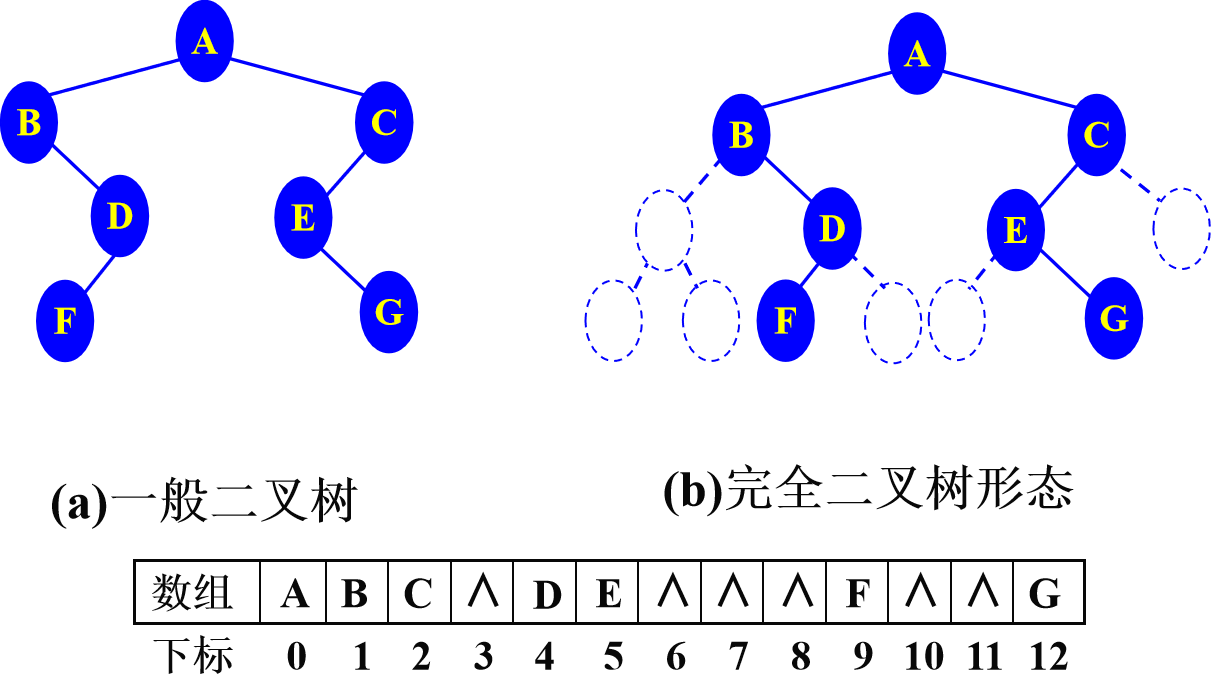
  一般的非完全二叉树，则可以通过添加空结点方式，进而用顺序存储结构存储。
  

• 链式存储结构

最常用的是二叉链，每个结点包含三个域，分别是数据域，左孩子指针域，右孩子指针域。（也分为带头结点和不带头结点）。

• 仿真指针存储结构

用数组存储二叉树中的结点，数组中每个结点除数据元素域外，再增加仿真指针域用于仿真常规指针建立二叉树中结点之间的关系。如下图。

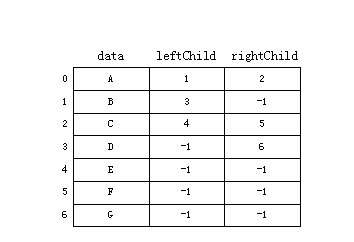
二叉树的四种遍历方式

若规定D,L,R分别代表“访问根结点”、“遍历根结点的左子树”和“遍历根结点的右子树”，根据遍历算法对访问根结点处理的位置有前序遍历，中序遍历，后序遍历。若二叉树为空，则算法结束。

• 前序遍历（DLR）：先根再左再右
• 中序遍历（LDR）：先左再跟再右
• 后序遍历（LRD）：先左再右再根

用二叉树表示算术表达式：

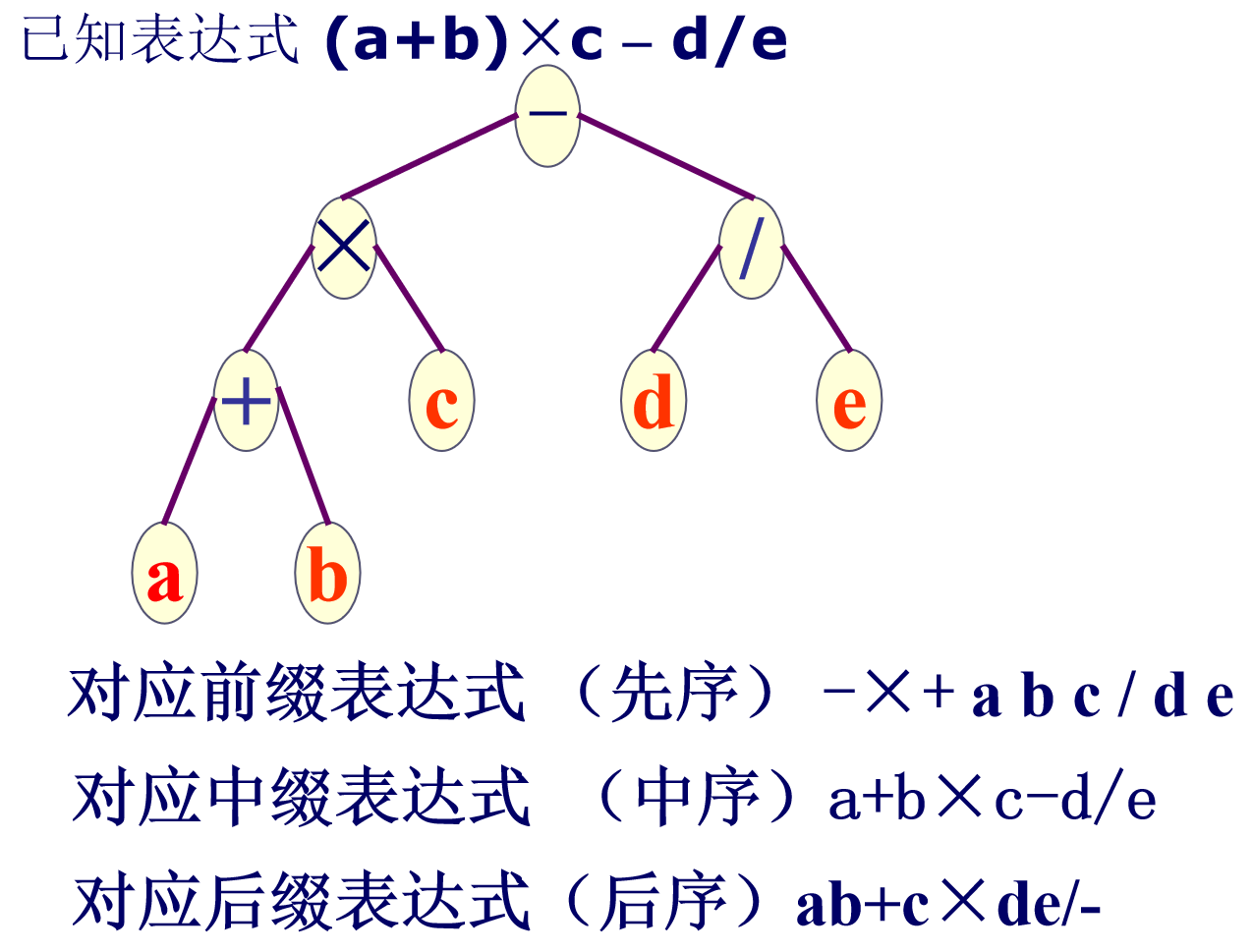
• 层序遍历
  按二叉树的层序次序（即从根结点层至叶结点层），同一层中按先左子树再右子树的次序遍历二叉树。
  算法如下：

（1）初始化设置一个队列；
（2）把根结点指针入队列；
（3）当队列非空时，循环执行步骤（3.a）到步骤（3.c）；
（3.a）出队列取得一个结点指针，访问该结点；
（3.b）若该结点的左子树非空，则将该结点的左子树指针入队列；
（3.c）若该结点的右子树非空，则将该结点的右子树指针入队列；
（4）结束。

注意：当对一个二叉树用一种特定的遍历方法来遍历时，其遍历序列一定是线性的，且是惟一的。
二叉树的遍历方法和二叉树的结构：
二叉树是非线性结构，每个结点会有零个、一个或两个孩子结点，一个二叉树的遍历序列不能决定一棵二叉树，但某些不同的遍历序列组合可以惟一确定一棵二叉树。例如给定一棵二叉树的前序遍历序列和中序遍历序列可以惟一确定一棵二叉树的结构。
重要结论：若二叉树中各结点的值均不相同，则：由二叉树的前序序列和中序序列，或由其后序序列和中序序列均能唯一地确定一棵二叉树，但由前序序列和后序序列却不一定能唯一地确定一棵二叉树。

例子：
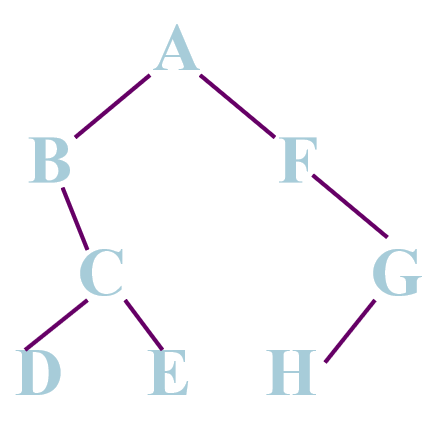
已知一棵二叉树的中序序列和后序序列分别是BDCEAFHG 和 DECBHGFA，请画出这棵二叉树。

①由后序遍历特征，根结点必在后序序列尾部（A）；
②由中序遍历特征，根结点必在其中间，而且其左部必全部是左子树子孙（BDCE），其右部必全部是右子树子孙（FHG）；
③继而，根据后序中的DECB子树可确定B为A的左孩子，根据HGF子串可确定F为A的右孩子；以此类推。

二叉树遍历的实现

template <class T>
void PreOrder(BiTreeNode<T> *t, void Visit(T item))
//使用Visit(item)函数前序遍历二叉树t
{
	if(t != NULL)
	{
		Visit(t->data);
		PreOrder(t->Left(), Visit);
		PreOrder(t->Right(), Visit);
	}
}

emplate <class T>
void InOrder(BiTreeNode<T> *t, void Visit(T item))
//使用Visit(item)函数中序遍历二叉树t
{
	if(t != NULL)
	{
		InOrder(t->Left(), Visit);
		Visit(t->data);
		InOrder(t->Right(), Visit);
	}
}


template <class T>
void PostOrder(BiTreeNode<T> *t, void Visit(T item))
//使用Visit(item)函数后序遍历二叉树t
{
	if(t != NULL)
	{
		PostOrder(t->Left(), Visit);
		PostOrder(t->Right(), Visit);
		Visit(t->data);
	}
}

二叉树遍历的应用

(1)二叉树的撤销

在释放某个结点的存储空间前必须先释放该结点左孩子结点的存储空间和右孩子结点的存储空间，因此，二叉树撤消操作必须是后序遍历的具体应用。

template <class T>
void Destroy(BiTreeNode<T> *&root)
{
	if((root) != NULL && (root)->Left() != NULL)
		Destroy(root->Left());

	if((root) != NULL && (root)->Right() != NULL)
		Destroy(root->Right());

	cout << root->data << " ";	  //此语句只是为了方便测试
	delete root;
}

(2)二叉树的打印

把二叉树逆时针旋转900，按照二叉树的凹入表示法打印二叉树。可把此函数设计成递归函数。由于把二叉树逆时针旋转900后，在屏幕上方的首先是右子树，然后是根结点，最后是左子树，所以打印二叉树算法是一种特殊的中序遍历算法的应用。

template <class T>
void PrintBiTree(BiTreeNode<T>* &root, int level)
//二叉树root第level层结点数据域值的横向显示
{	  if(root != NULL)			//如果二叉树不空
	{    //二叉树root->Right()第level+1层结点数据域值的横向显示
		PrintBiTree(root->Right(), level+1);		
		if(level != 0)							{	//走过6*(level-1)个空格
			for(int i = 0; i < 6*(level-1); i++) cout<<" ";
			cout << "  ----";		//显示横线----
		}
		cout << root->data << endl;	//显示结点的数据域值
		//二叉树root->Left()第level+1层结点数据域值的横向显示
		PrintBiTree(root->Left(), level+1);
	}
} 

(3)查找数据元素

在bt为根结点指针的二叉树中查找数据元素x，若查找到数据元素x时返回该结点的指针；若查找不到数据元素x时返回空指针。
此时可以任意顺序遍历，这里设计为先序遍历函数。

template <class T>     
BiTreeNode<T>* Search(BiTreeNode<T>* t, T x) {
	BiTreeNode<T>* p;	
	if (t == NULL) return NULL;	//空二叉树时的查找失败出口	
	if(t->data == x) return t;		//查找成功出口	
	if(t->Left() != NULL)						
	{									
		p = Search(t->Left(), x);		//在左子树查找		               
		if(p != NULL) return p;	//查找成功时结束递归过程	
	}						
	if(t->Right() != NULL)						
	{									
		p = Search(t->Right(), x);	//在右子树查找				
		if(p != NULL) return p;	//查找成功时结束递归过程	
	}						
	return NULL;				//查找失败出口	                  
}

非递归的二叉树遍历算法

所有递归算法都可以借助堆栈转换成循环结构的非递归算法，通常有两种方法：一种方法是形式化模拟转换，另一种方法是根据要求解问题的特点设计借助堆栈的循环结构算法。
非递归的二叉树前序遍历算法如下(第二种方法实现前序遍历)：

（1）初始化设置一个堆栈；
（2）把根结点指针入栈；
（3）当堆栈非空时，循环执行步骤（3.a）到步骤（3.c）；
（3.a）出栈取得一个结点指针，访问该结点；
（3.b）若该结点的右子树非空，则将该结点的右子树指针入栈；
（3.c）若该结点的左子树非空，则将该结点的左子树指针入栈；
（4）结束。

一个简单练习：
一棵完全二叉树有5000个结点，可以计算出其叶结点的个数是（）个？

n0=n2+1 => n2=n0-1
5000 = n0+n1+n2 = 2n0-1+n1
由于是完全二叉树
因此n1 = 0(无解） 或 n1 = 1（此时n0=2500）
所以结果是2500

---

0x03 线索二叉树

---

二叉树的遍历有两种情况，一种是一次性遍历；另一种是分步遍历。分步遍历是指在规定了一棵二叉树的遍历方法后，每次只访问当前结点的数据域值，然后使结点为当前结点的后继结点，直到到达二叉树的最后一个结点为止。分步遍历方法提供了对二叉树进行循环遍历操作的工具。

线索二叉树既可以从前向后分步遍历二叉树，也可以从后向前分步遍历二叉树。

当按某种规则遍历二叉树时，保存遍历时得到的结点的后继结点信息和前驱结点信息的最常用的方法是建立线索二叉树。

对二叉链存储结构的二叉树分析可知，在有n个结点的二叉树中必定存在n+1个空链域。

线索二叉树有如下规定：当某结点的左指针为空时，令该指针指向按某种方法遍历二叉树时得到的该结点的前驱结点；当某结点的右指针为空时，令该指针指向按某种方法遍历二叉树时得到的该结点的后继结点。仅仅这样做会使我们不能区分左指针指向的结点到底是左孩子结点还是前驱结点，右指针指向的结点到底是右孩子结点还是后继结点。因此我们再在结点中增加两个线索标志位来区分这两种情况。线索标志位定义如下：

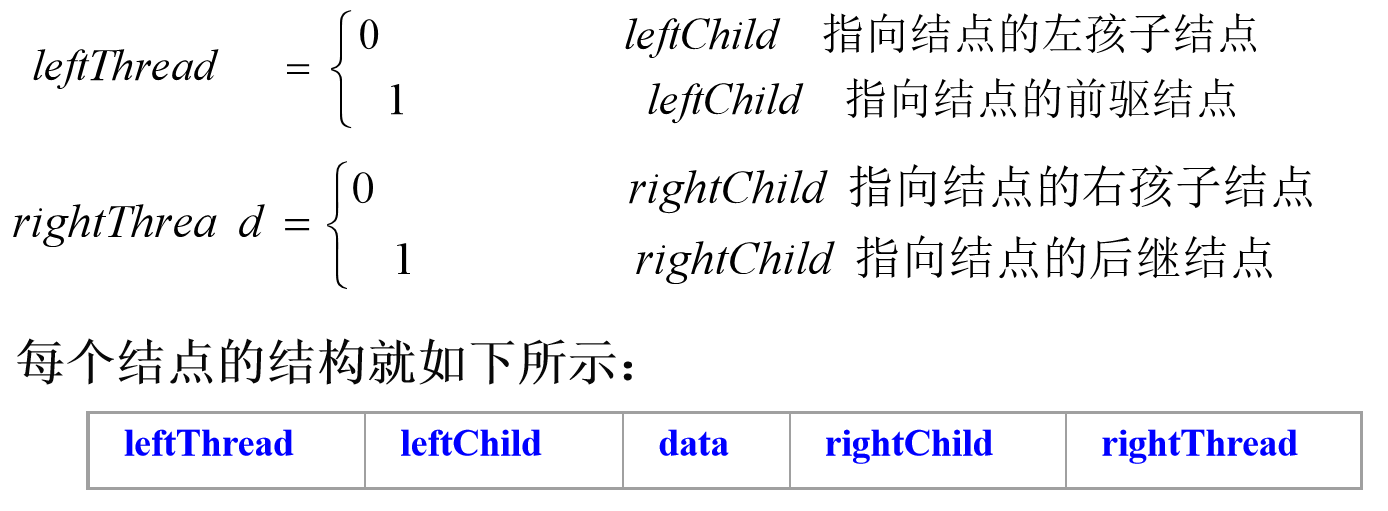
结点中指向前驱结点和后继结点的指针称为线索（本质还是指针）。在二叉树的结点上加上线索的二叉树称作线索二叉树。对二叉树以某种方法（如前序、中序或后序方法）遍历使其变为线索二叉树的过程称作按该方法对二叉树进行的线索化。

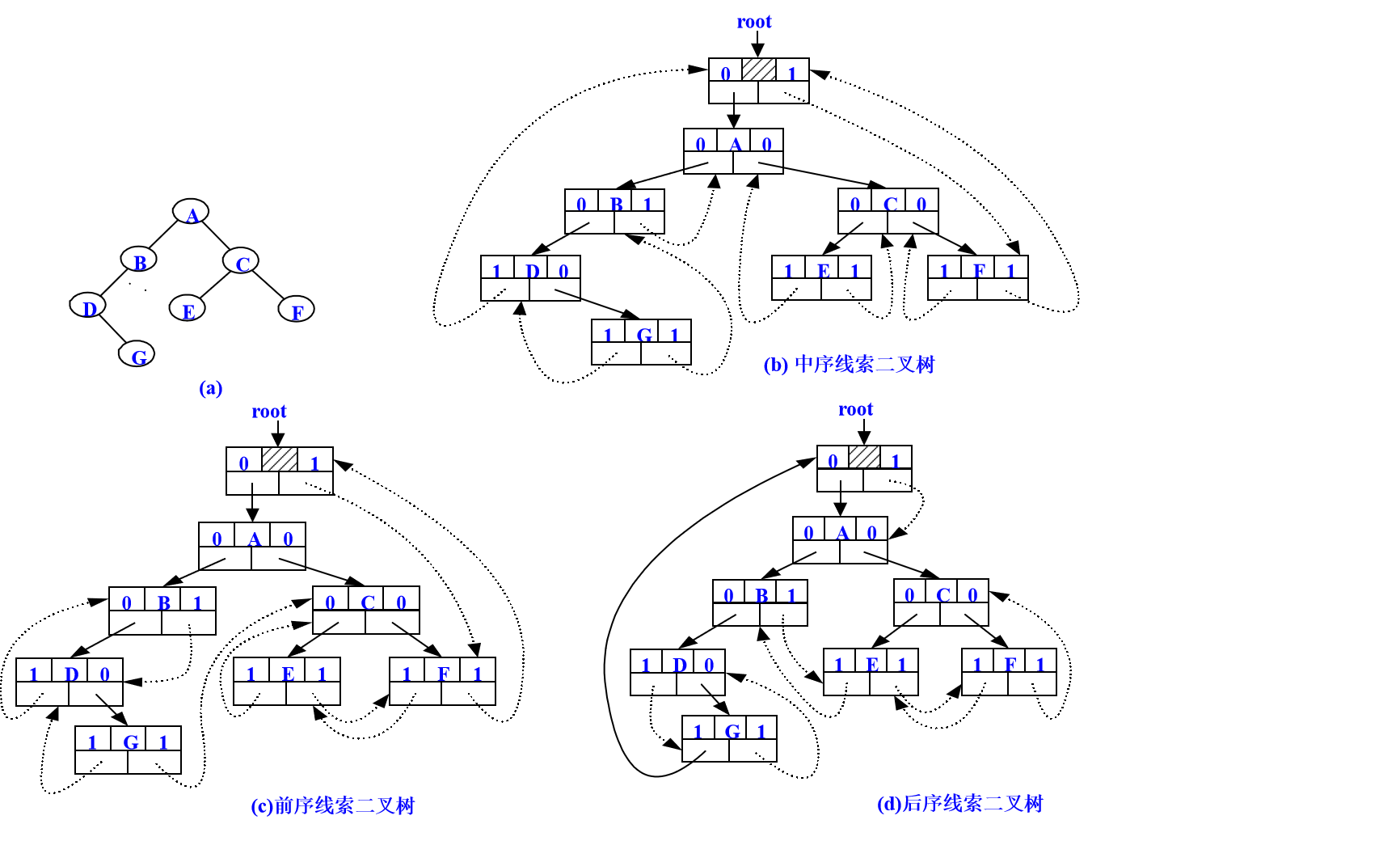
如上图，
前序遍历：ABDGCEF B的后继是D
中序遍历：DGBAECF B的后继是A
后序遍历：GDBEFCA B的后继是E
从图中可以看出B的后继指向的结点是不同的。

---

0x04 哈夫曼树

---

哈夫曼树

从A结点到B结点所经过的分支序列叫做从A结点到B结点的路径；
从A结点到B结点所经过的分支个数叫做从A结点到B结点的路径长度；
从二叉树的根结点到二叉树中所有叶结点的路径长度之和称作该二叉树的路径长度。

设二叉树有n个带权值的叶结点，定义从二叉树的根结点到二叉树中所有叶结点的路径长度与相应叶结点权值的乘积之和称作该二叉树的带权路径长度（WPL）

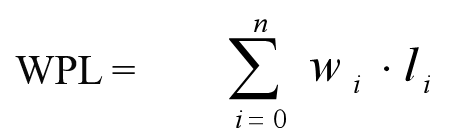
其中，wi为第i个叶结点的权值，li为从根结点到第i个叶结点的路径长度。

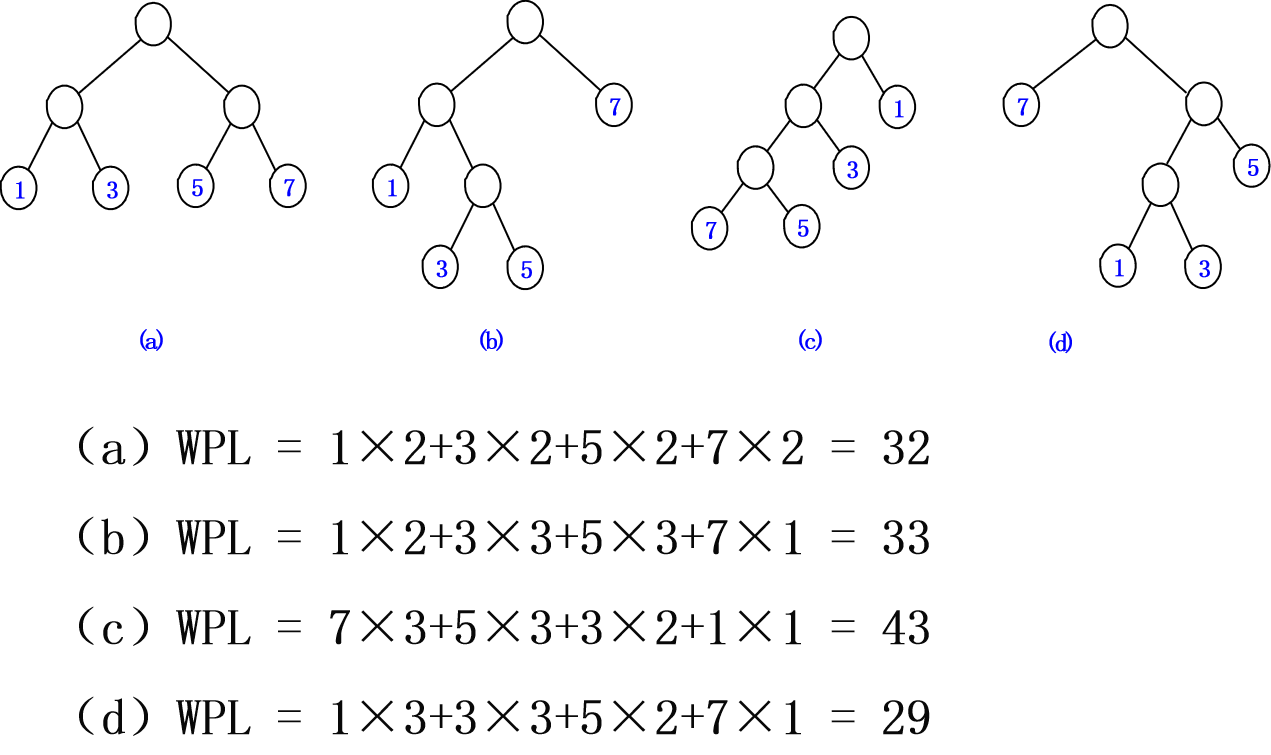
具有最小带权路径长度的二叉树称作哈夫曼（Huffman）树（或称最优二叉树）。要使一棵二叉树的带权路径长度WPL值最小，必须使权值越大的叶结点越靠近根结点。哈夫曼树构造算法为：

（1）由给定的n个权值{w1,w2,…,wn}构造n棵只有根结点的二叉树，从而得到一个二叉树森林F={T1,T2,…,Tn}。
（2）在二叉树森林F中选取根结点的权值最小和次小的两棵二叉树作为新的二叉树的左右子树构造新的二叉树，新的二叉树的根结点权值为左右子树根结点权值之和。
（3）在二叉树森林F中删除作为新二叉树左右子树的两棵二叉树，将新二叉树加入到二叉树森林F中。
（4）重复步骤（2）和（3），当二叉树森林F中只剩下一棵二叉树时，这棵二叉树就是所构造的哈夫曼树。

可参看下列链接：
https://baijiahao.baidu.com/s?id=1663514710675419737&wfr=spider&for=pc

哈夫曼树应用

哈夫曼编码问题

将传送的文字转换为二进制字符0和1组成的二进制串的过程为编码。
哈夫曼树可用于构造代码总长度最短的编码方案。
具体构造方法如下：

设需要编码的字符集合为{d1,d2,…,dn}，
各个字符在电文中出现的次数集合为{w1,w2,…,wn}，
以d1,d2,…,dn作为叶结点，
以w1,w2,…,wn作为各叶结点的权值
构造一棵二叉树，
规定哈夫曼树中的左分支为0，
右分支为1，
则从根结点到每个叶结点所经过的分支
对应的0和1组成的序列
便为该结点对应字符的编码。
代码总长度最短的不等长编码
称之为哈夫曼编码。

---

0x05 数与二叉树的转换

---

树转换为二叉树

（1）树中所有相同双亲结点的兄弟结点之间加一条连线。
（2）对树中不是双亲结点第一个孩子的结点，只保留新添加的该结点与左兄弟结点之间的连线，删去该结点与双亲结点之间的连线。
（3）整理所有保留的和添加的连线，使每个结点的第一个孩子结点连线位于左孩子指针位置，使每个结点的右兄弟结点连线位于右孩子指针位置。

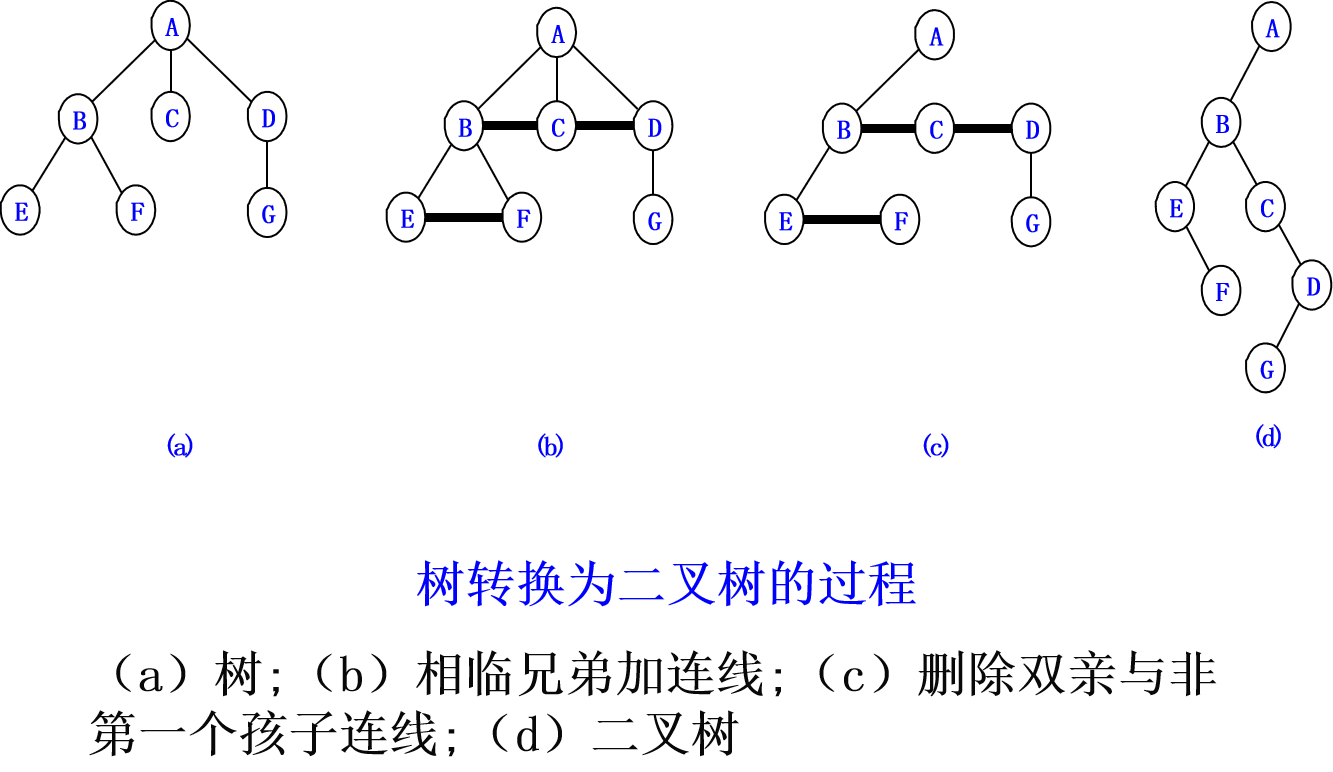
二叉树还原为树

（1）若某结点是其双亲结点的左孩子，则把该结点的右孩子、右孩子的右孩子……都与该结点的双亲结点用线连起来。
（2）删除原二叉树中所有双亲结点与右孩子结点的连线。
（3）整理所有保留的和添加的连线，使每个结点的所有孩子结点位于相同层次高度。

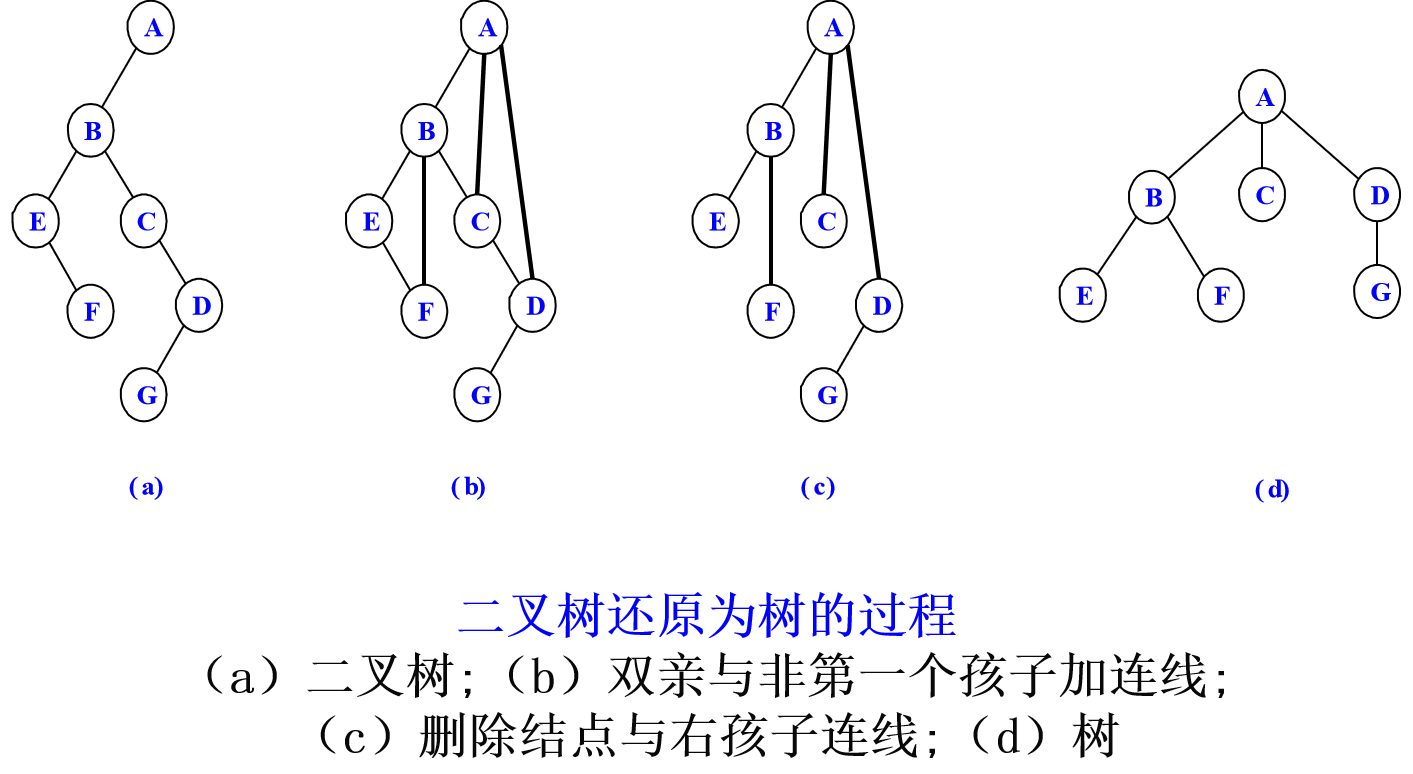
0x06 树的遍历

树的遍历算法主要有先根遍历算法和后根遍历算法两种。

树的先根遍历递归算法为：

（1）访问根结点；
（2）按照从左到右的次序先根遍历根结点的每一棵子树。

注意：树的先根遍历序列一定和该树转换的二叉树的先序遍历序列相同。

树的后根遍历递归算法为：

（1）按照从左到右的次序后根遍历根结点的每一棵子树；
（2）访问根结点。

注意：树的后根遍历序列一定和该树转换的二叉树的中序遍历序列相同。