Cuda C++：Tensor Core 数值行为分析之测试复现

参考

B. Hickmann and D. Bradford, "Experimental Analysis of Matrix Multiplication Functional Units," 2019 IEEE 26th Symposium on Computer Arithmetic (ARITH), Kyoto, Japan, 2019, pp. 116-119, doi: 10.1109/ARITH.2019.00031.
Massimiliano Fasi, Nicholas J. Higham, Mantas Mikaitis, and Srikara Pranesh "Numerical behavior of NVIDIA tensor cores" and Presentation

设备

手上只有消费级显卡，用的是 Ada Lovelace 架构的 RTX4060（sm_89）。

测试模板

本质上是基于 2. 的实验复现，写了一个 Cuda C++ 的比较灵活的测试框架，能够适应各种不同的浮点类型（FP16/FP32/BF16/TF32）。

common.cuh

#pragma once

#include <cstdio>
#include <cstdlib>
#include <mma.h>
#include <cuda_fp16.h>

using namespace nvcuda;

template<typename AType, typename BType, typename CType, typename DType, int M, int N, int K>
__global__ void tensorcore_test_kernel(
    const AType* a_mat,
    const BType* b_mat, 
    CType c_val,
    DType* d_mat
) {
    wmma::fragment<wmma::matrix_a, M, N, K, AType, wmma::row_major> a_frag;
    wmma::fragment<wmma::matrix_b, M, N, K, BType, wmma::col_major> b_frag;
    wmma::fragment<wmma::accumulator, M, N, K, CType> c_frag;
    wmma::fragment<wmma::accumulator, M, N, K, DType> d_frag;
    
    wmma::load_matrix_sync(a_frag, a_mat, K);
    wmma::load_matrix_sync(b_frag, b_mat, K);
    wmma::fill_fragment(c_frag, (CType)c_val);
    
    wmma::mma_sync(d_frag, a_frag, b_frag, c_frag);
    
    wmma::store_matrix_sync(d_mat, d_frag, N, wmma::mem_row_major);
}

template<typename FType>
void print_binary(FType value) {
	if constexpr (sizeof(FType) == 4) {
		unsigned int bits = *((unsigned int*)&value);
		printf("%d ", (bits >> 31) & 1);
		for(int i = 30; i >= 23; i--) printf("%d", (bits >> i) & 1);
		printf(" ");
		for(int i = 22; i >= 0; i--) printf("%d", (bits >> i) & 1);
		printf("\n");
	} else if constexpr (sizeof(FType) == 2) {
		unsigned short bits = *((unsigned short*)&value);
		printf("%d ", (bits >> 15) & 1);
		for(int i = 14; i >= 10; i--) printf("%d", (bits >> i) & 1);
		printf(" ");
		for(int i = 9; i >= 0; i--) printf("%d", (bits >> i) & 1);
		printf("\n");
	}
}

void print_binary_tf32(float value) {
	unsigned int bits = *((unsigned int*)&value);
	printf("%d ", (bits >> 31) & 1);
	for(int i = 30; i >= 23; i--) printf("%d", (bits >> i) & 1);
	printf(" ");
	for(int i = 22; i >= 13; i--) printf("%d", (bits >> i) & 1);
	printf("\n");
}

template<typename AType, typename BType, typename CType, typename DType>
DType run_test(const AType* a_vals, const BType* b_vals, CType c_val, const char* test_name) {
    const int M = 16, N = 16, K = 16;
    
    AType *deviceA, *hostA;
    BType *deviceB, *hostB;
    DType *deviceD, *hostD;
    
    hostA = (AType*)malloc(M * K * sizeof(AType));
    hostB = (BType*)malloc(K * N * sizeof(BType));
    hostD = (DType*)malloc(M * N * sizeof(DType));
    
    cudaMalloc(&deviceA, M * K * sizeof(AType));
    cudaMalloc(&deviceB, K * N * sizeof(BType));
    cudaMalloc(&deviceD, M * N * sizeof(DType));
    
    for(int i = 0; i < M * K; i++) hostA[i] = (AType)0;
    for(int i = 0; i < K * N; i++) hostB[i] = (BType)0;
    
    for(int i = 0; i < 4; i++) {
        hostA[i] = a_vals[i];
    }
    
    for(int i = 0; i < 4; i++) {
        hostB[i] = b_vals[i];
    }
    
    cudaMemcpy(deviceA, hostA, M * K * sizeof(AType), cudaMemcpyHostToDevice);
    cudaMemcpy(deviceB, hostB, K * N * sizeof(BType), cudaMemcpyHostToDevice);
    
    tensorcore_test_kernel
		<AType, BType, CType, DType, 16, 16, 16>
		<<<1, 32>>>(deviceA, deviceB, c_val, deviceD);
    
    cudaMemcpy(hostD, deviceD, M * N * sizeof(DType), cudaMemcpyDeviceToHost);
    
    DType result = hostD[0];
    
    free(hostA);
    free(hostB);
    free(hostD);
    
    cudaFree(deviceA);
    cudaFree(deviceB);
    cudaFree(deviceD);
    
	printf("> Test: %s\n", test_name);
	printf("  Result: ");
	if constexpr (sizeof(DType) == 2) {
		printf("%e | ", (float)__half2float(result));
	} else {
		printf("%e | ", result);
	}
	print_binary(result);
    return result;
}

inline float bits_to_float(unsigned int bits) {
    return *((float*)&bits);
}

下面尝试以 FP16 * FP16 + FP32 -> FP32 为例构建测试集：

测试用例

一组测试用例代表一次点积和一次加法：

\[d_{11} = a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} + a_{14}b_{41} + c_{11} \]

包含四次乘法和一次 5 元累加器（5-operand adder）。

程序中调用一次 run_test<half, half, float, float>(a_vals, b_vals, c_val, "..."); 来实现一次测试，输出结果及其二进制表示。

次正规数支持

FP16 Subnormal

{
    half a_vals[4] = {__float2half(ldexp(1., -24)), 0, 0, 0};
    half b_vals[4] = {__float2half(4.0), 0, 0, 0};
    float c_val = 0;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Subnormal numbers, test #1");
} // 2^-22 if FP16 subnormal is supported

输出：

> Test: Subnormal numbers, test #1
  Result: 2.384186e-07 | 0 01101001 00000000000000000000000

结果 \(2^{-22}\) 正确，Tensor Core 支持 FP16 的次正规数。

FP32 Subnormal

{
    half a_vals[4] = {0, 0, 0, 0};
    half b_vals[4] = {0, 0, 0, 0};
    float c_val = ldexp(1., -149);
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Subnormal numbers, test #2");
} // 2^-149 if FP32 subnormal is supported

输出：

> Test: Subnormal numbers, test #2
  Result: 1.401298e-45 | 0 00000000 00000000000000000000001

结果 \(2^{-149}\) 正确，Tensor Core 支持 FP32 的次正规数。

Subnormal 产生测试

{
    half a_vals[4] = {__float2half(ldexp(1., -14)), 0, 0, 0};
    half b_vals[4] = {__float2half(ldexp(1., -1)), 0, 0, 0};
    half c_val = 0;
    run_test<half, half, half, half>(a_vals, b_vals, c_val, "Subnormal numbers, test #3/1");
    b_vals[0] = __float2half(1.0);
    c_val = __float2half(ldexp(-1., -15));
    run_test<half, half, half, half>(a_vals, b_vals, c_val, "Subnormal numbers, test #3/2");
} // 2^-15 (for both) if subnormal can be produced

输出：

> Test: Subnormal numbers, test #3/1
  Result: 3.051758e-05 | 0 00000 1000000000
> Test: Subnormal numbers, test #3/2
  Result: 3.051758e-05 | 0 00000 1000000000

结果都是 \(2^{-15}\)，证明 Tensor Core 能够产生次正规数。

点积准确性测试

精度测试

{
    half a_vals[4] = {
        __float2half(1. - ldexp(1, -11)), __float2half(1. - ldexp(1, -11)),
        __float2half(1. - ldexp(1, -11)), __float2half(1. - ldexp(1, -11))};
    half b_vals[4] = {
        __float2half(1. - ldexp(1, -11)), __float2half(1. - ldexp(1, -11)),
        __float2half(1. - ldexp(1, -11)), __float2half(1. - ldexp(1, -11))};
    float c_val = 0;
    float expected_d_val = 4 * (1 - ldexp(1, -10) + ldexp(1, -22));
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Exact product of binary16 inputs");
    printf("  expected: ");
    print_binary(expected_d_val);
} // 4*(1 - 2^-10 + 2^-22) if no precision loss

输出：

> Test: Exact product of binary16 inputs
  Result: 3.996095e+00 | 0 10000000 11111111100000000000100
  expected: 0 10000000 11111111100000000000100

结果和预期的 \(4(1-2^{-10}+2^{-22})\) 相符。

FP16 模式下中间精度测试

{
    half a_vals[4] = {
        __float2half(1. - ldexp(1, -11)), __float2half(1. - ldexp(1, -11)), 0, 0};
    half b_vals[4] = {
        __float2half(1. - ldexp(1, -11)), __float2half(ldexp(1, -11)), 0, 0};
    half c_val = __float2half(0.);
    run_test<half, half, half, half>(a_vals, b_vals, c_val, "Temporary overflow in the Tensor Cores (all fp16)");
} // 1 - 2^-10 + 2^-11 if temporary (fp16) overflow is supported

输出：

> Test: Temporary overflow in the Tensor Cores (all fp16)
  Result: 9.995117e-01 | 0 01110 1111111111

结果 \(1-2^{-10}+2^{-11}\)，说明即使输出为 FP16，硬件计算也是以 FP32 进行的，舍入到 FP16 是软件层面的。

舍入误差与加法顺序

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(ldexp(1, -25)), __float2half(ldexp(1, -25)),
        __float2half(ldexp(1, -25)), __float2half(ldexp(1, -25))};
    float c_val = 1;
    run_test<half, half, float, float>(a_vals, b_vals, c_val,
                                       "Accuracy of the 5-operand adder in the Tensor Cores (c=1)");
    c_val = ldexp(1, -25);
    for (int i = 0; i < 4; i++) {
        char test_name[100];
        sprintf(test_name, "Accuracy of the 5-operand adder in the Tensor Cores (b[%d]=1), test %d", i + 1, i + 1);
        b_vals[i] = __float2half(1.);
        run_test<half, half, float, float>(a_vals, b_vals, c_val, test_name);
        b_vals[i] = __float2half(ldexp(1, -25));
    }
} // 1 for all permutations if rounded before adding
  // 2^(-25) not 2^(-24) because of the one extra bit in the significand alignment

输出：

> Test: Accuracy of the 5-operand adder in the Tensor Cores (c=1)
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000
> Test: Accuracy of the 5-operand adder in the Tensor Cores (b[1]=1), test 1
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000
> Test: Accuracy of the 5-operand adder in the Tensor Cores (b[2]=1), test 2
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000
> Test: Accuracy of the 5-operand adder in the Tensor Cores (b[3]=1), test 3
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000
> Test: Accuracy of the 5-operand adder in the Tensor Cores (b[4]=1), test 4
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000

均输出 1，说明对于所有可能的累加顺序而言，会先对数值进行舍入，在最坏情况下会有四次舍入误差；加法器的顺序会从较大的值开始——这在执行指数对齐时是必要的。

由于存在保护位（见下方“加法器特性测试”），应当使用 \(2^{-25}\) 而不是 \(2^{-24}\) 测试。

舍入模式

IEEE 754 规定了四种舍入模式：RN（就近舍入），RZ（向零舍入），RU（向正无穷舍入）和 RD（向负无穷舍入）：

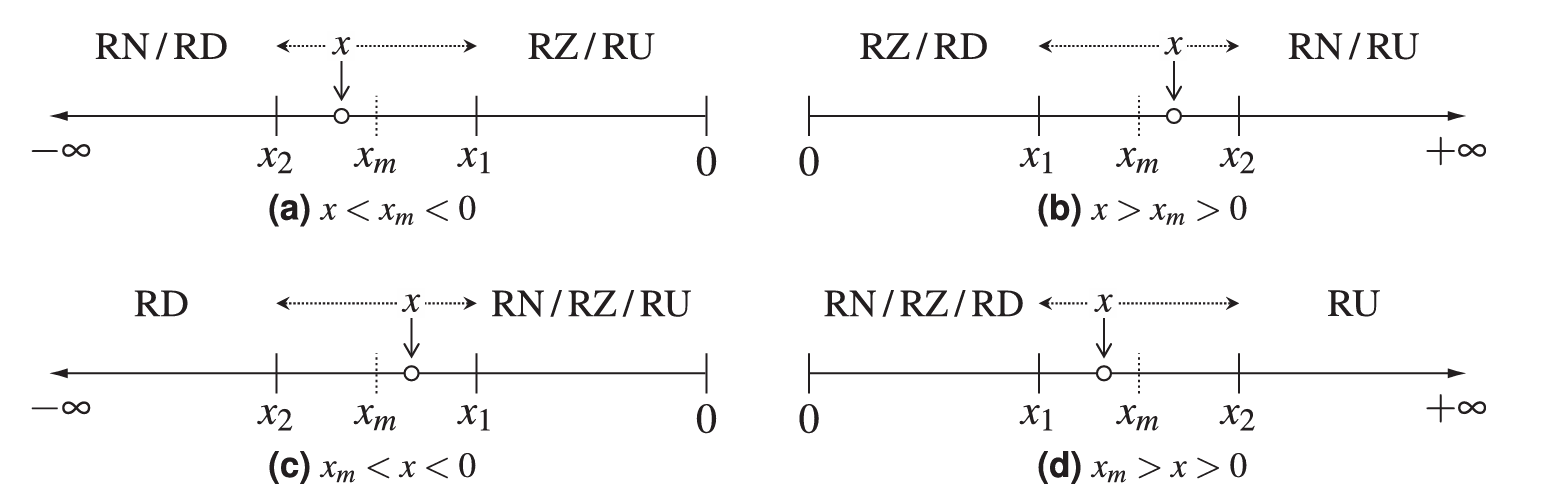
加法器舍入模式

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(2.), __float2half(ldexp(1, -23) + ldexp(1, -24)),
        __float2half(0), __float2half(0)};
    float c_val = 0;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Rounding-mode for adder test 1");
} // 2 if rounding mode is RZ or RD

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(-2.), __float2half(-ldexp(1, -23) - ldexp(1, -24)),
        __float2half(0), __float2half(0)};
    float c_val = 0;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Rounding-mode for adder test 2");
} // -2 if rounding mode is RZ

使用两组对称的测试，估计加法器在正负数上的舍入模式。输出：

> Test: Rounding-mode for adder test 1
  Result: 2.000000e+00 | 0 10000000 00000000000000000000000
> Test: Rounding-mode for adder test 2
  Result: -2.000000e+00 | 1 10000000 00000000000000000000000

第一次尝试得到 \(2\)，说明可能是 RZ 或 RD；第二次得到 \(-2\)，说明是 RZ。

FP32 到 FP16 舍入模式测试

{
    half a_vals[4] = {
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24)), 0, 0};
    half b_vals[4] = {
        __float2half(ldexp(1, -1)), __float2half(ldexp(1, -2)), 0, 0};
    half c_val = __float2half(0.);
    run_test<half, half, half, half>(a_vals, b_vals, c_val, "Rounding-mode test for FP32 to FP16 conversion");
} // 0 if RZ is used, and 2^-24 if RZ is not used
// which means FP32 to FP16 conversion is done by software.

输出：

> Test: Rounding-mode test for FP32 to FP16 conversion
  Result: 5.960464e-08 | 0 00000 0000000001

结果为 \(2^{-24}\)，表明 RZ 并没有被采用，作为软件层面的操作，这里的舍入策略和加法器不同。

加法器特性研究

对齐保护位

{
    half a_vals[4] = {__float2half(1.), 0, 0, 0};
    half b_vals[4] = {__float2half(1.), 0, 0, 0};
    float c_val = ldexp(1, -24) - 1.0;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Extra bits in the significand alignment");
} // 2^-24 if extra bits in the significand alignment are supported

输出：

> Test: Extra bits in the significand alignment
  Result: 5.960464e-08 | 0 01100111 00000000000000000000000

得到结果 \(2^{-24}\)，说明存在至少一位保护位，以改善截断导致的精度误差。

这点和论文用的 V100 卡测试结果不同，但原文提到 T4 和 A100 也是存在保护位的，因此并不意外。

加法归一化时机

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24)),
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24))};
    float c_val = 1.0 - ldexp(1, -24);
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Normalization in addition");
} // 1 + 2^-23 if halfway-normalization in addition is not supported

如果 5 元加法器不支持对部分和归一化，可能导致精度的丢失。输出：

> Test: Normalization in addition
  Result: 1.000000e+00 | 0 01111111 00000000000000000000001

结果似乎为 \(1\)，但观察二进制发现其实是 \(1+2^{-23}\)，而如果保持归一化，\(1+2^{-24}\) 时会因为指数差异过大而无法表示，最后保持为 \(1\) 直至输出。因此加法归一化仅在输出时使用。

减法归一化时机

和上面同理，但是出现了和论文不同的结果：

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(1.), -__float2half(ldexp(1, -24)), 0, 0};
    float c_val = ldexp(1, -24) - 1.0;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Normalization in subtraction");
} // 0 if halfway-normalization in subtraction is supported(?)
  // not sure because of extra guard bits.

输出：

> Test: Normalization in subtraction
  Result: 0.000000e+00 | 0 00000000 00000000000000000000000

考虑到保护位的存在，结果得到 0（表示存在部分和正规化？）可能是保护位暂存的部分精度导致，因此这个测试集无法直接说明结论。

额外溢出位

由于没有部分和正规化，运算途中可能出现因为进位而整数位溢出的情况。

{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(ldexp(1, -23))};
    float c_val = 1.0 + ldexp(1, -22) + ldexp(1, -23);
    for (int i = 1; i <= 4; i++) {
        char test_name[100];
        sprintf(test_name, "Extra bits for carry out : 2 bits, test %d", i);
        run_test<half, half, float, float>(a_vals, b_vals, c_val, test_name);
        std::swap(b_vals[(i + 2) % 4], b_vals[i - 1]);
    }
} // 4 + 2^-21 for all if 2 extra bits for carry out are supported
{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(1.), __float2half(1.5),
        __float2half(1.75), __float2half(1.875)};
    float c_val = 1.875;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Extra bits for carry out : 3 bits");
} // 8 if 3 extra bits for carry out are supported

采用排列是因为消除加法顺序（对于相同值之间）可能的影响。输出：

> Test: Extra bits for carry out : 2 bits, test 1
  Result: 4.000000e+00 | 0 10000001 00000000000000000000001
> Test: Extra bits for carry out : 2 bits, test 2
  Result: 4.000000e+00 | 0 10000001 00000000000000000000001
> Test: Extra bits for carry out : 2 bits, test 3
  Result: 4.000000e+00 | 0 10000001 00000000000000000000001
> Test: Extra bits for carry out : 2 bits, test 4
  Result: 4.000000e+00 | 0 10000001 00000000000000000000001
> Test: Extra bits for carry out : 3 bits
  Result: 8.000000e+00 | 0 10000010 00000000000000000000000

都输出了正确的结果，可以推断至少有三个额外溢出位。

单调性测试

当运算结果满足 \(\forall x_i \le y_i \to \sum_i x_i \le \sum_i y_i\) 时，就说明满足单调性（monotonicity）。由于精度问题，这个显然的性质在浮点计算下并不容易保证。

printf("MONOTONICITY OF THE DOT PRODUCTS TESTS\n");
{
    half a_vals[4] = {
        __float2half(1.), __float2half(1.),
        __float2half(1.), __float2half(1.)};
    half b_vals[4] = {
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24)),
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24))};
    float c_val = 1 - ldexp(1, -24);
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Monotonicity of the dot products test 1 (less in exact)");
    c_val = 1;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Monotonicity of the dot products test 2 (larger in exact)");
} // ... not good testcase because of extra guard bits.

{
    half a_vals[4] = {
        __float2half(0.5), __float2half(0.5),
        __float2half(0.5), __float2half(0.5)};
    half b_vals[4] = {
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -24)),
        __float2half(ldexp(1, -24)), __float2half(ldexp(1, -23) + ldexp(1, -24))};
    float c_val = 1 - ldexp(1, -24);
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Monotonicity of the dot products test 1+ (less in exact)");
    c_val = 1;
    run_test<half, half, float, float>(a_vals, b_vals, c_val, "Monotonicity of the dot products test 2+ (larger in exact)");
} // improved testcase.

仍然是由于保护位，对于 V100 的测试数据，需要再进一步完善：

MONOTONICITY OF THE DOT PRODUCTS TESTS
> Test: Monotonicity of the dot products test 1 (less in exact)
  Result: 1.000000e+00 | 0 01111111 00000000000000000000001
> Test: Monotonicity of the dot products test 2 (larger in exact)
  Result: 1.000000e+00 | 0 01111111 00000000000000000000010
> Test: Monotonicity of the dot products test 1+ (less in exact)
  Result: 1.000000e+00 | 0 01111111 00000000000000000000001
> Test: Monotonicity of the dot products test 2+ (larger in exact)
  Result: 1.000000e+00 | 0 01111111 00000000000000000000000

第一次测试没有看出问题，但第二组表明单调性其实是没有满足的。

小结

数值行为的推断实验是为了弥补 Tensor Core 运算机制的半透明的遗憾，如果能精准模拟数值行为，就能复现运算精度并不高的机器学习等实验，从而设计完善的数值误差分析工具，精准模拟硬件行为，乃至优化实验的可再现性。

同时，不难发现，随着 Tensor Core 的不断迭代——论文采用的 V100 是第一代，A100 是第三代，而 RTX4060 已经是第四代——其精度水平也在不断提升，因此对于这些持续升级的硬件机构，持续做这些分析是有必要的。

posted @ 2025-11-10 18:53 Lice_wx 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部