【整活】示波器动画初体验
前言
前段时间打电赛的时候,偶然发现一个叫 Oscilloscope Music 的东西,之前从来没想过示波器能这么玩,可谓是大开眼界了。
现在闲下来便想自己试一试,可惜不懂乐理,就试试单纯显示动画吧。
示波器模拟器效果:
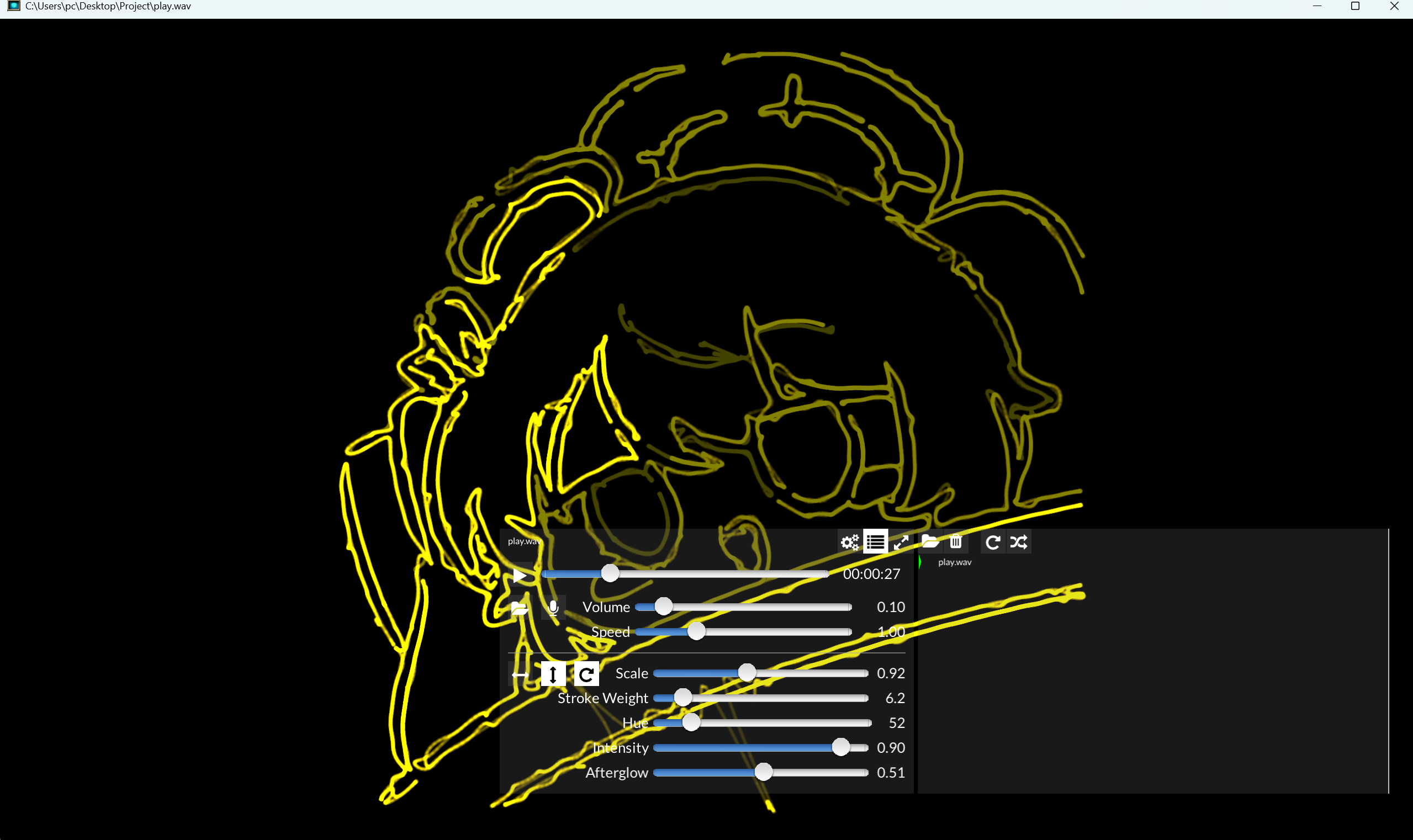
原理
默认状态下,示波器使用的是 Y-T 模式,也就是横坐标是时间,纵坐标是电压,是最常规的示波器模式。
当双踪示波器使用 X-Y 模式时,横坐标和纵坐标分别为两个通道的电压值。这个模式通常用于显示李萨如图形,用来判断信号的相位等信息。这次要绘制的自定义图像其实就是某种比较复杂的李萨如图形,但现在已经和李萨如图形本身的各种理论已经关系不大了。
也就是说,本质上就是要操纵示波器电子打到荧光屏幕的位置,并快速移动,通过余晖使得屏幕显示一个稳定的图线。
思路
- 首先,我们得到一张原始图片(画师 @zzul);
- 然后要把它变成我们比较容易处理的形式,比如 bmp 格式;
- 然后示波器是没有多种颜色的,于是转化为灰度图像;
// RGB to grayscale conversion using standard luminance formula uint8_t rgbToGrayscale(const PixelRGB& pixel) { return static_cast<uint8_t>(0.299 * pixel.r + 0.587 * pixel.g + 0.114 * pixel.b); } - 然后由于不少示波器都没有 Z 轴的调节选项,灰度大小其实也是没有意义的。合理的办法其实是绘制出图像的轮廓,于是采用边缘检测算法提取出轮廓部分,这时候图像也就变成二值图像了;
- 然后设计一个合理的绘制路径;
- 最后整合成 wav 文件,用耳机线转 BNC 接到示波器上。

细节
这个东西嘛,口胡起来是很容易的,但是真写起来就很讨厌了。
麻烦的点主要是东西太多了,不过很多像解析 BMP,生成 WAV 文件,Canny 边缘检测算法这种纯码农的活,不妨丢给 AI 去干。
对我而言,想的挺久的其实是如何对着 Canny 算法的结果取生成一个合适的绘制路径。
实际的电信号不会发生数学意义上的真正突变。比如像方波这种信号,如果用示波器观察,时基调的很小,会发现突变的斜率也不是无穷大。
所有不能直接把 Canny 边缘检测得到的所有边缘点都拿过来,随便搞一个顺序打到示波器上,不然会有大量影响观感的飞线。
现在问题就是,对一个黑白矩阵,取一条覆盖所有白点的线,要求经过黑色部分的欧几里得距离之和尽量小(飞线尽量少),白点覆盖次数尽可能接近(亮度尽量均匀)。
哎,怎么变成图论题了,一个示波器闹麻了。但是有一说一这个挺有意思的,就想了下怎么做。
首先考虑覆盖白点。很容易想到 TSP 问题,但是解决这个问题代价太高,需要退而求其次选一些近似算法或者贪心算法平替。这方面我不是很熟,就没仔细想。
最小生成树(MST)方案
我的思路是优先考虑如何链接所有白色的区域,这个和最小生成树的思想很接近。倒不是说 MST 是最好的,而是它思路成熟简单,这样不会遇到太多理论的难题,而且效果足够好。
比如两个白色连通块 \(S_1 = \{\cdots\}, S_2 = \{\cdots\}\),那么链接二者的飞线代价就是 \(\min_{P\in S_1, Q\in S_2} \{\text{dist}(P, Q)\}\)。
把每个白色连通块抽象成点,边的长度就是上面的最小距离,得到一张完全图。应用 Prim 算法构建最小生成树。
在 DFS 搜索连通块时保留括号序,构建 MST 时记录飞线链接的具体点位,可以方便绘制路径的构建。
vector<pii> points;
vector<vector<pii>> edges; // bracket order of dfs
matrix<bool> visited;
matrix<int> belong;
matrix<int> dfn;
const int dx[] = {-1, -1, -1, 0, 0, 1, 1, 1};
const int dy[] = {-1, 0, 1, -1, 1, -1, 0, 1};
void dfs(int x, int y, int e) {
points.push_back(std::make_pair(x, y));
dfn[x][y] = points.size() - 1;
visited[x][y] = true;
edges[e].push_back(std::make_pair(x, y));
belong[x][y] = e;
int height = grayMatrix.size();
int width = grayMatrix[0].size();
for (int d = 0; d < 8; d++) {
int nx = x + dx[d];
int ny = y + dy[d];
if (nx >= 0 && nx < height && ny >= 0 && ny < width && grayMatrix[nx][ny] == 255 && !visited[nx][ny]) {
dfs(nx, ny, e);
}
}
edges[e].push_back(std::make_pair(x, y));
}
void construct_signal() {
int height = grayMatrix.size();
int width = grayMatrix[0].size();
visited = matrix<bool>(height, vector<bool>(width, false));
belong = matrix<int>(height, vector<int>(width, -1));
dfn = matrix<int>(height, vector<int>(width, -1));
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
if (grayMatrix[i][j] == 255) {
if (visited[i][j]) {
continue;
}
edges.push_back(vector<pii>());
dfs(i, j, edges.size() - 1);
}
}
}
std::cout << "points : " << points.size() << std::endl;
dist = matrix<distance>(edges.size(), vector<distance>(edges.size()));
for (int i = 0; i < points.size(); i++) {
for (int j = i + 1; j < points.size(); j++) {
distance d(points[i], points[j]);
int u = belong[points[i].first][points[i].second];
int v = belong[points[j].first][points[j].second];
if (d < dist[u][v]) {
dist[u][v] = d;
std::swap(d.p1, d.p2);
dist[v][u] = d;
}
}
}
prim_MST();
travel(root, -1, edges[root][0]);
std::cout << "edges : " << edges.size() << std::endl;
std::cout << "signal length: " << signalXY.size() << std::endl;
}
记白点总数为 \(N\),连通块个数为 \(M\),这个部分的时间复杂度为 \(O(N^2)\),是整个算法的时间瓶颈。
可能存在更高效的实现,不过我没有找到比较好写的。但目前来看,限于示波器分辨率、声卡播放频率等因素,大图片的效率提升其实意义不大。
构造路径
比较麻烦的是对着 MST 的树形结构,把路径跑出来(travel 函数)。
void travel(int u, int fa, pii starting_point) {
for (auto it = mst[u].begin(); it != mst[u].end(); it++) {
if (it->to_edge() == fa) {
mst[u].erase(it);
break;
}
}
std::sort(mst[u].begin(), mst[u].end(), [&](const distance& a, const distance& b) {
pii pa = a.p1, pb = b.p1;
return dfn[pa.first][pa.second] < dfn[pb.first][pb.second];
});
auto cur_edge_it = edges[u].begin();
auto go_to_next = [&]() {
++cur_edge_it;
if (cur_edge_it == edges[u].end()) {
cur_edge_it = edges[u].begin();
// ++cnt;
}
};
while (*cur_edge_it != starting_point) {
go_to_next();
}
auto starting_it = cur_edge_it;
for (auto v : mst[u]) {
while (*cur_edge_it != v.p1) {
signalXY.push_back(*cur_edge_it);
go_to_next();
}
signalXY.push_back(*cur_edge_it);
travel(v.to_edge(), u, v.p2);
}
do {
signalXY.push_back(*cur_edge_it);
go_to_next();
} while (cur_edge_it != starting_it);
}
这个本质也就是个比较史的 DFS。首先进去我们把 MST 的父边删掉,再将孩子边按照飞出点在连通块内的 DFS 序(也就是括号序的左括号)排序。
为什么要排序呢?当我们从孩子边 \(u\to v_1\) 转到 \(u\to v_2\) 的时候,从连通块飞线出去的位置是不一样的,如果直接直线走可能会造成更多不必要的飞线:
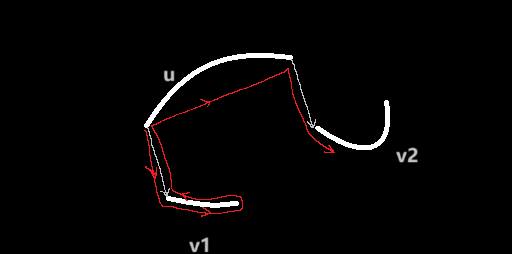
上面的 case,我们希望中间过渡的部分能从 \(u\) 内部过,这样就没有这条飞线了。要做到这一点,比较简单的实现是在保存好的 \(u\) 的括号序上继续走直到对应的飞线点(图中 \(u\) 的另一端)。
但这样又会有遍历多次的问题,可能某些连通块只覆盖了两次,而某些大连通块可能足足有十几次。但如果按照飞出点的 DFS 序遍历子结点,那整个括号序不会遍历超过两次。
同时需要记录飞入点,最后回到飞入点完成本次 DFS。
打包音频
直接把得到 signalXY 点列的两个坐标取出来,作为 wav 文件的左右声道。
注意由于播放率受限(比如笔者的声卡是 48kHz),如果 signalXY 太长,示波器可能显示不完整,需要适当压缩。比如一帧图片 2400 长度。
复制几份只是为了显示时间长一点。
void pack_signal(int m) {
int n = signalXY.size();
if (n == 0) return;
int height = grayMatrix.size();
int width = grayMatrix[0].size();
vector<int> compressed[2];
for (int i = 0; i < m; i++) {
int idx = int(1.0 * n / m * i + 0.5);
int x = signalXY[idx].first;
int y = signalXY[idx].second;
x = x * (1 << 16) / height - (1 << 15);
y = y * (1 << 16) / width - (1 << 15);
compressed[0].push_back(x);
compressed[1].push_back(y);
}
vector<int> copy_compressed[2];
copy_compressed[0] = compressed[0];
copy_compressed[1] = compressed[1];
for (int i = 0; i < 24; i++) {
copy_compressed[0].insert(copy_compressed[0].end(), compressed[0].begin(), compressed[0].end());
copy_compressed[1].insert(copy_compressed[1].end(), compressed[1].begin(), compressed[1].end());
}
createStereoWAV(copy_compressed[0], copy_compressed[1], 48000, BitDepth::BIT_16, "play.wav");
}
半成品效果
示波器没到。
示波器到了,但是效果很差,测了下声卡输出的信号不太行,一直有蜜汁高频振荡。
试了下用 STM32F03VET6 单片机的双路 DAC,能看个大概,但是飞线很乱,还有奇怪的毛刺。
但是示波器模拟器表现挺好的,怪。
破案了,单片机 DAC 没用 Buffer。加了就搞定了。
其实是 DAC 配置放到了定时器启动后面,然后先配置 X 信号再配置 Y,会有错位,图像这样就会乱掉。
成品(Canny 边缘检测用的双阈值是 0.02 和 0.01):

完整方案
几天后买了个新板子,用的 STM32H750VBT6 主控。

优点是工作主频更高(480MHz),存储空间更大(一次可以处理 60000 个点,而前面的 f103 只能做到 4000 左右,使用双缓冲可以做到翻倍),以及 SD 卡读写 DMA 不会通道不够用(DAC 两个通道都用了 DMA)。
然后我将坐标信息压到一个 play.bin 中,单片机读取 SD 卡的 play.bin,直接把数据搬到 DAC 的两个 DMA 中。
DAC 这边配置了 3MHz 的采样频率,平衡了输出信号质量和帧率上限。
项目
相关的项目源码放在了我的 github 仓库:https://github.com/LiceWx/oscilloShow
尝试跑了最基础(因为对边缘检测和 DAC 精度要求并不高)的 Bad Apple:https://github.com/LiceWx/oscilloShow/blob/main/bad apple.MP4




 浙公网安备 33010602011771号
浙公网安备 33010602011771号