补题
C. Min Max Sort
正难则反。
在操作中(1,n)一定是最后一次归位的,以此类推(2,n-1)是倒数第二次归位...
如果 \(k\) 次操作能时序列复原,则 \(k+1\)~\(n-k\) 在初始数列中的相对位置是正确的。
农场道路修建
与没有上司的舞会类似,关键在于添加道路。
添加的道路一定是两点中一有一无或两无,则判断哪些点必须有,用总方案数减去不合法方案数即可。
P7828 [CCO2021] Swap Swap Sort
基本思路不难,没有想到根号分治(准确来说是不会,呃呃),以及在 \(x\) 确定的情况下不会 \(O(n)\) 处理 \((x,y)\)。(\((x,y)\) 表示每个 \(x\) 前 \(y\) 的个数之和)
每次更新 \(ans\) 涉及 \((x,y)\) 和 \((y,x)\),可知 \(\underline{ cnt_x\times cnt_y=(x,y)+(y,x)}\) 。
根号分治:
根据 \(cnt\) 的大小,选择不同的统计 \((x,y)\) 的方式。(对于一种 \(cnt\),最多出现 \(\frac{n}{cnt}\) 次)
-
\(cnt_x\) 和 \(cnt_y\) 均较小时,直接暴力枚举 \(x\),\(y\) 出现的位置,统计答案即可;
复杂度 \(O(cnt\times q)\) -
存在 \(cnt\) 较大时:
复杂度 \(O(n\times \frac{n}{cnt})\)- \(cnt_x\) 较大时,将询问存储在 \(x\) 上,离线 \(O(n)\) 处理所有 \((x,y')\),然后 \(O(1)\) 获取询问的 \((x,y)\);
- \(cnt_y\) 较大时,将询问存储在 \(y\) 上,离线 \(O(n)\) 处理所有 \((x',y)\),然后 \(O(1)\) 获取询问的 \((x,y)\);
总复杂度 \(O(cnt\times q+n\times \frac{n}{cnt})\)
根据基本不等式 \(cnt=\frac{n}{\sqrt{q}}\) 时复杂最优,即 \(cnt=100\) 为界限。
P7832 [CCO2021] Bread First Search
本题要注意的是,对于那些不能转移的点,我们不应更新它的 \(dp\) 值,所以一开始将 \(dp_1\) 保留为 \(inf\),去判断哪些点不能被转移。
抉择
考虑 \(a_i\) 从 \(a_j\) 转移,若存在 \(a_k(j<k<i)\) 满足三者同样在二进制表示的第 \(x\) 位为 1(且 \(x\) 为最高位),则选上 \(a_k\) 一定更优,因为 \((a_j,a_k,a_i)\) 的值大于等于 \(2\cdot 2^x\) ,而 \((a_j,a_i)\) 的值不超过 \(2\cdot 2^x\)。因此,开一个 \(mp\) 数组,记录第 \(x\) 位作为最高位最后出现的位置,每次转移的时候枚举最高位即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1000100;
int mp[100];
ll dp[maxn],a[maxn],ans;
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
for(int j=0;j<50;j++){
dp[i]=max(dp[i],dp[mp[j]]+(a[mp[j]]&a[i]));
}
for(int j=49;j>=0;j--){
if((a[i]>>j)&1){
mp[j]=i;
break;
}
}
ans=max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}
备餐
将 \(a_i\) 按前缀划分成若干组(即二进制表示中高于 \(x\) 最高位的部分),易知每组中任意两数异或,前缀部分将变成零。易知每组中最多选 2 个数,因为:
所以每组的方案数 \(=\) 一个都不选的方案数 \(+\) 选一个的方案数 \(+\) 选两个的方案数。
总方案数 = 各组方案数的乘积 \(-1\)(减去空集)。
可以使用 \(01Tire\) 维护:
对于当前数 \(a\), 该组中,之前的数与其异或起来大于等于 \(x\) 的数目之和,为改组选两个的方案数。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=3e5+10;
int n,mod=998244353;
int sz[maxn*62],tr[maxn*62][2],up,tot,cnt;
ll x,ans=1,res;
map<ll,ll> mp;
vector<ll> vec[maxn];
void add(ll &aa,ll b){
// b%=mod;
aa+=b;
if(aa>=mod) aa-=mod;
}
void query(ll a){
int u=0;
for(int i=up;i>=0;i--){
int id=((a>>i)&1);
int y=((x>>i)&1);
if(y){
if(!tr[u][!id]) return;
else u=tr[u][!id];
}else{
if(tr[u][!id]) add(res,sz[tr[u][!id]]);
if(!tr[u][id]) return;
u=tr[u][id];
}
}
add(res,sz[u]);
}
void insert(ll a){
int u=0;
for(int i=up;i>=0;i--){
int id=((a>>i)&1);
if(!tr[u][id]) tr[u][id]=++tot;
u=tr[u][id];
sz[u]++;
}
}
void ini(){
for(int i=0;i<=tot;i++){
sz[i]=0;tr[i][0]=tr[i][1]=0;
}
tot=0;
}
int main(){
freopen("quin.in","r",stdin);
freopen("quin.out","w",stdout);
cin>>n>>x;
up=__lg(x);
if(x==0) up=-1;
for(int i=1;i<=n;i++){
ll a;cin>>a;
ll y=(a>>(up+1));
if(!mp[y]) mp[y]=++cnt;
vec[mp[y]].push_back(a);
}
for(int i=1;i<=cnt;i++){
ini();
res=vec[i].size()+1;
for(auto it:vec[i]){
query(it);
insert(it);
}
// cout<<res<<endl;
ans=ans*res%mod;
}
ans--;
if(ans<0) ans+=mod;
cout<<ans<<endl;
return 0;
}
约翰:奶牛杀手
没有想到建图,找二元环,悲。
若 \(x_i\) 被 \(j\) 的 \(l\) 和 \(r\) 给覆盖,则建一条从 \(j\) 向 \(i\) 的边。然后拓扑排序。
只能复活一次,代表着图上只能有一个环。易证,当三元环存在时,二元环一定存在(可以自己想一下),所以只需判断二元环即可,因为比较简单。
一开始还在想怎么建图,后来膜了佬的代码后,发现根本不用建图。
存在二元环的条件:\(l_j \le x_i<x_j\le r_i\) 。
因为输入保证 \(x\) 单调递增,所以选择用来判断的 \(r\) 越大越好,可以维护一个单调栈,顺便在出栈的时候判断一下条件即可。
找到环后删去该点,若仍存在环,则不能通过。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e6+10;
int n,st[maxn],top;
struct P{
int x,l,r;
}p[maxn];
int work(int x){
top=0;
for(int i=1;i<=n;i++){
if(i==x) continue;
while(top>0){
if(p[st[top]].r>=p[i].x&&p[i].l<=p[st[top]].x) return i;
if(p[st[top]].r>p[i].r) break;
top--;
}
// if(p[st[top]].x<=p[i].l) return i;
// while(top>0&&p[st[top]].r<=p[i].r){
// if(p[st[top]].r>=p[i].x&&p[i].l<=p[st[top]].x) return i;
// top--;
// }
// if(p[st[top]].r>=p[i].x&&p[i].l<=p[st[top]].x) return i;
st[++top]=i;
}
return 0;
}
int main(){
freopen("sekiro.in","r",stdin);
freopen("sekiro.out","w",stdout);
std::ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i].x>>p[i].l>>p[i].r;
}
int tmp=work(0);
if(tmp==0||work(tmp)==0) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}
flandre
将数组排序后,倒序枚举,计算以 \(i\) 为开头的答案: \(ans\ += a_i+num\cdot k\),\(num\) 为 \(a_j > a_i\) 的个数。
取最大值即为答案,方案为 \(i\) 至 \(n\)。(\(i\):取 \(i\) 时答案最大)
scarlet
哈希冲突的加强版。
\(x\) 比较大时,直接区间修改,区间查询即可;
\(x\) 比较小时:
序列被 \(x\) 划分成若干段,修改时,对每段的贡献是一样的,所以可以暴力记录 \(\mod x =y\) 需要增加的值并求前缀和,查询时把整段的贡献直接加上,散的部分求区间和。
19/10/2023
最近有点考得小爆炸,每次都把屎糊上去了,,,呃呃
gcd
倒着枚举 \(gcd\) ,然后 \(log\) 的复杂的枚举其倍数,找到第一个个数大于 \(k\) 的即为答案。
对于会不会出现枚举的倍数不互质(如 \(2gcd,4gcd,8gcd\) 这样的):不会,因为 \(gcd\) 是倒着枚举的,在枚举到 \(2gcd\) 的时候就已经找到答案了。
mathematics
一眼并查集+转换距离,但细节弄错了,呃呃。
设 \(d_i\) 表示从父节点到 \(i\) 的距离(反着走为 \(-d_i\))
将 \(a-b=c\) 转换成从 \(a\) 走向 \(b\) 的距离为 \(c\)。
每次合并和查询的时候更新一下距离,然后...不好描述,看代码吧
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define mkp make_pair
#define ll long long
const int maxn=3e5+10;
int n,m,bcj[maxn];
string ans;
ll d[maxn];
int find(int x){
if(bcj[x]==x) return x;
// int fx=find(bcj[x]);
find(bcj[x]);
d[x]+=d[bcj[x]];
return bcj[x]=bcj[bcj[x]];
}
void ini(){
for(int i=1;i<=n;i++){
bcj[i]=i;
// d[i]=inf;
}
}
int main(){
freopen("mathematics.in","r",stdin);
freopen("mathematics.out","w",stdout);
cin>>n>>m;
ini();
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
int fa=find(a),fb=find(b);
if(fa!=fb){
ans+='R';
// uni(fa,fb);
bcj[fb]=fa;
d[fb]=c+d[a]-d[b];
}else if(d[b]-d[a]==c) ans+='R';
else ans+='W';
}
cout<<ans<<endl;
return 0;
}
assemblage
学习了 zyc 巨巨的思路和代码。
没有想到用并查集,不是很会处理每次加边时需要乘的点权和。
从小往大加边,所以点会被这些边划分成好几块。
注意到 \(n\) 的范围很小,所以可以状压DP,1 代表该条边已经加上。每次把没有加的边两端的点都放到一个集合里,处理完后开始枚举上一个状态(即枚举哪一条边是新加的),新的贡献就是该边的权值 \(\times\) 左边集合的点权和 \(\times\) 右边集合的点权和,取最小值。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,rt,cnt=1;
int bcj[50];
ll inf=1e18,w[50],ww[50],sz[50],sum,a[50],ans,dp[(1<<23)],s,now,num[(1<<23)];
struct P{
int x,y,id;
}e[50];
int get_num(int x){
int res=0;
while(x){
if(x&1) res++;
x>>=1;
}
return res;
}
int find(int x){
if(bcj[x]==x) return x;
return bcj[x]=find(bcj[x]);
}
int main(){
freopen("assemblage.in","r",stdin);
freopen("assemblage.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i];
}
n--;
s=(1<<n)-1;
for(int i=1;i<=n;i++){
int x,y;cin>>x>>y;
e[i]={x,y,i};
}
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+1+n);
for(int i=0;i<(1<<n);i++){
num[i]=get_num(i);
dp[i]=inf;
}
dp[0]=0;
for(int i=1;i<=s;i++){
int x,y;
for(int j=1;j<=n+1;j++) bcj[j]=j,ww[j]=w[j],sz[j]=1;
for(int j=0;j<n;j++){
if(((i>>j)&1)) continue;
x=e[j+1].x,y=e[j+1].y;
x=find(x);y=find(y);
if(sz[x]<sz[y]) swap(x,y);
bcj[y]=x;ww[x]+=ww[y];sz[x]+=sz[y];
}
for(int j=0;j<n;j++){
if(!((i>>j)&1)) continue;
x=e[j+1].x,y=e[j+1].y;
x=find(x);y=find(y);
dp[i]=min(dp[i],dp[i^(1<<j)]+ww[x]*ww[y]*a[num[i]]);
}
}
cout<<dp[s]<<endl;
return 0;
}
24/10/2023
T2 毛球发动特攻 发出了残酷的纽扣
一道简单的组合 + 容斥,然后我这个 shaber 考试的时候想的可复杂,补题的时候没预处理一些东西还 T 了好几次。
每次找一个极长子串,使得子串中的 \(1\) 恰好有 \(k\) 个,每次重复计算的是相邻两个子串重复部分的排列(易知,重复部分有 \(k-1\) 个 \(1\),因为找的是极长子串),减去这一段的排列数即可。
注意特判 \(k=0\) 和整个串中 \(1\) 的个数小于 \(k\) 的情况。
还要预处理阶乘和逆元。
预处理阶乘和逆元代码 \(\downarrow\):
点击查看代码
fac[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
inv[n]=ksm(fac[n],mod-2);
for(int i=n;i>=1;i--) inv[i-1]=inv[i]*i%mod;
25/10/2023
T1 书架
超级简单的维护链表,因为之前没写过链表,比赛的时候不敢写,然后写暴力,但是加了一个愚蠢的错误特判,结果 \(0\) 分。痛,太痛了。
关于复杂度:每次合并,最长不超过 \(n/2\),类似于启发式合并。
T2 切面包
原题目:切割冰片
总之就是超级不会写,想不到 \(DP\) 状态要怎么设置,怎么转移,思维还是不够。
关于本题:
设 \(dp[i][j]\) 表示 前 \(i\) 横边和前 \(j\) 条竖边且第 \(j\) 条竖边被第 \(i\) 条横边所拦截 构成的方案数,可以转移到 \(dp[k][j+1]\ (k\ge i 且 a_{k}\ge j+1 )\),为什么 \(k\) 不能小于 \(i\):因为如果 \(j\) 被 \(i\) 前面的一条边拦住,代表着前面的横边没有超过 \(j\),那么 \(j+1\) 一定不会被其截住。
考虑优化第二维:因为 \(l_i\) 一定要大于等于当前的第 \(j\) 条边,且 \(n\) 的范围很小,所以可以根据横线的左端点划分为 \(n\) 段。同一段内合法的 \(l_i\) 是一样的,然后就是一直求前缀和,求前缀和的前缀和,求前缀和的前缀和的前缀和......所以可以用到组合数优化。
26/10/2023
C. Strong Password
27/10/2023
T2 快乐交换
29/10/2023
D. Doremy's Connecting Plan
很容易想到贪心,但不知道证明方法和优先队列的判断条件。
贪心策略是都往 1 号点连。
证明:
假设存在 \(1<i<j\le n\) 此时 \(i,j\) 都未与 \(1\) 连,则有:
(2)+(3)-(1) 有:$2\cdot a_1 < c\cdot (i+j\cdot (1-i)) $,因为 \(c\cdot (i+j\cdot (1-i)) < 0\) 所以假设不成立,贪心策略正确。
使用优先队列时,以 \(i \cdot c-a_i\) 为第一关键字入队,从小到大取,并与 \(1\) 加边。
30/10/2023
T1 进步科学
一眼状压dp。(但是细节不会)
分析题目可知,不同子节点对同一父节点的影响是异或操作。
考虑节点间的相互影响,随着天数的增加,状态向后转移,那么在枚举的时候,从前面加入点,则不需要考虑影响的问题。
预处理出按下第 \(i\) 节点后 \(j\) 天的状态。在转移状态向前加点时,可以把当前状态理解为向后平移,因为无论何时按下一个点,它独自对父节点的影响是不会改变的。
状态的转移不一定是从前一天,可能是从前几天,因为有可能中间几天不按点。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=22;
int n,f[maxn],tag,p,s;
int state[maxn][maxn*2];
bool dp[maxn*2][(1<<18)];
vector<int> G[maxn];
void dfs(int now){
// cerr<<now<<endl;
for(int i=0;i<G[now].size();i++){
int to=G[now][i];
for(int j=0;j<40;j++) state[to][j+1]=(state[now][j]^(1<<(to-1)));
dfs(to);
}
}
void write(int x){
for(int i=1;i<=n;i++){
cout<<((x>>(i-1))&1)<<" ";
}
cout<<endl;
}
int main(){
freopen("decoration.in","r",stdin);
freopen("decoration.out","w",stdout);
cin>>n;
for(int i=2;i<=n;i++){
cin>>f[i];
G[f[i]].push_back(i);
}
s=(1<<n);
// cerr<<"done1"<<endl;
for(int i=1;i<=n;i++){
int x;cin>>x;
tag^=(x<<(i-1));
}
for(int i=1;i<=40;i++){
state[1][i]=1;
}
dfs(1);
// cerr<<"done2"<<endl;
dp[0][0]=1;
for(int dy=1;;dy++){
for(int now=0;now<s;now++){
for(int dd=0;dd<dy;dd++){
for(int j=1;j<=n;j++){
dp[dy][now^state[j][dy]]|=dp[dd][now];
}
}
}
if(dp[dy][tag]) return cout<<dy<<endl,0;
}
return 0;
}
31/10/2023
T2 LIS问题
(\(a[i]\) 代表原数列)
- 对于相同的 \(f[i]\) 从左到右,\(a[i]\) 一定递减;
- 对于 \(f[i],f[j](f[i]=f[j]+1且j<i)\),\(a[i]\) 一定至少比 \(a[j]\) 大一;
题目要求找到在所以合法的排列中,每个位置可能的最大值,我们只需考虑对于当前位置,有多少个数必须大于它即可(位于 \(i\) 前面 \(f[j]\) 与 \(f[i]\) 相等的数量 + 位于 \(i\) 后面必须大于 \(a[i]\) 的数量)。
存在限制关系时,考虑建图,定义边的含义:\(i \rightarrow j\) 表示 \(j\) 要大于 \(i\)。
然后是一些细节:
- 因为数据范围是 \(1e7\) 如果直接建边,边过多,会 TLE 也会 MLE。
对于样例 [1,1,2,1,3,4,4,2,5,3] 建出这样一个图:
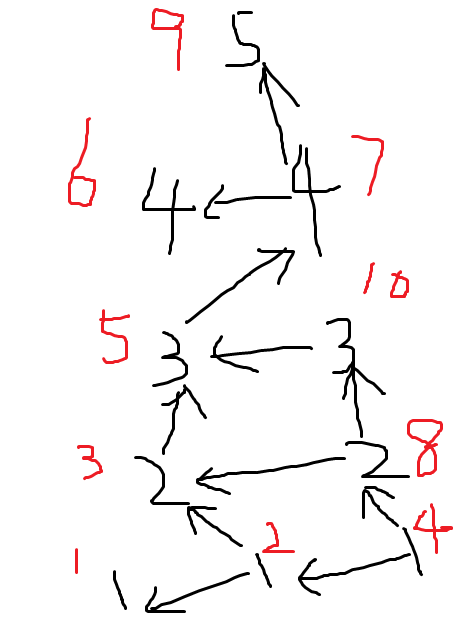
然后按照图从上倒下遍历即可。 - 设 \(dp[i]\) 表示大于点 \(i\) 的数量。值的转移:
- 对于没有出边的点 \(dp[i]=0\)(因为没有必须大于它的点);
- 有 \(up\) 的点 \(dp[i]=dp[up]+1+num_{left}\);
- 无 \(up\) 的点(即只有 \(left\))\(dp[i]=dp[left]+1\)(这种情况是我们经过上述的化简得到)。
- 如果需要排序,快排会 T,考虑桶排。
点击查看代码
#include<bits/stdc++.h>
using std::min;
using namespace std;
#define ll long long
static inline
int __my_rand (int *seed) {
*seed = *seed * 1103515245 + 12345;
return ((unsigned)*seed) / 34;
}
int gen (int N, int Lim, int seed, int* F) {
int cur = 0;
for (int i = 1; i <= N; i ++) {
int rd = __my_rand(&seed);
if (rd % std::min(10, cur + 1) == 0 && cur < Lim) F[i] = ++cur;
else F[i] = (__my_rand(&seed) % cur) + 1;
}
return 0;
}
const int maxn=1e7+10;
int n,lim,seed,f[maxn],dp[maxn];
int mod=998244353;
ll pw[maxn],bas=131,ans,mx;
struct P{
int x,y,num,id;//up left
}G[maxn];
int main() {
// freopen("lis.in","r",stdin);
// freopen("lis.out","w",stdout);
cin>>n>>lim>>seed;
gen(n,lim,seed,f);
/* for(int i=1;i<=n;i++){
cout<<f[i]<<" ";
mx=max(mx,1ll*f[i]);
}
cout<<endl;*/
vector<vector<int>> mp(mx+5);
pw[0]=1;
// cout<<"done"<<endl;
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*bas%mod;
// tmp[i]={f[i],i};
mp[f[i]].push_back(i);
}
for(int val=1;val<=mx;val++){
int p=0;
for(int i=0;i<mp[val].size();i++){
int id=mp[val][i];
G[id].id=id;
if(i!=0){
G[id].y=mp[val][i-1];
G[id].num=G[mp[val][i-1]].num+1;
}
int l=id,r=n;
if(i!=mp[val].size()-1) r=mp[val][i+1];
if(val==mx) continue;
while(p+1<mp[val+1].size()&&mp[val+1][p+1]<=r) p++;
if(mp[val+1][p]<l||mp[val+1][p]>r) continue;
G[id].x=mp[val+1][p];
}
}
// cout<<"id up left nu dp"<<endl;
for(int val=mx;val>=1;val--){
for(int i=0;i<mp[val].size();i++){
int id=mp[val][i];
int up=G[id].x,left=G[id].y,nu=G[id].num;
dp[id]=(up!=0)*(dp[up]+1+nu)+(up==0)*(dp[left]+1);
if(!up&&!left) dp[id]=0;
// cout<<id<<" "<<up<<" "<<left<<" "<<nu<<" "<<dp[id]<<endl;
}
}
// sort(G+1,G+1+n,cmp2);
for(int i=1;i<=n;i++){
// cout<<dp[i]<<" ";
int an=n-dp[i];
// cout<<an<<" ";
ans+=1ll*an*pw[i]%mod;
if(ans>=mod) ans-=mod;
}
// cout<<endl;
cout<<ans<<endl;
return 0;
}
03/11/2023
T1 笛卡尔树
对于一些数和一个形状固定的树,得到的树是唯一的,所以可以先确定树的形状,然后随机选一些数填上去。
将组合数拆开处理可以减少取模次数从而加快代码运行速度。
13/11/2023
T2 翻转道路
- 只有翻转最短路树上的边才会对原来的最短路产生影响
- 对于如何记录最短路树上的边:记录下边的 id
- 翻转代价不能直接加到边权上——可能会计算两次(实际上只需计算一次)
- 稠密图 dij 不加堆优化更优,用 map 会再次带上 log

