[模板] FFT 快速傅里叶变换
[模板] FFT 快速傅里叶变换
用来快速求多项式乘法的 \(\text O(nlogn)\) 算法。
概论
卷积:乘法的本质
形为 \(C[k]=\sum\limits_{i\ \oplus\ j=k}A[i]\cdot B[j]\) 的式子为卷积。
多项式乘法为加法卷积,即 \(C[k]=\sum\limits_{i\ +\ j=k}A[i]\cdot B[j]\) .
可以发现,直接求解是 \(\text O(n^2)\) 的。
复数乘法的 几何意义
模数相乘,辐角相加。(复平面)
单位复根(在复平面上定义)
我们称符合 \(x^n=1\) 在复数意义下的解是单位复根,这样的解有 \(n\) 个,用 \(w_n^k\) 表示 \((k\in [0,n-1],k\in Z)\) 。
注意:\(k\geq n\) 是可能的,等价于 \(k\ mod\ n\) 。
其中 \(w_n^k\) 的三角表示为 \(\cos(\frac{2\pi}{n}\cdot k)+\sin(\frac{2\pi}{n}\cdot k)\cdot i\) ,可以发现 \(n\) 个单位根均匀分布在单位元上。
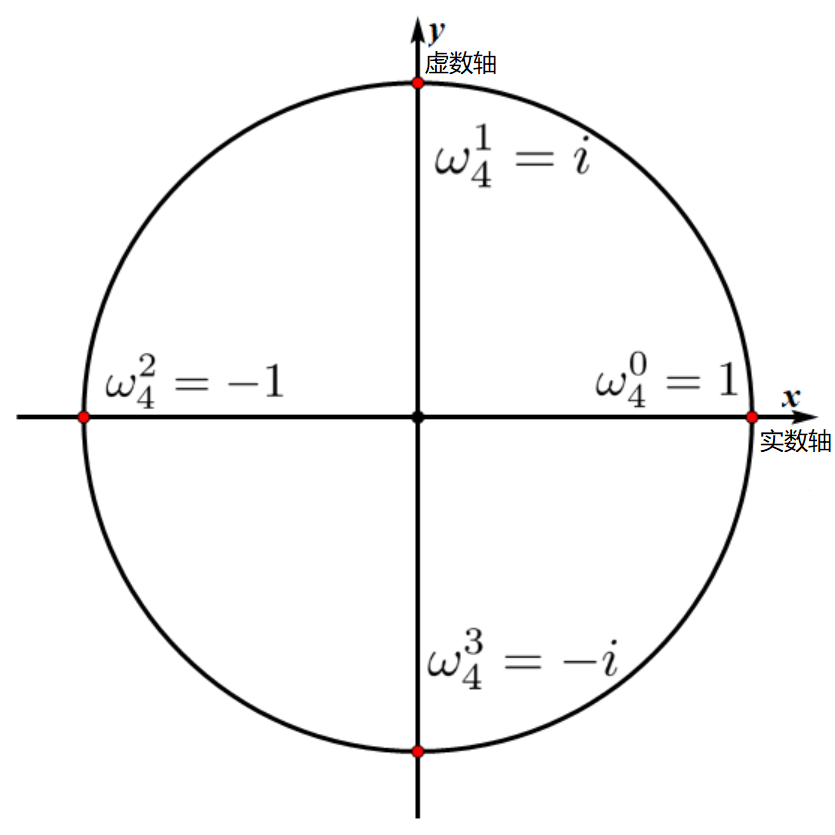
从 几何角度 理解单位根的性质:
-
\(w_n^n=1\),相当于 \(w_n^0=1\)。
-
\(w^k_n=w^{2k}_{2n}\) ,类似于切分圆盘,占比相等。
-
\(w_{2n}^{k+n}=-w_{2n}^k\),相当于关于原点对称。
快速傅里叶变换
基本思路
先进行一次 FFT 将两个函数的系数表示转化为点值表示。
根据两个函数 \(f(x)\) 和 \(g(x)\) 的点值表示 \(\text O(n)\) 地求得 \(f(x)\cdot g(x)\) 的点值表示,然后再 插值 回去。
关键步骤是将点值表示快速转化为系数表示,快速插值。
FFT 就是利用了单位根的特殊性质,通过分治加速运算。
其主要优化技巧是将各次项按照奇偶性分组,同时利用单位根的特殊性质简化递归计算。
奇偶性分组
对于 \(f(x)=a_0+a_1x+a_2x^2+\cdots+a_7x^7\)。
建立新函数 \(G(x)=a_0+a_2x+a_4x^2+a_6x^3\),\(H(x)=a_1+a_3x+a_5x^2+a_7x^3\)。
那么原函数 \(f(x)=G(x^2)+x\times H(x^2)\) 。
左边处理 \(G(x^2)\) ,右边处理 \(H(x^2)\) 。
单位根简化递归运算

也就是说,得到了左右两边的局部系数表示后,再计算当前的系数表示。
注意,在每次递归中,\(k\) 是一个相对位置。
蝴蝶变换
通过预处理出最后每个次项所处的位置,人工模拟从下往上合并的过程。
原来的递归版(数组下标,先偶后奇,从0开始):
0 1 2 3 4 5 6 7 第1层
0 2 4 6|1 3 5 7 第2层
0 4|2 6|1 5|3 7 第3层
0|4|2|6|1|5|3|7 第4层
最后的序列是原序列的二进制反转。
可以 \(\text O(n)\) 递推搞定。

可以手玩几个数,怎么证的还没发现。
for(int i=0;i<n;i++){
rev[i]=rev[i>>1]>>1;
if(i&1)rev[i]|=(n>>1);
}
由于分治过程,多项式项数必须为 \(2\) 的整次幂。
while(limit<n+m+1)limit<<=1;
然后就可以模拟合并过程了:
for(int mid=2;mid<=n;mid<<=1){//枚举当前需要合并层的大小
comp wn(cos(2.0*Pi/(1.0*mid)),op*sin(2.0*Pi/(1.0*mid)));//变化的幅度,理解成一个向量
for(int i=0;i<n;i+=mid){//每个地下一层区间的左端点
comp w(1,0);//1,w_n^0
for(int j=i;j<i+mid/2;j++,w*=wn){//遍历这个下一层区间的前半段,同时更新后半段
comp x=a[j],y=w*a[j+mid/2];//DFT左半边 & 右半边
a[j]=x+y;a[j+mid/2]=x-y;//相对位置,公式决定
}
}
}
总代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
T x=0;char ch=getchar();bool fl=false;
while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
}
return fl?-x:x;
}
#include <complex>//STL的复数,有实部和虚部
#include <cmath>//Pi
const int maxn = 1e7 + 10;
#define comp complex<double>
const double Pi=acos(-1.0);
comp F[maxn],G[maxn];
int rev[maxn],limit=1,n,m;
void FFT(comp *a,int n,int op){
for(int i=0;i<n;i++){
rev[i]=rev[i>>1]>>1;
if(i&1)rev[i]|=(n>>1);
}
for(int i=0;i<n;i++)if(i<rev[i])swap(a[rev[i]],a[i]);
for(int mid=2;mid<=n;mid<<=1){
comp wn(cos(2.0*Pi/(1.0*mid)),op*sin(2.0*Pi/(1.0*mid)));
for(int i=0;i<n;i+=mid){
comp w(1,0);
for(int j=i;j<i+mid/2;j++,w*=wn){
comp x=a[j],y=w*a[j+mid/2];
a[j]=x+y;a[j+mid/2]=x-y;
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++){
double x;scanf("%lf",&x);F[i].real(x);
}
for(int i=0;i<=m;i++){
double x;scanf("%lf",&x);G[i].real(x);
}
while(limit<n+m+1)limit<<=1;//limit>=n+m+1,n+m+1是卷积后项的个数,<limit相当于<=n+m
FFT(F,limit,1);FFT(G,limit,1);//计算点值表示
for(int i=0;i<limit;i++)F[i]=F[i]*G[i];
FFT(F,limit,-1);//插值回去
for(int i=0;i<=n+m;i++)printf("%d ",(int)(F[i].real()/limit+0.5));
puts("");
return 0;
}
FFT优化高精乘法
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
template <typename T>
inline T read(){
T x=0;char ch=getchar();bool fl=false;
while(!isdigit(ch)){if(ch=='-')fl=true;ch=getchar();}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+(ch^48);ch=getchar();
}
return fl?-x:x;
}
#include <complex>
#include <cmath>
#define int long long
#define comp complex<double>
const int maxn = 1e7 + 100;
const double Pi=acos(-1.0);
comp F[maxn],G[maxn];
char s[maxn>>1],t[maxn>>1];
int n,m,ans[maxn],rev[maxn],limit=1;
void FFT(comp *A,int n,int op){
for(int i=0;i<n;i++){
rev[i]=rev[i>>1]>>1;
if(i&1)rev[i]|=(n>>1);
}
for(int i=0;i<n;i++)if(i<rev[i])swap(A[i],A[rev[i]]);
for(int mid=2;mid<=n;mid<<=1){
comp wn(cos(2.0*Pi/(1.0*mid)),sin(2.0*Pi*op/(1.0*mid)));
for(int i=0;i<n;i+=mid){
comp w(1,0);
for(int j=i;j<i+mid/2;j++){
comp x=A[j],y=A[j+mid/2]*w;
A[j]=x+y;A[j+mid/2]=x-y;
w*=wn;
}
}
}
}
int main(){
scanf("%s%s",s,t);
n=strlen(s),m=strlen(t);n--;m--;
for(int i=0;i<=n;i++)F[i].real((double)(s[n-i]-'0'));
for(int i=0;i<=m;i++)G[i].real((double)(t[m-i]-'0'));
while(limit<n+m+1)limit<<=1;
FFT(F,limit,1);FFT(G,limit,1);
for(int i=0;i<limit;i++)F[i]=F[i]*G[i];
FFT(F,limit,-1);
for(int i=0;i<=n+m;i++)ans[i]=(int)(F[i].real()/limit+0.5);
int pos=n+m;
for(int i=0;i<=n+m || ans[i];i++){
if(ans[i]>=10){
ans[i+1]+=ans[i]/10;
ans[i]%=10;
}
pos=max(pos,i);
}
for(int i=pos;i>=0;i--)printf("%lld",ans[i]);puts("");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号