关于红黑树(R-B tree)原理,看这篇如何
学过数据数据结构都知道二叉树的概念,而又有多种比较常见的二叉树类型,比如完全二叉树、满二叉树、二叉搜索树、均衡二叉树、完美二叉树等;今天我们要说的红黑树就是就是一颗非严格均衡的二叉树,均衡二叉树又是在二叉搜索树的基础上增加了自动维持平衡的性质,插入、搜索、删除的效率都比较高。红黑树也是实现TreeMap存储结构的基石。
一. 二叉搜索树
二叉搜索树又叫二叉查找树、二叉排序树,我们先看一下典型的二叉搜索树,这样的二叉树有何规则特点呢?
- 节点的左子树小于节点本身;
- 节点的右子树大于节点本身;
- 左右子树同样为二叉搜索树;
下图就是一颗典型的二叉搜索树
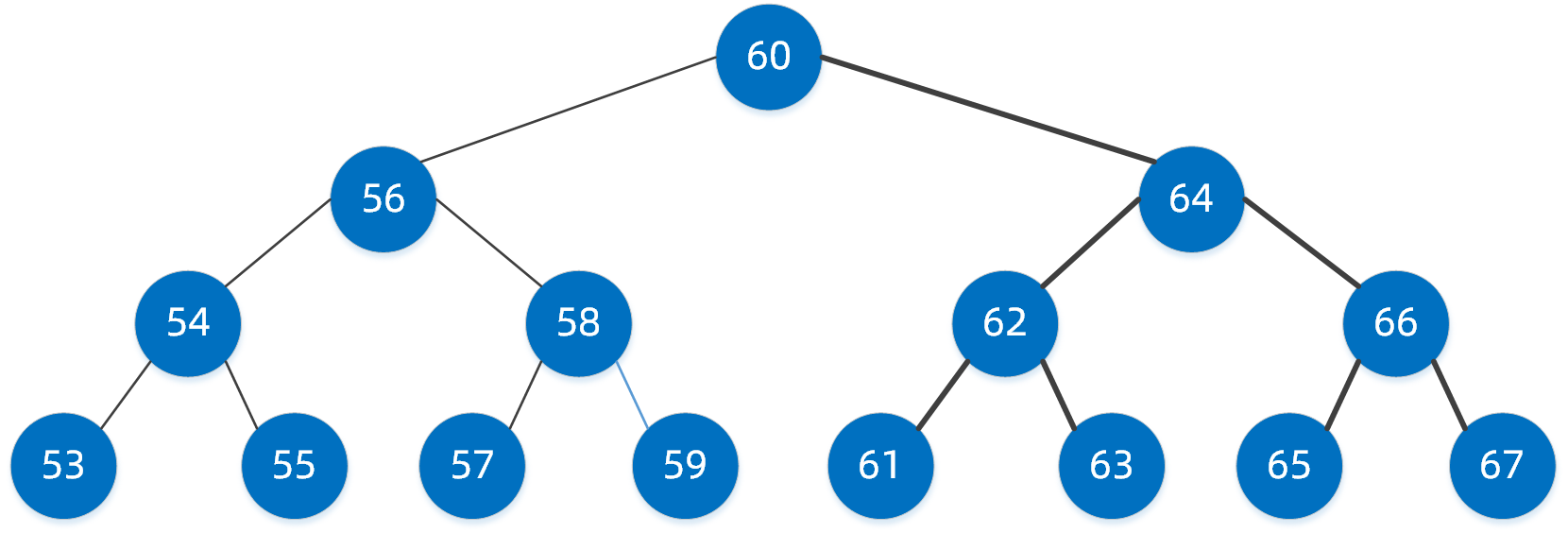
二叉搜索树是均衡二叉树的基础,我们看一下它的搜索步骤如何
我们要从二叉树中找到值为 58 的节点
第一步:首先查找到根节点,值为60的节点
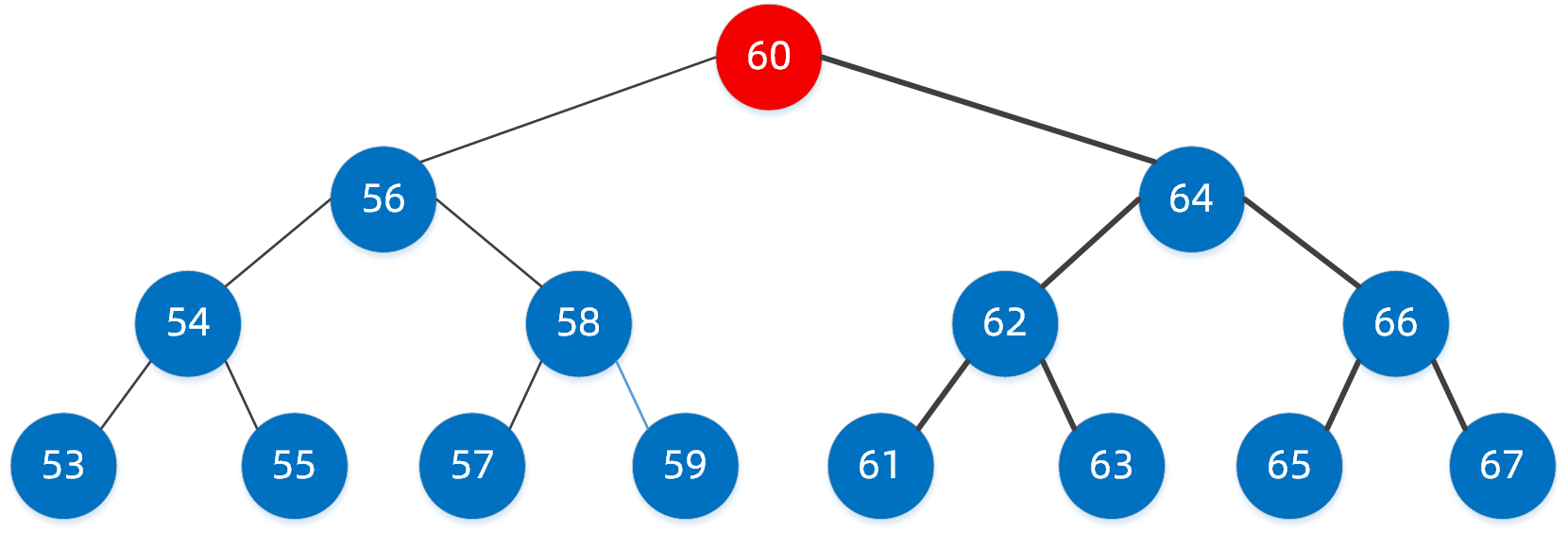
第二步:比较我们要找的值58与该节点的大小
如果等于,那么恭喜,已经找到;
如果小于,继续找左子树;
如果大于,那么找右子树;
很明显58 < 60,因此我们找到左子树的节点 56,此时我们已经定位到了节点56
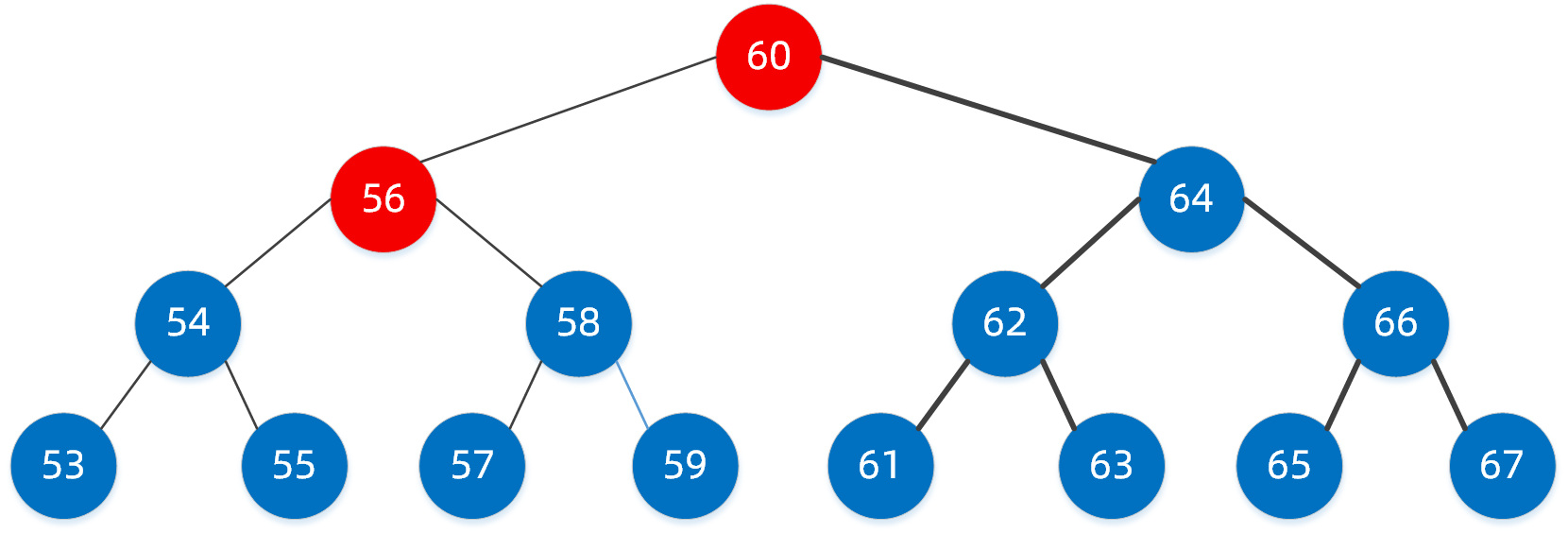
第三步:按照第二步的规则继续找
58 > 56 我们需要继续找右子树,定位到了右子树节点58,恭喜,此时我们已经找到了。
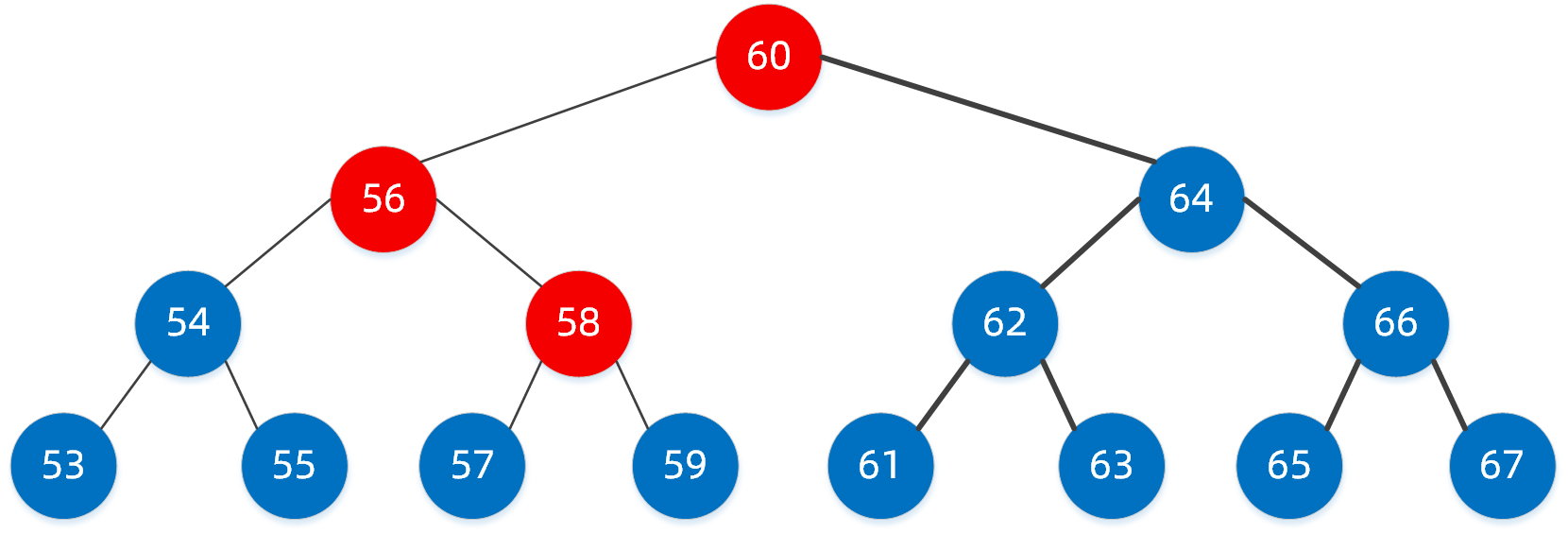
我们经过三步就已经找到了,其实就是我们平时所说的二分查找,这种二叉搜索树好像查找效率很高,但同样它也有缺陷,如下面这样的二叉搜索树。
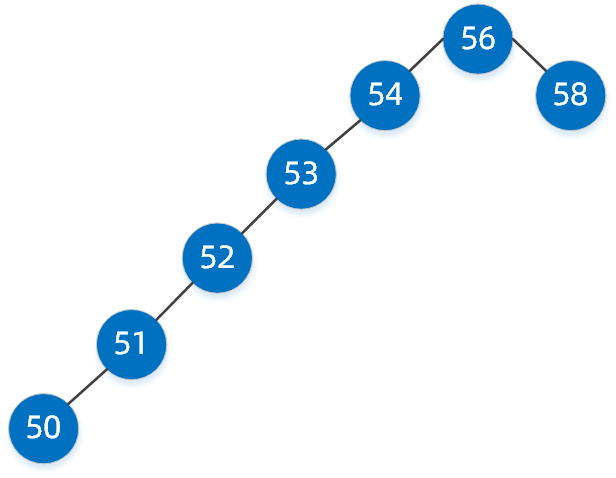
看到这样的二叉搜索树是否很别扭,典型的大长腿瘸子,但它也是二叉搜索树,如果我们要找值为50的节点,基本上和单链表查询没多大区别了,性能将大打折扣。这个时候我们的均衡二叉树就粉墨登场了,均衡二叉树就是在二叉搜索树的基础上添加了自动维持平衡的性质。
上面的大长腿瘸子二叉搜索树经过自动平衡后,可能就成为了下面这样的二叉树。

经过了自动平衡,再去找值为50的节点,查找性能将提升很多。红黑树就是非严格均衡的二叉搜索树。
二. 红黑树规则特点
红黑树具体有哪些规则特点呢?
- 节点分为红色或者黑色;
- 根节点必为黑色;
- 叶子节点都为黑色,且为null;
- 连接红色节点的两个子节点都为黑色(红黑树不会出现相邻的红色节点);
- 从任意节点出发,到其每个叶子节点的路径中包含相同数量的黑色节点;
- 新加入到红黑树的节点为红色节点;
规则看着好像挺多,没错,因为红黑树也是均衡二叉树,需要具备自动维持平衡的性质,上面的6条就是红黑树给出的自动维持平衡所需要具备的规则
我们看一看一个典型的红黑树到底是什么样儿?
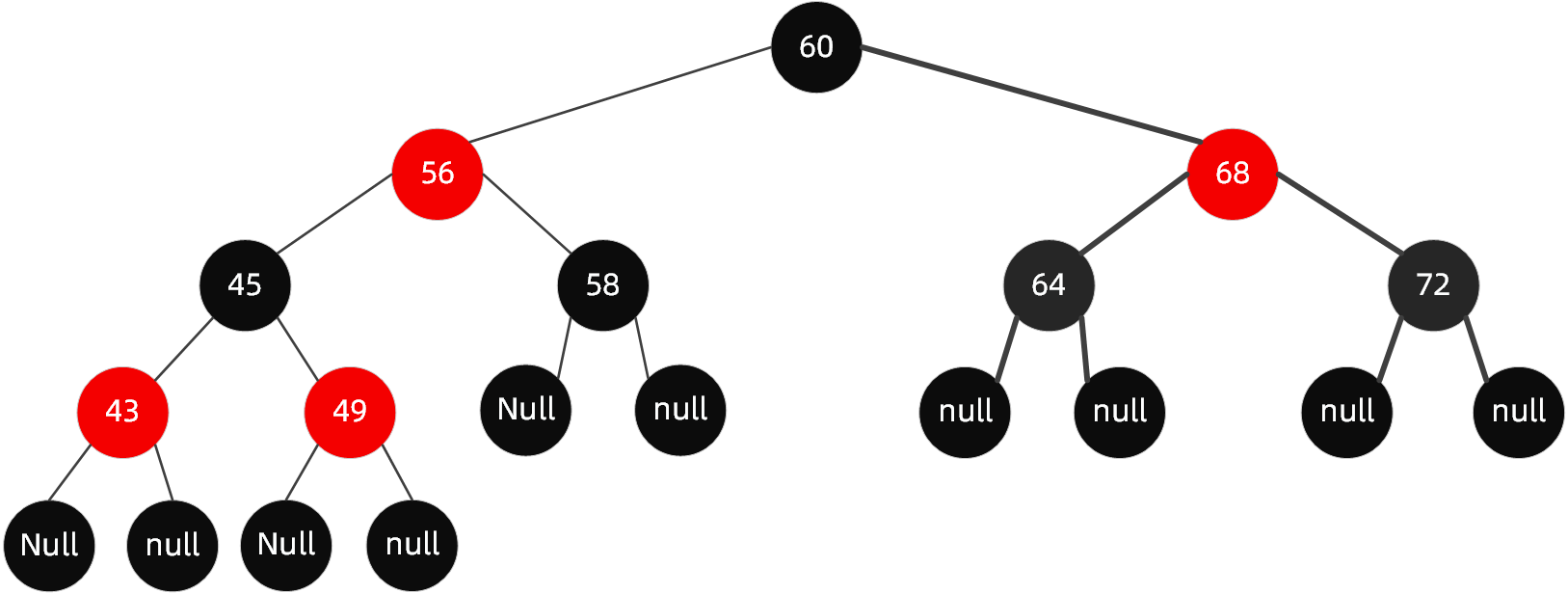
首先解读一下规则,除了字面上看到的意思,还隐藏了哪些意思呢?
第一. 从根节点到叶子节点的最长路径不大于最短路径的2倍
怎么样的路径算最短路径?
从规则5中,我们知道从根节点到每个叶子节点的黑色节点数量是一样的,那么纯由黑色节点组成的路径就是最短路径;
什么样的路径算是最长路径?
根据规则4和规则3,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点数量相同时,就是最长路径,也就是黑色节点(或红色节点)* 2
第二. 为什么说新加入到红黑树中的节点为红色节点
从规则4中知道,当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的,此时假如新的黑色节点的话,必然破坏规则,但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些,下面我们也会举例来说明。
什么情况下,红黑树的结构会被破坏呢?破坏后又怎么维持平衡,维持平衡主要通过两种方式【变色】和【旋转】,【旋转】又分【左旋】和【右旋】,两种方式可相互结合。
下面我们从插入和删除两种场景来举例说明
三. 红黑树节点插入
当我们插入值为66的节点时,红黑树变成了这样
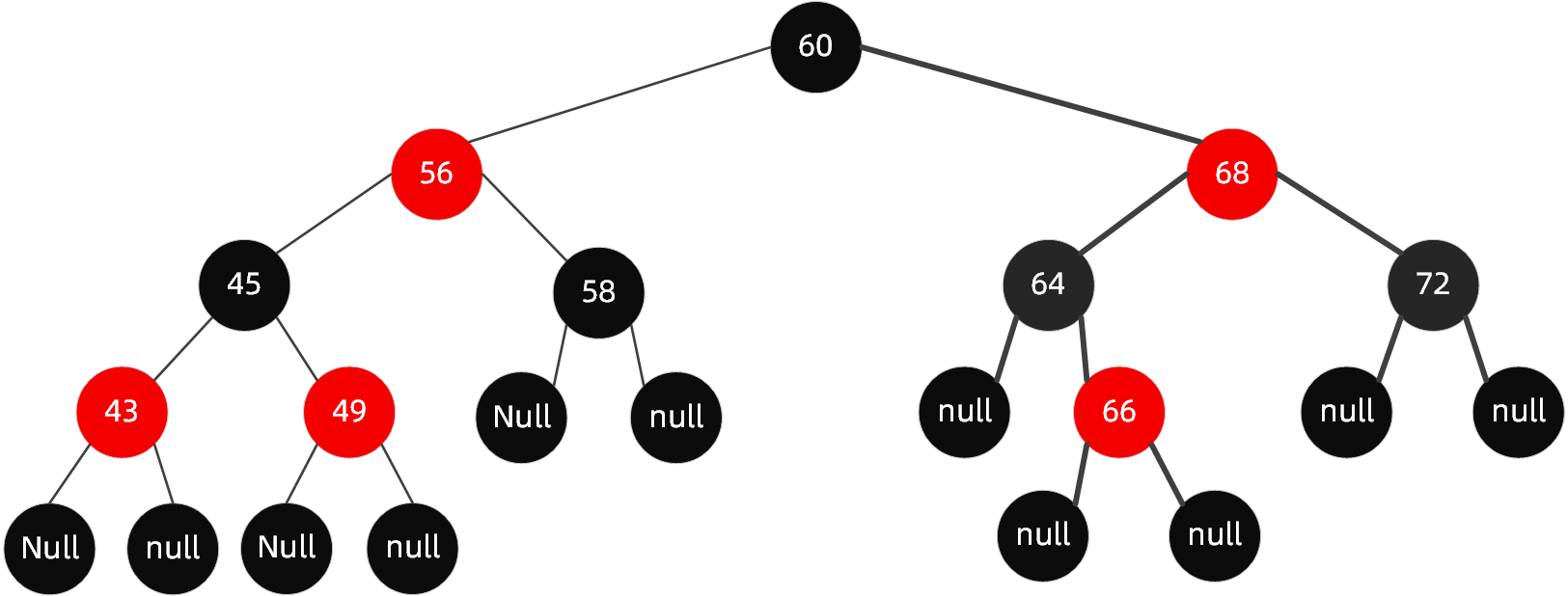
很明显,这个时候结构依然遵循着上述6大规则,无需启动自动平衡机制调整节点平衡状态;
如果再向里面插入值为51的节点呢,这个时候红黑树变成了这样
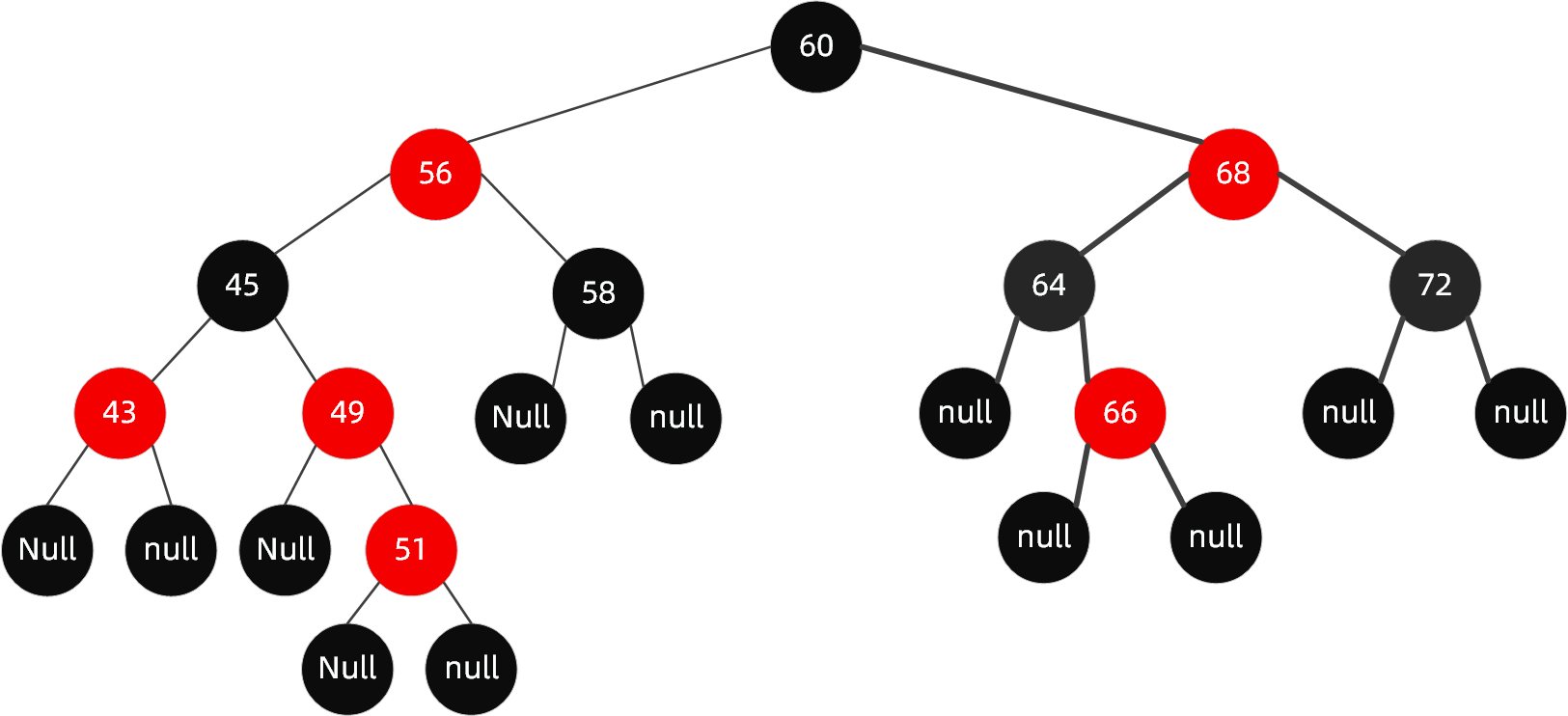
很明显现在的结构不遵循规则 4 了,这个时候就需要启动自动平衡机制调整节点平衡状态
3.1 变色
我们可以通过变色的方式,使结构满足红黑树的规则
- 首先解决结构不遵循规则 4 这一点(红色节点相连,节点49-51),需将节点49改为黑色;
- 此时我们发现又违反了规则5(56-49-51-XX路径中黑色节点超过了其他路径),那么我们将节点45改为红色节点;
- 哈哈,妹的,又违反了规则4(红色节点相连,节点56-45-43),那么我们将节点56和节点43改为黑色节点;
- 但是我们发现此时又违反了规则5(60-56-XX路径的黑色节点比60-68-XX的黑色节点多),因此我们需要调整节点68为黑色;
- 完成!!
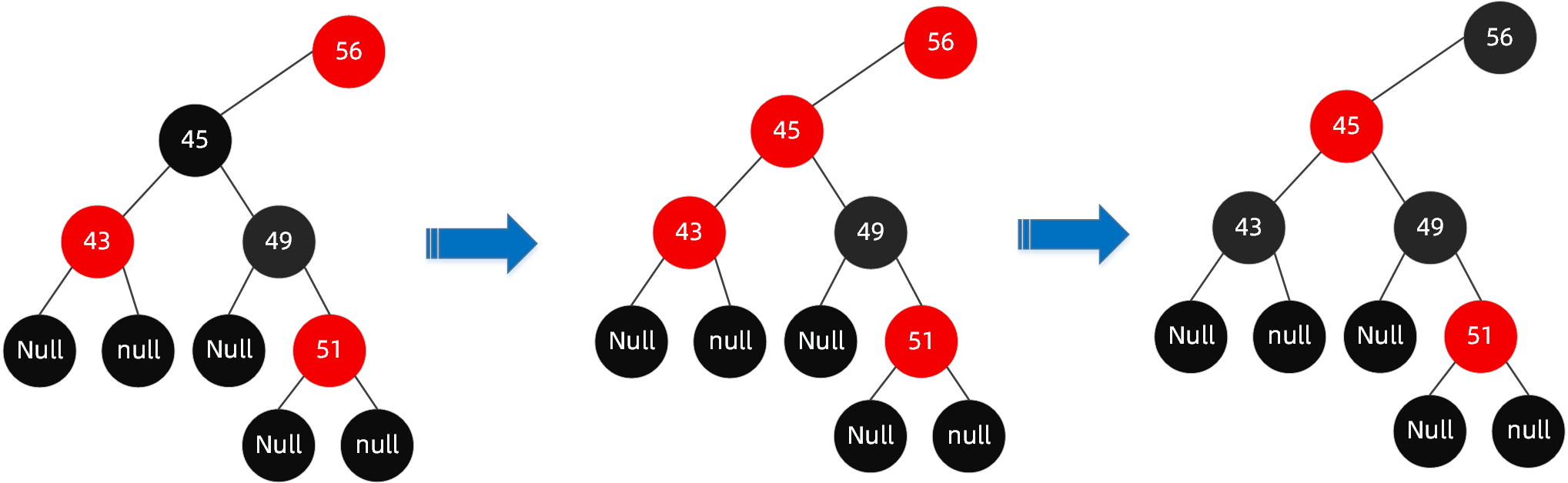
最终调整完成后的树为:
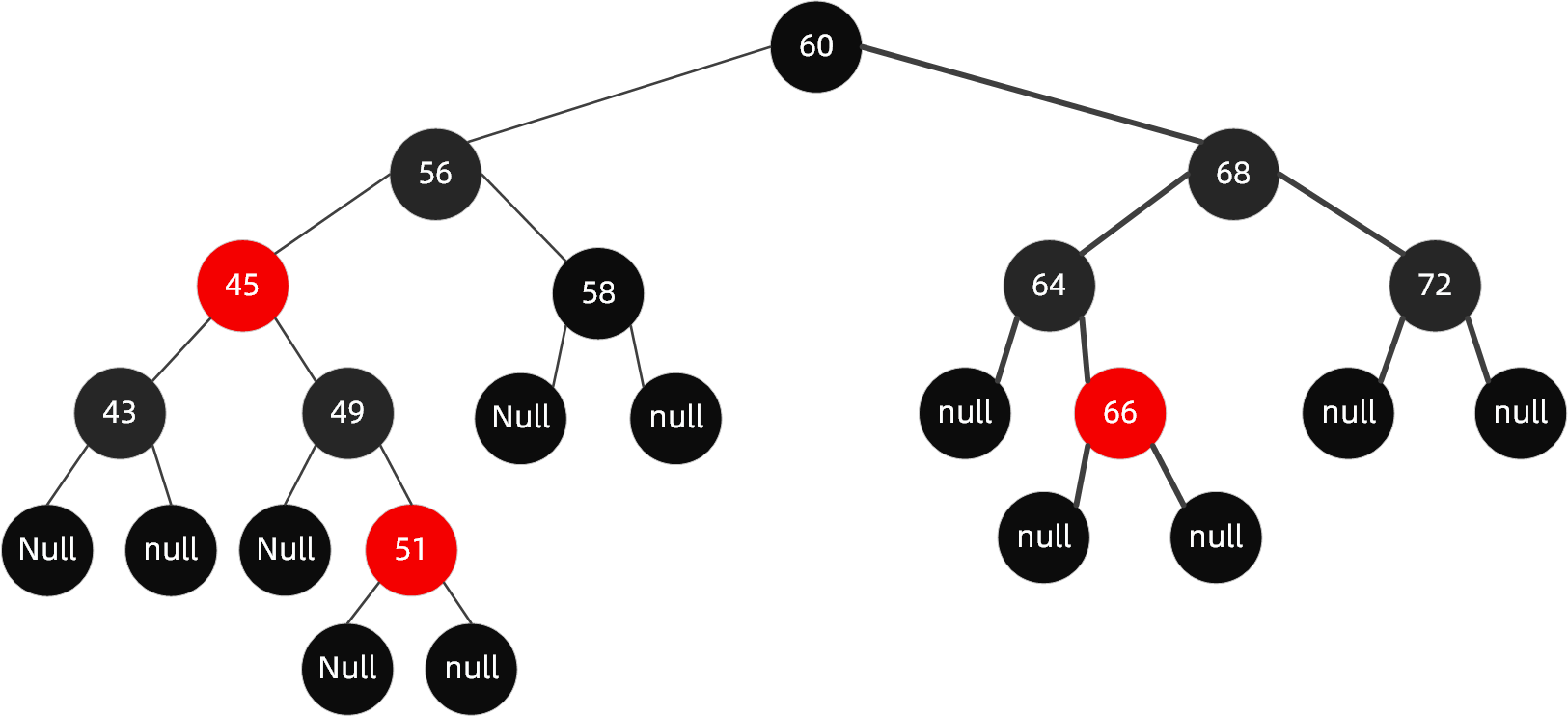
但并不是什么时候都那么幸运,可以直接通过变色就达成目的,大多数时候还需要通过旋转来解决。
如在下面这棵树的基础上,加入节点65.
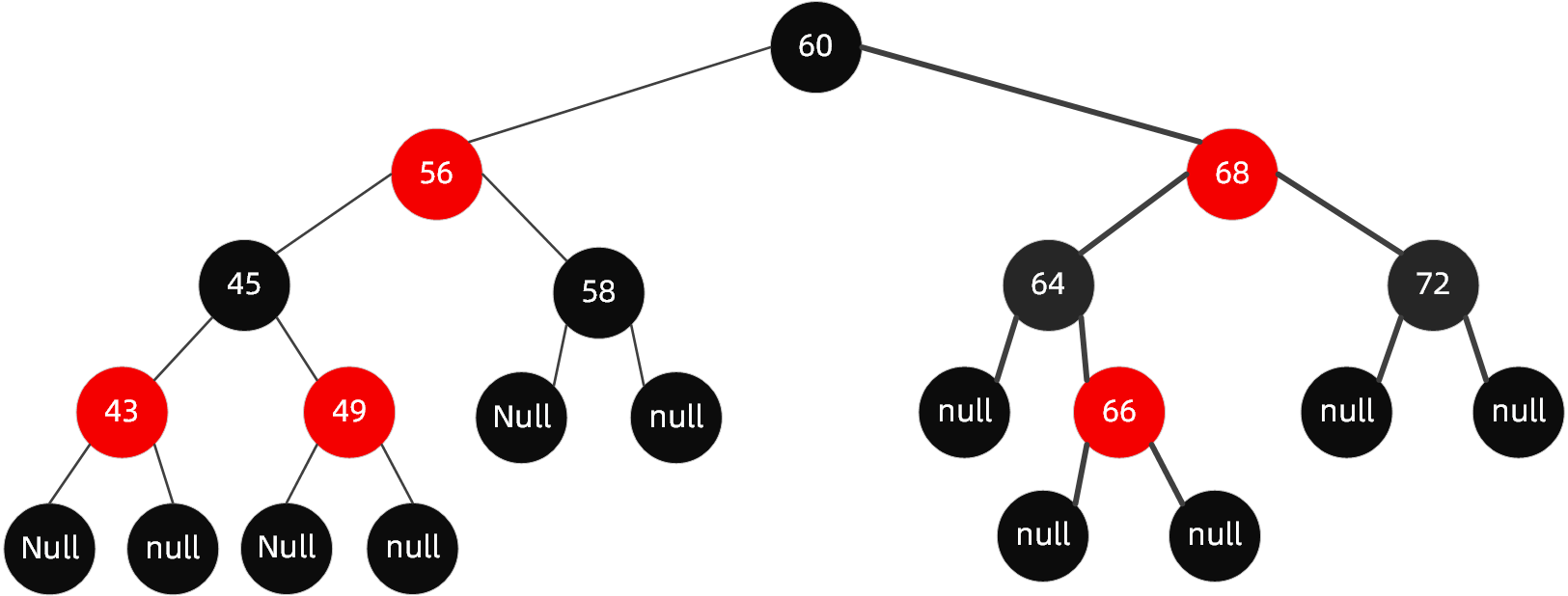
插入节点65后进行以下步骤
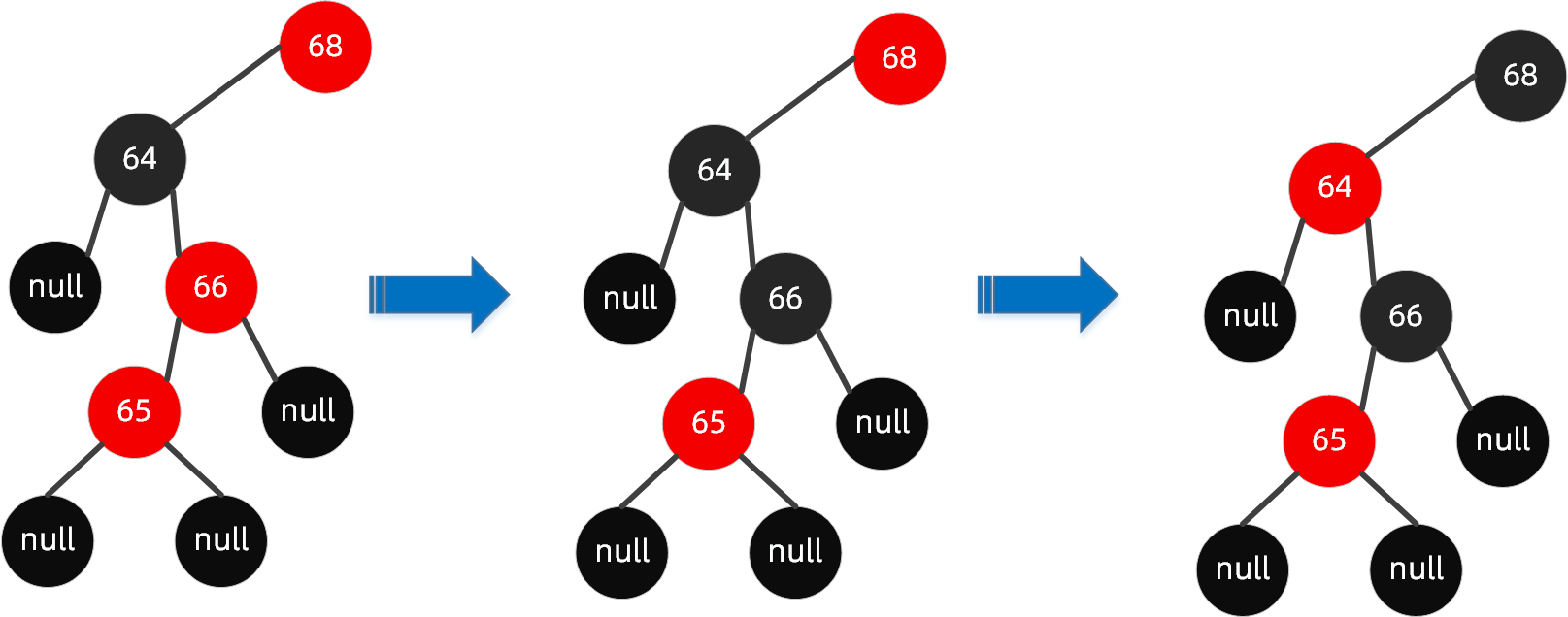
这个时候,你会发现对于节点64无论是红色节点还是黑色节点,都会违反规则5,路径中的黑色节点始终无法达成一致,这个时候仅通过【变色】已经无法达成目的。我们需要通过旋转操作,当然【旋转】操作一般还需要搭配【变色】操作。
旋转包括【左旋】和【右旋】,
左旋:
逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点
左旋操作步骤如下:
首先断开节点PL与右子节点G的关系,同时将其右子节点的引用指向节点C2;然后断开节点G与左子节点C2的关系,同时将G的左子节点的应用指向节点PL

右旋:
顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点
右旋操作步骤如下:
首先断开节点G与左子节点PL的关系,同时将其左子节点的引用指向节点C2;然后断开节点PL与右子节点C2的关系,同时将PL的右子节点的应用指向节点G

无法通过变色而进行旋转的场景分为以下四种:
3.2 左左节点旋转
这种情况下,父节点和插入的节点都是左节点,如下图(旋转原始图1)这种情况下,我们要插入节点65
规则如下:以祖父节点【右旋】,搭配【变色】
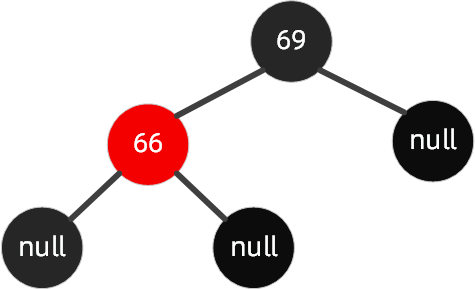
按照规则,步骤如下:
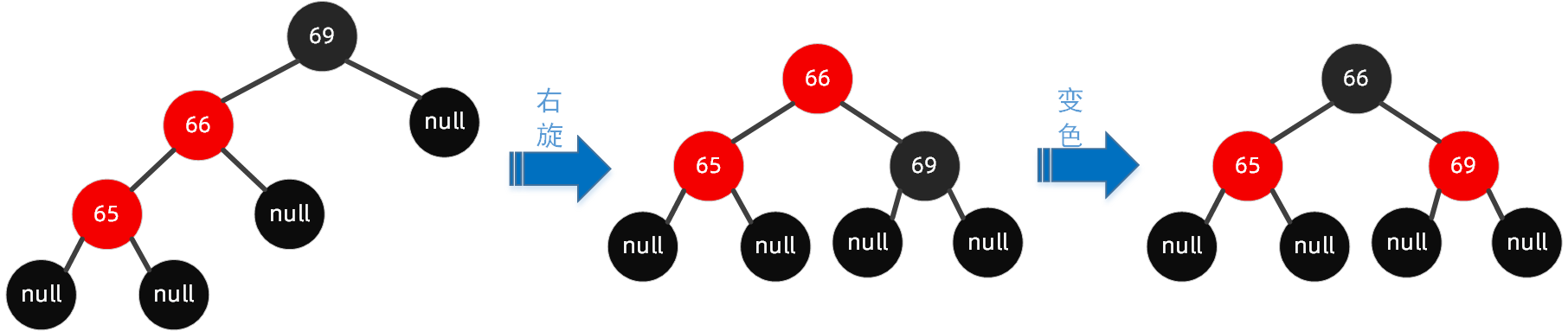
3.3 左右节点旋转
这种情况下,父节点是左节点,插入的节点是右节点,在旋转原始图1中,我们要插入节点67
规则如下:先父节点【左旋】,然后祖父节点【右旋】,搭配【变色】
按照规则,步骤如下:

3.4 右左节点旋转
这种情况下,父节点是右节点,插入的节点是左节点,如下图(旋转原始图2)这种情况,我们要插入节点68
规则如下:先父节点【右旋】,然后祖父节点【左旋】,搭配【变色】

按照规则,步骤如下:

3.5 右右节点旋转
这种情况下,父节点和插入的节点都是右节点,在旋转原始图2中,我们要插入节点70
规则如下:以祖父节点【左旋】,搭配【变色】
按照规则,步骤如下:
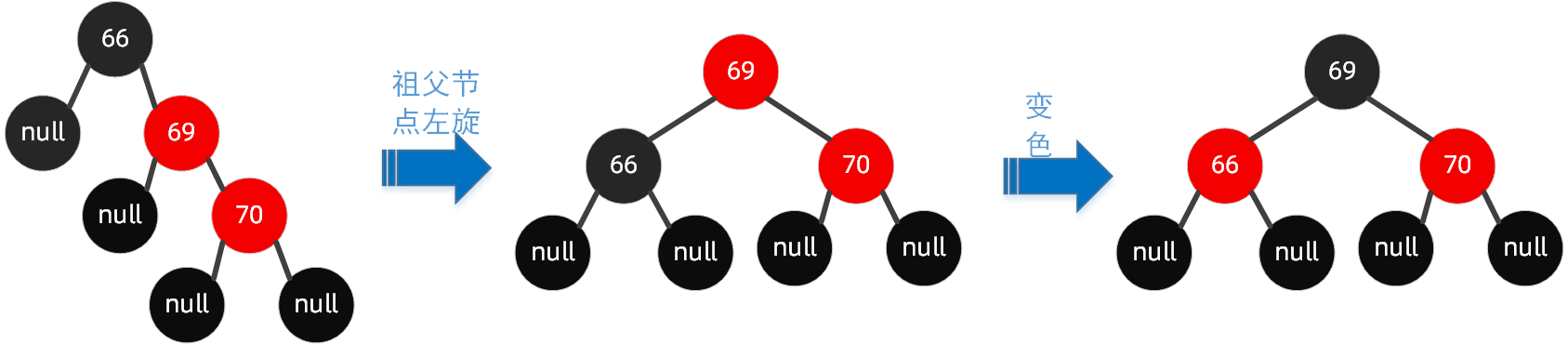
3.6 红黑树插入总结
| 无需调整 | 【变色】即可实现平衡 | 【旋转+变色】才可实现平衡 | |
|---|---|---|---|
| 情况1: | 当父节点为黑色时插入子节点 | 空树插入根节点,将根节点红色变为黑色 | 父节点为红色左节点,叔父节点为黑色,插入左子节点,那么通过【左左节点旋转】 |
| 情况2: | - | 父节点和叔父节点都为红色 | 父节点为红色左节点,叔父节点为黑色,插入右子节点,那么通过【左右节点旋转】 |
| 情况3: | - | - | 父节点为红色右节点,叔父节点为黑色,插入左子节点,那么通过【右左节点旋转】 |
| 情况4: | - | - | 父节点为红色右节点,叔父节点为黑色,插入右子节点,那么通过【右右节点旋转】 |
四. 红黑树节点删除
相比较于红黑树的节点插入,删除节点更为复杂,我们从子节点是否为null和红色为思考维度来讨论。
4.1 子节点至少有一个为null
当待删除的节点的子节点至少有一个为null节点时,删除了该节点后,将其有值的节点取代当前节点即可,若都为null,则将当前节点设置为null,当然如果违反规则了,则按需调整,如【变色】以及【旋转】。
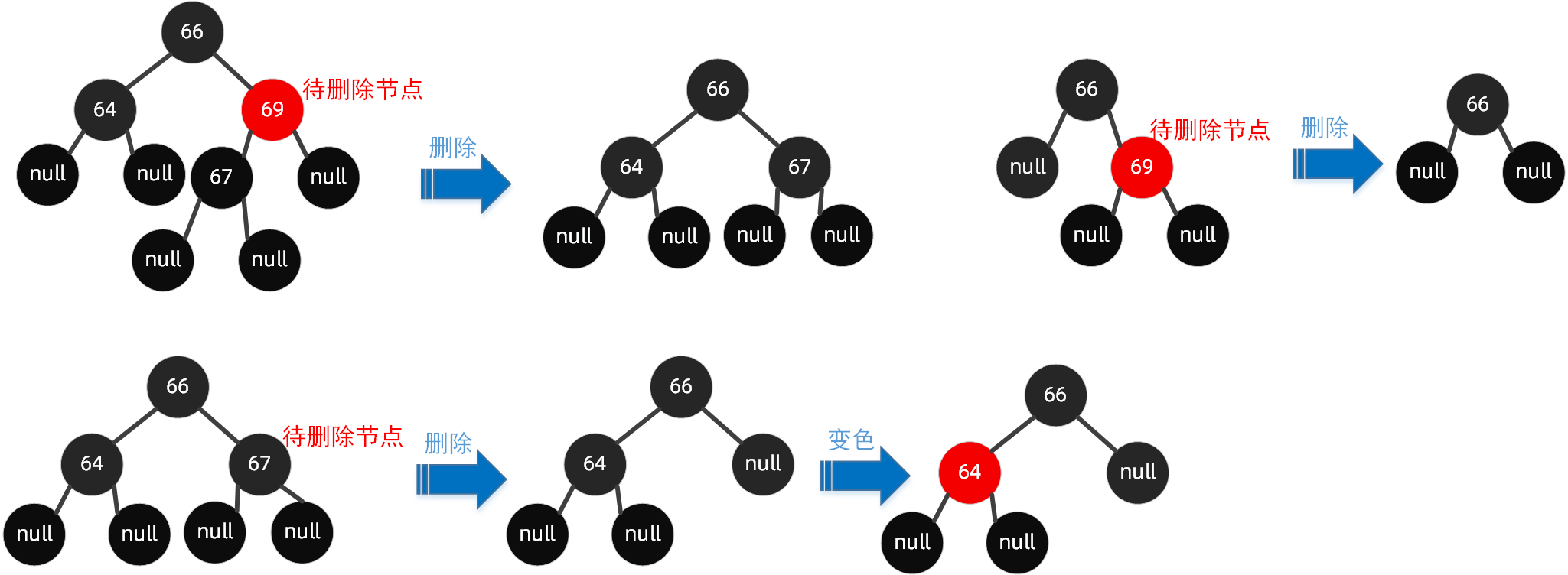
4.2 子节点都是非null节点
这种情况下,
第一步:找到该节点的前驱或者后继
前驱:左子树中值最大的节点(可得出其最多只有一个非null子节点,可能都为null);
后继:右子树中值最小的节点(可得出其最多只有一个非null子节点,可能都为null);
前驱和后继都是值最接近该节点值的节点,类似于该节点.prev = 前驱,该节点.next = 后继。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继;
这相当于是一种“取巧”的方法,我们删除节点的目的是使该节点的值在红黑树上不存在,因此专注于该目的,我们并不关注删除节点时是否真是我们想删除的那个节点,同时我们也不需考虑树结构的变化,因为树的结构本身就会因为自动平衡机制而经常进行调整。
前面我们已经说了,我们要删除的实际上是前驱或者后继,因此我们就以前驱为主线来讲解,后继的学习可参考前驱,包括几种情况
4.2.1 前驱为黑色节点,并且有一个非null子节点

分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则4,因此需要进行自动平衡调整;
这里直接通过【变色】即可完成。
4.2.2 前驱为黑色节点,同时子节点都为null
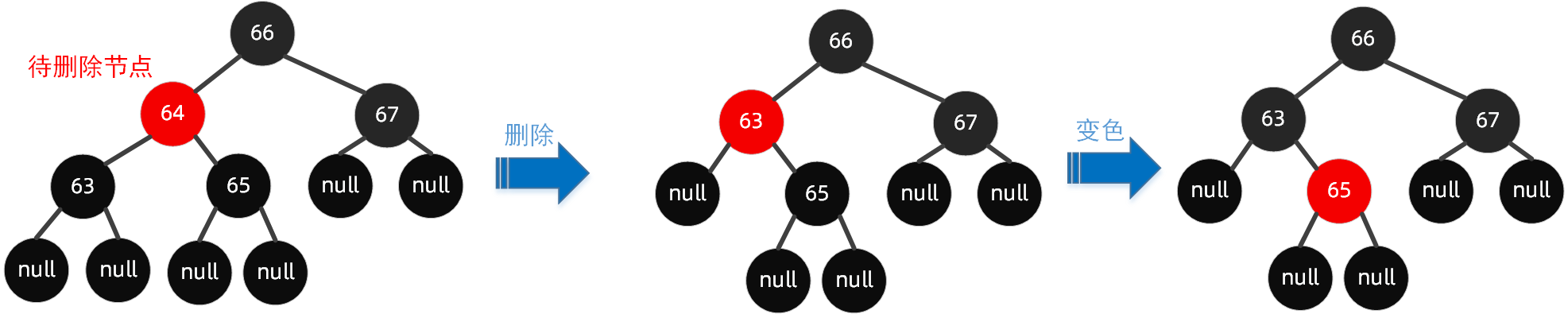
分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则5,因此需要进行自动平衡调整;
这里直接通过【变色】即可完成。
4.2.3 前驱为红色节点,同时子节点都为null

分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,树的结构并没有打破规则。
4.3 红黑树删除总结
红黑树删除的情况比较多,但也就存在以下情况:
删除的是根节点,则直接将根节点置为null;
待删除节点的左右子节点都为null,删除时将该节点置为null;
待删除节点的左右子节点有一个有值,则用有值的节点替换该节点即可;
待删除节点的左右子节点都不为null,则找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继;
节点删除后可能会造成红黑树的不平衡,这时我们需通过【变色】+【旋转】的方式来调整,使之平衡,上面也给出了例子,建议大家多多练习,而不必背下来。
五. 总结
本文主要介绍了红黑树的相关原理,首先红黑树的基础二叉搜索树,我们先简单说了一下二叉搜索树,并且讲了一下搜索的流程,然后就针对红黑树的6大规则特点,红黑树的插入操作,删除操作,都使用了大量的图形来加以说明,技术都是练出来的,有时候很多似是而非的地方,当动笔去写的时候,其实很好理解。红黑树的使用非常广泛,如TreeMap和TreeSet都是基于红黑树实现的,而Jdk8中HashMap当链表长度大于8时也会转化为红黑树,红黑树比较复杂,本人也是还在学习过程中,如果有不对的地方请批评指正,望共同进步谢谢。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号