bzoj4372 烁烁的游戏
题解:
动态 点分治。
点分治可以帮助我们将树上的点分层,如果我们把这些点按生成顺序建树的话,我们会得到一棵点分树。
点分树有一个特别好的性质,就是不管原来的树长什么样,建出来的点分树的深度都大约是$logn$。
而且若在点分树中a有一个儿子b,那么在原树中a的管辖子树(即找a作重心的子树)一定包含b的管辖子树。
(管辖子树这个名词是我瞎编的)
相当于把树分块,点分树中每一个点代表一块,
这样就是……树上线段树……了?
好像这就是动态点分。
本题要求区间修改,单点查询。
区间一个一个修改是不可能的,这辈子都不可能的
一定有骚操作,比如说挂几个标记。
比如每个点挂一棵线段树,然后记录管辖子树中和这个点距离为k的有多大收益。
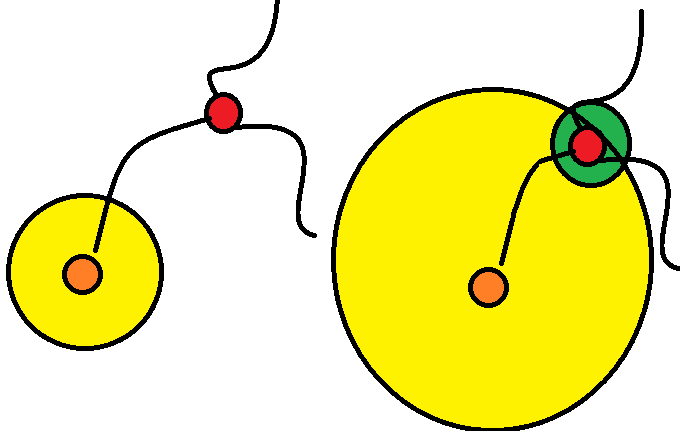
比如这个图。
红点是高级重心,橙点是低级重心。
我们会发现,橙点能力过强时,他可以将部分范围传给高级中心。
但是有重叠部分啊。

所以我们还需要再开一棵线段树。
由于一个低级中心在点分树中只能有一个高级中心做父亲,所以我们可以在低级中心记录溢出了多少。
这道题就愉快的结束了。
代码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define N 100050 inline int rd() { int f=1,c=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){c=10*c+ch-'0';ch=getchar();} return f*c; } int n,m,hed[N],cnt; char c; struct EG { int to,nxt; }e[2*N]; void ae(int f,int t) { e[++cnt].to = t; e[cnt].nxt = hed[f]; hed[f] = cnt; } int fa[N],son[N],dep[N],siz[N],top[N]; void dfs1(int u,int f) { fa[u] = f; siz[u] = 1; dep[u] = dep[f]+1; for(int j=hed[u];j;j=e[j].nxt) { int to = e[j].to; if(to==f)continue; dfs1(to,u); siz[u]+=siz[to]; if(siz[to]>siz[son[u]])son[u] = to; } } void dfs2(int u,int tp) { top[u] = tp; if(!son[u])return ; dfs2(son[u],tp); for(int j=hed[u];j;j=e[j].nxt) { int to = e[j].to; if(to!=fa[u]&&to!=son[u]) dfs2(to,to); } } int get_lca(int x,int y) { while(top[x]!=top[y]) { if(dep[top[x]]<dep[top[y]])swap(x,y); x = fa[top[x]]; } return dep[x]<dep[y]?x:y; } int get_dis(int x,int y) { return dep[x]+dep[y]-2*dep[get_lca(x,y)]; } int rt,mrk[N],uf[N],sum,w[N],sz[N]; void get_rt(int u,int f) { sz[u] = 1,w[u] = 0; for(int j=hed[u];j;j=e[j].nxt) { int to = e[j].to; if(to==f||mrk[to])continue; get_rt(to,u); sz[u]+=sz[to]; if(sz[to]>w[u])w[u]=sz[to]; } w[u] = max(w[u],sum - sz[u]); if(w[u]<w[rt])rt = u; } void work(int u) { mrk[u] = 1;int pre = sum; for(int j=hed[u];j;j=e[j].nxt) { int to = e[j].to; if(mrk[to])continue; rt = 0,sum = (sz[to]>sz[u]?pre-sz[u]:sz[to]); get_rt(to,0); uf[rt] = u; work(rt); } } struct segtree { int tot,rt[N],ls[150*N],rs[150*N],vl[150*N]; void insert(int l,int r,int &u,int qx,int d) { if(!u)u = ++tot; vl[u]+=d; if(l==r)return ; int mid = (l+r)>>1; if(qx<=mid)insert(l,mid,ls[u],qx,d); else insert(mid+1,r,rs[u],qx,d); } int query(int l,int r,int u,int ql,int qr) { if(!u)return 0; if(l==ql&&r==qr)return vl[u]; int mid = (l+r)>>1; if(qr<=mid)return query(l,mid,ls[u],ql,qr); else if(ql>mid)return query(mid+1,r,rs[u],ql,qr); else return query(l,mid,ls[u],ql,mid)+query(mid+1,r,rs[u],mid+1,qr); } void push(int x,int s,int d) { s = min(s,n); insert(0,n,rt[x],s,d); } int ask(int x,int s) { return query(0,n,rt[x],s,n); } }tr1,tr2; int main() { // freopen("1.in","r",stdin); n = rd(),m = rd(); for(int f,t,i=1;i<n;i++) { f = rd(),t = rd(); ae(f,t),ae(t,f); } dfs1(1,0),dfs2(1,1); w[0] = 0x3f3f3f3f,rt = 0,sum = n; get_rt(1,0); work(rt); for(int x,d,w,i=1;i<=m;i++) { c = getchar(); while(c!='Q'&&c!='M')c = getchar(); if(c=='Q') { x = rd(); int ans = 0,p=x; while(p) { ans+=tr1.ask(p,get_dis(p,x)); if(uf[p])ans-=tr2.ask(p,get_dis(uf[p],x)); p = uf[p]; } printf("%d\n",ans); }else { x = rd(),d = rd(),w = rd(); int p = x,las = 0; while(p) { int now = d-get_dis(p,x); if(now<0) { las = p,p = uf[p]; continue; } tr1.push(p,now,w); if(las)tr2.push(las,now,w); las = p,p = uf[p]; } } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号